哈夫曼树

前言

　　今天我们来研究一下哈夫曼树。这两天净鼓捣python,再不写写数据结构进度就跟不上了。

 

一些相关定义

　　路径：一个结点到另一个结点的分支序列

　　路径长度：一个结点到另一个结点所经过的分支数目

　　树的路径长度：根节点到每个结点的路径长度之和。

　　结点的权：赋予树的每个结点一带有实际意义的实数，该实数称为这个结点的权。

　　结点的带权路径长度：从根结点到该节点的路径长度与该结点权的乘积/。

　　树的带权路径长度：从根到每个叶子 的带权路径长度之和，通常记为

 

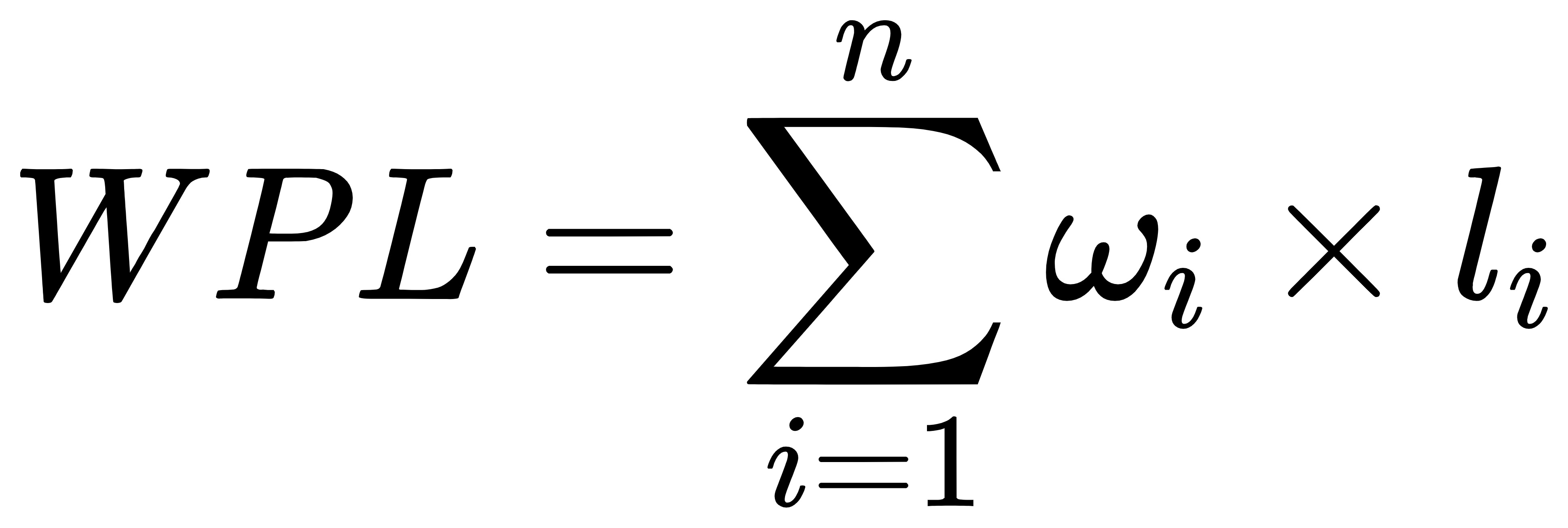
哈夫曼树

　　我们研究哈夫曼树的目的在于寻找最优。我们把由n个带权叶子结点构成的所以二叉树钟带权路径长度最短的二叉树叫做哈夫曼树。

　　那么什么样的二叉树最短呢？对于一个给定权值序列{2, 3, 4, 7}，我们给出三个例子：

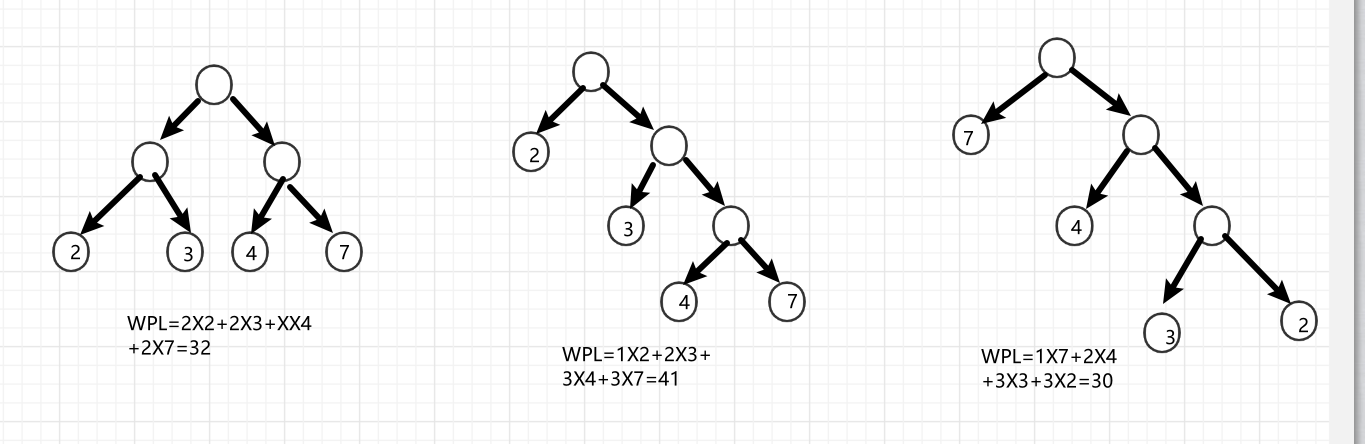
　　可以看出来，让权值大的结点靠近根，便可以构造一个最优二叉树，即哈夫曼树。

如何构造哈夫曼树？

1. ,初始化：用给定的n个权值 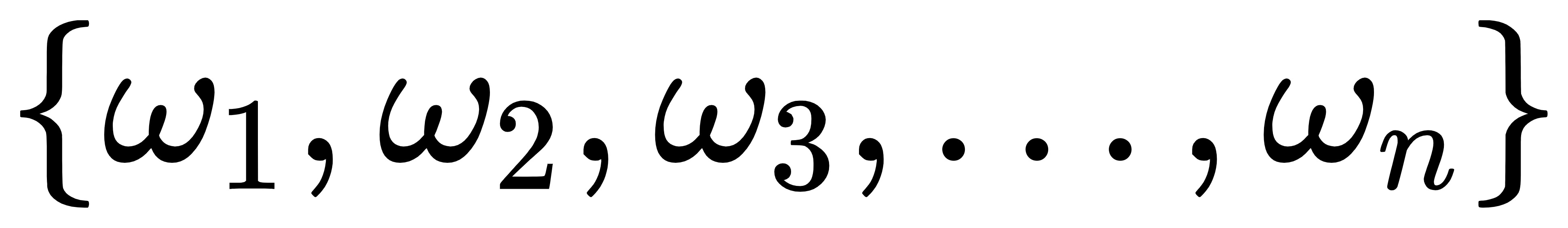构建n棵二叉树并构成森林$F = \left \{ {T}_{1},{T }_{2},{T }_{3},...,{T }_{n} \right \} $ 其中每一颗二叉树都仅有一颗权值为$\omega _{i} $的根结点，其左右子树为空。

2. 找最小树：在森林$F$中选择两颗根节点权值最小的二叉树，作为 一颗新二叉树的左右子树。标记新二叉树根节点权值为其左右子树的根节点权值之和。

3. 删除与加入：从$F$中删除被选中的那两颗二叉树，同时把新构成的二叉树加入森林$F$

4. 判断：重复②，③操作，直到森林中只含一颗二叉树，则该二叉树为哈夫曼树。 

代码实现 

存储结构

　　由于哈夫曼树中没有度为1的结点，故一颗有$n$个叶子的哈夫曼树共$2n-1$个结点，可以用大小为$2n-1$的一维数组来存储哈夫曼树，而每个结点还包含其双亲和孩子结点的信息，因此构成一个静态三叉链表。

类型定义

struct HuffmanTreeNode
{
    bool hasChecked;
    int weight;
    int LChild;
    int RChild;
    int parent;
};

const int N = 5;         //叶子结点的数目
const int M = 2 * N - 1; //共有M个结点

class HuffmanTree
{
public:
    HuffmanTreeNode tree[M + 1];
    void initHuffmanTree(int weight[], int n); //初始化函数
    void select(int max, int &s1, int &s2);    //选择在森林中、权值最小的两棵树
};

 

构建哈夫曼树

对于有$n$个结点的哈夫曼树，结点总数为$2n-1$个。我们知道这$n$个结点都是叶子结点，因此前$n$个位置存储叶子结点，后$n-1个存储其余结点。

void HuffmanTree::initHuffmanTree(int weight[], int n)
{
    //初始化前1~n个
    for (int i = 1; i <= n; i++)
    {
        tree[i] = {false, weight[i - 1], 0, 0, 0};
    }
    //初始化后n + 1~2n - 1个
    for (int i = n + 1; i <= 2 * n - 1; i++)
    {
        tree[i] = {false, 100, 0, 0, 0};
    }
    int s1, s2;
    for (int i = n + 1; i <= 2 * n - 1; i++)
    {
        select(i - 1, s1, s2);
        // 找出权值最小的两颗子树
        // 由于需要让权值小的在左子树，因此我们让权值s1 < s2
        tree[i].weight = tree[s1].weight + tree[s2].weight;
        tree[i].LChild = s1;
        tree[i].RChild = s2;

        tree[s1].parent = i;
        tree[s2].parent = i;
    }
}

选择树时我们需要用到之前定义的值hasChecked,当它为true时表示该数已经被检查不在森林内

void HuffmanTree::select(int max, int &s1, int &s2)
{
    //选择在森林中的两颗树
    int i, min = 999, k = 1;
    for (i = 1; i <= max; i++)
    {
        if (tree[i].hasChecked)     //不在森林就直接跳过
        {
            continue;
        }

        if (tree[i].weight < min)
        {
            min = tree[i].weight;
            k = i;
        }
    }
    s1 = k;
    tree[s1].hasChecked = true;     // 选择完这颗树后需把它移除森林，重新选择第二棵权值最小的树

    k = 1;
    min = 999;
    for (i = 1; i <= max; i++)
    {
        if (tree[i].hasChecked)
        {
            continue;
        }

        if (tree[i].weight < min)
        {
            min = tree[i].weight;
            k = i;
        }
    }
    s2 = k;
    tree[k].hasChecked = true;
}

至此，我们已经完整定义并创建了一颗哈夫曼树。

完整代码实现

/**
 * @file HuffmanTree.cpp
 * @author zh(帝皇の惊)(RickSchanze)
 * @brief 哈夫曼树
 * @date 2022-04-19
 */
#include <iostream>

struct HuffmanTreeNode
{
    bool hasChecked;
    int weight;
    int LChild;
    int RChild;
    int parent;
};

const int N = 5;         //叶子结点的数目
const int M = 2 * N - 1; //共有M个结点

class HuffmanTree
{
public:
    HuffmanTreeNode tree[M + 1];
    void initHuffmanTree(int weight[], int n); //初始化函数
    void select(int max, int &s1, int &s2);    //选择在森林中、权值最小的两棵树
};

void HuffmanTree::initHuffmanTree(int weight[], int n)
{
    //初始化前1~n个
    for (int i = 1; i <= n; i++)
    {
        tree[i] = {false, weight[i - 1], 0, 0, 0};
    }
    //初始化后n + 1~2n - 1个
    for (int i = n + 1; i <= 2 * n - 1; i++)
    {
        tree[i] = {false, 100, 0, 0, 0};
    }
    int s1, s2;
    for (int i = n + 1; i <= 2 * n - 1; i++)
    {
        select(i - 1, s1, s2);
        // 找出权值最小的两颗子树
        // 由于需要让权值小的在左子树，因此我们让权值s1 < s2
        tree[i].weight = tree[s1].weight + tree[s2].weight;
        tree[i].LChild = s1;
        tree[i].RChild = s2;

        tree[s1].parent = i;
        tree[s2].parent = i;
    }
}

void HuffmanTree::select(int max, int &s1, int &s2)
{
    //选择在森林中的两颗树
    int i, min = 999, k = 1;
    for (i = 1; i <= max; i++)
    {
        if (tree[i].hasChecked)     //不在森林就直接跳过
        {
            continue;
        }

        if (tree[i].weight < min)
        {
            min = tree[i].weight;
            k = i;
        }
    }
    s1 = k;
    tree[s1].hasChecked = true;     // 选择完这颗树后需把它移除森林，重新选择第二棵权值最小的树

    k = 1;
    min = 999;
    for (i = 1; i <= max; i++)
    {
        if (tree[i].hasChecked)
        {
            continue;
        }

        if (tree[i].weight < min)
        {
            min = tree[i].weight;
            k = i;
        }
    }
    s2 = k;
    tree[k].hasChecked = true;
}

int main()
{
    HuffmanTree aTree;
    int n;
    std::cin >> n;
    int weight[100];
    for (int i = 0; i < n; i++)
    {
        std::cin >> weight[i];
    }
    aTree.initHuffmanTree(weight, n);
    return 0;
}