建立二叉树的二叉链表【NOJ理论第18题】

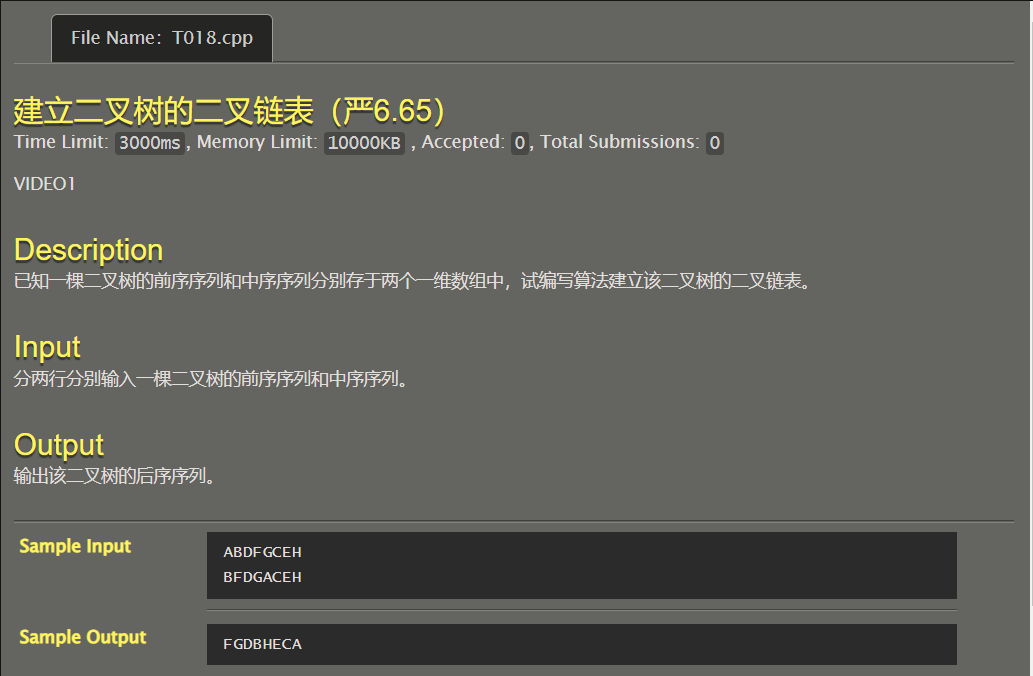
题目

思路

如果老老实实得遍历两个序列一个字母一个字母地读入并建立我认为实在是太麻烦。

因此我地核心思路是将这两个组合变为扩展地前序遍历序列，然后进行创建。

为此我们需要从前序序列开始遍历，并且要找到对应字母在中序的位置

int findAChar(char source, char *target)
{
    for (int i = 0; i < strlen(target); i++)
    {
        if (target[i] == source)
        {
            return i;
        }
    }
    return -1;
}

 将前序序列的第一个字母放入目标数组中，并在中序序列找到相应位置的，将那个位置置以一标志字符，表示我们处理过了。

        target[index] = *preOrder;　　　　//target为转化后的数组，index为转化后数组的下标，从0开始
        int trueindex = findAChar(*preOrder, inOrder);
        inOrder[trueindex] = '*';

若中序序列左边为'\0'或'*'表示子树为空，右边同理。

        if (inOrder[trueindex - 1] == '*' || inOrder[trueindex - 1] == '\0')
        {
            index++;
            target[index] = '#';
        }
        if (inOrder[trueindex + 1] == '\0' || inOrder[trueindex + 1] == '*')
        {
            index++;
            target[index] = '#';
        }
        index++;

同时需要时刻注意index的处理，这里不再赘述。

循环结束后新数组末尾置'\0'便得到了扩展前序遍历序列。剩下的不再赘述。

代码实现

#include <iostream>
#include <cstring>
using namespace std;
struct Node
{
    char data;
    Node *LChild;
    Node *RChild;
};

Node* createATree(char** s)
{
    if (**s == '#')
    {
        return nullptr;
    }
    Node* newNode = new Node;
    newNode->data = **s;
    (*s)++;
    newNode->LChild = createATree(s);
    (*s)++;
    newNode->RChild = createATree(s);
    return newNode;
}

int findAChar(char source, char *target)
{
    for (int i = 0; i < strlen(target); i++)
    {
        if (target[i] == source)
        {
            return i;
        }
    }
    return -1;
}
// 将前序遍历序列和中序遍历序列转换为扩展的前序遍历序列
void translate(char *preOrder, char *inOrder, char *target)
{
    // 符号*用于表示在中序遍历序列，该点的字符已经处理
    int index = 0;
    while (*preOrder != '\0' && *inOrder != '\0')
    {
        if (*preOrder == '*')
        {
            preOrder++;
            continue;
        }
        target[index] = *preOrder;
        int trueindex = findAChar(*preOrder, inOrder);
        inOrder[trueindex] = '*';
        if (inOrder[trueindex - 1] == '*' || inOrder[trueindex - 1] == '\0')
        {
            index++;
            target[index] = '#';
        }
        if (inOrder[trueindex + 1] == '\0' || inOrder[trueindex + 1] == '*')
        {
            index++;
            target[index] = '#';
        }
        index++;
        preOrder++;
    }
    target[index] = '\0';
}

void print(Node* aTree)
{
    if (aTree != nullptr)
    {
        print(aTree->LChild);
        print(aTree->RChild);
        cout << aTree->data;
    }
}

int main()
{
    char* preOrder = new char[100];
    preOrder[0] = '\0';
    char* inOrder = new char[100];
    inOrder[0] = '\0';
    char* target = new char[100];
    cin >> (preOrder + 1) >> (inOrder + 1);
    translate(preOrder + 1, inOrder + 1, target);
    Node* tree = createATree(&target);
    print(tree);
    return 0;
}