二叉树

前言

　　关于树是什么和一些术语我就不解释了，相信各位能用自己的力量找到

　　下面的内容大部分取自课本

介绍

　　二叉树的结构有如下特点：

每个结点的度都不能大于2
每个孩子结点次序不可颠倒

　　因此，对于二叉树的每一个结点而言，只有三种情况：

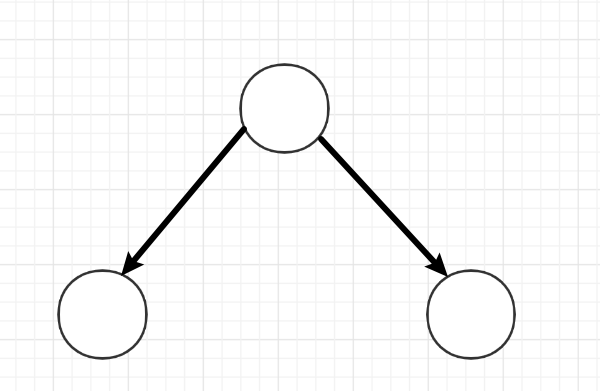
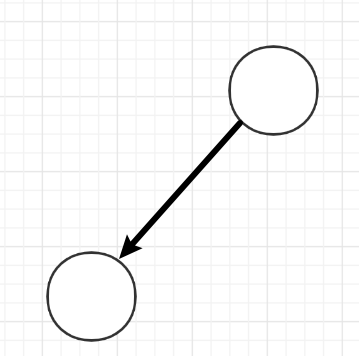
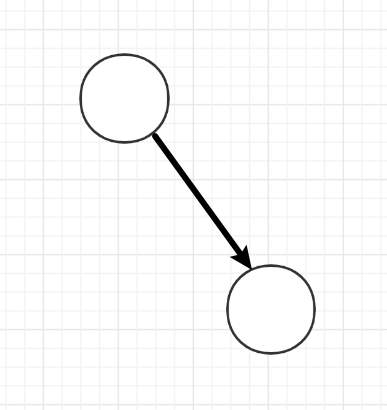
两种特殊的二叉树

满二叉树：在满二叉树中，每层结点都是满的，即每层结点都有最大节点数，如：

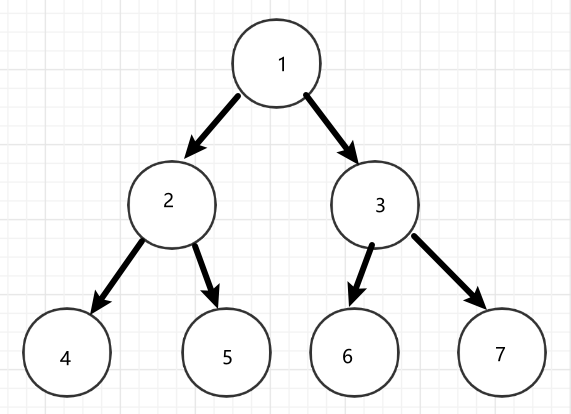
满二叉树的顺序表示：即从二叉树根开始，从上到下从左到右依次逐层进行编号

完全二叉树

对于深度为k，结点为n的二叉树，如果其结点1~n的位置序号与等高满二叉树1~n的位置序号一一对应，则为完全二叉树，如图

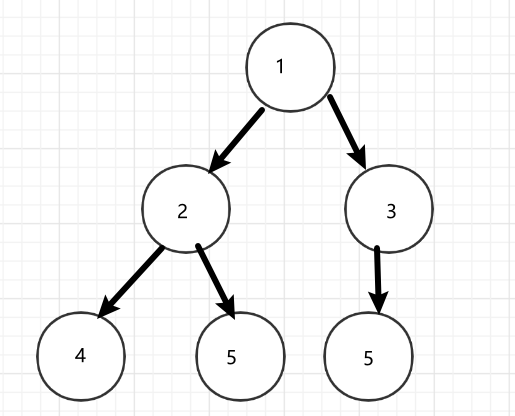
对于完全二叉树：

叶子结点只可能出现在最后层
度为1的结点个数为0或1

性质

二叉树的第 i 层上至多有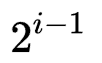个结点
深度为k的二叉树之多有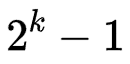个结点
对任意二叉树，若终端结点数为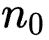,而其度数为2的结点数为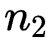,则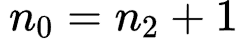
具有 n 个结点的完全二叉树的深度为
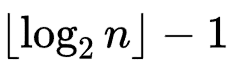
对于具有n个结点的完全二叉树，如果按从上到下，从左到右的顺序对二叉树中所有结点从1开始编号，则对于任意序号为i的结点有:

- 若 i = 1 ,则序号i的结点就是根节点，若 i > 1，则序号为 i 的结点的双亲结点序号为
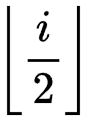
- 若 2i > n，则序号为i的结点无左孩子；若2i<=n,则序号为i的结点的左孩子结点序号为2i。
- 若2i+1>n,则序号为i的结点无有孩子，若2i+1<=n,则序号为i的结点的右孩子结点的序号为2i+1

注：符号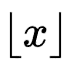指不大于 x 的最大整数

二叉树的存储结构

采用链式存储，因为顺序存储在某些情况下浪费太大。

二叉树单节点的结构：

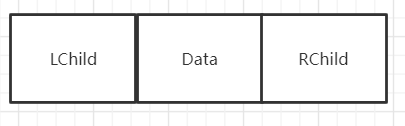
一个二叉链表的结构：

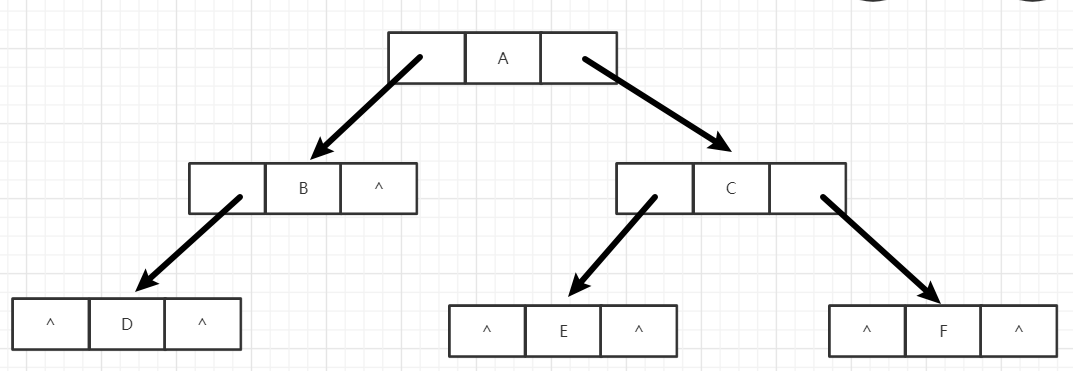
二叉树的遍历

因为课本上二叉树的建立用到了遍历里面的东西，因此先说二叉树的遍历

先序遍历

操作有三：

访问根节点
按先序遍历左子树
按先序遍历后字数

代码描述

void preOrder(BinaryTree root)
{
    if (root != nullptr)
    {
        visit(root->data);
        preOrder(root->LChild);
        preOrder(root->RChild);
    }
}

中序遍历

操作有三：

按中序遍历左子树
访问根节点
按中序遍历右子树

代码描述

void inOrder(BinaryTree root)
{
    if (root != nullptr)
    {
        inOrder(root->LChild);
        visit(root->data);
        inOrder(root->RChild);
    }
}

后序遍历

操作：

后序遍历左子树
后序遍历右子树
访问根节点

代码描述

void postOrder(BinaryTree root)
{
    if (root != nullptr)
    {
        postOrder(root->LChild);
        postOrder(root->RChild);
        visit(root->data);
    }
}

遍历算法的应用

1.建立二叉链表方式存储的二叉树

给定一颗二叉树的遍历序列，可以相应的创建二叉链表。这里所说的遍历序列是一种“扩展的遍历序列”，在扩展的遍历序列中，必须用特定元素表示空子树

例如：对于扩展的先序遍历序列

AB.DF..G..C.E.H..

其二叉树结构为：

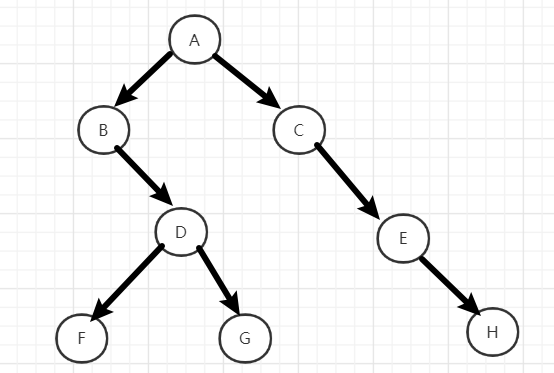
代码描述：

void createBinaryTree(BinaryTree* root)     //使用二重指针是为了能改变root的指向
{
    char ch;
    ch = cin.get();
    if (ch == '.')
    {
        *root = nullptr;
    }
    else
    {
         *root = new Node;
         (*root)->data = ch;
         createBinaryTree(&((*root)->LChild));      //因为是二重指针
         createBinaryTree(&((*root)->RChild));      //因为是二重指针
    }
}

2.先序遍历输出二叉树中结点

代码描述

void preOrderPrint(BinaryTree root)
{
    //先序遍历输出二叉树结点
    if (root != nullptr)
    {
        cout << root->data << " ";
        preOrder(root->LChild);
        preOrder(root->RChild);
    }
}

3.统计叶子结点数目

方法一：

int leafNum = 0;
void leafCount(BinaryTree root)
{
    if (root != NULL)
    {
        leafCount(root->LChild);
        leafCount(root->RChild);
        if (root->LChild == nullptr && root->RChild == nullptr)
        {
            leafNum++;
        }
    }
}

方法二：

int leafCount2(BinaryTree root)
{
    int leafCount = 0;
    if (root == NULL)
    {
        leafCount = 0;
    }
    else if (root->LChild == NULL && root->RChild == NULL)
    {
        leafCount = 1;
    }
    else
        leafCount = leafCount2(root->LChild) + leafCount2(root->RChild);
    return leafCount;
}

4.二叉树高度

方法一：分治法

int postTreeDepth(BinaryTree root)
{
    int hl, hr, max;
    if (root != NULL)
    {
        hl = postTreeDepth(root->LChild);
        hr = postTreeDepth(root->RChild);
        max = hl > hr ? hl : hr;
        return max + 1;
    }
    else
        return 0;
}

方法二：先序遍历

int depth = 0;
void preTreeDepth(BinaryTree root, int h)
{
    if (root != nullptr)
    {
        if (h > depth)
        {
            depth = h;
            preTreeDepth(root->LChild, h + 1);
            preTreeDepth(root->RChild, h + 1);
        }
    }
}

5.后续遍历的非递归算法

使用： std::stack

//后续遍历二叉树的非递归算法
void postOrderTree(BinaryTree root)
{
    Node *p, *q;
    stack<BinaryTree> aStack;
    q = nullptr;
    p = root;
    while (p != nullptr || !aStack.empty())
    {
        if (p != nullptr)
        {
            aStack.push(p);
            p = p->LChild;      //遍历左子树
        }
        else 
        {
            p = aStack.top();
            if (p->RChild == nullptr || p->RChild == q) //无右孩子或右孩子已遍历过
            {
                visit(p->data); //访问根结点
                q = p; //保存到q，作为下一次处理的前驱
                aStack.pop();
                p = nullptr;
            }
            else
                p = p->RChild;
        }
    }
}

完整测试代码

#include <iostream>
#include <stack>
using namespace std;
struct Node
{
    char data;
    Node *LChild = nullptr;
    Node *RChild = nullptr;
};

typedef Node *BinaryTree;

void visit(char a)
{
    cout << a << endl;
}
void preOrder(BinaryTree root)
{
    if (root != nullptr)
    {
        visit(root->data);
        preOrder(root->LChild);
        preOrder(root->RChild);
    }
}

void inOrder(BinaryTree root)
{
    if (root != nullptr)
    {
        inOrder(root->LChild);
        visit(root->data);
        inOrder(root->RChild);
    }
}

void postOrder(BinaryTree root)
{
    if (root != nullptr)
    {
        postOrder(root->LChild);
        postOrder(root->RChild);
        visit(root->data);
    }
}

void createBinaryTree(BinaryTree *root) //使用二重指针是为了能改变root的指向
{
    char ch;
    ch = cin.get();
    if (ch == '.')
    {
        *root = nullptr;
    }
    else
    {
        *root = new Node;
        (*root)->data = ch;
        createBinaryTree(&((*root)->LChild)); //因为是二重指针
        createBinaryTree(&((*root)->RChild)); //因为是二重指针
    }
}
//////////////////////////////////////////////////////////
void preOrderPrint(BinaryTree root)
{
    //先序遍历输出二叉树结点
    if (root != nullptr)
    {
        cout << root->data << " ";
        preOrder(root->LChild);
        preOrder(root->RChild);
    }
}

int leafNum = 0;
void leafCount(BinaryTree root)
{
    if (root != NULL)
    {
        leafCount(root->LChild);
        leafCount(root->RChild);
        if (root->LChild == nullptr && root->RChild == nullptr)
        {
            leafNum++;
        }
    }
}
// 2
int leafCount2(BinaryTree root)
{
    int leafCount = 0;
    if (root == NULL)
    {
        leafCount = 0;
    }
    else if (root->LChild == NULL && root->RChild == NULL)
    {
        leafCount = 1;
    }
    else
        leafCount = leafCount2(root->LChild) + leafCount2(root->RChild);
    return leafCount;
}

int postTreeDepth(BinaryTree root)
{
    int hl, hr, max;
    if (root != NULL)
    {
        hl = postTreeDepth(root->LChild);
        hr = postTreeDepth(root->RChild);
        max = hl > hr ? hl : hr;
        return max + 1;
    }
    else
        return 0;
}

int depth = 0;
void preTreeDepth(BinaryTree root, int h)
{
    if (root != nullptr)
    {
        if (h > depth)
        {
            depth = h;
            preTreeDepth(root->LChild, h + 1);
            preTreeDepth(root->RChild, h + 1);
        }
    }
}

//后续遍历二叉树的非递归算法
void postOrderTree(BinaryTree root)
{
    Node *p, *q;
    stack<BinaryTree> aStack;
    q = nullptr;
    p = root;
    while (p != nullptr || !aStack.empty())
    {
        if (p != nullptr)
        {
            aStack.push(p);
            p = p->LChild;      //遍历左子树
        }
        else 
        {
            p = aStack.top();
            if (p->RChild == nullptr || p->RChild == q) //无右孩子或右孩子已遍历过
            {
                visit(p->data); //访问根结点
                q = p; //保存到q，作为下一次处理的前驱
                aStack.pop();
                p = nullptr;
            }
            else
                p = p->RChild;
        }
    }
}
int main()
{
    BinaryTree aTree;
    createBinaryTree(&aTree);
    postOrderTree(aTree);
    cout << endl;
    postOrder(aTree);
    cout << endl;
    preOrderPrint(aTree);
    cout << endl;
    leafCount(aTree);
    cout << leafNum << endl;
    cout << leafCount2(aTree) << endl;
    cout << postTreeDepth(aTree) << endl;
    preTreeDepth(aTree, 1);
    cout << depth << endl;
}

posted @ 2022-04-01 19:16 帝皇の惊阅读(175) 评论(0) 收藏举报

刷新页面返回顶部

RickSchanze

二叉树

前言

介绍

两种特殊的二叉树

性质

二叉树的存储结构

二叉树的遍历

先序遍历

中序遍历

后序遍历

遍历算法的应用

1.建立二叉链表方式存储的二叉树

2.先序遍历输出二叉树中结点

3.统计叶子结点数目

4.二叉树高度

5.后续遍历的非递归算法

完整测试代码

公告