以三元组为存储结构实现矩阵相加（NOJ理论第12题）

前言

　　其实这题就是一大堆if else而已

题目描述

 

 

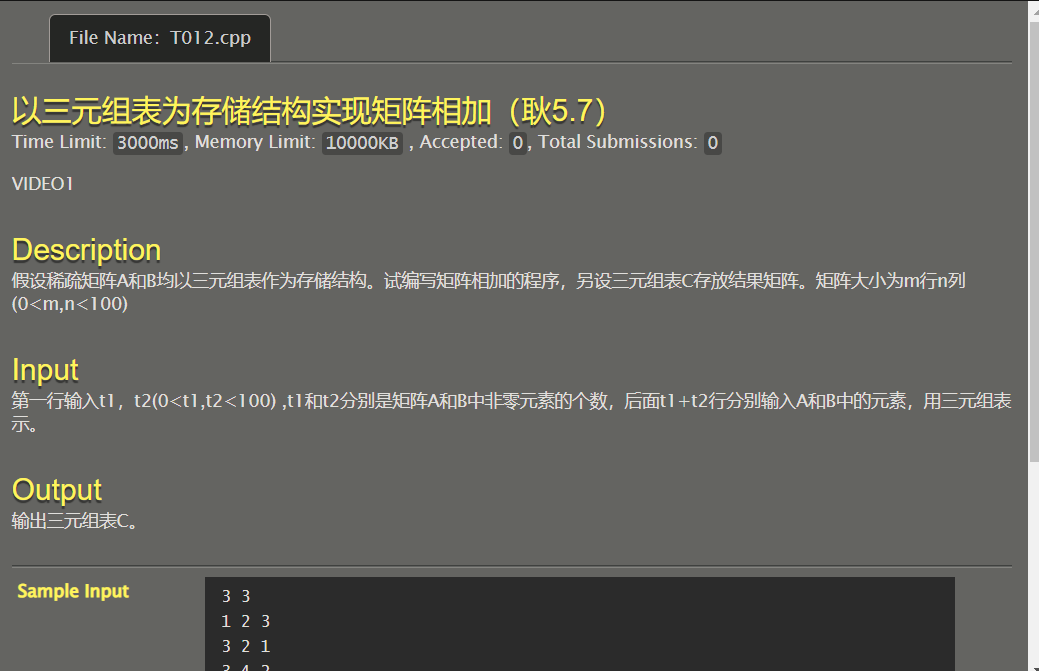
解题思路

我们解题时得考虑以下问题：

1. 如何保证有序？
2. 如何保证不重复？
3. 如果相加后为0了怎么办？

这三个问题解决了，这道题也就解决了。

对此我的解决思路为：

• 如何保证有序？

　　　　按给得三元组表从上到下依次进行相加。

• 如何保证不重复？

　　　　使用辅助变量，哪个表元素入C就把哪个表索引加一。

• 如果相加为0了这么办？

　　　　跳过该元素

细节都在注释里了

实现

//以三元组为存储结构实现矩阵相加
#include <iostream>

using namespace std;

struct Tuple
{
    int row;
    int col;
    int value;
};

void go_on(Tuple *aTuple, Tuple *C, int *Cin, int now, int len) //这个函数用来解决一个三元组表已全部入C
{                                                               //而另一三元组表还未到顶的问题
    for (int i = now; i < len; i++)
    {
        C[*Cin] = aTuple[i];
        (*Cin)++;
    }
}

int main()
{
    int AL, BL;
    cin >> AL >> BL;
    Tuple *martixA = new Tuple[AL],
          *martixB = new Tuple[BL],
          *martixC = new Tuple[AL + BL]; //为各三元组表分配足够大的空间
    for (int i = 0; i < AL; i++)
    {
        cin >> martixA[i].row >> martixA[i].col >> martixA[i].value;
        cin.get();
    }
    for (int i = 0; i < BL; i++)
    {
        cin >> martixB[i].row >> martixB[i].col >> martixB[i].value;
        cin.get();
    }

    //开始计算
    int countA = 0, countB = 0, countC = 0;
    //上面三个数各自代表遍历时达到的位置
    while (countA < AL && countB < BL)
    {
        if (martixA[countA].row == martixB[countB].row) //首先比较行
        {
            if (martixA[countA].col == martixB[countB].col) //然后是列
            {
                martixC[countC].row = martixA[countA].row;
                martixC[countC].col = martixA[countA].col;
                int temp = martixA[countA].value + martixB[countB].value;
                countA++;
                countB++;
                if (!temp)
                {
                    continue;
                }
                else
                {
                    martixC[countC].value = temp;
                }
            }
            else if (martixA[countA].col < martixB[countB].col)
            {
                martixC[countC] = martixA[countA];
                countA++;
            }
            else
            {
                martixC[countC] = martixB[countB];
                countB++;
            }
        } //如果行不相等就不用想了，让行小的那一个入C就行了
        else if (martixA[countA].row < martixB[countB].row)
        {
            martixC[countC] = martixA[countA];
            countA++;
        }
        else
        {
            martixC[countC] = martixB[countB];
            countB++;
        }
        countC++;
    }
    if (countA == AL)
    {
        go_on(martixB, martixC, &countC, countB, BL);
    }
    else if (countB == BL)
    {
        go_on(martixA, martixC, &countC, countA, AL);
    }
    //遍历
    for (int i = 0; i < countC; i++)
    {
        cout << martixC[i].row << " " << martixC[i].col << " " << martixC[i].value << endl;
    }
}