稀疏矩阵

稀疏矩阵是指大多数元素为0的矩阵，假设一个矩阵具有的行列数分别为m,n;非零项为t，则矩阵的稀疏因子 δ 为

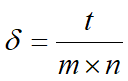
当 δ <= 0.05时，我们认为该矩阵为稀疏矩阵。

稀疏矩阵的三元组表表示法

只存储非零元素，使用三元组的结构存储，即：

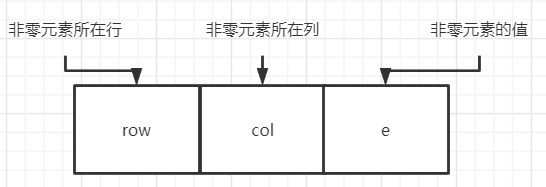
由此我们可以得到矩阵的三元组表，同时为了方便处理，在三元组表中，行号为主序并递增放置，如：

下标	行号	列号	元素值
1	1	2	12
2	1	3	9
3	3	1	-3
4	3	6	14
5	4	3	24
6	5	2	18
7	6	1	15
8	6	4	-7

上三元组表组成矩阵

现仅对三元组稀疏矩阵进行类型定义

#define MAXSIZE 1000
#define ElementType int
struct Tuple
{
    int row;
    int col;
    ElementType element;
};

struct SparseMatrix
{
    Tuple data[MAXSIZE + 1]; //非零元素的三元组表，data[0]未使用
    int m;                   //行数
    int n;                   //列数
    int len;                 //非零元个数
};

有关计算将在题解中给出

稀疏矩阵的链式存储结构：十字链表

当需要进行矩阵加法、乘法、减法运算时，矩阵中的非零元素的个数和位置可能发生巨大的变化，这时势必会为了保存“以行序为主序”而大量移动元素，因此使用十字链表来存储

在十字链表中，矩阵每一个非零元素用一个结点表示。同时还需要添加两个链域：

• right用于链接同一行的下一个非零元素
• down用于链接同一列的下一个非零元素

如下图是一个结点的结构

 

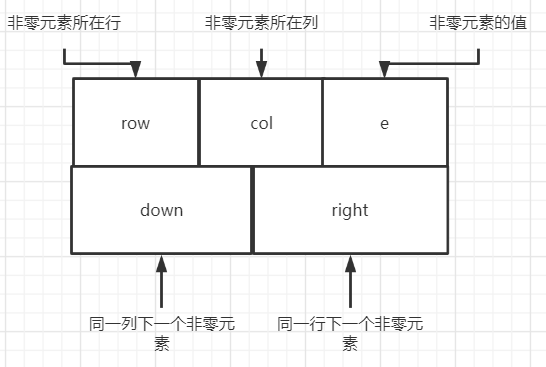
 例如，对于矩阵：

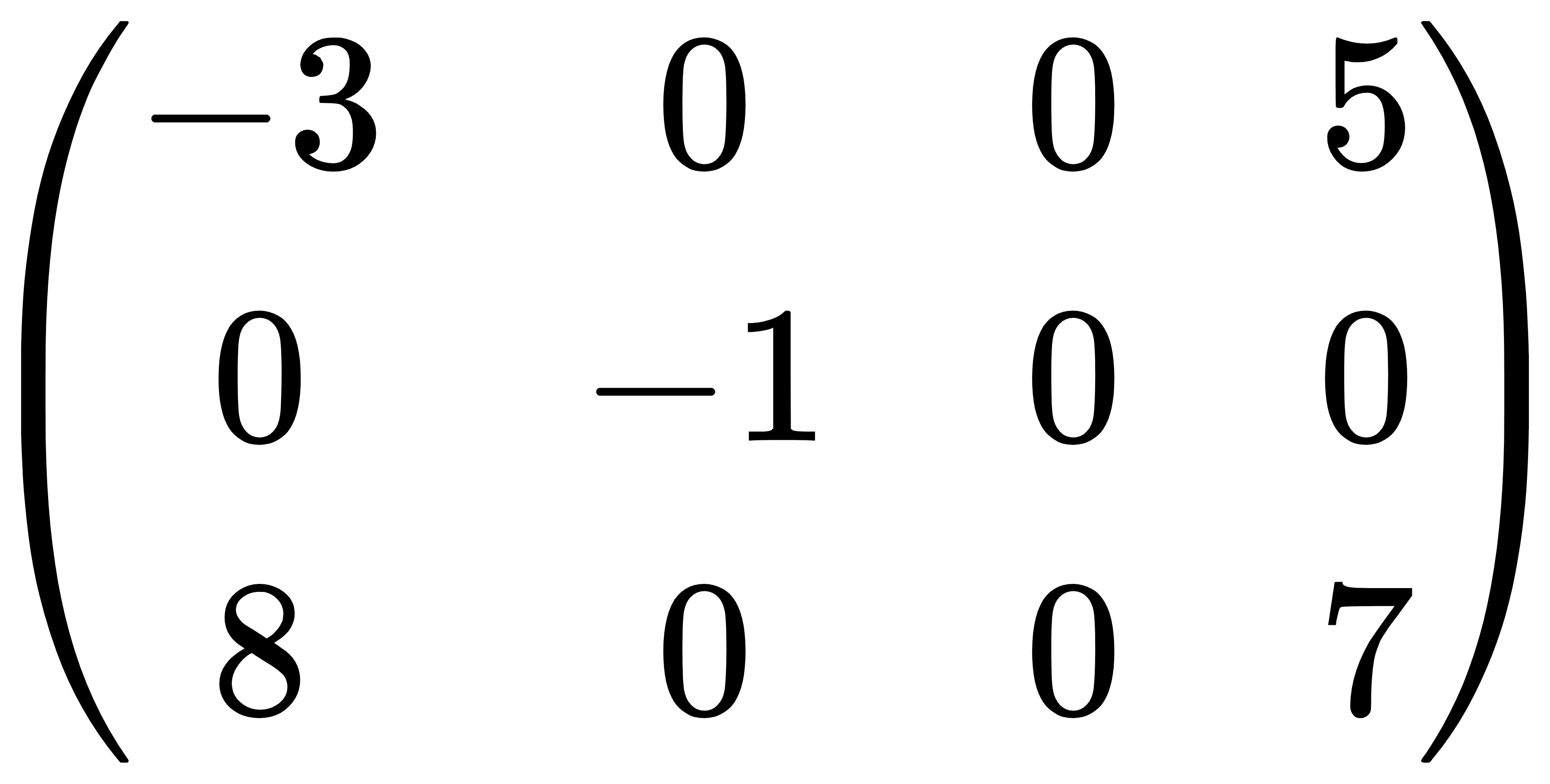
其十字链表表示为：

 

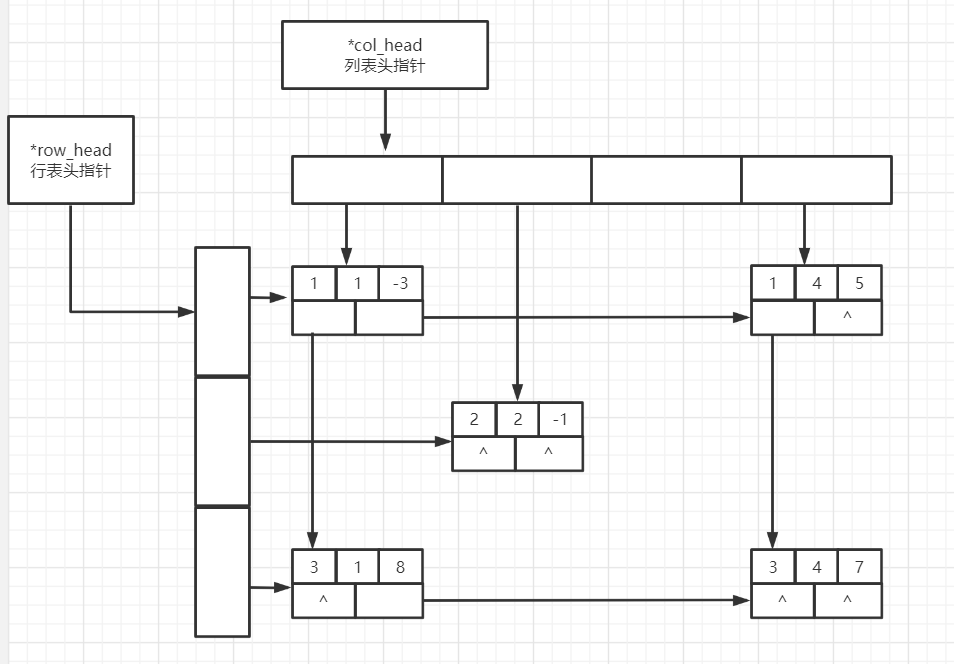
十字链表的实现

• 十字链表的结构类型定义

#include <iostream>
#define ElementType int
struct OLNode
{
    int row;              //行
    int col;              //列
    ElementType value;    //值
    OLNode *right, *down; //非零元素所在行表、列表的后继链域
};

typedef OLNode *OLink;

struct CorssList
{
    OLink *row_head, *col_head; //行、列链表头指针向量
    int m;                      //行数
    int n;                      //列数
    int len;                    //非零元个数
};

• 十字链表的建立

　　步骤：

1. 读入稀疏矩阵的行数、列数、非零元个数
2. 动态申请行链表的头指针向量、列链表的头指针向量
3. 逐个读入非零元素，分别插入行链表、列链表

 　　实现示例：

void CrossList::CreateCorssList(CrossList *aList)
{
    // 1.读入行数列数非零元个数
    int m, n, l, rowIn, colIn, elementIn;
    std::cin >> m >> n >> l;
    aList->rowNum = m;
    aList->colNum = n;
    aList->len = l;
    // 2.动态申请行链表头指针向量和列链表头指针向量
    aList->row_head = (OLink *)malloc((m + 1) * sizeof(OLink));
    aList->col_head = (OLink *)malloc((n + 1) * sizeof(OLink));
    if (!(aList->row_head && aList->col_head))
    { //其中一个没有申请成功
        std::cout << "overflow";
        return;
    }
    //初始化行列向量，令其每一项都为空
    for (int i = 0; i < m + 1; i++)
    {
        aList->row_head[i] = NULL;
    }
    for (int i = 0; i < n + 1; i++)
    {
        aList->col_head[i] = NULL;
    }

    // 3.开始插入
    while (1)
    {
        std::cin >> rowIn >> colIn >> elementIn;
        if (rowIn == 0)
        {
            break;
        }
        OLNode *newNode = (OLNode *)malloc(sizeof(OLNode));
        if (!newNode)
        {
            std::cout << "overflow";
            return;
        }

        newNode->row = rowIn;
        newNode->col = colIn;
        newNode->value = elementIn;
        newNode->right = NULL;
        newNode->down = NULL;

        //处理行
        if (aList->row_head[rowIn] == NULL)
        {
            aList->row_head[rowIn] = newNode;
        }
        else if (newNode->col < aList->row_head[rowIn]->col)
        {
            //新建结点列号 < 该行首个结点的列号，则插到结点开头
            newNode->right = aList->row_head[rowIn];
            aList->row_head[rowIn] = newNode;
        }
        else
        {
            //新建结点列号 > 改行首个结点的列号
            //寻找行表中的插入位置
            OLNode *q;
            for (q = aList->row_head[rowIn]; q->right && q->right->col < colIn; q = q->right)
                ;//空语句，因为这个for只是为了寻找合适插入位置而已
            newNode->right = q->right;
            q->right = newNode;
        }

        //处理列
        if (aList->col_head[colIn] == NULL)
        {
            aList->col_head[colIn] = newNode;
        }
        else if (newNode->row < aList->col_head[colIn]->row)
        {
            newNode->down = aList->col_head[colIn];
            aList->col_head[colIn] = newNode;
        }
        else
        {
            OLNode *q;
            for (q = aList->col_head[colIn]; q->down && q->down->row < rowIn; q = q->down)
                ;
            newNode->down = q->down;
            q->down = newNode;
        }
    }
}

 插入过程我理解了好一会，总结来说就是：

• 输入行row、列col、数
• 明确col_head与row_head其实都是数组
• 看row_head的第row个元素（相当于第row行的首元素）是不是空，如果是空，直接将新建元素插入
• 如不不是空，且小于row_head第row个元素的列数(col),则在该元素之前插入，并让新结点right指向row_head的第row个元素（首元素）
• 如果大于首元素，则应该向后插，利用for循环寻找合适插入位置，进行插入
• 对col_head的处理与上面相同

结尾吐槽

　　十字链表算是这学期学数据结构以来最复杂的结构了。这篇文章是从课本来的，所以使用了二重指针表示数组，不过这样做的缺点是不能通过vscode调试器来直观查看内存了

　　另外，我特别想吐槽课本上的写代码方式：为什么要用连写？你觉得这样很酷吗？啊？