逆波兰式（NOJ第8题）

前言

　　对于NOJ，其实我最想吐槽的就是没有测试点输入输出的数据，这样我们只能拿前辈的代码来进行测试。

　　就像这道题，我一开始全用的栈（因为课本上那道表达式的题用的就是栈），结果搁那耗了将近三个小时才想到合适的数据结构。

　　而且我在解题的过程中，发现编程题好像就是在让我们钻研数学的本质。让我们在种种限制下起舞。

　　还是太菜了啊。

 

题目描述

 

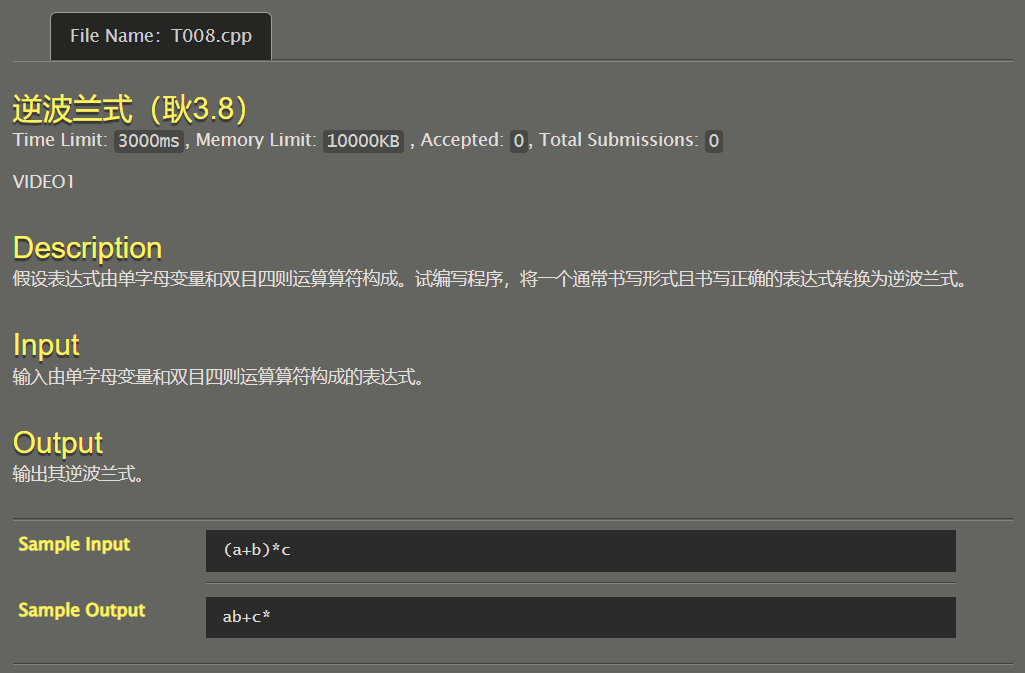
 这道题我真感觉坑挺大的，因为这道题要求字母顺序不变，认不清这点，就会白花好长时间（应该不是我自己）。

我们先来看逆波兰式的例子吧

　　(a+b)∗(c+d)    ⟶    ab+cd+∗　　

(a+(b+c))    ⟶    abc++

(1+2)∗3/4∗(7+8)    ⟶    12+3∗4/78+∗

基本就是以上的形式，愿君看清再做题。

算法设计

　　在这道题中，我们会遇到六个符号

( ) + - * /

　为了保证数字能按照顺序输出，我们使用队列来存储输入数据和其中的运算数

　   为了能让操作符正确的输出（按照（）、【*、/】、【+、-】）来输出，我们使用栈来保存操作符

　　而我们又考察到无论什么运算符，左边的都可以优先计算，所以我们从左边开始。

　　　　1.循环地从输入队列（SQ）中取出单个字符

　　　2.①如果是操作数，则入操作数队列（NQ）

　　　　②如果是操作符，则：

　　　　　　（1）如果是'('，则入操作符栈（OS)

　　　　　　（2）如果是')',  则：

　　　　　　　　　　Ⅰ.让NQ中所有数依次出队并输出

　　　　　　　　　　Ⅱ.让OS中所有除'('外地操作符出栈并输出

　　　　　　（3）如果是'*'或'/'，则：

　　　　　　　　　　Ⅰ.如果下一操作符是'(',则直接让下一操作符入栈

　　　　　　　　　　Ⅱ.如果不是，则先SQ出队并输出，然后OS出栈并输出

　　　　　　  (4)  如果是'+'或'-'，则入OS栈

　　　　　　（5）如果是操作数，则如NQ队列

　　上述操作完成后，可以保证所有工作地正确地做完。

实现

//逆波兰式
#include <iostream>
#include <cstring>
using namespace std;

struct Queue
{
    char queue[100];
    int rear = 0;
    int front = 0;
    char pop()
    {
        char rtn = queue[front];
        front++;
        return rtn;
    }
    char getTop()
    {
        return queue[front];
    }
    void push(char x)
    {
        queue[rear] = x;
        rear++;
    }
    bool isEmpty()
    {
        return front >= rear;
    }
};

struct Stack
{
    char stack[100];
    int top = -1;
    char pop()
    {
        char rtn = stack[top];
        top--;
        return rtn;
    }
    char getTop()
    {
        return stack[top];
    }
    void push(char x)
    {
        top++;
        stack[top] = x;
    }
    bool isEmpty()
    {
        return top == -1;
    }
};

bool isNormalOperator(char x)
{
    if (x == '+' || x == '-')
    {
        return true;
    }
    return false;
}

bool isGreaterOperator(char x)
{
    if (x == '*' || x == '/')
    {
        return true;
    }
    return false;
}

bool isLeftBracket(char x)
{
    if (x == '(')
    {
        return true;
    }
    return false;
}

bool isRightBracket(char x)
{
    if (x == ')')
    {
        return true;
    }
    return false;
}

int main()
{
    Queue SQ;
    std::cin >> SQ.queue;
    SQ.rear = strlen(SQ.queue);
    Stack OS;
    Queue NQ;
    while (!SQ.isEmpty())
    {
        if (isLeftBracket(SQ.getTop()))
        {
            OS.push(SQ.pop());
        }
        else if (isRightBracket(SQ.getTop()))
        {
            char x = SQ.pop();
            while (!NQ.isEmpty())
            {
                std::cout << NQ.pop();
            }
            while (!OS.isEmpty())
            {
                if (isLeftBracket(OS.getTop()) || isRightBracket(OS.getTop()))
                {
                    OS.pop();
                }
                else
                {
                    std::cout << OS.pop();
                }
            }
        }
        else if (isGreaterOperator(SQ.getTop()))
        {
            OS.push(SQ.pop());
            char x = SQ.getTop();
            if (!isLeftBracket(x))
            {
                std::cout << SQ.pop();
                std::cout << OS.pop();
            }
            else
            {
                OS.push(SQ.pop());
            }
        }
        else if (isNormalOperator(SQ.getTop()))
        {
            OS.push(SQ.pop());
        }
        else
        {
            NQ.push(SQ.pop());
        }
    }
}

　　最前面的就是对栈和队列的实现，使用C函数可以很容易地实现那些类函数。

　　我已经把完整的伪代码写在上面了，相信不用再写注释了。

'