山东集训

DAY 1

模拟赛 T1：

看成维护颜色，时间二元组。

颜色好做，时间相当于一段相同颜色后缀的第一个，转为求从后往前第一个颜色不同的时间之后第一个，这个是个 3-side 求 \(\min\)。

从后往前第一个颜色不同的时间可以直接线段树维护颜色不同的最大次大值即可。

复杂度是高贵的单 \(\log\)。

模拟赛 T2：

• 做法一：

  直接做区间加，区间 \(=k\) 计数，平衡复杂度得到 \(n^{1.75}\) 做法。

  经过逐块处理可以大力优化数组寻址，直接通过。

  目前该方法获得了最优解。

• 做法二：

  考虑每个点若对答案有贡献，至少经过 \(m\) 次操作后，这个点不同于当前点的值才会对答案有贡献，否则只能是当前值贡献。

  换句话说，如果我们每 \(\le m-1\) 次统计一次答案，这个点对于不同的有贡献的 \(m\) 个数是 \(O(1)\) 的，也就是相当于只有第一个大于等于/小于等于当前值的 \(k \times m\) 。

  直接操作分块，然后块间离散化后暴力。最后求贡献直接枚举所有 \(i \in [1,n]\) 求就行了。

  为了保证复杂度，取块长为 \(\sqrt n\) 即可，复杂度 \(n^{1.5}\)。

模拟赛 T3

最大值的一个常见套路为枚举最大值，然后染色未被染色的部分。

按 \(x\) 分块，散块部分很难搞，我们把在散块里面的 所有边界拿出来 做离散化。但是不管完整跨过这个块的边界。

所有块会形成 \(n \sqrt log n\) 个矩形，因为一个矩形提供至多 4 个上下边界，和所在块的 \(\sqrt n\) 个竖边界拼成矩形。

现在我们有两种操作：散块完整矩形 +，整块一个区间的行 +（可能拆开边界）

先考虑如何求答案，和上面一样，我们相当于要求：散块完整矩形的矩形和，整块一个区间的行的和。

我们对于所有散块求出被染色后的和，然后做二维前缀和即可。

第二种我们把列拍扁，算出每一行被加的和，做一维前缀和即可。

我们需要维护这个两个前缀和前的数组。

由于染色是可以均摊的，我们直接对每个块开并查集，每一行开并查集，这样势能是正确的。

现在只需要考虑染色一个完整的矩形块，染色一整行所产生的贡献。

• 完整矩形块：

  • 维护矩形块：
    直接求出来这个矩形块在行上还有几行没被染色，剩下的部分都会被染成当前颜色，直接求出来面积即可。
  • 维护行：
    相当于对于一个区间的行，如果还未被染色，则加上当前矩形块在 \(x\) 方向上的宽度 \(d\) 乘染的颜色 \(c\)。这个打 tag 实现，记录 \(b_i\) 表示这个 tag 的和，每次相当于做 \(b_i+=[a_i=0] \times c \times d\)，然后在某一行被染色的时候计算。

• 一行：

  • 维护行：
    求出在这一行上还有几个矩形块未被染色以及他们的宽度之和，加上即可。
  • 维护矩形块：
    和上面的操作一样，仍然是形如 \(+=[a_i=0] \times c\) 的形式。

是人写的？

CF1814F Communication Towers

首先这个时间区间存在的东西一般只能使用线段树分治。

然后就只能用可撤销并查集了，我们可以把这东西看成动态树，有合并和分裂操作。

最后递归到分治树叶子的时候，我们要对 \(1\) 所在的并查集树打标记。

然后我们需要在分裂的时候下放标记。

但是需要细致维护，可以维护时间戳表示。

也可以简单的，每次接上的时候剪掉根的 tag。分裂的时候加上根的 tag。

P12462 [Ynoi Easy Round 2018] 星野爱久爱海

先考虑 \(q=1\)，先考虑必选根。

这个是个经典贪心，每次取最长根链，然后取反，如此往复。

最终相当于取带权长剖后前 k 大。

如果不必选根，我们发现若 \(k>1\)，则直径必选，因此可以以直径做根求。

对于 \(q\not=1\)，我们可以考虑上线段树。

这样直接做复杂度是 \(\frac{n}{k} \times k \log n+q\times k \log n\)。

注意到没有修改，可以使用静态数据结构，因此第层按 \(k\) 分块，然后建立 ST 表可以做到 \(n\log n+qk\)。

P6580 [Ynoi2019] 美好的每一天~ 不连续的存在

势能莫队。

直接莫队做启发式合并是错的，因为这样会导致一个大的点被一直加加加。

然后不太懂，之后再研究？

未公开题目：

经典每种颜色单独做，建立虚树。

然后相当于求保留 \([l,r]\) 内的边之后，虚树上至少包含一个实点的连通块个数。

如果只求联通块个数，可以点-边容斥，减掉的边的限制相当于 \((l,r)\) 在一个 2-side 矩形内部，可以二维数点。

之后需要进一步扣掉完全是虚点的联通块个数。

考虑找代表元，一个虚点能成为联通块的最高点，首先父亲边不能连。其次到所有不同子树的第一个实点儿子的边不能连。

不能连一条边的限制有点烦，相当于二维平面扣掉一个 2-side 矩形，并起来回出现阶梯状，只能拆分成阶梯个数个矩形。

但是注意到，在往上走的过程中，所有儿子的限制都会和父亲边的限制做合并。

我们拆成多少个阶梯个数，这些在合并的时候就会被父亲边合并（补图），他们会被推到上面，然后 min 相同的只用保留 max 最小的，同理 max 相同的只需要保留 min 最大的，因此产生了几个矩形，就会删掉几个点，所以是对的。

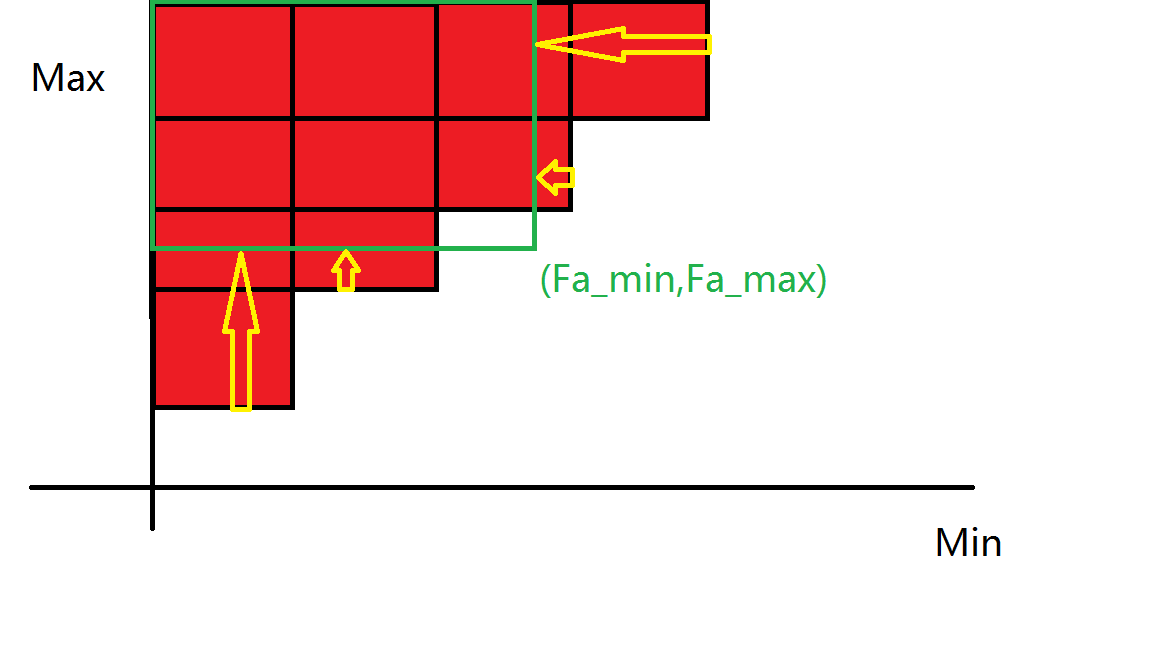
注意阶梯内部的是永远没有用了，因此只需要维护阶梯，这个写个线段树合并，以 min 为下标，维护 max 即可。

或者图省事可以直接维护 map。

PKUSC 2023 Day 2 A. 排队

可以看成每次加入一个偏序关系，撤销一个偏序关系，然后没有偏序关系之间的部分按照建立偏序关系的时间从大到小排序。

把偏序关系看成边，是一颗树。

相当于我们要维护动态树，每次删边加边维护 dfs 序列。

考虑直接拿平衡树维护会出现什么问题：不知道子树大小。

不过我们注意到一个事是，因为每次都会把子树接到一个节点上，然后作为第一个儿子，所以所有一个点所有儿子是按照从小到大排序的，和我们刚刚说的没有偏序的时候比较关系对应。

然后子树内节点编号一定是递增的，因此我们找一颗树的 sz 只需要找到根的位置，然后二分一个以他为起点的前缀满足编号都 \(\ge x\) 即可。

另：括号序列可以更好地描述子树，找到根对应的左右括号即可确定子树位置。但是对于有序插入儿子，仍需要维护关于儿子的一个数据结构，或者直接像刚才一样做就行了。

DAY2

模拟赛 T1：

• 暴力维护：

  绝对深度不同限制不同，然后相同的按照 dfn 排序，树剖，每次修改的 dfn 是区间，二分出来改就行了。

• 优美线性：

  注意我们相当于要求子树 k 邻域必须有点，容易发现不会出现有交但不包含的情况，包含的满足小的即可。

  然后每个点之多处于一个区间内，然后扫描线即可。

模拟赛 T2：

不会，傻逼题。

怎么这么多人吊打国家队。

模拟赛 T3：

不会，哇哈天擦你傻呀。