tarjan--割点

不赘叙了，问就是找图里的割点。

运用tarjan算法，维护dfn[] 和 low[] 两个数组，

 

先说结论吧，就是：

一个割点，他的所有子节点的low值都会大于等于该割点的dfn值，

也即，对于边（u，v），存在有low[v]>=dfn[u]，则u为割点。

 

分析如下：

分为根节点和非根节点来讨论：

1.根节点，很显然，满足其子树>=2则该根节点为割点，因为去掉了这个根节点，其子树也就互不相连，该图就不是连通图了。

（注意子树的定义：互不连通，无返回根节点的路）

2.非根节点，就得用上面所说的结论了，

因为，对于u点是否是割点，从边(u，v)考虑，

如果所有的v能够到达u的祖先，那么low[v]就会变成dfn[u的祖先节点]，则一定会比dfn[u]小，此时去掉u仍是连通图。

也即low[v]<dfn[u]，则u不是割点。

反之，若存在low[v]>=dfn[u]也就意味着，子节点v无法到达u的祖先节点，那么u就是割点。

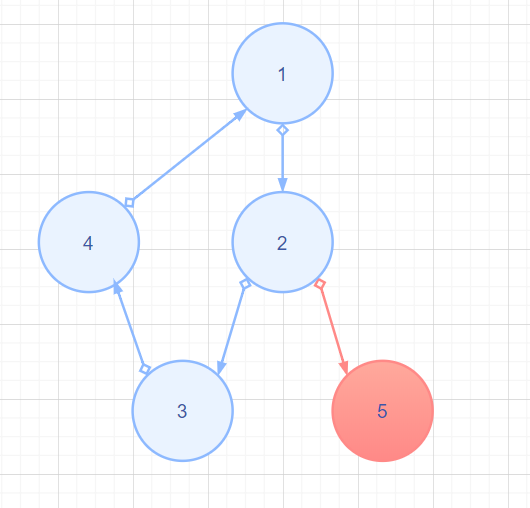
看图理解吧，对于非根节点2，

先说红边（2，5）和节点5都不存在的情况，对于节点2的子节点3，4可以到达节点2的祖先，也就是其low值都会比dfn[2]小（会变成dfn[1]）

也就是说，对于节点2，不符合存在low[子节点]>=dfn[割点]。

那么节点2就不是割点（本身也可以看出，去掉节点2，图仍然是连通图）

 

如果红边（2，5）和节点5存在，那么子节点5无法到达节点2的祖先，那么low[5]就会大于dfn[2]，

也就是说，对于节点2，符合存在low[子节点]>=dfn[割点]。

那么节点2就是割点，（本身也可以看出，去掉节点2，图就不再是连通图，节点5孤立）

 下面上代码：（用的vector存图）

void tarjan(int u,int r)//当前搜索树节点为u，根节点为r
{
    dfn[u]=low[u]=++cnt;
    int child=0;//当前子树的数量 
    for(int i=0;i<mp[u].size();++i)
    {
        int v=mp[u][i];
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]&&u!=r)vc.push_back(u);//存在 low[v]>=dfn[u] 且 不是根节点 ，则是割点 
            if(u==r)child++;
        }
        low[u]=min(low[u],dfn[v]);
    }
    if(child>=2&&u==r)vc.push_back(u);//根节点 且 子树>=2 ，则是割点 
}

例题：https://www.luogu.com.cn/problem/P3388

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<queue>
#include<cmath>
#include<map>
#include<algorithm>
using namespace std;
#define N 20210
#define mt(x) memset(x,0,sizeof x)
typedef long long ll;
void cn(ll x){cout<<x<<endl;}
void cs(string x){cout<<x<<endl;}
int n,m;
vector<int>vc,mp[N];
int dfn[N],low[N],vis[N],cnt;
//vis防止重复选择节点 
void init()
{
    cin>>n>>m;
    for(int i=1;i<=m;++i)
    {
        int x,y;
        cin>>x>>y;
        mp[x].push_back(y);
        mp[y].push_back(x);//无向图 
    }
    mt(vis);
}
void tarjan(int u,int r)
{
    dfn[u]=low[u]=++cnt;
    int child=0;//当前子树的数量 
    for(int i=0;i<mp[u].size();++i)
    {
        int v=mp[u][i];
        if(!dfn[v])
        {
            tarjan(v,r);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]&&u!=r&&!vis[u])
            {
                vis[u]=1;
                vc.push_back(u);
            }
            if(u==r)child++;
        }
        low[u]=min(low[u],dfn[v]);
//        if(low[v]>=dfn[u]&&u!=r&&!vis[u])
//        {
//            vis[u]=1;
//            vc.push_back(u);
//        }
//        if(u==r)child++; 
//      写在如上位置不具有子节点判断的意思 
    }
    if(child>=2&&u==r&&!vis[u])
    {
        vis[u]=1;
        vc.push_back(u);
    }
}
void solve()
{
    init();
    for(int i=1;i<=n;++i)
        if(!dfn[i])tarjan(i,i);
    sort(vc.begin(),vc.begin()+vc.size());
    cn(vc.size());
    for(int i=0;i<vc.size();++i)
    {
        if(i)cout<<' '; 
        cout<<vc[i];
    }
    cs("");
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    solve();
    return 0;
}