算法第二章上机实践报告

    以下的内容将围绕PTA上算法第二章实践的三道题目， 主要针对7-1题 分为实践题目、问题描述、算法描述、算法时间及空间复杂度分析和心得体会五大部分作实践报告。在此特别感谢和我一起上机的小伙伴唐伟严和王恬萌，三个人的默契与合作使得我们高效率地完成了此次实践作业。

 

7-1 二分查找

 

 

一、实践题目

 

 

二、问题描述

（1）题目关键词：n值 n个整数 非降序排列 二分查找 下标及比较次数

（2）思路：先为即将输入的数组申请一个整型变量空间，再输入想要查找的数，通过二分查找算法确定先前输入的数组中中间位置的数。将中间位置的数与查找的数作比较，如果两者相等，则查找成功；否则利用中间位置的数将数组分成前、后两个子数组，如果中间位置的数大于查找的数，则进一步查找前一子数组，否则进一步查找后一子数组。查找成功后输出数对应的下标及比较次数，查找失败则输出-1及比较次数。通过定义整型count对比较次数进行记录，经过一次二分查找后count的数量级+1。

 

三、算法描述

#include<iostream>

using namespace std;

 

int main()

{

　　int n, x, t;

　　cin>>n;

    int *a=new int[n];

　　for(int i=0;i<n;i++)

　　{

　　　　cin>>a[i];

　　}

　　cin>>x;

　　int left=0,right=n-1,mid;

　　int count=0;

　　while(right-left>=0)

　　{

　　　　mid=(left+right)/2;

　　　　if(x==a[mid])

　　　　{

　　　　　　cout<<mid<<endl;

　　　　　　left=0;

　　　　　　right=-1;

　　　　}

　　　　else if(x<a[mid])

　　　　{

　　　　　　right=mid-1;

　　　　}

　　　　else

　　　　{

　　　　　　left=mid+1;

　　　　}

　　　　count++;

　　}

　　if(right<left&&x!=a[mid]) cout<<-1<<endl;

　　cout<<count;

　　return 0;

}

四、算法时间及空间复杂度分析

 

时间复杂度：O(n) = O(log2n)

假使总共有n个元素，每执行一次算法的while循环，待搜索数组的大小减小一半，即二分后每次查找的区间大小为n，n/2，n/4，…，n/2^k（接下来操作元素的剩余个数），其中k是循环的次数。 

最坏的情况是看k次二分之后,每个区间的大小为1,则令n/2^k=1，可得k=log2n，所以时间复杂度表示为O(n)=O(log2n)。

 

空间复杂度：0(n) = 1

 

二分查找整个运算过程空间大小没有发生改变。

 

 

五、心得体会

这道二分查找的题目核心在于如何界定二分查找的条件以及如何实现二分查找算法。二分查找的核心算法相对比较容易掌握，但是在书写代码的过程中我还是遇到了以下几个问题：

第一，在二分查找循环的过程中，在中间位置的数与查找的数进行一轮比较后，一开始忘记对left和right值重新初始化导致输出的结果有误；

第二，对每次循环后count计数的代码书写位置仍不明确，即对循环的概念存在模糊的地方，对代码实现的整个思路不够清晰；

第三，忽视了查找的数在数组中不存在时多条件即right<left&&x!=a[mid]成立才能输出的情况，导致无论查找成功还是失败对应的内容仍然会输出。

在下次遇到类似的题目及问题时应对以上内容更加重视，在对所有需要满足的条件考虑周全理清思绪以后再完整书写源程序代码。

 

 

（以下部分有时间会继续补充）

7-2 改写二分搜索算法 

 

一、实践目的（与7-1相似）

 

（1）掌握二分搜索的工作原理及应用过程； 

（2）提高程序运行和查找的效率，减少数据的比较次数； 

（3）掌握二分搜索算法的基本步骤，学会用该算法解决实际问题。

 

二、题目内容

 

 

 

三、问题分析 

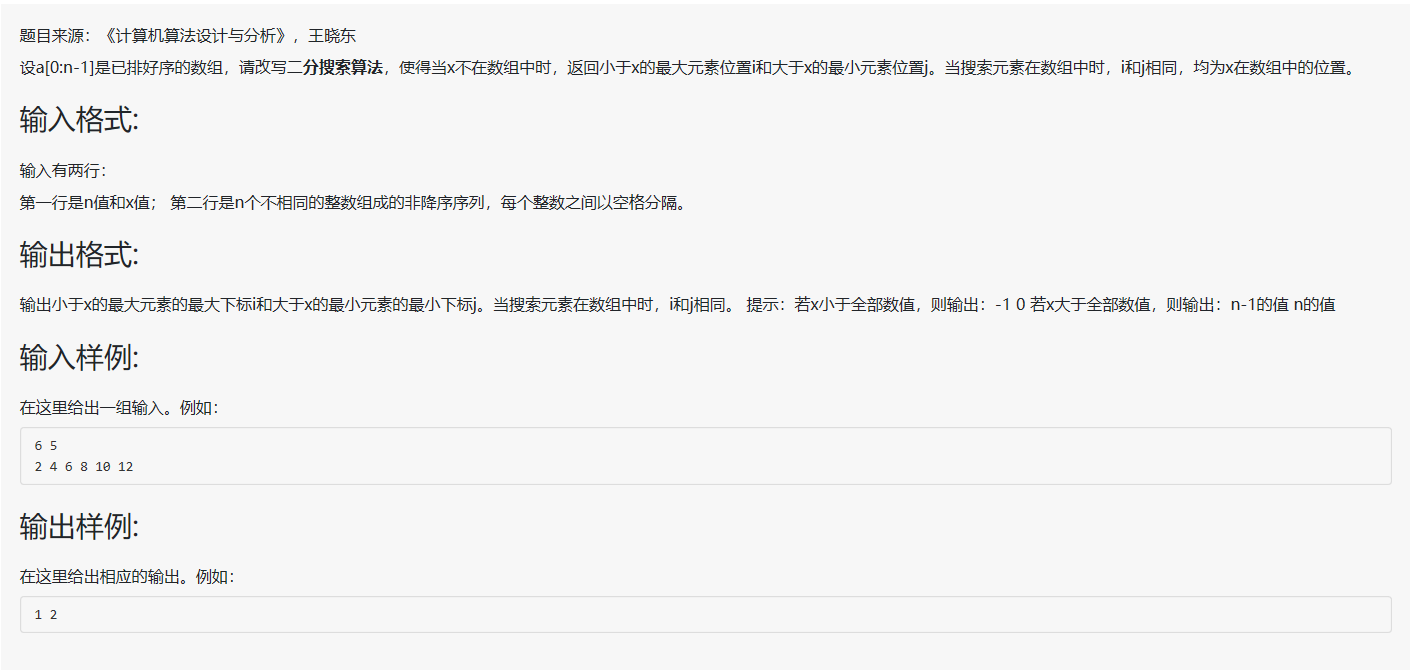
（1）题目关键词：数组 排好序 二分搜索算法 小于x的最大元素位置 大于x的最小元素位置 x在数组中的位置

 

（2）思路：（与7-1相似）先为即将输入的数组申请一个整型变量空间，再输入想要查找的数x，通过二分查找算法确定先前输入的数组中中间位置的数。将中间位置的数与查找的数作比较，如果两者相等，则查找成功；否则利用中间位置的数将数组分成前、后两个子数组，如果中间位置的数大于查找的数，则进一步查找前一子数组，否则进一步查找后一子数组。查找成功后重复输出两次数对应的下标，查找失败后分三种情况输出：若x小于全部数值，则输出：-1 0；若x大于全部数值，则输出：数组中第二大的数和第一大的数对应的下标，即n-1的值 n的值；否则输出：小于x的最大元素位置i和大于x的最小元素位置j。

 

 

四、源程序代码

 

#include<iostream> 

using namespace std;

 

int main()

{

　　int n, x;

　　cin>>n>>x;

　　int *a=new int[n];

　　for(int i=0;i<n;i++)

　　{

　　　　cin>>a[i];

　　}

　　if(x<a[0]) cout<<-1<<" "<<0;

　　if(x>a[n-1]) cout<<n-1<<" "<<n;

　　int left=0,right=n-1,mid;

　　while(right-left>=0&&x>=a[0]&&x<=a[n-1])

　　{

　　　　mid=(left+right)/2;

    　　if(x==a[mid])

    　　{

　　　　　　cout<<mid<<" "<<mid<<endl;

　　　　　　left=0;

　　　　　　right=-1;

　　　　}

　　　　else if(x<a[mid])

    　　{

　　　　　　right=mid-1;

　　　　}

　　　　else

　　　　{

　　　　　　left=mid+1;

　　　　}

　　}

　　if(right<left&&x!=a[mid]&&x>=a[0]&&x<=a[n-1]) cout<<right<<" "<<left;

　　return 0;   

}

 

五、经验总结 

比较明显的问题及改进： 

（1）代码层次感不够强，不够精简，对可能存在的条件预判不够准确，导致书写if语句条件时会有重复的内容出现，以后多练习类似题目，写前想清楚代码实现的整个过程，锻炼相应的思维能力；

 

（2）为了保证输出结果与给的样例相符才互换了left和right进行输出，实际上对于为什么要互换才能保证正确输出理解还不够透彻，后来才知道是因为整个数组被搜索完毕之后left的值继续增加，right的值继续减少，该操作导致left的值比right的大，也相当于left和right的值发生了交换，所以要逆序输出才匹配。

 

7-3 两个有序序列的中位数

 

一、实践目的

（1）掌握二分搜索的工作原理及应用过程；

（2）提高程序运行和查找的效率，减少数据的比较次数，控制算法的时间复杂度为O(n)；

（3）掌握二分搜索算法的基本步骤，学会在短时间内用该算法解决查找两组数组合并后的中位数的问题。

 

二、题目内容

 

 

三、问题分析

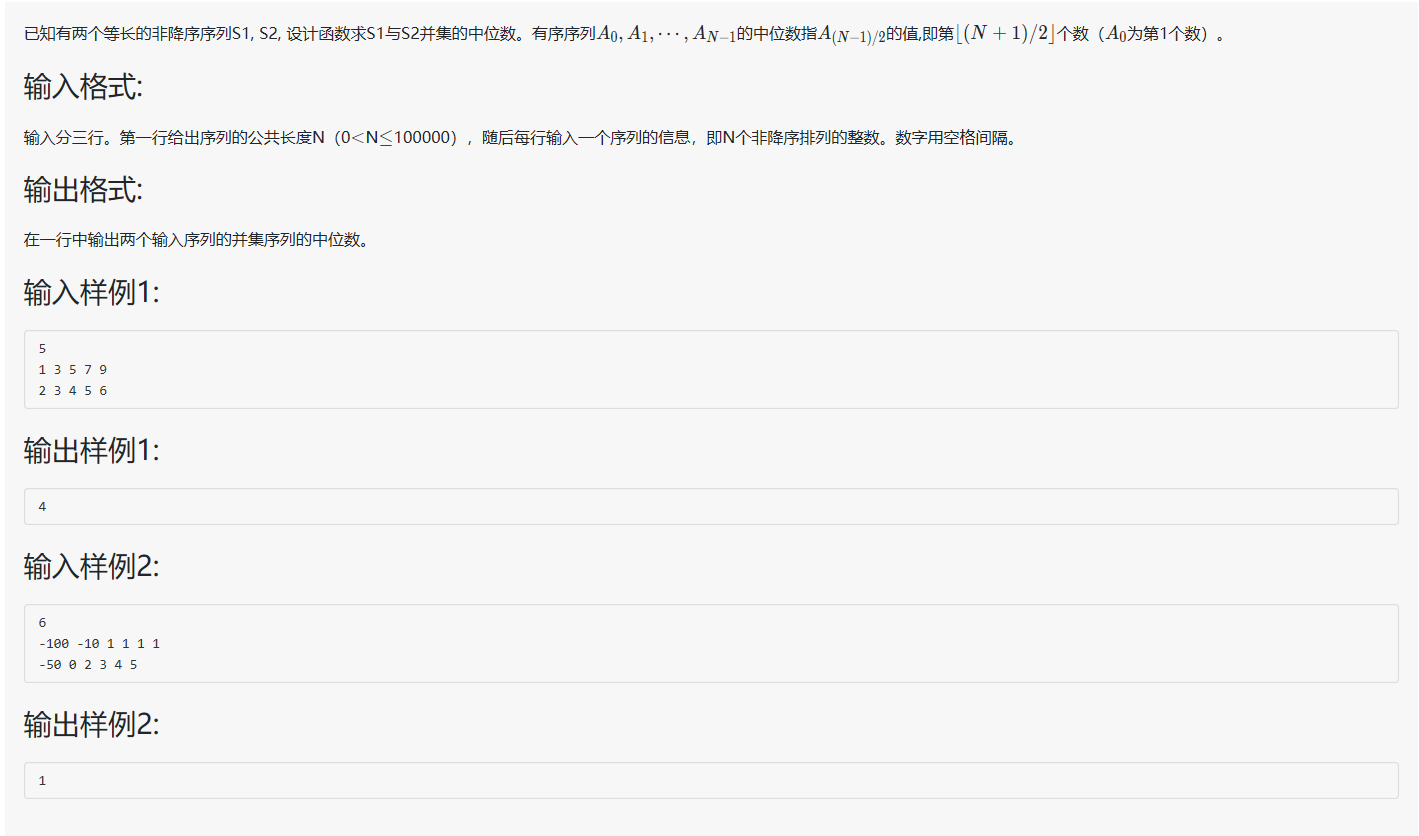
（1）题目关键词：两个非降序序列 等长 并集 中位数

（2）思路：（未完待续）

 

四、源程序代码

法一：

#include<iostream>

using namespace std;

 

void merge(int* a, int l, int m, int r)

{

    int b[200000];

    int i=l, j=m+1, k=l;

    while((i<=m)&&(j<=r))

    {

        if(a[i]<=a[j])

        {

            b[k++]=a[i++];

        }

        else 

        {

            b[k++]=a[j++];

        }

    }

    if(i>m)

    {

        for(int p=j;p<=r;p++)

        {

            b[k++]=a[p];

        }

    }   

    else

    {

        for(int p=i;p<=m;p++)

        {

            b[k++]=a[p];

        }

    }

    for(int p=l;p<=r;p++)

    {

        a[p]=b[p];

    }

}

 

void mergeSort(int* a, int l, int r)

{

    if(l>=r) return;

    else 

    {

        int m=(l+r)/2;

        mergeSort(a, l, m);

        mergeSort(a, m+1, r);

        merge(a, l, m, r);

    }

}

 

int main()

{

    int n;

    cin>>n;

　　int *a=new int[n];

　　int *b=new int[n];

　　int *c=new int[2*n];

    for(int i=0;i<n;i++)

    {

        cin>>a[i];

        c[i]=a[i];

    }

    for(int i=0;i<n;i++)

    {

        cin>>b[i];

        c[n+i]=b[i];

    }

    mergeSort(c, 0, 2*n-1);

    int d=(2*n+1)/2;

    cout<<c[d-1];

    return 0;

}

（未完待续）