Two Buildings[决策单调性+分治]

参考链接：https://blog.csdn.net/weixin_45819197/article/details/115015851

这篇文章已经写得很清楚了。我整理下用自己的语言（部分直接粘贴）写一遍，加深下印象。

 

题意：数组h长度n（n<=1e6）。h[i]<=1e6。求max(（h[i]+h[j]）*(j-i));

 

决策单调性：

对于任意的a<b<c<d，如果满足在c处转移到b比a优，那么在d处也满足。

一个决策如果比另一个决策劣，那么这个决策一定不再是最优决策。决策单调性优化是为每个决策点分配对应的决策区间。

 

步骤一：转化题意为求最大矩形面积

题目求的是（h[i]+h[j]）*(j-i)的值

抛开这个，我们看一个式子 (b[j]-a[i])*(j-i)。假定，a数组和b数组各自记录了n个坐标。数组下标为横坐标，数组值为纵坐标。那么该式子代表的就是a[i]和b[j]为对角线的矩形的面积（当b[j]>a[i]且j>i时）。

并且我们发现，这个式子和题目所求式子有相似之处。将b[j]转化为h[j]， a[i]转化为-h[i]，就可以将题目转化为求 矩形面积了。

只需要On的时间复杂度去得到a、b数组。

 

步骤二：求最大矩形面积

得到a、b数组的点之后我们来求最大矩形面积。

步骤2-1：决策单调性筛数据

 

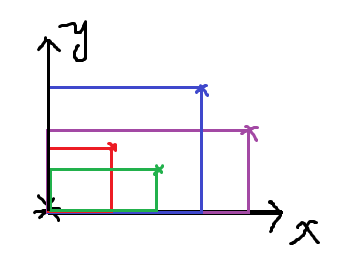
 来看一个例子。图中有 黑、红、绿、蓝、紫五个点。现在以黑点为左下角的点，在其他点中找和黑点所连对角线的矩形最大的点。我们可以发现，蓝点肯定优于红点，因为蓝黑构成的矩形覆盖了红黑矩形。同理，紫点优于红点。即当固定一个左下角点去寻找右上角点的时候，横坐标和纵坐标都大的数据更优。

因此，我们在筛选右上角点的时候，可以从横坐标最小的点开始筛选，判断下其后有没有纵坐标更大的点，如果有代表有更优的点，那么当前点不必保留。

同理，我们在筛左下角点的时候，可以从横坐标最大的点开始筛选，判断其前有没有纵坐标更小的点，如果有就不必保留当前点。

以a数组为例，怎么筛选呢。朴素做法是On²，对每个点i都判断其前面（即左边）有没有点纵坐标比当前小，如果有就舍弃，反之保留。但是这样会超时。

对于a数组，我们可以用一个minv来记录当前记录到的最低纵坐标，然后从左往右扫。一旦遇到比纵坐标minv大的点，必然舍弃。【这个也挺巧的 我太傻了 只会暴力On²】

b数组类似。

最后，我们在On复杂度内得到了筛完无用数据的a数组和b数组。

 

步骤2-2：分治找最优（如何证明）

规则：在a数组中找一点s（a数组中代表的是左下角点），在b数组中找一点t（b数组中代表的是右上角点），使t是b数组中的点和a相连的对角线对应矩形面积最大的点。那么，对于在a数组中s点左边的点s‘，b数组中对其最优的t’一定在t左边；同理，对于s点右边的点s‘，b中最优点t’也一定在t右边。

方法：根据这个规则，可以分治找最优。首先在a数组中取中间点mid，然后暴力遍历b数组找到最优点pos。那么最后的答案一定是，mid和pos， 1~mid和1~pos， mid~a最后一个点和pos+1~b最后一个点 三种情况中取最优。而对于1~mid和1~pos-1，  mid+1~a最后一个点和pos+1~b，我们可以继续用这个思路去分治找当前最优。

证明：

前提1：对于a数组中的点s，b数组中的t是能让以a为左下角点的矩形面积最大的点。

前提2：用S(i, j)表示以a中i点为左下角点，b中j点为右上角点构成的矩形面积。

前提3：根据步骤一中的筛选数据，我们可以发现a、b数组中的点排列趋势都是西北-东南趋势。

要证规则成立，即证对于s左边的点s‘，t右边的点t’和s‘所构成的面积都比S(s',t)小

 

 

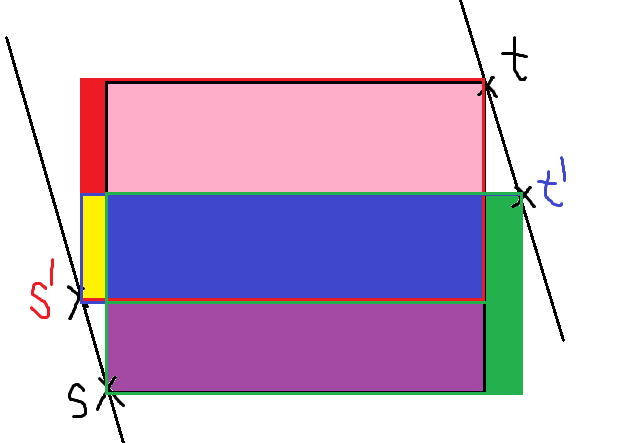
以此图为例。由于S(s,t)是和s为左下角的点的矩形的最大面积，因此可以根据S(s,t)>S()不重合面积判断粉色面积必然大于绿色面积。【粉>绿】

而

S(s',t)  =粉       +蓝+黄+红

S(s',t') =部分绿+蓝+黄

显然S(s',t)>S(s',t')

得证。

 

代码：

 

#include <stdio.h>
#include <algorithm>
#define ALL(x) x.begin(),x.end()
//#define LOCAL
using namespace std;
typedef long long ll;
const int mx=1e6+10;
const ll inf=1e15+10;
ll n;
ll h[mx], a[mx], b[mx];
struct node{
    ll x, y;
    node(){}
    node(ll x, ll y):x(x), y(y){}
    bool operator <(const node o)const{
        return x<o.x;
    }
}na[mx], nb[mx];
ll cnt1, cnt2;//筛选完后na的个数和nb的个数
ll ans;
inline ll max(ll v1, ll v2){return v1>v2?v1:v2;}
inline ll min(ll v1, ll v2){return v1<v2?v1:v2;}
ll getS(ll i, ll j){
    return (nb[j].y-na[i].y)*(nb[j].x-na[i].x);
}
void init(){
    cnt1=cnt2=ans=0;
    ll small=inf, big=-inf;
    for(int i=1;i<=n;i++){//处理a数组
        if(a[i]>=small)continue;
        na[++cnt1]=node(i,a[i]);
        small=a[i];
    }
    for(int i=n;i>=1;i--){
        if(b[i]<=big)continue;
        nb[++cnt2]=node(i, b[i]);
        big=b[i];
    }
    sort(nb+1, nb+1+cnt2);//一定要记得排序 让横坐标小的点的在nb中的下标小
}
ll solve2(ll la, ll ra, ll lb, ll rb){
    if(ra<la || rb<lb)return 0;
    ll s=(la+ra)>>1;
    ll mj=getS(s, lb), t=lb;
    for(ll i=lb+1;i<=rb;i++){
        if(nb[i].x<=na[s].x)continue;//题目要求
        ll cur=getS(s, i);
        if(cur>mj){
            mj=cur;
            t=i;
        }
    }
    ll ans1=mj;
    ll ans2=solve2(la, s-1, lb, t);
    ll ans3=solve2(s+1, ra, t, rb);
    ans1=max(ans1, ans2);
    ans1=max(ans1, ans3);
    return ans1;
}
void solve(){
    scanf("%I64d", &n);
    for(ll i=1;i<=n;i++){
        scanf("%I64d", &h[i]);
        a[i]=-h[i];b[i]=h[i];//得到点
    }
    init();//得到的筛选后的a数组和b数组
    ans=solve2(1, cnt1, 1, cnt2);
    printf("%I64d\n", ans);
}
int main(){
#ifdef LOCAL
    FILE *fp=freopen("1", "r", stdin);
#endif
    solve();
#ifdef LOCAL
    fclose(fp);
#endif
    return 0;
}