相机标定

3D视觉

3D点

X4不等于0时：

X4=0表示无穷远点

点的射影变换：

3D平面

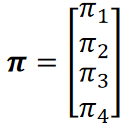
无穷远平面：

点X在平面π上：

平面的射影变换：
 

点->平面

3点确定一个平面

平面->点

3个平面确定一个交点

3D直线

连接两点A，B的直线的矩阵表示

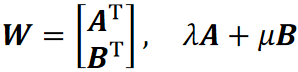
对偶表示

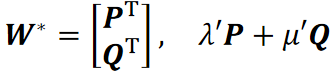
关联

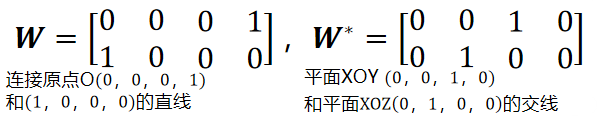
点，线，面关系

一个点X + 一条直线W确定一个平面π

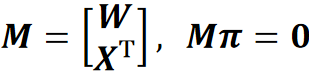
直线W与平面π的交点为X

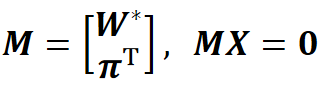
二次曲面

9个点确定一个二次曲面。

切平面：

如果Q是奇异矩阵，也就是行列式为0，那么二次曲面是退化的。

射影变换

H的确定

对绝对二次曲面进行SVD分解，H就是U

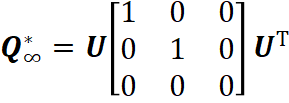
H=U

绝对二次曲线

Ω_∞是无穷远平面π_∞上的一条二次曲线。自由度为5

满足条件：

Ω_∞的方程

绝对二次曲线是π_∞上的纯虚圆。

射影变换

自由度为15

直线经过射影变换仍然是直线

射影空间性质的度量（直线和无穷远平面度量）

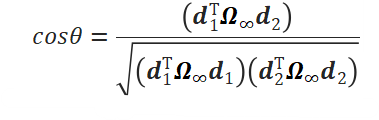
射影空间性质的度量（无穷远平面和绝对对偶二次曲面度量）

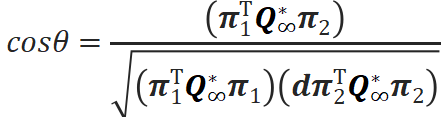
仿射变换

自由度为12

保持平面的平行性，体积比、形心不变。

一旦确定无穷远平面π_∞，就能测量三维空间仿射性质。

相似变换

自由度为7，分别为一个缩放因子s，3个旋转角度确定的旋转矩阵R，3个坐标轴的平移量t。

保持角度不变、绝对二次曲线不变

欧式变换

自由度为6

 

 

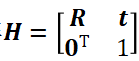
透相机 VS 针孔相机

相关术语

  

焦距越小，图像越小。  

  

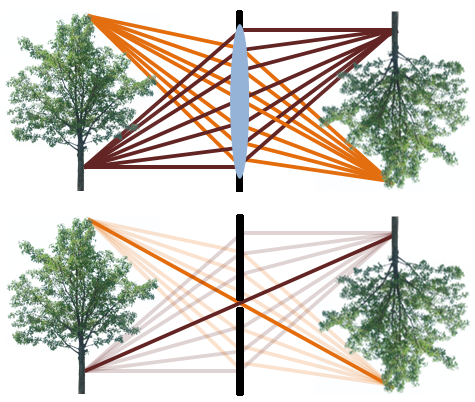
针孔越大，越模糊。

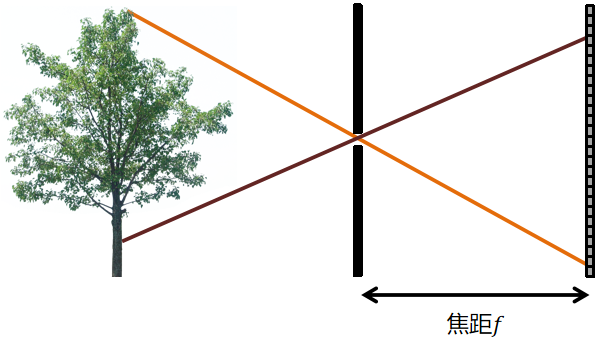
焦距

透镜相机中，焦距为平行光线相交的距离。

针孔相机中，焦距为针孔到传感器的距离。

  

 

 

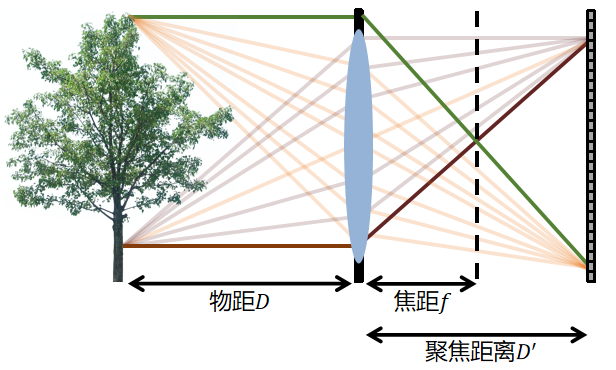
成像过程

总的过程

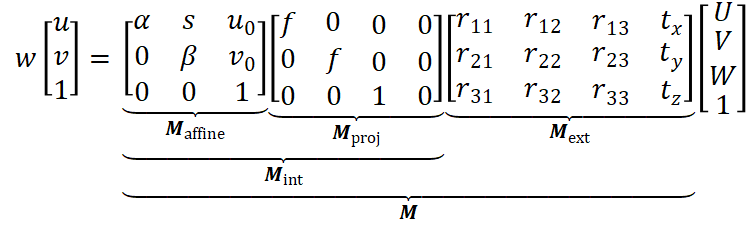
世界坐标UVW  ->  相机坐标XYZ  ->  像平面坐标xy  ->   像素坐标

世界坐标->相机坐标

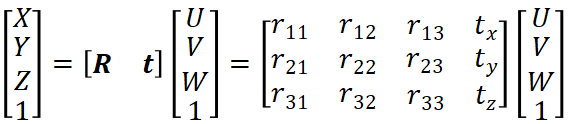
可以描述为：

R_W控制旋转，t_W控制平移。

平移

世界坐标点X_W为世界坐标原点：

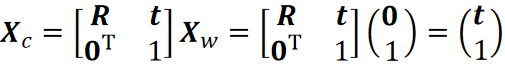
旋转

假设相机坐标系和世界坐标系的原点对齐：t=0

U轴上单位距离的点旋转：

  

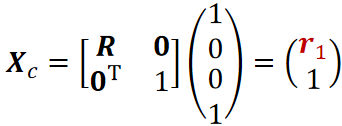
V轴上单位距离的点旋转：

  

W轴上单位距离的点旋转：

  

相机坐标 -> 图像坐标

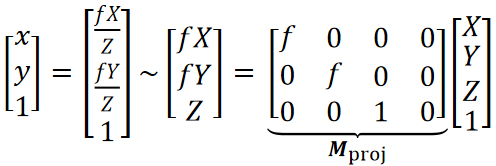
图像坐标 -> 像素坐标

假设光心位置(u₀,v₀)

平移变换：

平移+缩放

纵轴分辨率为：k像素/cm。横轴分别率为：l像素/cm

仿射变换

纵轴分辨率为：k像素/cm。横轴分别率为：l像素/cm

偏斜角为Θ

总的成像过程

相机标定

估计投影矩阵

给定N个世界坐标X₁,...,X_N以及他们对应像素的坐标x₁,...,x_N

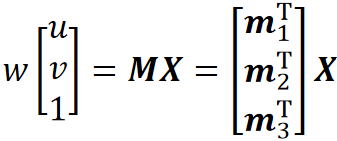
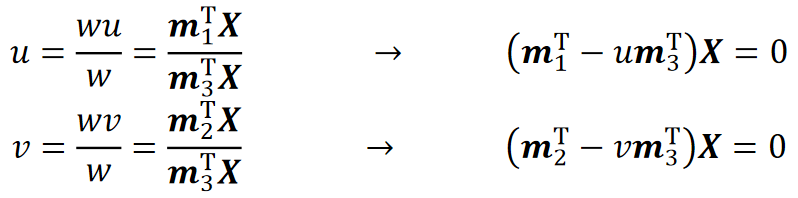
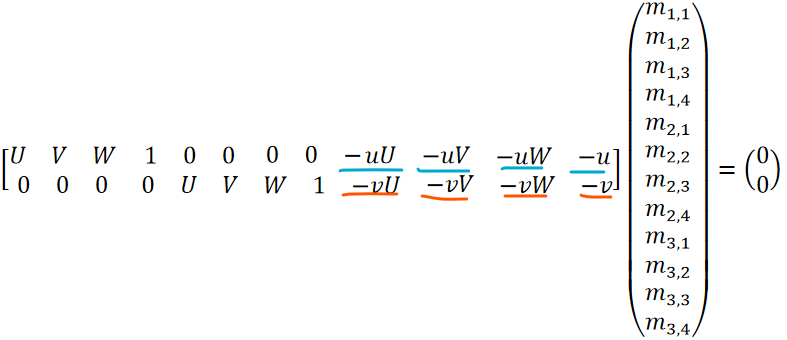
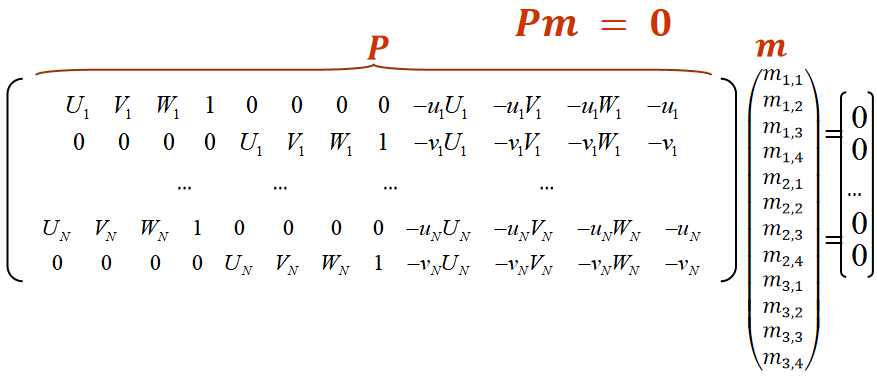
对P进行SVD分解，V的最后一列，也就是最小的特征值对应的特征向量为m

归一化DLT

对图像坐标进行归一化，平移到均值，缩放为√2

对空间坐标进行归一化，平移到均值，缩放为√3

然后采用归一化后的坐标计算DLT。