Ng第十二课:支持向量机(Support Vector Machines)(一)
1 目录
支持向量机基本上是最好的有监督学习算法了,从logistic回归出发,引出了SVM,揭示模型间的联系,过渡自然。
2 重新审视logistic回归
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特征的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
假设函数 其中x是n维特征向量,函数g就是logistic函数。
其中x是n维特征向量,函数g就是logistic函数。 的图像是
的图像是

可以看到,将无穷映射到了(0,1)。
假设函数就是特征属于y=1的概率。

当要判别一个新来的特征属于哪个类时,只需求![]() ,若大于0.5就是y=1的类,反之属于y=0类。
,若大于0.5就是y=1的类,反之属于y=0类。
再审视一下![]() ,发现
,发现![]() 只和
只和![]() 有关,
有关,![]() >0,那么
>0,那么![]() ,g(z)只不过是用来映射,真实的类别决定权还在
,g(z)只不过是用来映射,真实的类别决定权还在![]() 。还有当
。还有当![]() 时,
时,![]() =1,反之
=1,反之![]() =0。如果只从
=0。如果只从![]() 出发,希望模型达到的目标无非就是让训练数据中y=1的特征
出发,希望模型达到的目标无非就是让训练数据中y=1的特征![]() ,y=0的特征
,y=0的特征![]() 。Logistic回归就是要学习得到
。Logistic回归就是要学习得到![]() ,使得正例的特征远大于0,负例的特征远小于0,强调在全部训练实例上达到这个目标。
,使得正例的特征远大于0,负例的特征远小于0,强调在全部训练实例上达到这个目标。
图形化表示如下:

中间那条线是![]() ,logistic回顾强调所有点尽可能地远离中间那条线。学习出的结果也就中间那条线。考虑上面3个点A、B和C。从图中可以确定A是×类别的,然而C我们是不太确定的,B还算能够确定。这样可以得出结论,我们更应该关心靠近中间分割线的点,让他们尽可能地远离中间线,而不是在所有点上达到最优。这大概就是支持向量机的思路和logistic回归的不同点。
,logistic回顾强调所有点尽可能地远离中间那条线。学习出的结果也就中间那条线。考虑上面3个点A、B和C。从图中可以确定A是×类别的,然而C我们是不太确定的,B还算能够确定。这样可以得出结论,我们更应该关心靠近中间分割线的点,让他们尽可能地远离中间线,而不是在所有点上达到最优。这大概就是支持向量机的思路和logistic回归的不同点。
3 形式化表示
这次使用的结果标签是y=-1,y=1替换在logistic回归中使用的y=0和y=1。同时将![]() 替换成w和b(
替换成w和b(![]() 0)。以前的
0)。以前的![]() ,其中认为
,其中认为![]() ,替换
,替换![]() 为b,后面替换
为b,后面替换![]() 为
为![]() (即
(即![]() )。这样,我们让
)。这样,我们让![]() ,进一步
,进一步![]() = hw,b(x)。
= hw,b(x)。
上一节提到过只需考虑![]() 的正负问题,而不用关心g(z),因此这里将g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系如下:
的正负问题,而不用关心g(z),因此这里将g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系如下:
4 函数间隔和几何间隔
给定一个训练样本![]() ,x是特征,y是结果标签。i表示第i个样本。定义函数间隔如下:
,x是特征,y是结果标签。i表示第i个样本。定义函数间隔如下:
当![]() 时,又
时,又![]() (直线图的例子全在第一象限),
(直线图的例子全在第一象限),![]() 的值实际上就是
的值实际上就是![]() (该情况下永为正值)。反之亦然(-1)。为了使函数间隔最大(更大的信心确定该例是正例还是反例),当
(该情况下永为正值)。反之亦然(-1)。为了使函数间隔最大(更大的信心确定该例是正例还是反例),当![]() 时,
时,![]() 应该是个大正数,反之是个大负数。因此函数间隔代表了我们认为特征是正例还是反例的确信度。
应该是个大正数,反之是个大负数。因此函数间隔代表了我们认为特征是正例还是反例的确信度。
继续考虑w和b,如果同时加大w和b,比如在![]() 前面乘个系数比如2,那么所有点的函数间隔都会增大二倍,这个对求解问题来说不应该有影响,因为我们要求解的是
前面乘个系数比如2,那么所有点的函数间隔都会增大二倍,这个对求解问题来说不应该有影响,因为我们要求解的是![]() (那根直线),同时扩大w和b对结果是无影响的。这样,但也要限制w和b,可能需要加入归一化条件,毕竟求解的目标是确定唯一一个w和b,而不是多组线性相关的向量。这个归一化一会再考虑。
(那根直线),同时扩大w和b对结果是无影响的。这样,但也要限制w和b,可能需要加入归一化条件,毕竟求解的目标是确定唯一一个w和b,而不是多组线性相关的向量。这个归一化一会再考虑。
刚刚我们定义的函数间隔是针对某一个样本的,现在我们定义全局样本上的函数间隔
![]() ,说白了就是在训练样本上分类正例和负例确信度最小那个函数间隔。
,说白了就是在训练样本上分类正例和负例确信度最小那个函数间隔。
接下来定义几何间隔,先看图

假设我们有了B点所在的![]() 分割面。任何其他一点,比如A到该面的距离以
分割面。任何其他一点,比如A到该面的距离以![]() 表示,假设B就是A在分割面上的投影。我们知道向量BA的方向是
表示,假设B就是A在分割面上的投影。我们知道向量BA的方向是![]() (分割面的梯度),单位向量是
(分割面的梯度),单位向量是![]() 。A点是
。A点是![]() ,所以B点是x=
,所以B点是x=![]() (利用初中的几何知识),带入
(利用初中的几何知识),带入![]() 得,
得,
进一步得到
再换种更加优雅的写法:
当![]() 时,不就是函数间隔吗?是的,前面提到的函数间隔归一化结果就是几何间隔。他们为什么会一样呢?因为函数间隔是我们定义的,在定义的时候就有几何间隔的色彩。同样,同时扩大w和b,w扩大几倍,
时,不就是函数间隔吗?是的,前面提到的函数间隔归一化结果就是几何间隔。他们为什么会一样呢?因为函数间隔是我们定义的,在定义的时候就有几何间隔的色彩。同样,同时扩大w和b,w扩大几倍,![]() 就扩大几倍,结果无影响。同样定义全局的几何间隔
就扩大几倍,结果无影响。同样定义全局的几何间隔![]()
5 最优间隔分类器(optimal margin classifier)
前面提到的目标是寻找一个超平面,使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面,我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。形式化表示为:
到此,已经将模型定义出来了。如果求得了w和b,那么来一个特征x,就能够分类了,称为最优间隔分类器。
接下的问题就是如何求解w和b的问题了。由于![]() 不是凸函数,我们想先处理转化一下,考虑几何间隔和函数间隔的关系,
不是凸函数,我们想先处理转化一下,考虑几何间隔和函数间隔的关系,![]() ,我们改写一下上面的式子:
,我们改写一下上面的式子:
这个时候目标函数仍然不是凸函数,没法直接代入优化软件里计算。我们还要改写。前面说到同时扩大w和b对结果没有影响,但我们最后要求的仍然是w和b的确定值,因此就需要对![]() 做一些限制,以保证解是唯一的。这里为了简便取
做一些限制,以保证解是唯一的。这里为了简便取![]() ,这样的意义是将全局的函数间隔定义为1,也即是将离超平面最近的点的距离定义为
,这样的意义是将全局的函数间隔定义为1,也即是将离超平面最近的点的距离定义为![]() 。由于求
。由于求![]() 的最大值相当于求
的最大值相当于求![]() 的最小值,因此改写后结果为:
的最小值,因此改写后结果为:
这下好了,只有线性约束了,而且是个典型的二次规划问题(目标函数是自变量的二次函数)。代入优化软件可解。
(虽然没有图解那么直观,但每一步推导有理有据,依靠思路的流畅性来推导出目标函数和约束。)
接下来介绍的是手工求解的方法了,一种更优的求解方法。
6 拉格朗日对偶(Lagrange duality)
先抛开上面的二次规划问题,先来看看存在等式约束的极值问题求法,比如下面的最优化问题:
![clip_image001[9] clip_image001[9]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131234477453.png)
目标函数是f(w),下面是等式约束。通常解法是引入拉格朗日算子,这里使用![]() 来表示算子,得到拉格朗日公式为
来表示算子,得到拉格朗日公式为
![clip_image004[6] clip_image004[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131234483700.png)
L是等式约束的个数。
至于为什么引入拉格朗日算子可以求出极值,原因是f(w)的dw变化方向受其他不等式的约束,dw的变化方向与f(w)的梯度垂直时才能获得极值,而且在极值处,f(w)的梯度与其他等式梯度的线性组合平行,因此他们之间存在线性关系。
然后探讨有不等式约束的极值问题求法,问题如下:
![clip_image007[6] clip_image007[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131234511451.png)
定义一般化的拉格朗日公式
这里的![]() 和
和![]() 都是拉格朗日算子。如果按这个公式求解,会出现问题,因为要求解的是最小值,而这里的
都是拉格朗日算子。如果按这个公式求解,会出现问题,因为要求解的是最小值,而这里的![]() 已经不是0了,可以将
已经不是0了,可以将![]() 调整成很大的正值,来使最后的函数结果是负无穷。因此需要排除这种情况,定义下面的函数:
调整成很大的正值,来使最后的函数结果是负无穷。因此需要排除这种情况,定义下面的函数:
![]()
这里的P代表primal。假设![]() 或者
或者![]() ,那么总是可以调整
,那么总是可以调整![]() 和
和![]() 来使得
来使得![]() 有最大值为正无穷。而只有g和h满足约束时,
有最大值为正无穷。而只有g和h满足约束时,![]() 为f(w)。这个函数的精妙之处在于
为f(w)。这个函数的精妙之处在于![]() ,而且求极大值。
,而且求极大值。
因此可以写作
![]()
![]()
使用![]() 来表示
来表示![]() 。如果直接求解,首先面对的是两个参数,而
。如果直接求解,首先面对的是两个参数,而![]() 也是不等式约束,然后再在w上求最小值。这个过程不容易做,那么怎么办呢?
也是不等式约束,然后再在w上求最小值。这个过程不容易做,那么怎么办呢?
D的意思是对偶,![]() 将问题转化为先求拉格朗日关于w的最小值,将
将问题转化为先求拉格朗日关于w的最小值,将![]() 和
和![]() 看作是固定值。之后在
看作是固定值。之后在![]() 求最大值的话:
求最大值的话:
这个问题是原问题的对偶问题,相对于原问题只是更换了min和max的顺序,而一般更换顺序的结果是Max Min(X) <= MinMax(X)。然而在这里两者相等。用![]() 来表示对偶问题如下:
来表示对偶问题如下:
![]()
下面解释在什么条件下两者会等价。假设f和g都是凸函数,h是仿射的(affine,![]() )。并且存在w使得对于所有的i,
)。并且存在w使得对于所有的i,![]() 。在这种假设下,一定存在
。在这种假设下,一定存在![]() 使得
使得![]() 是原问题的解,
是原问题的解,![]() 是对偶问题的解。还有
是对偶问题的解。还有![]() 另外,
另外,![]() 满足库恩-塔克条件(Karush-Kuhn-Tucker, KKT condition),该条件如下:
满足库恩-塔克条件(Karush-Kuhn-Tucker, KKT condition),该条件如下:
![clip_image048[6] clip_image048[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235189201.png)
所以如果![]() 满足了库恩-塔克条件,那么他们就是原问题和对偶问题的解。让我们再次审视公式(5),这个条件称作是KKT dual complementarity条件。这个条件隐含了如果
满足了库恩-塔克条件,那么他们就是原问题和对偶问题的解。让我们再次审视公式(5),这个条件称作是KKT dual complementarity条件。这个条件隐含了如果![]() ,那么
,那么![]() 。也就是说,
。也就是说,![]() 时,w处于可行域的边界上,这时才是起作用的约束。而其他位于可行域内部(
时,w处于可行域的边界上,这时才是起作用的约束。而其他位于可行域内部(![]() 的)点都是不起作用的约束,其
的)点都是不起作用的约束,其![]() 。这个KKT双重补足条件会用来解释支持向量和SMO的收敛测试。
。这个KKT双重补足条件会用来解释支持向量和SMO的收敛测试。
这部分内容思路比较凌乱,还需要先研究下《非线性规划》中的约束极值问题,再回头看看。KKT的总体思想是将极值会在可行域边界上取得,也就是不等式为0或等式约束里取得,而最优下降方向一般是这些等式的线性组合,其中每个元素要么是不等式为0的约束,要么是等式约束。对于在可行域边界内的点,对最优解不起作用,因此前面的系数为0。
7 最优间隔分类器(optimal margin classifier)
重新回到SVM的优化问题:
![clip_image057[6] clip_image057[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235229818.png)
我们将约束条件改写为:
![]()
从KKT条件得知只有函数间隔是1(离超平面最近的点)的线性约束式前面的系数![]() ,也就是说这些约束式
,也就是说这些约束式![]() ,对于其他的不在线上的点(
,对于其他的不在线上的点(![]() ),极值不会在他们所在的范围内取得,因此前面的系数
),极值不会在他们所在的范围内取得,因此前面的系数![]() .注意每一个约束式实际就是一个训练样本。
.注意每一个约束式实际就是一个训练样本。
看下面的图:
![clip_image067[6] clip_image067[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235267786.png)
实线是最大间隔超平面,假设×号的是正例,圆圈的是负例。在虚线上的点就是函数间隔是1的点,那么他们前面的系数![]() ,其他点都是
,其他点都是![]() 。这三个点称作支持向量。构造拉格朗日函数如下:
。这三个点称作支持向量。构造拉格朗日函数如下:
![clip_image068[6] clip_image068[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235281633.png)
注意到这里只有![]() 没有
没有![]() 是因为原问题中没有等式约束,只有不等式约束。
是因为原问题中没有等式约束,只有不等式约束。
下面按照对偶问题的求解步骤来一步步进行,
![]()
首先求解![]() 的最小值,对于固定的
的最小值,对于固定的![]() ,
,![]() 的最小值只与w和b有关。对w和b分别求偏导数。
的最小值只与w和b有关。对w和b分别求偏导数。
![clip_image071[6] clip_image071[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235339186.png)
![clip_image072[6] clip_image072[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235346088.png)
并得到
![clip_image073[6] clip_image073[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235346579.png)
将上式带回到拉格朗日函数中得到,此时得到的是该函数的最小值(目标函数是凸函数)
代入后,化简过程如下:


最后得到
![clip_image074[6] clip_image074[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235354876.png)
由于最后一项是0,因此简化为
![clip_image075[6] clip_image075[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235352302.png)
此时的拉格朗日函数只包含了变量![]() 。然而我们求出了
。然而我们求出了![]() 才能得到w和b。
才能得到w和b。
前面提到过对偶问题和原问题满足的几个条件,首先由于目标函数和线性约束都是凸函数,而且这里不存在等式约束h。存在w使得对于所有的i,![]() 。因此,一定存在
。因此,一定存在![]() 使得
使得![]() 是原问题的解,
是原问题的解,![]() 是对偶问题的解。在这里,求
是对偶问题的解。在这里,求![]() 就是求
就是求![]() 了。
了。
![]()
即可求出b。即离超平面最近的正的函数间隔要等于离超平面最近的负的函数间隔。
关于上面的对偶问题如何求解,将留给下一篇中的SMO算法来阐明。
这里考虑另外一个问题,由于前面求解中得到
![clip_image086[6] clip_image086[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/20110313123548981.png)
我们通篇考虑问题的出发点是![]() ,根据求解得到的
,根据求解得到的![]() ,我们代入前式得到
,我们代入前式得到
![clip_image089[6] clip_image089[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235502419.png)
也就是说,以前新来的要分类的样本首先根据w和b做一次线性运算,然后看求的结果是大于0还是小于0,来判断正例还是负例。现在有了![]() ,我们不需要求出w,只需将新来的样本和训练数据中的所有样本做内积和即可。那有人会说,与前面所有的样本都做运算是不是太耗时了?其实不然,我们从KKT条件中得到,只有支持向量的
,我们不需要求出w,只需将新来的样本和训练数据中的所有样本做内积和即可。那有人会说,与前面所有的样本都做运算是不是太耗时了?其实不然,我们从KKT条件中得到,只有支持向量的![]() ,其他情况
,其他情况![]() 。因此,我们只需求新来的样本和支持向量的内积,然后运算即可。这种写法为下面要提到的核函数(kernel)做了很好的铺垫。
。因此,我们只需求新来的样本和支持向量的内积,然后运算即可。这种写法为下面要提到的核函数(kernel)做了很好的铺垫。
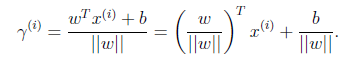
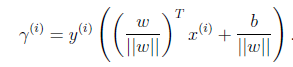
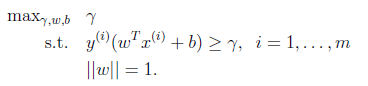
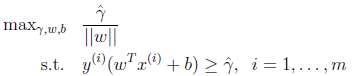
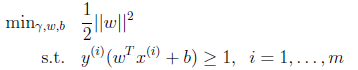
![clip_image008[6] clip_image008[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131234524417.png)
![clip_image078[6] clip_image078[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235401316.png)
![clip_image083[6] clip_image083[6]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103131235463131.jpg)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号