state space model -- kalman filter

最近学了金融计量，老师说Kalman Filter可以填充缺失值。一般我填充缺失值，赋值-1，或者让树模型自己填充缺失值，对于nn来说，要处理一下缺失值。

这些截图来自《银行家的计量书》，SSM可以提取时间序列中的结构性变化或者不可观测的成分，Dynamic Factor Models(DFM)也属于SSM的范畴，DFM中的共同因子属于不可观测的成分。
在很多参数的情况下，如果直接采用MLE的方法，会导致估计的无效性。我理解的是一般假定正太分布，我们可以求出一个L($\theta$), 然后去最大化似然函数，得到我们的参数，如果$\theta$的维度很高，这样会导致估计的无效。这时有没有什么解决办法？使用Gibbs采样（Gibbs采样是一种特殊的M-H算法），后面如果有时间写一个关于采样的帖子。

这里我有个疑问，如果说对于Nakajima（2011）的文章，MCMC的采样方法是由于MCMC的问题，还是由于对于SV采样的问题，Nakajima（2011）这篇文章相当于一个大综合，设计很多MCMC采样的思路。

一个常系数的SSM：一般包括连个方程，一个是观测方程，可观测的数据构成的方程，另外一个是转移方程，不可观测的成分构成的方程，一般是一个VAR(1)过程，如果系数是一个单位阵，那么转移方程是一个Random Walk(RW) Process, 这个也可以看作是一阶马尔可夫链，意味着当前之后一般仅仅与上一个时刻相关。
以前我会想我们假设的条件和现实总是格格不入，为什么还要使用这些假设。现在看来，这些假设基本是最简单、入门级别的，如果最基本的模型可以刻画出经济运行的状态，那说明这样还是很make sense的，每个模型都会有他的缺点，如果这个模型可以做出一些合理的解释，这已经是很不错了，我不要求有什么好的创新点，而且复杂的模型我也不懂呀。
这里我们对参数的假设是一个常系数协方差矩阵，并且两者是不相关的，后面估计会变成时变的，对于一个时刻，一个n维度的对称矩阵，如果要进行估计参数，要估计 $P_N= n(n+1)/2$ 个参数。

Example 1:

Example 2: 将一个时间序列数据降解成一个趋势成分和一个周期成分，一般来说 AR(2)模型可以描述周期性成分。

注意：如果状态变量是AR(p) process，那么 $\beta$将会有$p-1$个滞后阶，这也可以在Example中体现。

Example 3: Panel Data的动态因子模型， Kim的书有更多的例子。

Estimate

我们需要去计算哪些参数？观测方程：H、A、R，转移方程：$\mu$, F,Q; 状态变量 $\beta_t$。

对于常系数的SSM的估计，使用Gibbs 抽样一般是给定其他values，抽样此变量的后验分布，因此有时我们会看到可以写成一个新的状态空间模型：

这就涉及到状态变量的后验分布怎么求解？对所有时期（1，2,...T)的状态变量和观察数据进行Stacking，从T时候backward。

一直迭代就可以写成很长的样子：

一般我们假定状态变量是一个一阶马尔可夫过程：这样我可以对$\beta_{T}$, $\tilde{Y}_{T}$ 进行更新。

如果假定正态分布，可以得到下面这个表达式：那么怎么证明，这里给出了$\beta_{i|j}$的含义，在i时刻的评估，当信息更新到j时刻。

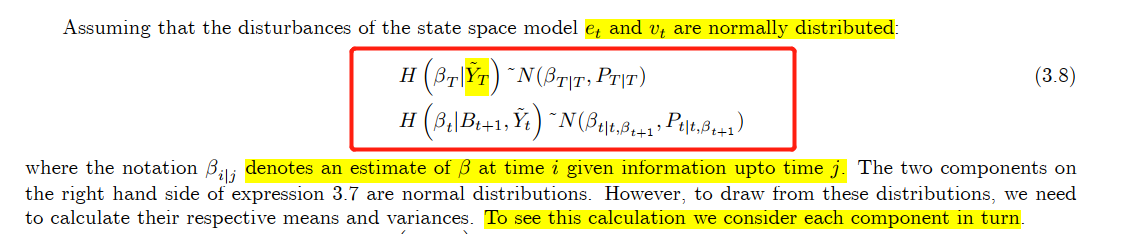
首先来计算 $H(\beta_{T}|\tilde{Y}_{T})$

具体指标的含义：

如何去解释这个投影，我们在OLS中也学过投影的含义，他是一个最好的预测。
我想基于Y1， Y2 预测 Y3，但我基于Y1对Y3的预测，基于Y1对于Y2的预测。可以基于投影的想法去建立联系，这是一个一般的形式，在这里我们把一阶马尔可夫过程或者SSM的约束加上，就可以得出Kalaman 更新步的两个方程。