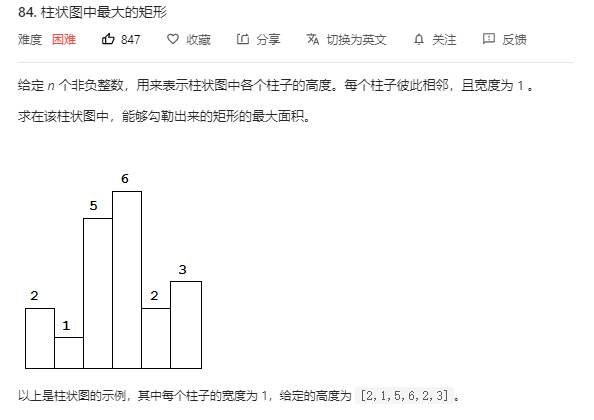
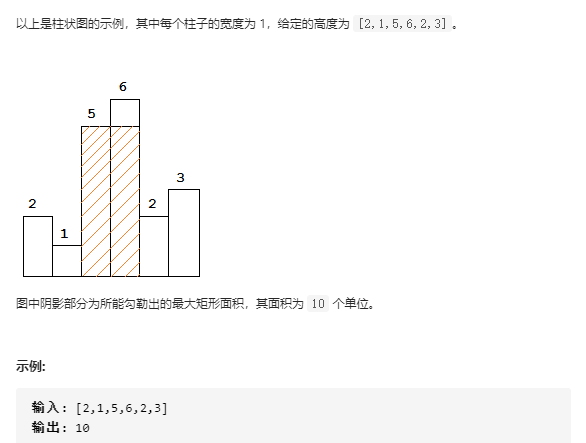
单调栈

 

 

 

 

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        if(heights.size()==0) return 0;

        stack<int>st;
        int res=-1;
        int len=heights.size();
        //遍历数组，将高度依次从小到大入栈（因为找最近的最小值）
        for( int i=0;i<len;i++ )
        {
            //如果栈不为空且入栈的数要比栈顶元素小或等于的话，就要出栈，一出栈就计算矩形的大小
            //矩形的长就是左边界和右边界的差值，左边界就是pop以后的栈顶的下标对应，右边界就是要入栈的下标
            //矩形的高就是弹出值下标对应的值
            while( !st.empty()&&heights[i]<=heights[st.top()] )
            {
                int h=heights[st.top()];
                st.pop();
                int l=st.empty() ? -1 : st.top();
                res= max( res,( i-l-1 )*h );
            }
            st.push( i );
        }
        while( !st.empty() )
        {
            int h=heights[st.top()];
            st.pop();
            int l=st.empty() ? -1: st.top();
            res= max( res,( len-l-1 )*h ); 
        }
        return res;
    }
};

　　

 

 

class Solution {
public:
    //每一行直接套用数组内求最大矩形
    int largestRectangleArea(vector<int> heights) {
        if(heights.size()==0) return 0;

        stack<int>st;
        int res=-1;
        int len=heights.size();
        //遍历数组，将高度依次从小到大入栈（因为找最近的最小值）
        for( int i=0;i<len;i++ )
        {
            //如果栈不为空且入栈的数要比栈顶元素小或等于的话，就要出栈，一出栈就计算矩形的大小
            //矩形的长就是左边界和右边界的差值，左边界就是pop以后的栈顶的下标对应，右边界就是要入栈的下标
            //矩形的高就是弹出值下标对应的值
            while( !st.empty()&&heights[i]<=heights[st.top()] )
            {
                int h=heights[st.top()];
                st.pop();
                int l=st.empty() ? -1 : st.top();
                res= max( res,( i-l-1 )*h );
            }
            st.push( i );
        }
        while( !st.empty() )
        {
            int h=heights[st.top()];
            st.pop();
            int l=st.empty() ? -1: st.top();
            res= max( res,( len-l-1 )*h ); 
        }
        return res;
    }
    
    int maximalRectangle(vector<vector<char>>& matrix) {
        if(matrix.size()==0||matrix[0].size()==0) return 0;
        vector<int>height(matrix[0].size(),0);
        int res=-1;
        //算出每行的直方图高度，如果这个单元格是1就让上面一个单元格的数值加一，不然就是0
        for( int i=0;i<matrix.size();i++ )
        {
            
            for( int j=0;j<matrix[0].size();j++ )
            {
                height[j]= matrix[i][j]=='1'? height[j]+1 : 0;    
            }
            res=max( res,largestRectangleArea(height) );
        }

        return res;
    }

};