AGC 069

C. AB*A Changing

从左到右扫描序列，把每次操作的线段看作左边加入/右边删除，记录经过当前位置的线段数量。

在每个位置会有若干条线段开始（操作 \(A\to B\)），若干条线段结束（操作 \(A\to B\)），有若干条线段经过（操作 \(B\to A\)）。

考虑 DP，设 \(f(i,j)\) 表示扫到第 \(i\) 个位置，往后还有 \(j\) 条线段没结束。转移时枚举一下删除/加入的线段数量，并且要满足 \(s_i\) 变化的要求（如 \(A\to B\to A\to \cdots\to B\) ）。

然后由于一些不知道什么原因，DP 的第二维只需要开一个很小的常数就对了（credit from noshi91，proof by AC，我不会证），实际上只需要开到 \(4\)。

时间复杂度 \(O(n)\)。

int n;
char s[maxn],t[maxn];
int f[maxn][13];
void work()
{
	n=read(),scanf("%s%s",s+1,t+1);
	memset(f[0],63,sizeof f[0]);
	f[0][0]=0;
	int B=4;
	For(i,1,n){
		memset(f[i],63,sizeof f[i]);
		int now=(s[i]=='B');
		int nd=(t[i]=='B');
		int c01=0,c10=0;
		For(j,0,B){
			if(now==nd){
				For(k,0,B){
					int x=k-c10;
					if(x>=0 && x<=c01){
						int t=(k-x)+(c01-x);
						if(t>=0 && t<=B)
							f[i][t]=min(f[i][t],f[i-1][k]+(c01-x));
					}
				}
			}
			if(now==0)++c01;
			else ++c10;
			now^=1;
		}
	}
	if(f[n][0]<inf)cout<<f[n][0]<<"\n";
	else puts("-1");
}

D. Tree and Intervals

感觉这个题可做啊，真该先开这个题的/fn

\(x_i\) 可以看作一端 \(\le i\)，另一端 \(>i\) 的边数，进一步可以转化为：把 \(\le i\) 的点染成黑色，\(>i\) 的点染成白色，得到的总连通块数。

考虑判定怎样的“总连通块数”序列是可以被生成的。

一个个把点染黑，维护当前的黑色连通块数 / 总连通块数。

如果某一步总连通块数不变，那这步可以忽略。

如果某一步总连通块数增大，那黑色连通块数可能 \(+0\) 或 \(+1\)（如下图）。

如果某一步总连通块数减小，那黑色连通块数需要减小，有两种减小方式（如下图）：

• 第一种方式：总连通块数 \(-cnt\)，黑色连通块数 \(-cnt\)。
• 第二种方式：总连通块数 \(-(cnt+1)\)，黑色连通块数 \(-cnt\)，此时要保证有 \(\ge 2\) 个白色连通块（否则所有白色都消失了），或者这是最后一次操作。

最后操作完要保证黑色连通块数 \(\ge 1\)。

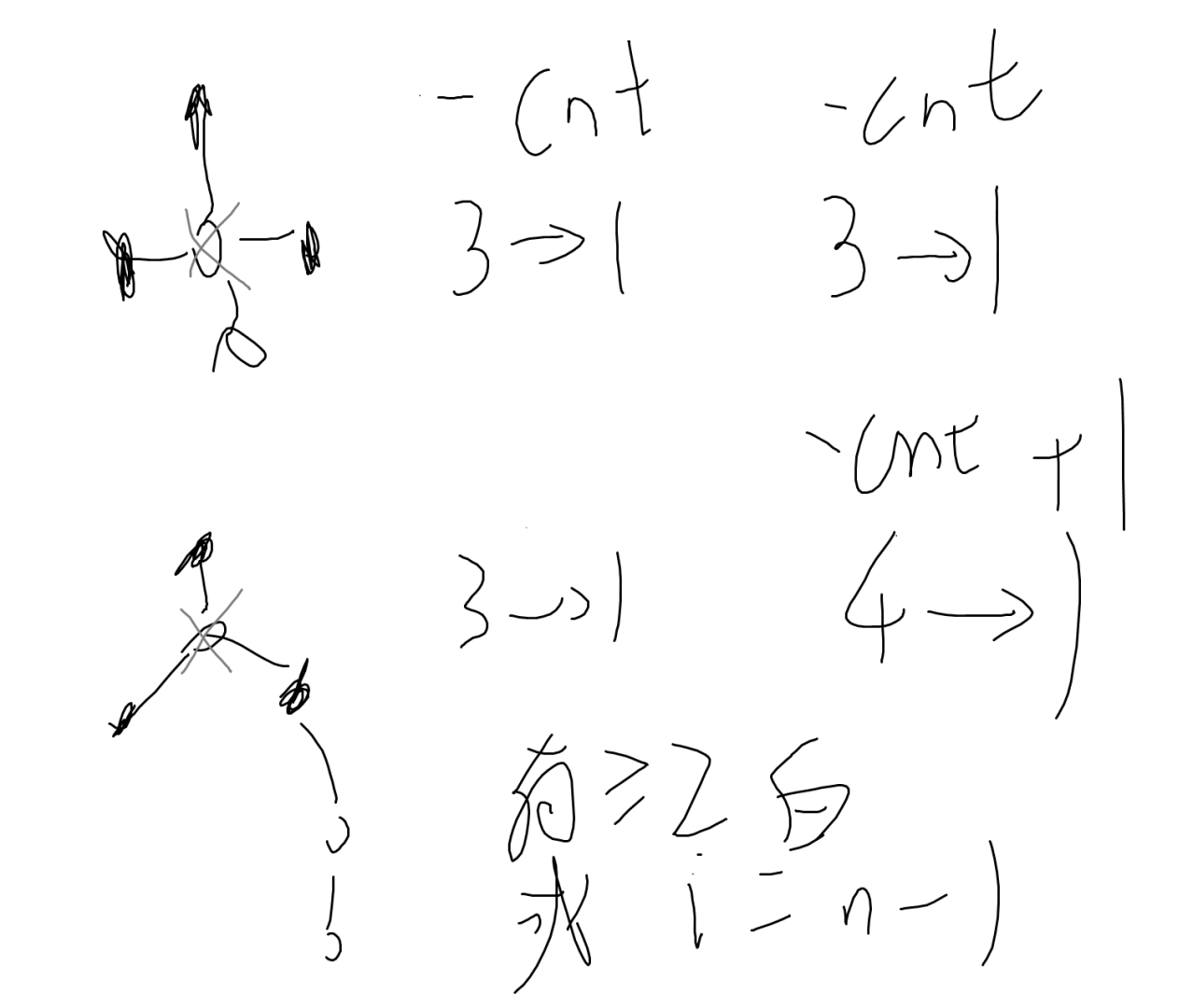
显然黑色连通块数越多越好，这样可以保证不被减到 \(\le 0\)。

我们可以贪心，维护当前能达到的最大黑色连通块数。由于第二种方式比第一种减少的更少，如果能用第二种方式就用第二种，否则用第一种。

设 \(f(i,j,s)\) 表示黑色连通块数为 \(j\)，当前总连通块数为 \(s\) （这也确定了白色连通块的个数 \(=s-j\)）的方案数，其中 \(j\) 这一维贪心计算。

枚举到下一个位置的连通块变化数，据此可以写出 \(O(n^4)\) 的转移：

int n;
modint f[505][505][505];
signed main()
{
	n=read(),initmod();
	For(i,2,n) f[1][1][i]=1;
	For(i,1,n-1){
		For(j,1,n) For(s,1,n) if(f[i][j][s].x) {
			int wh=s-j;
			For(k,1,n) if(s+k<=n) f[i+1][j+1][s+k]+=f[i][j][s];
			f[i+1][j][s]+=f[i][j][s];
			For(k,1,n) {
				int jj=j-(k-1)-(wh<=1 && i<n-1);
				if(jj>=1 && jj<=n && s-k>=1) f[i+1][jj][s-k]+=f[i][j][s];
			}
		}
	}
	modint res=0;
	For(j,1,n)res+=f[n][j][1];
	cout<<res.x;
	return 0;
}

发现转移可以前缀和优化到 \(O(n^3)\)，就做完了。submission

E. Pair of Sequences

列出答案的生成函数。

\[[x^ny^Sz^T] \prod_{i=0}^{m-1}(1+\sum_{j\ge 0} x y^i z^{ij}) \]

\[=[x^ny^Sz^T] \prod_{i=0}^{m-1}(1+\frac{x}{1-yz^i}) \]

\[=[x^ny^Sz^T] \prod_{i=0}^{m-1}\frac{x+1-yz^i}{1-yz^i} \]

---

拆开分子与分母，两部分都是 q-binomial 的形式。

分子：

\[\prod_{i=0}^{n-1} (1+q^iy) = \sum_{i=0}^n q^{\binom{i}{2}} {n \brack i}_q y^i \]

\[\prod_{i=0}^{m-1}(x+1-yz^i) \]

\[=(x+1)^{m} \prod_{i=0}^{m-1} (1-\frac{y}{x+1}z^i) \]

\[=(x+1)^{m}\sum_{i=0}^m z^{\binom{i}{2}} {m\brack i}_z (- \frac{y}{x+1})^i \]

\[=\sum_{i=0}^m (x+1)^{m-i} (-1)^i z^{\binom{i}{2}} {m\brack i}_z y^i \]

---

分母：

\[\frac{1}{\prod_{i=0}^{n} (1-q^ix)} = \sum\limits_{i \ge 0} x^i {i+n \brack n}_q \]

\[\frac{1}{\prod_{i=0}^{m-1} (1-yz^i)} \]

\[=\sum_{i\ge 0} {i+m-1 \brack m-1}_z y^i \]

---

一边提取 \([y^i]\) 系数，一边提取 \([y^{S-i}]\) 系数。

\[=[x^nz^T]\sum_{i\ge 0} (x+1)^{m-i}(-1)^i z^{\binom{i}{2}} {m\brack i}_z {S-i+m-1 \brack m-1}_z \]

\[=[z^T]\sum_{i\ge 0}\binom{m-i}{n}(-1)^i z^{\binom{i}{2}} {m\brack i}_z {S-i+m-1 \brack m-1}_z \]

由于 \(z^{\binom{i}{2}}\) 的存在，需要保证 \(\binom{i}{2}\le T\)，\(i\) 只能枚举到 \(O(\sqrt T)\) 大小。

从小到大枚举 \(i\) 并暴力维护右边关于 \(z\) 的多项式即可，每次只需要做若干次形如 \(z^k-1\) 的乘/除。这部分复杂度 \(O(n\sqrt n)\)（设 \(n,m,S,T\) 同阶）。

当 \(i=0\) 时多项式为 \({S+m-1 \brack m-1}_z\)，可以 \(O(n\log n)\) 算出（多项式 ln/exp）。