2023 暑假 正睿笔记
Day 1
"基础"数据结构
并查集
每次合并集合, 就在两个点之间连上边, 询问就是看两个点是否在同一连通块
但是朴素的并查集复杂度没有保证
所以考虑优化
路径压缩
改变树的结构不会改变它的连通性
我们考虑为什么我们之前复杂度会退化
很重要一个原因就是有可能路径太长
所以我们把路径压缩了不就行了
int find (int x) {
if (fa[x] == x) return x;
else return fa[x] = find(fa[x]);
}
按秩合并
就是按照树的大小, 进行合并
这样技能尽可能的保证树不会退化成链
void merge (int x, int y) {
if (siz[x] < siz[y]) swap (x, y)
siz[x] += siz[y];
fa[y] = x;
}
hyt大佬的奇怪技巧
随机化
void merge (int x, int y) {
if (rand() & 1) fa[x] = y;
else fa[y] = x;
}
hyt你差不多得了, 别再随机化了
再随机化给你 #define sort random_shuffle
例
相等操作可以传递, 不等操作不可以传递
然后离线先处理相等再处理不等
显然不是很好
并查集撤销
需要按秩合并, 因为路径压缩复杂度无法保证
然后按秩合并时, 只需要记下来改了什么, 改回去就行
Kruskal 重构树
怎么建kruskal重构树呢?
我们发现, 在做kruskal时会先进行排序, 那么最小生成树加入边的边权一定是从小到大的
那么如果我们知道了两点之间最后加的边, 就求出了两点之间路径的最大值
那么考虑把每个边断开, 对加入的每条边都新建一个节点, 点权等于边权, 刚才的问题就转化为了两个点之间最后加的点的点权
所以考虑把边权转为点权后, 每次并查集合并把新建的点作为根, 维护连通性
然后直接在并查集建的树(kruskal重构树)上求lca, lca的点权就是我们要两点间路径最大的
倍增
树上倍增
LCA
例:
可持久化并查集?
ST表
就是把一个i, j的区间最小值转化为两个长为 2 ^ j 的区间的最小值
大例题
不会, 摆烂
树状数组
核心就是一个 \(lowbit\)
然后直接上代码
inline int lowbit (int x)
{
return x & (-x);
}
int t[maxn];
inline int add (int pos, int x)
{
for (int i = pos; i <= n; i+= lowbit(i)) res += t[i];
}
inline int sum (int pos)
{
int res = 0;
for (int i = pos; i; i -= lowbit(i)) res += t[i];
return res;
}
关于lowbit怎么算:
显然
x & (-x)但怎么证明呢?
\(x\) 第一个 \(1\) 后面显然原来都是 \(0\) 取反以后显然都变成 \(1\), 第一个 \(1\) 变成了 \(0\)
再加上 \(1\) 以后第一个 \(1\) 后面显然都变成了 \(0\), 原来第一个 \(1\) 的位置上又有了一个 \(1\) (进位)
然后前面的数都是取反过后的
与上 \(x\) 显然都是 \(0\)
至此, 除了原来第一个 \(1\) 的位置上有 \(1\) , 其他都是 \(0\)
树状数组上的二分
不会, 摆烂
喜报, 会了
先放例题
首先自然是要对 \(x\) 离散化的
显然, 当 \(t\) 增加时, 左边增大, 右边减小, 并且具有单调性
所以我们先考虑画个图
大概就是两条线组成了一个 X
显然, 最小值最大时, t应该是在 X 的中间交叉的那个点
于是我们可以尝试二分出交叉的点
怎么二分呢?
用树状数组维护左边的线的前缀和 和 右边的线的后缀和
然后进行二分找出最优解
这样喜提 70pts
所以考虑优化复杂度
我们发现, 树状数组本身就是类似于倍增的一个数据结构
我们直接通过不停跳lowbit也能实现二分
upd at 2024.1.29 : 终于过了冰火战士
这种其实已经不能叫做二分了, 应该叫倍增
线段树
又臭又长
但真的好用
打Tag的技巧
只有区间加
直接记下来就好了
只有区间乘
也直接记下来就好了
又有区间加又有区间乘
也直接记下来就好了
但是我们发现, 加和乘的优先级是不一样的
也就是说, 应该先乘后加, 从左到右计算
所以维护两个 \(tag\), 一个是 \(tag1\) (维护乘), 另一个是 \(tag2\) (维护加)
于是加的时候, 直接加到 \(tag2\)
乘的时候, \(tag1\) 和 \(tag2\) 都应该被乘
下传标记时, 先传 \(tag1\) 再传 \(tag2\)
区间开根
我的评价是寄
二维扫描线
用线段树来维护扫描线即可
题
Envy
奇妙的最小生成树题
首先, 我们应该知道同一个图的最小生成树都有哪些性质:
对于同一个图的最小生成树
-
它相同权值的边的数量是一定的
-
而且如果设当前边的边权为 \(w_i\) , 必须先尝试把所有 \(w_j < w_i\) 的边加入树中
为什么呢?
因为这些边中的一些如果不加入最小生成树, 可能会使答案劣化, 所以必须尝试加入
而且, 一组询问中, 各种边之间是不影响的, 我们只需要按照 \(w\) 从小到大的进行处理即可
那么处理起来是不难的, 离线后对边进行排序后再处理即可
总结起来就是离线, 排序, 然后按顺序尝试加边, 如果有多个 \(w\) 相等, 那我们必须尝试把他们全部加进去, 如果加不进去, 答案自然就是不可能的
但是, 这题有多组询问 !
怎么办呢?
-
有一种很容易想出来的方法是可撤销并查集
每次把之前加入的边撤销
但是, 这样有一点难写
所以我们直接
开摆不写搞出了一个更好的方法 -
我们发现, 我们想要知道的是 \(w\) 比当前边小的点, 它们的连边情况是怎样的
那么, 为什么不先按照 \(w\) 从小到大跑一遍 \(Kruskal\) , 预处理出它们的连边情况并且记录下来
然后, 在查询的时候, 直接就能知道之前的连边情况是怎样的
然后对于每次查询结束的时候, 我们在把这个并查集复原就行
怎么复原? 就是把每个这个过程中改过的点再把它改成原来我们并查集初始化时它的编号
Day 2 - 线段树
小白逛公园
线段树打标记技巧
怎么打呢?
首先我们考虑一个区间最大字段和是怎样求出来的, 怎样能够合并
我们首先把区间分为两部分: \([l, mid]\) 和 \([mid + 1, r]\) (跟线段树一样)
容易想到, 有三种情况:
-
这个最大子段在左边的区间 \([l, mid]\) , 所以我们需要维护每个区间的最大字段和
-
这个最大子段在右边的区间 \([mid + 1, r]\) , 所以我们也需要维护每个区间的最大子段和 (与第一种情况同理)
-
这个最大子段跨两个区间, 那么我们发现, 这个子段一定是由左边的区间的一个后缀和右边的区间的一个前缀组成的
那么, 最大字段和一定是由左区间的最大后缀和右区间的最大前缀组成的
综上, 我们发现, 对于每个区间, 我们一共需要维护的东西是: 最大子段和, 最大前缀, 最大后缀
然后考虑怎么合并:
-
对于最大前缀, 我们考虑求 左边区间的最大前缀 与 左边区间的和加上右边区间的最大前缀 的最大值
-
对于最大后缀, 我们考虑求 右边区间的最大后缀 与 右边区间的和加上左边区间的最大后缀 的最大值
-
对于最大子段和, 我们考虑求 左边区间的最大后缀加上右边区间的最大前缀 与 左右两边的最大子段和
斐波那契数列
线段树打标记技巧
斐波那契数列是有通项公式的
然后发现这里面的有两项是可维护的 ( \((\frac{1 + \sqrt 5}{2}) ^ n\) 和 \((\frac{1 - \sqrt 5}{2}) ^ n\) )
我们把它们记为 \(p ^ n\) 和 \(q ^ n\)
然后我们考虑怎么维护 \(p\) 和 \(q\)
我们发现我们可以用两棵线段树分别维护 \(p\) 和 \(q\)
这样我们就能快速的把通项公式代入进行计算了
不过, 我们发现, 这里面的 \(\sqrt{5}\) , 不是很适合我们处理
然而我们又发现, 答案其实是要模上一个大数 \(1e9 + 9\)
那我们考虑, 能不能在模意义下找到一个数来代替 \(\sqrt{5}\) 呢
首先自然能想到一个很暴力的方法来寻找这个数
因为模数是固定的, 直接从 \(1\) 跑到 \(1e9 + 9\) 来寻找一个数平方以后模 \(1e9 + 9\) 为5
但是这样的方法不是很优雅, 肯定有别的方法
所以我们发现, 如果我们用一个结构体来记录每个数的有理数和无理数部分, 这些运算是封闭的, 也就是说, 无理数一定能够被约掉
为什么呢?
一个很显然的证明是斐波那契数列的每一项 (通项公式计算出来的值) 都是整数, 不会有无理数部分
等差子序列
动态图连通性
线段树套并查集
首先看到求连通块个数, 这显然可以用 \(bfs\) 搜索
一看数据范围 题目难度, 复杂度必然爆炸 ( \(O(Qn ^ 2)\) )
所以尝试使用一些更好的方法来统计连通块个数
再次考虑我们要求的是什么? 是连通块的个数
那有什么奇妙的数据结构能帮我们呢?
自然是并查集啊
但是我们发现, 这复杂度不降反增, 每次加入还多了个 \(\log n\)
显然不是很好
但是并查集有什么特点?
很容易合并 废话, 它叫并查集啊
所以我们考虑, 怎么样利用这种可合并特性
于是, 我们想到了线段树
线段树的每个操作都需要合并
那么具体怎么做呢?
先考虑只有一行的情况
1100011
1表示黑色, 0表示白色
显然可以对这一行做并查集, 我们发现我们能够很容易知道这一行都有多少白色连通块和多少黑色连通块 (直接并查集即可)
那我们现在再来考虑两行的情况
1100011
1000101
那么我们也很容易知道下面一行有多少白色连通块和黑色连通块
所以考虑怎么把两行合并
我们先初始答案为两行联通块的数量加起来
显然, 如果同一列中上下两行的颜色相等, 那么, 它们就在同一个连通块中, 所以答案必须 \(-1\) , 要不然本来是一个连通块的两个点就被算了两遍, 答案会比真正的答案大 \(1\)
所以我们不断合并即可, 用线段树来维护这些并查集
然后, 我们发现我们正好收获了一个很好的性质, 就是这些被线段树维护的并查集支持修改
所以我们每次单点修改的时候, 就在线段树上进行单点修改即可
线段树打标记
单点修改 + 区间取模 + 区间和
区间加 + 区间开根
一个显然的操作是维护一个加法的懒标记
但是这只能解决区间加法
线段树合并
什么是线段是合并?
就是把两棵线段树合并起来 这不废话么
先看道例题
一个显然的做法是树上差分
但是我们发现这东西有好多种类
所以, 并不能只用一个数来统计当前节点的差分
最好再开一个桶, 维护每种物资的数量
然后, 我们考虑差分以后如何统计答案
显然是要把这些差分桶加起来
但是又有一个很显然的问题是, 我们怎么样去加这些桶呢?
如果暴力加显然复杂度也爆炸
于是考虑使用数据结构维护
所以我们想到了值域线段树, 因为它本质就是一个用线段树维护的桶
那么想到了线段树, 我们就几乎做出了这道题的正解
因为我们知道, 线段树其实是可以合并的, 而且, 有一个专门的算法:
-
对于每个不存在的点, 自然需要把它直接赋为另一棵树上存在的点
-
对于每个叶子节点, 显然的做法是把他直接加上另一棵树的叶子节点
-
那么对于每个非叶子节点, 我们可以把它们的左子树递归合并, 然后右子树也递归合并, 最后
push_up更新当前的点
李超线段树
咕咕咕
Day 3 - 分块
分块 = 多叉线段树
广义上的分块思想实际上是设定一个阈值 \(B\), 然后把问题分成 \(B\) 和 \(n / B\) 两部分
为了寻求两部分时间复杂度的平衡, 我们常常把 \(\sqrt{n}\) 设置为阈值
区间加 + 区间求和
很容易的打懒标记
区间加 + 单点查询
离线
显然维护懒标记就行了
Tree master
树上分块?
实际上是暴力
我们先考虑怎么写暴力
很显然, 题目中已经给出了一个不断往上跳的递推公式
我们考虑 \(dfs\) 直接把他求出来
但这样显然复杂度爆炸
那么考虑优化:
-
一个显然的优化是: 如果两个点不停的向上跳, 跳到了它们的 \(lca\) , 然后剩下的向根节点 \(1\) 跳的路径的贡献显然是他们路径上经过的点的权值的平方和
那么我们考虑把根节点到任意点的平方和预处理出来 ( 因为每个点都有可能成为 \(lca\) )
-
考虑记忆化搜索优化:
记忆化搜索实际上需要我们每次记下来答案, 但是很显然的一个不足的点是 \(n \le 10 ^ 5\) , 没有那么多空间给我们存
所以考虑分块
我们把整个问题分成两部分, 把阈值 \(B\) 设为 \(\sqrt{n}\) , 先把树按深度分层, 对于每个点数小于等于阈值 \(B\) 的层, 我们尝试对它进行记忆化, 其他的层暴力 \(dfs\)
交上去居然 AC 了, 跑的飞快
然后考虑一下复杂度:
-
对于我们记忆化的层 (点数 \(x \leq \sqrt{n}\) 的层), 最坏情况下, \(dfs\) 函数会被调用 \(x ^ 2\) 次 ( 因为任意两个点 \(x\) 和 \(y\) 可以被放在 \(dfs(x, y)\) 中, 并且不会多次调用 )
然后, 最多会有 \(n / x\) 个这样的层
所以我们计算一下这部分的复杂度, 就是 \(O(n / x * x ^ 2) = O(n * x) \leq O(n * \sqrt{n})\)
-
对于其他的层, 节点数 \(x \geq \sqrt{n}\) 我们可以知道这样的层数量一定小于 \(\sqrt{n}\), 那么考虑询问 \(q\) 次, 那么这些层中 \(dfs(x, y)\) 最多被调用 \(q\) 次
然后我们就能知道这部分的复杂度是 \(O (q * \sqrt{n})\)
因此, 总体复杂度就是 \(O (n * \sqrt{n} + q * \sqrt{n})\) , 并且其中\(n \leq 10 ^ 5, q \leq 10^5\)
总体复杂度正确
区间众数 (强制在线)
分块大法好
用分块维护两个数组:
-
p[i][j]表示第 \(i\) 块到第 \(j\) 块的众数 -
s[i][j]表示前 \(i\) 块中 \(j\) 出现的次数
这两个数组预处理出来就行
那么怎样使用呢?
显然是整块预处理, 散块暴力
那么考虑每次新添一个散块中的点如何更新
一个显然的方法是, ++ 当前数的出现次数, 如果这个数的出现次数大于当前众数的出现次数, 那么显然这个数就成为了新的众数
需要注意的一点是, 散块内的数的出现次数要加上它们在整块中出现的次数
而且, 整块内众数出现次数需要单独加 (因为有可能整块中的那个众数不在散块中出现)
因为其实有可能整块中原本不是众数的数, 加上它在散块中出现的次数, 就成为了众数
于是就可以愉快的 TLE 了
不要乱用memset!!!
被卡常了就难绷
因为被卡常调了114514年啊啊啊啊
Day 4
平衡树
BST (二叉搜索树)
普通BST还是很容易维护各种信息的
因为它具有 \(BST\) 所有优秀的性质
于是我们的任何操作都只要递归的从上往下跑, 每次选择左子树或右子树进行递归即可
在数据随机情况下, \(BST\) 期望是平衡的, 但是可以构造数据把 \(BST\) 卡成链, 单次操作可能到 \(O(n)\)
Treap
数据随机的情况下, \(BST\) 的复杂度是良好的, 但是数据不一定随机
所以, 我们的 \(Treap\) 让每个点有一个随机键值, 使得光看键值, 是一个堆; 光看数值, 是一棵 \(BST\)
FHQ-Treap
怎么突然上难度了
不过 \(FHQ-Treap\) 其实不难
主要就是分裂与合并
之前 hyt 大佬教过我
代码里有详细的注释, 直接看代码吧
struct Node {
int l, r;
int val, key, size;
};
Node fhq[maxn];
int cnt, root;
inline int newNode (int val) {
cnt ++;
fhq[cnt].val = val;
fhq[cnt].key = rand();
fhq[cnt].size = 1;
return cnt;
}
inline void update (int x) {
fhq[x].size = fhq[fhq[x].l].size + fhq[fhq[x].r].size + 1;
}
void split (int now, int val, int& x, int& y) { // x <= val y > val
if (not now) {
x = y = 0;
} else if (fhq[now].val > val) {
y = now; // now 和 它的右子树都一定 > val
split (fhq[now].l, val, x, fhq[now].l); // 左小右大
update (now);
} else {
x = now; // now 和 它的左子树都一定 <= val
split (fhq[now].r, val, fhq[now].r, y); // 左小右大
update (now);
}
}
int merge (int x, int y) { // 把 y 合并到 x 上 (x 小 y 大)
if (not x or not y) {
return x | y; // 有一个是零, 因此加/或起来的一定是那个不为0的
} else if (fhq[x].key < fhq[y].key) { // 考虑维护key是堆的性质
fhq[x].r = merge (fhq[x].r, y); // x 放在上面
update (x);
return x;
} else {
fhq[y].l = merge (x, fhq[y].l); // y 放在上面
update (y);
return y;
}
}
inline void insert (int val) {
int x, y;
split (root, val, x, y); // x: <= val
x = merge (x, newNode(val));
root = merge (x, y);
}
inline void remove (int val) {
int x, y, z;
split (root, val, x, y); // x <= val, y > val
split (x, val - 1, x, z); // x < val, z > val - 1 => z >= val => z = val (因为x <= val, 以x为根的子树中所有点都 <= val)
z = merge (fhq[z].l, fhq[z].r); // 把z的两个儿子合并起来 (相当于z (=val) 的都没了)
root = merge (merge (x, z), y); // 把散着的树都合并起来
}
inline int pre (int val) {
int x, y;
split (root, val - 1, x, y);
int now = x; // 小于 val
while (fhq[now].r) {now = fhq[now].r;} // 中最大的
root = merge (x, y);
return fhq[now].val;
}
inline int nxt (int val) {
int x, y;
split (root, val, x, y);
int now = y; // 大于 val
while (fhq[now].l) {now = fhq[now].l;} // 中最小的
root = merge (x, y);
return fhq[now].val;
}
inline int get_rank (int val) {
int x, y;
split (root, val - 1, x, y); // 比 val 的数
int rank = fhq[x].size + 1;
merge (x, y);
return rank;
}
inline int get_num (int rank) {
int now = root;
while (now) {
if (fhq[fhq[now].l].size + 1 == rank) {return fhq[now].val;}
else if (fhq[fhq[now].l].size >= rank) {now = fhq[now].l;}
else {rank -= fhq[fhq[now].l].size + 1; now = fhq[now].r;}
}
return -1; // 不存在
}
Splay
\(Splay\) 就是一棵普通的 \(BST\), 每次插入/查找都先把要操作的点转到根
(于是这样就似乎可以证明是卡不掉 \(Splay\) 的)
先令每个点都存三个点的下标 (lc, rc, fa)
然后考虑怎么旋转:
(假设x要旋到y位置上, x左儿子为A, 右儿子为B, y右儿子为C)
旋转
普通旋转是不难的
不断的把当前节点往上旋转即可
三点共线
什么是三点共线的情况呢?
像这样
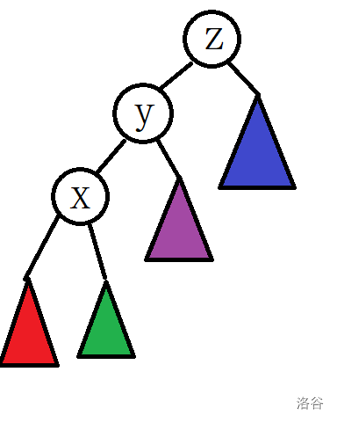
或这样
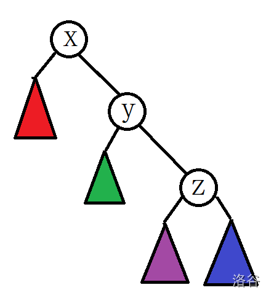
的就是三点共线
图怎么挂了
Day 5
可持久化数据结构
可持久化值域线段树
例1 区间 \(k\) 小
题目大意
给定一个序列, 求区间 \(k\) 小值
Solution
首先考虑求第 \(k\) 小的值, 我们可以把它转化为维护和的值域线段树上的二分
值域线段树实际上是用线段树维护了一个桶
因此值域线段树上求和就相当于看当前值域有多少个数
我们考虑如果有一个数恰好有 \(k\) 个数比它小, 显然这个数就是第 \(k\) 小, 因此我们考虑值域线段树上的二分
但至此, 我们只完成了第 \(k\) 小, 并没有完成 "区间" 这个性质
那么, 我们考虑我们是怎么加点的, 我们一定是从前往后加的, 因此我们目前求出的是前缀 \(k\) 小
那怎样完成前缀到区间的转化呢?
一个显然的方法是维护历史版本, 找到之前的取值
例如, 我们要求 \([l, r]\) 的 \(k\) 小, 我们把 \([1, l]\) 中加入的点的贡献减掉以后, 再在线段树上进行查找即可
例2 树上路径 \(k\) 小
考虑树剖
然后就转化为了线段树上的二分
可持久化并查集
注意不能使用路径压缩, 必须按秩合并
左偏树
Day 6
虚树
引入
我们发现并不是所有点都可能对答案产生贡献, 有些点对答案不会产生贡献
那么, 一个显然的做法是把那些不会对答案产生贡献的点删掉
但是, 删掉以后可能产生的一种问题就是, 树的结构可能不复存在, 甚至一棵树都不连通了
定义
于是我们考虑如何维护这些点的连通性
所以, 对于每两个点, 我们把它们和它们的 \(lca\) 加入这棵新的树
这颗新的树, 就叫虚树
这样, 在虚树中再进行操作, 就能够最小化我们的操作复杂度 (没有用的点都不在虚树中了)
构建
但是, 我们发现, 我们在定义中给出的建树方法, 似乎是 \(O(n ^ 2)\) 的
那建虚树岂不是比不建还要慢
所以我们考虑怎么样快速的构建虚树
二次排序
点
假如, 我们把每个点的\(dfs\) 序 ( \(dfn\) ) 都记录下来
那么有一个显然的结论是, \(dfs\) 序相邻的点, 它们之间的简单路径上并不会再有其他点
所以我们考虑, 我们要插入到的虚树中的点都有什么:
首先根据定义, 我们知道任意两个点和它们的 \(lca\) , 都必须在虚树里
但真的有那么多点吗?
我们刚才推出结论, 任意两个 \(dfs\) 序相邻的点, 它们的简单路径上都不会再有其他的点
所以, 我们其实只需要加入任意两个 \(dfs\) 序相邻的点的 \(lca\) 就行了
那加点的操作就很简单了, 我们一遍 \(dfs\) 求出所有点的 \(dfs\) 序
然后把这些点按 \(dfs\) 序排序, 再把相邻的两个点的 \(lca\) 加入点集
那么, 我们现在就知道了到底有哪些点需要被加入虚树中
边
但是, 我们又考虑到, 虚树中不只有点, 我们刚才只知道了 那些点要被加入, 所以, 我们考虑的重点变为了怎样连边
其实也很简单
根据刚才我们推出来的结论, 如果两个关键点的 \(dfs\) 序是相邻的, 它们中间就不会有别的点
然后, 我们又发现, 我们其实已经知道了有哪些点要被加入虚树以及它们的 \(dfs\) 序 ( \(lca\) 的 \(dfs\) 序也会被一开始的那遍 \(dfs\) 求出来了), 而且, 两个点之间能够连边, 当且仅当它们之间没有别的点 (如果有别的点, 那就向那个点连边了)
于是, 我们只需要对所有需要插叙虚树中的点(包括关键点的 \(lca\) ), 按照 \(dfs\) 序再排一次序就行了
然后, 相邻的两个点进行连边
单调栈
不是很会, 摆烂
线段树分治
实际上就是在可撤销线段树上进行dfs
例题
题意
每个物品出现时刻为一个区间。有一个栈,可以在末尾加删物品。需要对于每个时刻,都存在某个时刻的栈,物品集合为该时刻出现的所有物品。
Solution
首先考虑直接模拟, 考虑每个物品每次开始出现的时候把它加进栈中, 每次结束出现的时候删掉它
但是, 我们发现栈不能在里面删除元素, 于是就寄掉了
但是我们发现
如果我们把栈中每个元素放在一棵值域线段树上, 我们就能很方便的表示出一个值的开始和结束
而且, 线段树支持撤销
于是我们每次当一个值从栈的最后弹出, 撤销一下这颗线段树即可
然后我们考虑在线段树上 \(dfs\) , 每次一个值出现时间结束以后, 自然而然的就被删除了
长链剖分
其实就是一种树链剖分
跟轻重链剖分是很像的
直接上例题
例: \(k\) 级祖先
我们考虑, 维护长链
类比轻重链剖分, 我们把每一个点的儿子中深度最大的叫做 "长儿子"
然后我们考虑维护这条链上的各种信息(如某个深度对应的点)
然后再倍增维护一个当前节的 \(2 ^ i\) 级祖先是多少
然后我们可以往上跳到小于 \(k\) 的 \(2 ^ i\) 级祖先
这样我们发现, 现在跳到的这个点, 离我们的 \(k\) 级祖先的距离一定是小于当前长链的长度
所以我们跳到当前链的顶端
于是我们发现我们可以 \(\mathcal O(1)\) 的查询 \(k\) 级祖先 (因为我们已经提前维护好了这条长链中的深度对应的点)
Day 7
膜你赛
A题
诈骗题!!!
然后我还被诈骗了
然后还用了常数上天的 \(set\)
然后还没写快读
综上, 我又被卡复杂度又被卡常
然后喜提 30pts 挂大分!
然后其实A题是有一定的思维含量的 像我这样只会基础语法的滚去Z班
B题
考虑我们实际上是要维护最大子段和
那么首先考虑一维的最大子段和如何维护
我们都知道可以直接dp, 然后求出最大子段和
但是我们发现, 要维护的并不是一维的最大子段和, 题中要求是二维
所以考虑怎样从一维转化为二维
首先我们可以想到找一条扫描线, 从下往上扫, 每次把扫到的点用来更新当前的最大子段和
这看起来确实十分美好
于是这就是动态dp的板子 然而我不会动态dp
但又没有更容易的方法呢?
我们想到, 我们之前做过一个题: "小白逛公园", 我们用线段树维护了区间的最大子段和
线段树!
我们有考虑到, 线段树 支持更新 !
那么, 事情就变简单了, 我们考虑用线段树来维护最大子段和 (即要维护前缀最大和, 后缀最大和, 区间最大子段和)
然后每次扫描线扫到一个新的点, 我们考虑把它加入到线段树中 (单点修改即可)
然后每次扫描线移动之前, 用整个区间 (1 ~ n) 的最大子段和更新一下答案
Day 8
终于开始DP 毒瘤数据结构终于结束了
虽然我DP也超弱的
区间DP
区间DP的标志是一个大的区间的答案可以由几个小的区间转移过来 / 大区间可以分裂成小区间
做此类题目要敏锐观察题目中的条件并设计合适合理的状态,看看能否从小状态推至大状态,先通过这个写出暴力dp方程,然后再尝试求解。
~~膜拜大佬@cunzai_zsy0531 ~~
板子:
/* 注意:
* 一般的题初始化的过程中会初始化长为1的情况 (dp[i][i]),
* 所以len要从2开始 (有时候从3开始)
*/
for (int len = 2; len <= n; len ++) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1; // 上面的l + len - 1 <= n 就是r <= n
for (int k = l; k < r; k++) {
/*
* 分成 [l, k], [k + 1, r] 两部分 (所以k要小于r)
* 然后进行dp
*/
}
}
}
区间dp, 实际上就是考虑如何从小区间转移到大区间, 然后答案就是整个区间
ZUMA
这应该是区间dp最经典的题了
题意
每次可以删除一个回文串, 求删除整个序列的最小操作次数
Solution
首先我们考虑, 一个回文串是如何出现的
假设目前有一个区间 \([l, r]\) , 如果 \(a_{l - 1}\) 等于 \(a_{r + 1}\)
而且我们已经把 \([l + 1, r - 1]\) 这个区间删掉了, 剩下的 \(a_l\) 和 \(a_r\) 一定能构成一个回文串 废话, 两个相等的树构成的串一定是回文的啊 (例如 11, 22, 33 ... 都是回文串)
于是, 我们就能够发现, 这样的区间的代价是 \([l + 1, r - 1]\) 的代价 +1
总结起来就是: 当 \(a_l == a_r\) 时,
然后我们考虑左右两个端点不相等的情况下该怎么做
很显然, 我们枚举一个 \(k\) , 把区间切成两部分 \([l, k]\) 和 \([k + 1, r]\) , 然后这样我们就能够从小区间转移到大区间了
248G
这也是区间DP板子
题意
每次可以合并相邻的两个数, 合并完以后的值是它们加一, 求能合并出的最大值
Solution
其实看这种合并一类的题目, 一般都是区间dp
于是我们考虑区间dp
设 \(dp[l][r]\) 表示 \(l\) 到 \(r\) 这个区间完全合并后能合并出的最大值
注意这里是完全合并以后, 原来的序列1 ~ n可能不能被完全合并, 因此答案并不是 \(dp[1][n]\) , 而是要枚举每个可能的 \(l\) 与 \(r\), 然后求最大值
对于一个区间 \([l, r]\) , 我们考虑枚举一个断点 \(k\) , 把区间分成 \([l, k]\) 和 \([k + 1, r]\)
然后我们发现如果这两个区间能够合并出的数相等, 我们显然可以让它们合并起来更新当前的 \(dp[l][r]\)
CF1178F1 Short Colorful Strip
题意
有一个长为 \(n\) 的纸带, 用 \(n\) 种颜色染它, 按照 \(1 ~ n\) 的顺序染色, 第 \(i\) 次染色的时候可以把这个纸带颜色相同的一个区间染成第i种颜色
给出一个最终的染色序列, 求染成最终的序列的方法有多少种
Solution
这题一看什么区间染色, 大概能猜到是区间dp
我们发现题中有一个重要的条件 按照1~n的顺序染色
由此可得, 染色的顺序是从小到大的
因此我们在考虑把一个区间 \([l, r]\) 染成最终染色序列的时候, 我们需要优先考虑最小的那个点, 要不然以后就没法再染成那种颜色了
所以, 对于每个区间 \([l, r]\) 我们考虑求出当前区间的最小值, 记最小值的位置是 \(pos\)
我们考虑把这个区间分成两部分, \([l, pos - 1]\) 和 \([pos + 1, r]\) , 记把两边染成最终染色序列的方案数分别为 \(lsum\) 和 \(rsum\)
显然, 根据乘法原理, 我们知道当前这个区间的方案数是 \(lsum * rsum\)
我们枚举 \(i\) 和 \(j\) ( $i \leq pos \leq j $ ) , 把区间 \([i, j]\) 刷成pos所对应的最小颜色
但是同时枚举 \(i\) 和 \(j\) 太费时间, 肯定会T
但是我们发现 \(i\) 和 \(j\) 的枚举其实没有直接关系, 对于 \(i\) 和 \(j\), 我们可以分别枚举, 然后让他们分别更新 \(lsum\) 和 \(rsum\) 即可
别忘了取模和开longlong
CF1198D Rectangle Painting 1
二维区间dp
题意
有n * n个方格, 每个方格中有 # 或 .
对于每个长方形, 定义它的价值是它长和宽的最大值
求覆盖所有
Solution
设 \(dp[x1][y1][x2][y2]\) 为覆盖 x1, y1, x2, y2 这个矩形中的 # 的最小价值
然后把一维区间dp枚举断点的思想搬到二维上, 分别枚举横断点和纵断点即可
树形DP
Zero Tree
设 \(f[u]\) 表示加的次数
设 \(g[u]\) 表示减的次数
然后就是树形dp的套路, 按照dfs的顺序更新即可
Day 9
状压dp
炮兵阵地
一看什么 \(m \leq 10\) 基本上就能确定这是一个状压dp
考虑把状态与起来, 判断冲突
这样然后枚举状态 (当前行, 上一行, 上上一行)
去掉冲突后更新答案
看似时间复杂度能到 \(O (10 ^ {11})\) 其实根本跑不满
常数超级小
数位DP
板子
int l, r;
int a[maxn];
int mem[maxn][10];
int len;
inline void get_num (int x) {
while (x) {
a[++len] = x % 10;
x /= 10;
}
}
int dfs (int now, int pre, bool limit, bool zero) {
if (now > len) { return 1; } // 搜完了 (既然搜过来了, 上一种搜索方式一定是合法的, 因此给答案加一)
if (not limit and mem[now][pre] != -1) { return mem[now][pre]; }
int res = 0;
int mx = limit ? a[len - now + 1] : 9;
for (int i = 0; i <= mx; i++) {
if ( abs(i - pre) < 2 ) { continue; } // 不符合题意 (差至少是2)
if (zero and i == 0) { res += dfs (now + 1, -2, limit and i == mx, true); } // 因为前导0, 所以下一位可以随便选, 要保证这一点, 首先就需要前一位是 -2, 这样无论怎么选都行
else { res += dfs (now + 1, i, limit and i == mx, false); }
}
if (not limit and not zero) { mem[now][pre] = res; }
return res;
}
inline int solve (int x) {
memset (mem, -1, sizeof (mem));
memset (a, 0, sizeof (a)); len = 0;
get_num (x);
return dfs (1, -2, true, true);
}
Day 10
DP 优化
决策单调性
斜率优化
啊啊啊啊啊啊啊
人生第一次学懂斜率优化
分治
奇怪的可撤销背包
Day 11
动态dp
Day 12 - ACM膜你赛
........
总之是寄了
非常有趣的是, 我们队叫"原神怎么你了", 然后我们后面一个队居然叫"不玩原神导致的"
我只会dp
然后只做出来一道数位dp和一车签到题 我太弱了
记录一下我们队开题顺序
-
C - A+-B (签到题)
题意是给定 \(a\) 和 \(b\) , 然后输出 \(a + b\) 或 \(a - b\)
我个人认为, 这题我这种
z班蒟蒻都能做这么简单的题还要做4min, 还抢不到一血 -
K - Intercepting Information (签到题2)
它...
甚至比C还简单
题意居然是给定8个数, 有9就输出
F, 否则输出S这...这也配K?!!
我这种
z班蒟蒻都轻松A掉那为什么比赛开始后10min过了 -
E - DRX vs. T1
它...
比K还简单
题意居然是给定一个字符串, 有3个T就输出
T1, 有3个D就输出DRX我这种
z班蒟蒻都一眼秒掉 -
B - Money Game
话说上面3个题真不适合当C班ACM模拟赛的题, 应该给我这种Z班蒟蒻做
所以B终于上难度了
我们发现, 允许 \(10 ^ {-6}\) 以内的误差, 并且, 数据趋近于无穷大
如果不存在一组稳定的解, 这题就基本不可做了
于是考虑构造一组稳定的解
什么? 构造? 我这种蒟蒻不会啊于是请出hyt大佬对于任意一组 \(a\), 我们考虑构造稳定, 可循环的解
我们先考虑给 \(a\) 中新加入一个 \(\bar a\), 然后令所有数都变为 \(\bar a\)
然后, 我们把新加入的 \(\bar a\) 附加在 \(a_1\) 上
再根据题意可知, \(\bar a\) 会在 \(a_1\) 到 \(a_n\) 和 \(a_n\) 到 \(a_1\) 中反复传播, \(a\) 中的值不会再变化
至此, 我们构造了出一组稳定的解
总结一下, 最终的 \(a\) 就是 \(\{2 * \bar a, \bar a, \bar a, \bar a, ... , \bar a \}\)
-
G - BOPC
嘿嘿上强度嘿嘿一看题, 这什么答辩?!!
然后我们考虑打表
打了个表, 通过
oeis差分, 找出规律然后
#define int __int128...然后居然在 1h 的时候 A 了
-
I - Lucky tickets
真正的强度上来了一眼看出是数位dp
但是怎么dp呢
我们想了很长时间
同时记录并维护mod + 二进制中1的个数 + 当前数对mod取余的结果真的是一件不可做并且很恶心人的事
所以我们考虑寻找更好的解决方案
我们想了很久, 发现, 题中要求mod必须等于二进制中1的个数, 于是我们考虑枚举1的个数, 这样模数直接就求出来了 (等于二进制中1的个数)
然后只需要维护当前数模上模数结果, 并且限制当前数二进制中1的个数不超过限制
于是这题就变得可做了
这题完全是我做的, 可能因为我们队其他大佬都不是很会dp吧然后自豪的贴上代码
#include <iostream> #include <algorithm> #include <string> #include <vector> #include <list> #include <stack> #include <map> #include <set> #include <cstdio> #include <cstring> #include <cmath> #include <queue> #define fastread ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); #define endl "\n" #define int __int128 using namespace std; inline void read(__int128 &x){ x=0; __int128 f=1; char ch=getchar(); while(!isdigit(ch)){ if(ch=='-')f=-1; ch=getchar(); } while(isdigit(ch)){ x=x*10+ch-'0'; ch=getchar(); } x*=f; } void write(__int128 x){ if(x<0){ putchar('-'); x=-x; } if(x<10)putchar(x%10+'0'); else{ write(x/10); putchar(x%10+'0'); } } const int maxn = 70; __int128 a; int stac[maxn]; int tot; int dp[maxn][maxn][maxn]; int mod; int dfs (int now, int cnt, int rem, bool lead, bool limit) { if(now>tot) { if (rem == 0 and cnt == mod) { return 1; } else { return 0; } } if (not limit and not lead and dp[now][cnt][rem] != -1) { return dp[now][cnt][rem]; } int mx = limit ? stac[tot - now + 1] : 1; int res = 0; for (int i = 0; i <= mx; ++i) { res += dfs (now + 1, cnt + i, (rem * 2 + i) % mod, lead and i == 0, limit and i == mx); } if (not limit and not lead) { dp[now][cnt][rem] = res; } return res; } int solve(){ while (a) { tot++; if (a & 1) { stac[tot]=1; } else { stac[tot]=0; } a >>= 1; } memset(dp,-1,sizeof(dp)); return dfs(1, 0, 0,true,true); } signed main () { // fastread read (a); int ans = 0; for (int i = 1; i <= 64; i++) { mod = i; ans += solve(); // cout << "i = " << i << " ans = " << ans << endl; } write(ans); return 0; }那个
define int __int128用来防RE就挺难绷的而且那个快读快写一看就不是我写的
韩岳佟的答辩码风而且这代码各种玄学操作常数上天 (比如
__int128), $ 2 \times 10 ^ 7 + \mathcal O(玄学)$ 居然能过我也是十分震惊的赛后我跟隔壁C39队的大佬sym交流, 他说 你..真不怕TLE啊 ...
此时我们队算是到了巅峰时期, rnk9, 这放在icpc我们都能Au了
但是接下来开题就有点困难了...
-
F - No Bug No Game
我们先开了一道看起来比较答辩的题
一看这么长的题面
果断机翻hyt和ky给我讲了好几遍题我才明白题意
然后我和hyt开始考虑dp, ky继续看别的题有没有可做的
然后hyt发现这似乎是一个类似背包的东西(确实), 然后他开始写
然后我看着他写, 越写越假
果然连样例都过不了
然后他开始调, hyt觉得样例太水
即使这样他也没过, 自己造了组数据然后调了114514年, 各种WA, 各种假, 罚时都吃上天了
最终, 我发现了一个惊奇的规律, 他的答案每次跟标准答案正好差2, 于是我们在输出之前补了一个
+ (rand() % 2) * 2然后过样例了...甚至还过了他出的数据然后交上去显然假了, 而且不只是假了, 还 WA on #2, 我真的... (显然, 他只过了样例#1)
然后我就觉得他想的不对, 一眼假啊, 我就重新读题然后准备做
然后我们又发现了一个规律, 每次只会有一个物品不会选最后一个物品(只有一个物品的重量不是 \(p[i]\) , 价值不是 \(w[i][p[i]]\) )
于是我们惊奇的发现, 枚举 \(i\) (那个不完全选的物品), 然后其他正常做背包不就行了
...
确实行
但是复杂度爆炸了怎么办, 即使 \(\text{vjudge}\) 的少爷机把我们上一题的 \(2e7 + \mathcal{O(玄学)}\) 给放过去了, 我真的不认为它能够容忍我们 \(9e9\) 外加升天常数
因此我们考虑优化
hyt大佬首先提出之前进行背包的dp数组可以再次使用
于是精通主席树的hyt大佬写了一个超级短的主席树, 然后发现好像空间会爆炸, 又不敢开了 (而且时间复杂度 \(9e6\) 外带1个log也不是很优)
然后hyt大佬不做了, 认为这题不可做, 去开J题了 (那是他最擅长的大模拟)
然后我和ky在旁边想F题思路
...
然后我就开始重新看题想题
想了114514年
我发现刚才我们的理解其实并没有什么大问题, 只是在可持久化的实现方式上有些问题
让我们重新考虑可持久化...
什么是可持久化? 为什么要用主席树这种毒瘤的东西?
我们发现主席树最大的用处在于面对区间问题是可以查询历史版本
然后我们考虑, 我们这个题中真正需要区间查询吗?
我想, 其实只需要查询出前缀和后缀就行, 有了前后缀, 枚举一个 \(x\) , 把 \(k\) 分成 \(x\) 和 \(k - x\) , 然后只查询两边dp即可
我们又发现, 对于一个背包, 它加入物品的顺序并不会影响它
于是我们考虑维护两个dp数组 \(dp1[i][j]\) 表示前 \(i\) 个物品重量限制为 \(j\) 的最大价值, \(dp2[i][j]\) 表示第 \(i\) 个物品到最后一个物品的重量限制为 \(j\) 的最大价值
然后对于每一个 \(i\) 我们就可以 \(O(1)\) 查询前缀和后缀的dp了
然后, 我犯了一个很严重的错误, 对于每个 \(i\) , 没有枚举它到底是那个取值 (就是 \(w[i][j]\) 中的 \(j\) 没有枚举), 而是直接取出了 \(w[i]\) 中的最大值
这是很严重的贪心, 一个好好的dp里面怎么能放贪心呢?!!
所以我思路假了
然后实现也必然假了
然后因为hyt用电脑调J题调了114514年, 导致只有20min给我写这题
我又非常紧张没有仔细考虑是否确实假了
于是到比赛结束也没有调出来...
难绷, 实际上, 我最后想出来的思路是我们队中最接近正解的
旁边C班39队的sym大佬想到了前两天学的缺一分治 (事实上我也想到了只是觉得多了个log, 我们队常数太大容易寄)
隔壁5队用的状压...这..., 明显没看出我们总结的那个性质...
总之是寄了
-
J - Tavern Chess
hyt大佬发现这是个大模拟, 然后花了114514年A掉了
间接导致了我F题没调出来(恼
总之是寄了
最终得分:

从rnk9掉到了rnk19sd
喜提Ag (然而只奖励前三名的大佬...)
这Ag是我们自己用来鼓励自己的, 根本不存在
Day 13
数论开始力
说句闲话, yzc老师昨晚没睡好, 导致他今天讲课的时候推出
我愿称他为yzc超级等式
再说句闲话, 下面这些板子, 请酌情在代码前加#define int __int128 或者 #define int long long 一类的东西
gcd
int gcd (int a, int b) {
if (not b) { return a; }
else { return gcd(b, a % b); }
}
这... 真...板子
lcm
同样给个板子吧
inline int lcm (int a, int b) { return a / gcd(a, b) * b; }
exGCD
我其实以前一直不是很懂 \(\mathcal exgcd\)
也许把板子背会了, 但是不是很明白
但是我觉得今天yzc讲的非常好
我们考虑我们在做gcd的时候是进行怎样的一个操作
我们实际上是每次把问题从 a, b 缩减到了 b, a % b
这就是欧几里得算法的思想
所以我们扩展欧几里得算法也应用的是这种思想
我们考虑对于每一个 a, b 如何把它转化为一个 b, a % b 的问题
然后我们发现直接把取模展开即可 (对m取模可以写成 \(k * m + b\) 中的 \(b\) )
然后中间详细过程不写了
贴个板子
int exgcd (int a, int b, int &x, int &y) {
if (not b) {
x = 1, y = 0;
return a;
}
int d = exgcd (b, a % b, y, x);
y -= a / b * x;
return d;
}
CRT && exCRT
中国剩余定理!!!
我爱中国剩余定理
但是很悲伤的一件事是我不会 \(\mathcal{exCRT}\)
但是师承zhx的我会大数翻倍法啊
bool merge (int &m1, int &a1, int m2, int a2) {
if (m1 < m2) { swap(m1, m2); swap(a1, a2); }
int tot = 0;
while (a1 % m2 != a2) {
if (++tot > m2 + 1) { return false; }
a1 += m1;
}
m1 = lcm (m1, m2);
return true;
}
// in main () :
// if (not merge (m, a, m_now, a_now)) { cout << "答辩" << endl; }
Lucas
现在是2023/07/30 0:43
累了, 睡觉, 明天再补, 总之Lucas模数不是质数时分解质因数然后在跟crt结合的思想太妙了 (例题似乎是古代猪文)
2023/08/07 20:06 好好好, 我现在才想起来补, 我真的太废物了
Day 14
关于埃氏筛和min_25/杜教筛出现在同一个课件中这件事
数论从入门到入土是吧
然后是莫比乌斯反演
总结起来, 看到什么 \([... = 1]\) , 直接开反!
Day 15
容斥 & 组合计数
Day 16
概率与期望 & 多项式 & 生成函数
概率与期望
概率, 就是一个事件发生的可能性的大小, 这非常显然
期望以前一直是一个我理解不了的概念
每次都是打开题, 看到期望, 关闭这个题
那么到底什么是期望?
其实跟生活中我们的期望是类似的
打完一场膜你赛, 我们常说, T1期望得分15pts, T2期望得分50pts ctl日常不会T1
那么我们考虑, 在这里面, 我们的
生成函数
???!!
Day 17
博弈论
博弈论其实就是博弈状态之间的转移
对于任意一个状态, 他为必胜态当且仅当所有可以变为当前状态都是必败态
(这是很显然的, )
NIM
Description
结论
所有数异或起来为零, 先手必败
怎么样理解呢?
我有一种感性理解, 我们考虑, 我们什么时候是必败的?
显然, 如果只有两堆, 它们数量是一样的, 那么这一定先手必败
因为我们先手取走任意一堆中的任意数量的石子, 后手可以用完全相同的策略在另一堆中取走相应的点, 使两堆数量再次相同, 从而又回到了开始时的局面
然后最后, 两堆石子归零, 一定是先手没有石子可以取了, 因此此时先手必胜
扩展
阶梯nim
先手必胜开局方案数
SG-function
Day 18
构造...
取模构造
例1
op差不多得了
像hyt和hzhl这样的火批也差不多得了
题意
对于一个 \(n\) 的排列 \(c\) , 构造两个 \(0 ~ n - 1\) 的 \(n\) 的排列 \(a\) 和 \(b\), 使得 \(c_i \equiv (a_i + b_i) \pmod n\)
若无法构造输出 \(-1\)
Solution
首先一眼构造
那么在构造之前, 先来判断是否有解
判断是否有解
输出-1其实能A好几个点
但是出题人捆绑subtask让你输出-1只能0分
那么考虑, 我们的 \(a\), \(b\) 和 \(c\) 都是 \(n\) 的排列, 所以无论它们是怎么样排的, 它们自己的和是不变的 (这是显然的)
所以根据等差数列求和公式, 我们有
那么我们不难推出
再由题意知 \(\sum a + \sum b\) 必须在模 \(n\) 意义下于 \(\sum c\) 同余
(因为每个 \(a_i + b_i\) 都在模 \(n\) 意义下与 \(c_i\) 同余 )
也就是说, 有解当且仅当 \(\sum a + \sum b \equiv \sum c \pmod n\)
那么有着我们可以推出什么呢
因为刚才的式子中左右两项都在模 \(n\) 意义下相等, 那么把它们相减就同余于 \(0\)
(就是移项)
形式化的
带入刚才的等差数列求和公式
移项可得
也即
等价于 \(\frac{n(n - 1)}{2}\) 被 \(n\) 整除 这也很显然
这式子看起来显然被 \(n\) 整除, 因为它分子里面有个 \(n\), 我们显然可以把他写成 \(n \times \frac{n - 1}{2}\)
但是, 有一种情况就是, 当后面乘的东西 \(\frac{n - 1}{2}\) 不是整数, 那么即便前面有个 \(n\) , 整个式子也不能被 \(n\) 整除, 也即这种情况下无解
由此可得, 无解当且仅当 \(\frac{n - 1}{2}\) 不是整数, 即 \(n - 1\) 是奇数, 也即 \(n\) 是偶数
所以
if (n % 2 == 0) { cout << -1 << endl; return 0; }
构造解
我们考虑, 如果令每个 \(a_i = b_i = \frac{c_i}{2}\) , 显然是满足 \(a_i + b_i = c_i\) 的
但是显然, 不一定每个 \(c_i\) 都是偶数, 也即不一定每个 \(a_i\) 和 \(b_i\) 是整数, 这显然不符合排列的定义
那么我们发现其实我们有一个重要的条件没有用上, 要求的是在模n意义下的相等
在模 \(n\) 意义下, 加个 \(n\) 不会影响什么
所以我们对于每个 \(c_i\) 是奇数的情况, 我们把他加上 \(n\) (有解的情况下 \(n\) 是奇数)
加上 \(n\) 以后, 显然它变成了偶数, 然后再对 \(n\) 取模, 就能构造出答案了
code : 略
为了水长度
代码来力
图上构造
Mister B and Flight to the Moon
Mister B and Flight to the Moon
经典图论构造
Day 19
膜你赛
保龄
唉
挂大分, 再挂分就要像ky一样上掉分榜了
逐题分析一下吧
T1
奇妙博弈论
似乎属于 \(nim\) 的扩展版
就是求先手必胜的开局方案数
T2
Day 20
字符串啊啊啊啊啊
不会串串啊...
字符串哈希
就是... 字符串的哈希...
额, 之前讲过, 所以代码咕咕咕
直接上例题
Sasha and One More Name
题目大意
给定回文串 \(s\), 把 \(s\) 切 \(k\) 刀分成 \(k + 1\) 部分, 对这些部分重新排列使它与 \(s\) 不相等且仍为回文串
求最小的 \(k\)
Solution
先来讨论是否有解
是否有解
观察样例可以得出, 如果我们的 \(s\) 里面的字符都是一样的, 显然无解, 输出 Impossible
如果 \(s\) 的长度使奇数, 那么除了中间一个点, 其他点一样同样是无解的 (无论怎么样都都不能够构建出来与 \(s\) 不同的回文串)
Solution
考虑一下有什么奇怪的性质
我们发现, 原来的 \(s\) 是回文串
我们发现, 在有解的情况下, 我们在回文中心的两边各切一刀, 然后两边交换, 必然可以构造出来符合要求的回文串
举个例子:
abacaba
那我们考虑从把它切成这样
ab | aca | ba
然后左右交换
ba | aca | ab
得到了满足要求的串串
为什么这是对的
显然
读者自证不难
但这其实确实挺显然的
实际上就是因为中间的一部分 aca 的中间回文的
然后两边原本就是对称的, 因此把 ab 和 ba 交换同样不影响回文这一性质
显然, 这样交换与 \(s\) 是不同的, 因此满足要求
至此, 我们可以知道, 答案只能是 \(1\) 或者 \(2\)
那么考虑有没有可能是 \(1\) 当然可以, 要不然这题哪用了字符串哈希啊
因为答案是 \(1\), 我们直接枚举断点, 然后把两边交换一下, 判断是否满足条件即可
冷知识
这题 \(s\) 长度是 \(5e3\) 级别的
所以...
写啥哈希啊, string.substr() 他不香吗
所以我没写字符串哈希 以此掩盖我不会的事实
但其实写哈希要推式子, hyt调一下午, 我20min写完并AC, 时常只比他慢15ms
问题不大
奉上超短代码
cin >> s; int n = s.size();
// 判断无解
int cnt = 0;
for (int i = 0; i < (n >> 1); i++) {
cnt += s[i] != s[0];
}
if (not cnt) { cout << "Impossible" << endl; return 0; }
// 枚举断点
for (int i = 1; i <= (n >> 1); i++) {
string T = s.substr(i, n) + s.substr(0, i);
string S = T; reverse(S.begin(), S.end());
if (S == T and T != s) { // 满足要求
cout << 1 << endl;
return 0;
}
}
cout << 2 << endl; // 其他情况答案就是2
Trie
本身不难
所以..
代码咕咕咕
Xor-MST
图上奇怪的最小生成树
kmp
核心是 \(next\) 数组
考虑有文本串 \(s\), 和模式串 \(t\)
然后, 进行匹配
先考虑暴力匹配, 用两个下标 \(i\) 和 \(j\) 分别遍历 \(s\) 和 \(t\)
复杂度显然升天, 是 \(O(hytの密码大质数)\) 吗 显然不是这样的
喷一下hyt为了防止我jc他把他电脑密码设成45位大质数了
然后我们发现, 暴力匹配的过程中, 如果匹配失败了, \(j\) 必须回到起点
那么, 这就造成了我们的复杂度飙升到了 \(\mathcal{O(n * m)}\) 确实升天
我们发现, 每次退回起点真的好烦啊
那假如我们不想退回起点怎么办呢?
欸, 所以我们直接看一看 \(t\) 中与 以当前下标 \(j\) 为结尾的后缀 相等的的最长前缀是什么
然后把当前后缀回退到那个最长前缀不就行了 (这其实就是利用了我们之前已经匹配过了的模式串1~j是与文本串是相等的)
AC自动机
多模匹配
其实就是用 \(trie\) 存一下模式串
为什么AC自动机比做 \(n\) 遍 \(kmp\) 快
就是因为AC自动寄是对所有模式串同时进行匹配, 这样就能非常快
也就是说, 我们之前, \(kmp\) 每个模式串的 \(next\) 实际上是对自己的一个匹配
我们现在在模式串构成的 \(trie\) 上进行一个模式串之间的匹配, 在树上添加一些 \(fail\) 指针, 使 \(trie\) 变成一个 \(DAG\) , 然后在 \(DAG\) 上进行匹配
就能实现我们刚才说的 同时进行匹配
代码暂时咕咕咕
Day 21
exkmp
就是扩展kmp...
会啦, 感谢MichaelWong
应用
本质不同子串数
回文自动机
会啦, 感谢hzhl
红着眼, 含着泪,活着回来 这就是hzhl吗 (
Day 22
后缀数组
后缀自动机
后缀自动寄
不会, 咕咕咕
Day 23
又是膜你赛
寄了 (悲)
T3 挂100pts, 至今未破案
T1 比较幸运, 喜提100pts
但是T1真的好水啊...
考场上花了 1h ...
原因竟然是我一直在想 \(n \leq 7000\) 的时候 \(\mathcal{O(n ^ 2)}\) 能不能跑过去
然后...
赛后发现 MichaelWong \(\mathcal{O(n ^ 2 \log n)}\) 都*过去了...
我: ??!!!
好好好, 我承认我不相信现代计算机的速度, 我的思想还停留在 \(\mathcal{O(n ^ 2)}\) 的复杂度 \(n \leq 1000\) 都很难跑过去...
我这么年轻的选手居然落后了呜呜呜
当然, 有些黑科技还是可以用的
比如说 nth_element 复杂度是 \(O(n)\)
用法大概就是:
// 假设a长度为n, 下标从1开始
inline int get_k (const int a[], int k) {
nth_element(a + 1, a + k, a + n + 1);
return a[k];
}
STL大法好
小周老师说必须用stl
然后, 然后开始肝T3
然后...
保龄
Day 24
ACM
我正好贡献一坤题 两题半 的完整思路和代码
剩下的是我, hyt, ky合作的...
我还是太弱了
主要我不是主代码手...
Day 25
图论...
DFS
学之前: ???!! C班还讲这东西?
学之后: 好好好
DFS环套环
我们对图构造一棵 \(dfs\) 树, \(dfs\) 树上任意一条非树边对应着一个环
图上任意一个环都可以由一些简单环异或出来
(简单环指的是不经过重复的点)
然后上例题罢
P4151 [WC2011] 最大XOR和路径
WinterCamp 2011 ??
P4151 [WC2011] 最大XOR和路径 (se
Description
给定 \(n\) 个点, \(m\) 条边的一个无向图, 每个点有一个权值
求 \(1\) 到 \(n\) 的一条异或值最大的路径
Solution
首先, 我们的图上显然存在一条 \(1\) 到 \(n\) 最优的道路 (这就是答案啊)
然后, 我们考虑再随意构造一条从 \(1\) 到 \(n\) 的道路
那现在我们就有了两条路径
我们发现这两条路径, 构成了一个环!
然后再由上面的结论我们可以知道, 这个环它可以由几个简单环异或出来
所以我们知道这条最优的道路等于随意找的一条路径再异或上一些简单环, 并使它们异或值最大
然后大佬说: 一个线性基秒了
我:
欸, 等等, 我不会线性基啊
...
那么来学习一下线性基
线性基
线性只因
咕咕咕
上个板子 其实不难
namespace Basis {
typedef unsigned long long ll;
ll a[64];
inline void insert (ll x) {
for (int i = 63; i >= 0; i--) {
if (not (x & (1ll << i))) { continue; }
if (a[i]) { x ^= a[i]; }
else { a[i] = x; return; }
}
}
inline ll query (ll x = 0) {
for (int i = 63; i >= 0; i--) {
if ((x ^ a[i]) > x) { x ^= a[i]; }
}
return x;
}
}
拓扑排序
就是... 拓扑排序
果然 ZJ noip 和 SD noip 都不是一个水平的
正睿普及严格大于ioi
QBXT 老师还讲了很长时间板子
dcx发现大家都会了, 直接开始讲题
板子
还是贴一份吧
vector <int> res;
void topsort ()
{
queue<int> q;
for (int i = 1; i <= n; i++)
{
if (ind[i] == 0) q.push (i);
}
while (not q.empty())
{
int now = q.front();
res.push_back (t);
for (int i = last[now]; i; i = pre[i])
{
int t = to[i];
ind[t] --;
if (ind[t] == 0)
{
q.push (t);
}
}
}
}
Problems
DAG上最长链
Descrpition
就是求DAG上的最长链
没有数据
复杂度要求线性
Solution
...
这题我会
拓扑排序然后dp吗
比较显然
dcx: 到现在一眼看不出这题可以考虑退役~
好好好
Tarjan
强连通分量
目前我见过最优雅的写法
int low[maxn], dfn[maxn], dpos;
stack<int> stk;
bool ins[maxn];
int scc[maxn], scc_cnt;
void tarjan (int now)
{
low[now] = dfn[now] = ++dpos;
stk.push(now);
ins[now] = true;
for (int i = last[now]; i; i = pre[i])
{
int t = to[i];
if (not dfn[t])
{
tarjan (t);
low[now] = min (low[now], low[t]);
}
else if (ins[t])
{
low[now] = min (low[now], dfn[t]);
}
}
if (low[now] == dfn[now])
{
scc_cnt++;
do{
scc[now] = scc_cnt;
now = stk.top(); stk.pop(); ins[now] = false;
} while (low[now] != dfn[now]);
}
}
Day 25
欧拉回路
判定条件
有向图: 入度等于出度
无向图: 度数是偶数
感性理解吧
就是对于每个点我们都能进去能出来, 所以必然存在...
找欧拉回路
Hierholzer
wkl@qbxt 讲过
当前弧优化
for (int &i = last[now]; i; i = per[i]) // &引用
例题
Mike and Fish
Decription
平面上有n个点, 每个点可以染成蓝色或者红色
同一行蓝色与红色
Solution
2-SAT
qbxt里也讲过
大概就是tarjan缩点然后dag上乱搞进行一些操作
例题
NOI2017 游戏
\(d \leq 8\) 发现可以暴力枚举
这里有一个暴力枚举的小技巧, 枚举 AC, AB 两种情况, 就能够包含 A, B, C 这三种车
然后变成2-SAT板子题了
[北京省选集训2019] 完美塔防
2-SAT 奇妙建模题
这题甚至需要物理只是 虽然只需要知道光路可逆就行了
同余最短路
就是按同余类进行划分以后连边
然后考虑转移连边
我们用最短路跑出每个同余类中能被表示出来最小的数
然后就能够算出同余类中可以被表示出来的数的个数
加起来就是答案
Day 26
网络流
嘿嘿流流嘿嘿
Dinic
至今仍然记得, 在qbxt, 调dinic板子调了6h, 发现返回值是bool...
所以再写一遍dinic吧
namespace Net {
struct Edge {
int u, v, pre;
int flow;
};
Edge es[maxn];
int last[maxn], cur[maxn], cnt = 1; // cnt从1开始容易求出反向边
bool vis[maxn];
inline void _addEdge (int u, int v, int cap) {
cnt ++;
es[cnt].u = u;
es[cnt].v = v;
es[cnt].flow = cap;
es[cnt].pre = last[u];
last[u] = cnt;
}
inline void addEdge (int u, int v, int cap) {
_addEdge(u, v, cap);
_addEdge(v, u, cap);
}
inline void init () {
cnt = 1;
memset (last, 0, sizeof(last));
memset (vis, 0, sizeof(vis));
}
int S, T;
int dep[maxn]; // 分层
inline bool bfs () {
memset (dep, 0x3f, sizeof(dep));
dep[S] = 0;
queue<int> q; q.push(S);
while (not q.empty()) {
int now = q.front(); q.pop();
for (int i = last[now]; i; i = es[i].pre) {
int t = es[i].v;
if (dep[t] == 0x3f3f3f3f and es[i].flow != 0) { // 没被访问过且有流量
dep[t] = dep[now] + 1;
q.push(t);
}
}
}
return dep[T] != 0x3f3f3f3f;
}
inline int dfs (int now, int now_flow) {
if (now_flow == 0 or now == T) { return now_flow; } // 没有流量了或者到了
int res = 0;
for (int &i = cur[now]; i; i = es[i].pre) {
int t = es[i].v;
if (es[i].flow == 0 or dep[t] != dep[now] + 1) { continue; } // 没流量了 或者 不是下一层
int t_flow = dfs(t, min(now_flow, es[i].flow)); // 不能超过流量限制
if (t_flow) { // 能流到t
es[i].flow -= t_flow; // 这条边的容量被消耗了
es[i ^ 1].flow += t_flow; // 反悔边
res += t_flow;
now_flow -= t_flow;
if (not now_flow) { return res; } // 当前的流量被耗尽了
}
}
return res;
}
int dinic (int _s, int _t) {
S = _s, T = _t;
int res = 0;
while (bfs ()) {
memcpy (cur, last, sizeof(last)); // 把
res += dfs (S, 0x3f3f3f3f); // 源点有无限的流量
}
return res;
}
void find_min_cut (int now) {
vis[now] = true;
for (int i = last[now]; i; i = es[i].pre) {
int t = es[i].v;
if (vis[t]) { continue; } // 不重复访问
if (es[i].flow <= 0) { continue; } // 有流量的才能流
find_min_cut(t);
}
}
inline void output_min_cut (vector<pair<int, int> > edges) {
for (auto x : edges) {
int u = x.first;
int v = x.second;
if (vis[u] ^ vis[v]) { cout << u << " " << v << endl; }
}
cout << endl;
}
}
最大流 = 最小割
关于最小割输出方案
直接在图上再跑一边dfs
沿着没满流的边搜索
每条边的两个端点颗一个能搜到一个不能搜到, 这条边就被割掉了
然后...
网络流建模来力!!
建模
圆桌问题
最长不下降子序列问题
切糕
一刀下去一个clb
咕咕咕
Day 27
啊啊啊费用流啊啊啊啊
完了现在一看到网络流就想发电
网络流24题
T3 飞行员配对方案问题
T5 太空飞行计划问题
Day 28
dfs树
无向图dfs树所有非树边都是返祖边
感性理解
无向图本身联通, 假设现在有一个点 \(x\), 他子树中有两个个点分别是 \(u\), \(v\) 且 \(u\) 和 \(v\) 中有一条边
我们在遍历到 \(u\) 的时候一定会遍历到 \(v\) (因为他们之间有一条边)
所以从 \(v\) 回到 \(x\) 的那条边成为了非树边, 那么这时候这条边一定是返祖边
Ehab's Last Corollary
奇妙构造
如果是树, 黑白染色后取最大独立集
如果不是树, 取最小环, 看是长度否小于等于 \(k\)
-
小于等于 \(k\) 则直接输出环
-
大于 \(k\) 就在环上黑白染色, 求出独立集
关于求无向图的环长
因为dfs树上所有非树边都是返祖边
所以当我们找到一条返祖边, 这个环的长度显然是这条边两端点的深度之差加一
形式化的, 对于一条两端点为 \(u\) 和 \(v\) 的(非树)返祖边, 我们存在一个环长为 $ \lvert dep_u - dep_v \rvert + 1 $
随机化
\(i_1, i_2, \cdots , i_a\)
\(\max_{j=1}^a i_j - \min_{j=1}^a i_j + 1 > a\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号