【解题收藏】【宫水三叶の相信科学系列】详解何为拓扑排序,以及求拓扑排序方法的正确性证明
基本分析 & 拓扑排序
为了方便,我们令点数为 $n$,边数为 $m$。
在图论中,一个有向无环图必然存在至少一个拓扑序与之对应,反之亦然。
如果对拓扑排序不熟悉的小伙伴,可以看看 拓扑排序。
简单来说,就是将图中的所有节点展开成一维序列,对于序列中任意的节点 $(u, v)$,如果在序列中 $u$ 在 $v$ 的前面,则说明在图中存在从 $u$ 出发达到 $v$ 的通路,即 $u$ 排在 $v$ 的前面。反之亦然。
同时,我们需要知晓「入度」和「出度」的概念:
- 入度:有多少条边直接指向该节点;
- 出度:由该节点指出边的有多少条。
因此,对于有向图的拓扑排序,我们可以使用如下思路输出拓扑序(BFS 方式):
- 起始时,将所有入度为 $0$ 的节点进行入队(入度为 $0$,说明没有边指向这些节点,将它们放到拓扑排序的首部,不会违反拓扑序定义);
- 从队列中进行节点出队操作,出队序列就是对应我们输出的拓扑序。
对于当前弹出的节点 $x$,遍历 $x$ 的所有出度,即遍历所有由 $x$ 直接指向的节点 $y$,对 $y$ 做入度减一操作(因为 $x$ 节点已经从队列中弹出,被添加到拓扑序中,等价于从 $x$ 节点从有向图中被移除,相应的由 $x$ 发出的边也应当被删除,带来的影响是与 $x$ 相连的节点 $y$ 的入度减一); - 对 $y$ 进行入度减一之后,检查 $y$ 的入度是否为 $0$,如果为 $0$ 则将 $y$ 入队(当 $y$ 的入度为 $0$,说明有向图中在 $y$ 前面的所有的节点均被添加到拓扑序中,此时 $y$ 可以作为拓扑序的某个片段的首部被添加,而不是违反拓扑序的定义);
- 循环流程 $2$、$3$ 直到队列为空。
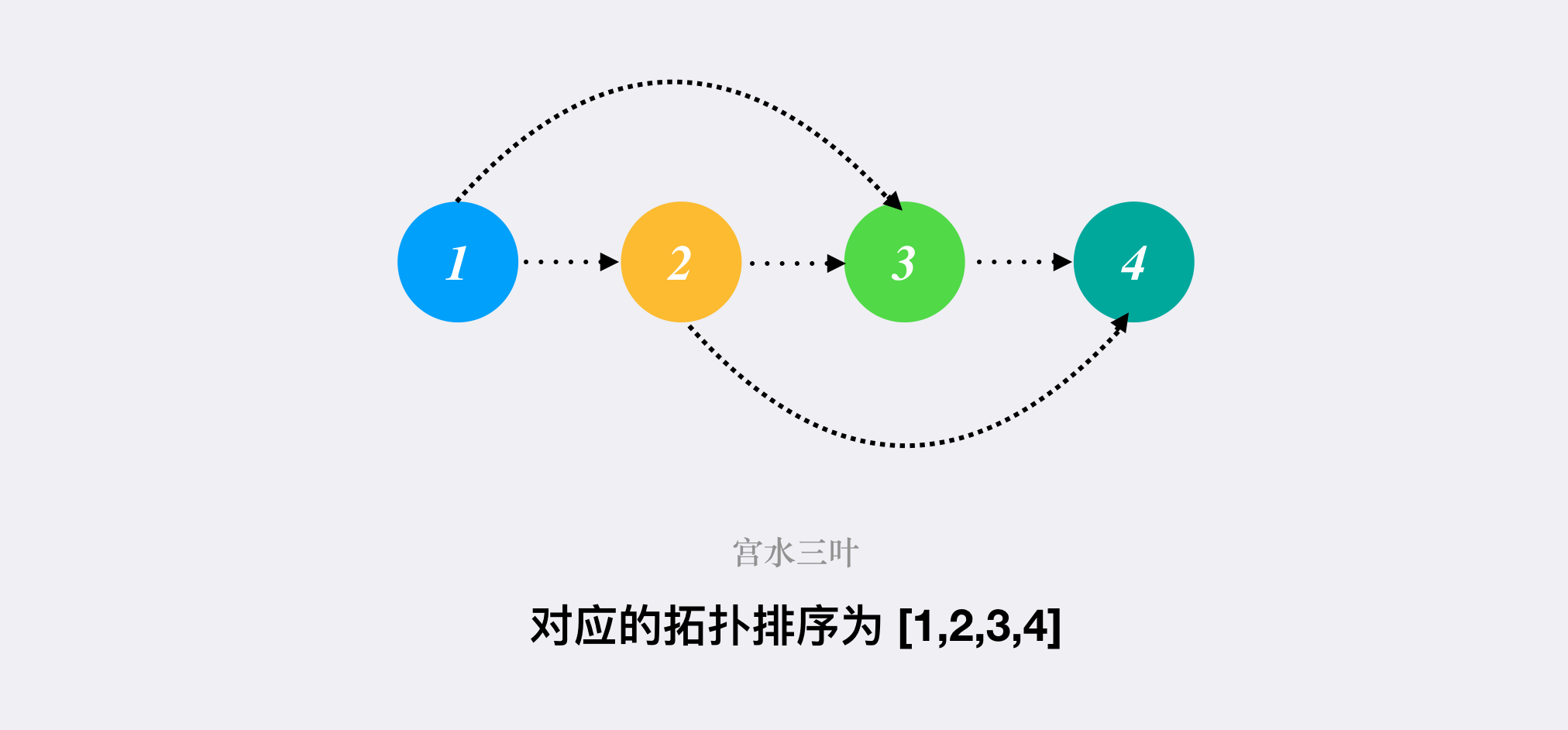
证明
上述 BFS 方法能够求得「某个有向无环图的拓扑序」的前提是:我们必然能够找到(至少)一个「入度为 $0$ 的点」,在起始时将其入队。
这可以使用反证法进行证明:假设有向无环图的拓扑序不存在入度为 $0$ 的点。
那么从图中的任意节点 $x$ 进行出发,沿着边进行反向检索,由于不存在入度为 $0$ 的节点,因此每个点都能够找到上一个节点。
当我们找到一条长度为 $n + 1$ 的反向路径时,由于我们图中只有 $n$ 个节点,因此必然有至少一个节点在该路径中重复出现,即该反向路径中存在环,与我们「有向无环图」的起始条件冲突。
得证「有向无环图的拓扑序」必然存在(至少)一个「入度为 $0$ 的点」。
即按照上述的 BFS 方法,我们能够按照流程迭代下去,直到将有向无环图的所有节点从队列中弹出。
反之,如果一个图不是「有向无环图」的话,我们是无法将所有节点入队的,因此能够通过入队节点数量是否为 $n$ 来判断是否为有向无环图。
反向图 + 拓扑排序
回到本题,根据题目对「安全节点」的定义,我们知道如果一个节点无法进入「环」的话则是安全的,否则是不安全的。
另外我们发现,如果想要判断某个节点数 $x$ 是否安全,起始时将 $x$ 进行入队,并跑一遍拓扑排序是不足够的。
因为我们无法事先确保 $x$ 满足入度为 $0$ 的要求,所以当我们处理到与 $x$ 相连的节点 $y$ 时,可能会存在 $y$ 节点入度无法减到 $0$ 的情况,即我们无法输出真实拓扑序中,从 $x$ 节点开始到结尾的完整部分。
但是根据我们「证明」部分的启发,我们可以将所有边进行反向,这时候「入度」和「出度」翻转了。
对于那些反向图中「入度」为 $0$ 的点集 $x$,其实就是原图中「出度」为 $0$ 的节点,它们「出度」为 $0$,根本没指向任何节点,必然无法进入环,是安全的;同时由它们在反向图中指向的节点(在原图中只指向它们的节点),必然也是无法进入环的,对应到反向图中,就是那些减去 $x$ 对应的入度之后,入度为 $0$ 的节点。
因此整个过程就是将图进行反向,再跑一遍拓扑排序,如果某个节点出现在拓扑序列,说明其进入过队列,说明其入度为 $0$,其是安全的,其余节点则是在环内非安全节点。
另外,这里的存图方式还是使用前几天一直使用的「链式前向星」,关于几个数组的定义以及其他的存图方式,如果还是有不熟悉的小伙伴可以在 这里 查阅,本次不再赘述。
代码:
class Solution {
int N = (int)1e4+10, M = 4 * N;
int idx;
int[] he = new int[N], e = new int[M], ne = new int[M];
int[] cnts = new int[N];
void add(int a, int b) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
public List<integer> eventualSafeNodes(int[][] g) {
int n = g.length;
// 存反向图,并统计入度
Arrays.fill(he, -1);
for (int i = 0; i < n; i++) {
for (int j : g[i]) {
add(j, i);
cnts[i]++;
}
}
// BFS 求反向图拓扑排序
Deque<integer> d = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
if (cnts[i] == 0) d.addLast(i);
}
while (!d.isEmpty()) {
int poll = d.pollFirst();
for (int i = he[poll]; i != -1; i = ne[i]) {
int j = e[i];
if (--cnts[j] == 0) d.addLast(j);
}
}
// 遍历答案:如果某个节点出现在拓扑序列,说明其进入过队列,说明其入度为 0
List<integer> ans = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (cnts[i] == 0) ans.add(i);
}
return ans;
}
}
- 时间复杂度:$O(n + m)$
- 空间复杂度:$O(n + m)$
最后
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
也欢迎你 关注我 ,提供写「证明」&「思路」的高质量专项题解。
所有题解已经加入 刷题指南,欢迎 star 哦 ~
本题解共分为 $4$ 个部分,大家可根据自身情况选择性阅读:
- 题目解析(针对题目叙述可能难以理解的点进行详解,可以跳过)
- 为什么要用拓扑排序,以及什么是拓扑排序?
- 拓扑排序的图示(帮助大家理解拓扑排序,如已掌握可跳过)
- 代码(C++/Java版)
1. 题目解析
发现很多朋友们都吐槽题目的翻译问题,那么在这里我们先结合样例帮大家梳理一下:😃
题目中关键的一句:对于一个起始节点,如果从该节点出发,无论每一步选择沿哪条有向边行走,最后必然在有限步内到达终点,则将该起始节点称作是安全的。
也就是说,对于某一个节点,如果它当前在某个环内,或者有可能走到某个环上,那么它就是不安全的,因为如果遇到环,就无法在有限步内到达终点。
我们结合样例一来看:
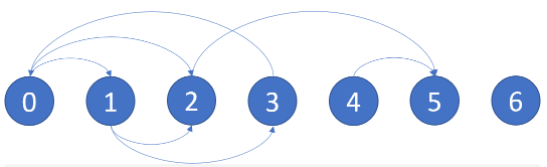
输入:graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出:[2,4,5,6]
其中输入的graph数组中的元素代表了各点的指向情况,例如第一个元素[1,2]就表示以节点0为起点的边有两条,分别指向节点1和节点2。
输出为[2,4,5,6],首先图中节点5和6都是出度为 $0$ 的节点,他们本身就是终点,而2和4的情况相同,他们的出度都为 $1$,且都指向节点5,所以他们只能通过这条边走向终点5。
2. 为什么要用拓扑排序,以及什么是拓扑排序?
- 根据上面的分析,我们发现,最简单的安全点就是无路可走的终点(也即出度为 $0$ 的节点)。而拓展到一般情况,如果一个节点所指向的点均为安全点,那么这个点也是安全点。如何提取出这些安全点呢?我们需要避开图中的环路,提到环路,我们会自然地想到拓扑排序,我们试试拓扑排序能否完成这道题。
拓扑排序:从给定的图的所有边中「提取出该图的某一个拓扑序列」的过程,拓扑序列是一条满足图中有向边前后关系的序列,任一有向边起点在序列中一定早于终点出现。如果图中有环,则无法提取出拓扑序列。所以拓扑排序的一个重要应用是在给定的有向图中判定是否存在环路。
- 拓扑排序是找到图中入度为 $0$ 的节点,以及仅由入度为 $0$ 节点所指向的节点。 ,而本题是找到图中出度为 $0$ 的节点,以及仅指向出度为 $0$ 节点的节点。刚好是相反的情况,所以,我们将题目给定的有向图变为反图(也即有向边的起点、终点互换),那么所有安全点便可以通过拓扑排序来求解了。
- 接下来,我们简述一下拓扑排序的思想,并证明一下我们算法的有效性:
(1)将所有入度为 $0$ 的点(原图中出度为 $0$ 的点,也就是终点,最简单的安全点)加入队列。
(2)每次循环访问位于队头的节点(安全点);
(3)遍历以该节点为起点的所有有向边,将其从图中去掉,也即将将该点指向的所有点的入度减一。
(4)若某被指向点入度变为 $0$(意味着指向这个点的点均曾经被加入过队列,说明均为安全点),则将此点入队
(5)重复步骤(2)、(3)、(4)直至队空。
### 3. 拓扑排序的图示(帮助大家理解拓扑排序,如已掌握可跳过) > Tips:下面的图示和说明可以帮大家更好的理解拓扑排序的过程
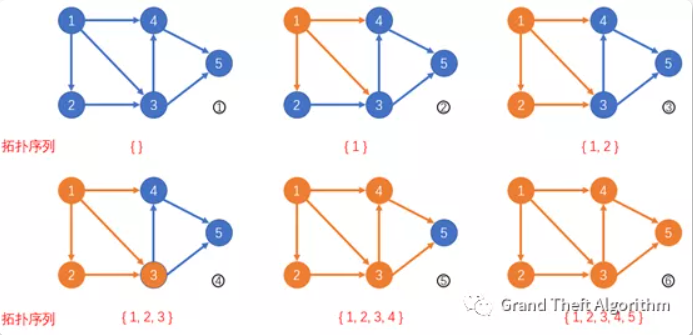
首先,给定图中仅有节点 $1$ 入度为 $0$,我们将其加入队列。
我们将节点 $1$ 为起点的有向边均删掉(在图中变为橙色),更新这些有向边终点的入度,节点 $2,3,4$ 入度均减一,变为 $[0,1,1]$。由于节点 $2$ 的入度变为了 $0$,我们将其加入队列。
我们将节点 $2$ 为起点的有向边均删掉,更新这些有向边终点的入度,节点 $3$ 入度减一,变为 $[0]$。我们将其加入队列。
我们将节点 $3$ 为起点的有向边均删掉,更新这些有向边终点的入度,节点 $4,5$ 入度均减一,变为 $[0,1]$。由于节点 $4$ 的入度变为了 $0$,我们将其加入队列。
我们将节点 $4$ 为起点的有向边均删掉,更新这些有向边终点的入度,节点 $5$ 入度减一,变为 $[0]$。由于节点 $5$ 的入度变为了 $0$,我们将其加入队列。
我们将节点 $5$ 为起点的有向边均删掉,此时全图已经遍历完毕,没有新的节点被加入队列。
队列为空,拓扑排序结束。
如果你仍然想更多地了解拓扑排序,可以阅读我们写的拓扑排序专题。在这之后,你可能会想拿下面几道题练练手:
LeetCode 207.课程表 (中等)
LeetCode 210.课程表II (中等)
LeetCode 329.矩阵中的最长递增路径 (困难)
LeetCode 1203.项目管理 (困难)
4. 代码(C++/Java版)
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
int n = graph.size();
// 反图,邻接表存储
vector<vector<int>> new_graph(n);
// 节点入度
vector<int> Indeg(n, 0);
for(int i = 0; i < n; i++) {
for(int x : graph[i]) {
new_graph[x].push_back(i);
}
// 原数组记录的节点出度,在反图中就是入度
Indeg[i] = graph[i].size();
}
// 拓扑排序
queue<int> q;
// 首先将入度为 0 的点存入队列
for(int i = 0; i < n; i++) {
if(!Indeg[i]) {
q.push(i);
}
}
while(!q.empty()) {
// 每次弹出队头元素
int cur = q.front();
q.pop();
for(int x : new_graph[cur]) {
// 将以其为起点的有向边删除,更新终点入度
Indeg[x]--;
if(!Indeg[x]) q.push(x);
}
}
// 最终入度(原图中出度)为 0 的所有点均为安全点
vector<int> ret;
for(int i = 0; i < n; i++) {
if(!Indeg[i]) ret.push_back(i);
}
sort(ret.begin(), ret.end());
return ret;
}
};
class Solution {
public List<integer> eventualSafeNodes(int[][] graph) {
int n = graph.length;
// 反图,邻接表存储
List<list<integer>> new_graph = new ArrayList<list<integer>>();
// 节点入度
int[] Indeg = new int[n];
for(int i = 0; i < n; i++) {
new_graph.add(new ArrayList<integer>());
}
for(int i = 0; i < n; i++) {
for(int j = 0; j < graph[i].length; j++) {
new_graph.get(graph[i][j]).add(i);
}
// 原数组记录的节点出度,在反图中就是入度
Indeg[i] = graph[i].length;
}
// 拓扑排序
Queue<integer> q = new LinkedList<integer>();
// 首先将入度为 0 的点存入队列
for(int i = 0; i < n; i++) {
if(Indeg[i] == 0) {
q.offer(i);
}
}
while(!q.isEmpty()) {
// 每次弹出队头元素
int cur = q.poll();
for(int x : new_graph.get(cur)) {
// 将以其为起点的有向边删除,更新终点入度
Indeg[x]--;
if(Indeg[x] == 0) q.offer(x);
}
}
// 最终入度(原图中出度)为 0 的所有点均为安全点
List<integer> ret = new ArrayList<integer>();
for(int i = 0; i < n; i++) {
if(Indeg[i] == 0) ret.add(i);
}
return ret;
}
}
- 时间复杂度:$O(n+m)$,$n$为节点个数,$m$为边的条数。
- 空间复杂度:$O(n+m)$,用于存图。
结语
我们是GTA小分队,一群就读于北航、人大、中科院、北理等学校的计算机专业本科生和研究生。我们的公众号 【GTAlgorithm】 专注于算法专题、比赛题解、大厂面经的分享,目前已有 $170+$ 篇原创作品,致力于陪大家一起收割大厂offer。
欢迎大家【点赞】 和 【分享】 ,也欢迎在评论区与我们交流,点击我关注公众号后回复【进群】可加入刷题群,回复 【面经】 可获得真实大厂面经(附带答案)~~</list



 浙公网安备 33010602011771号
浙公网安备 33010602011771号