代码随想录算法训练营|Day 24

Day 24

第七章 回溯算法part03

93.复原IP地址

本期本来是很有难度的，不过 大家做完 分割回文串 之后，本题就容易很多了

题目链接/文章讲解：https://programmercarl.com/0093.复原IP地址.html
视频讲解：https://www.bilibili.com/video/BV1XP4y1U73i/

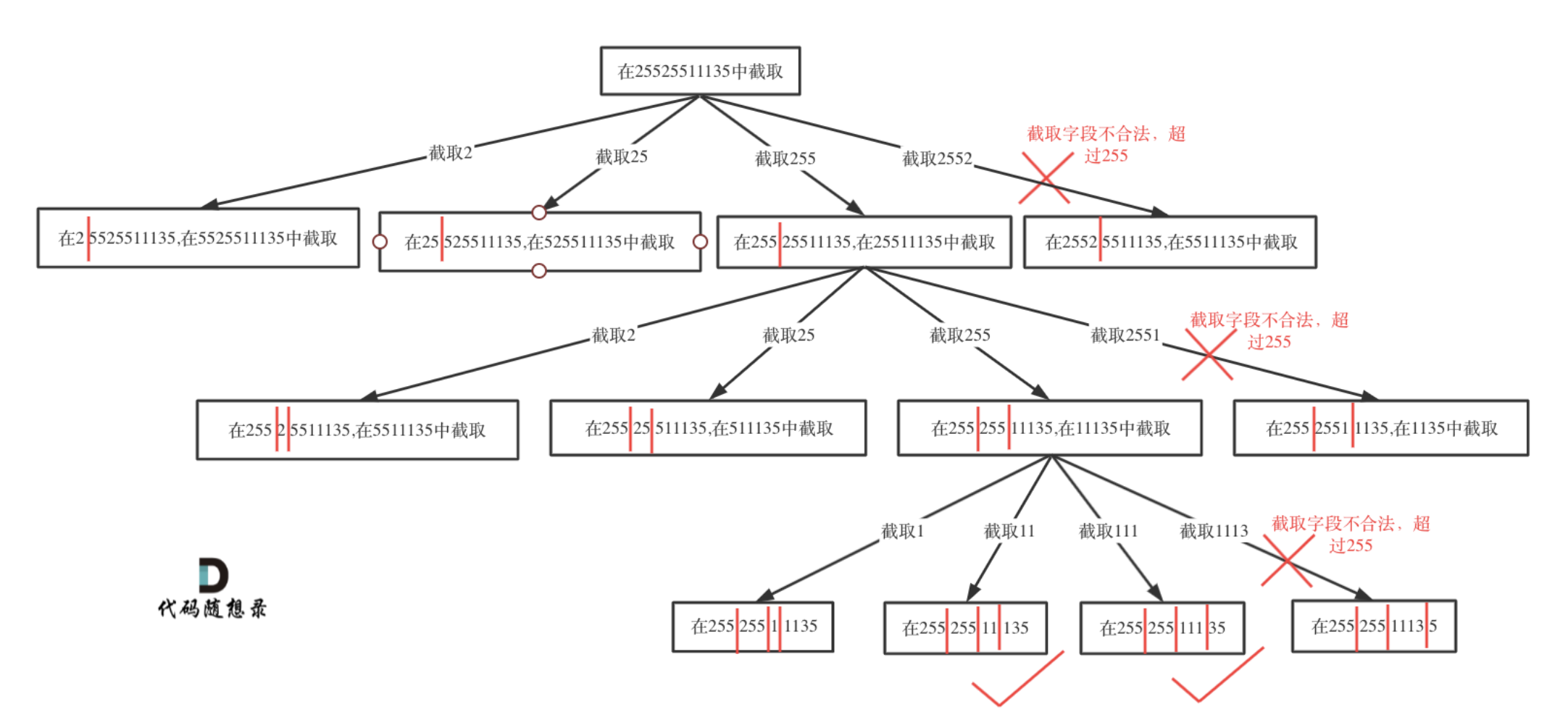
回溯三部曲

• 递归参数

  需要startIndex,因为不能重复分割，要记录下一层递归分割的起始位置

• 递归终止条件

  与分割回文串的差异：

  分割回文串的终止条件是切割线切到最后

  本题则要求切割段数，只会分为4段

• 单层搜索的逻辑

  在for (int i = startIndex; i < s.size(); i++)循环中 [startIndex, i] 这个区间就是截取的子串，需要判断这个子串是否合法。

  判断子串是否合法：

  • 段位以0为开头的数字不合法

  • 段位如果大于255了不合法

class Solution:
    def backtracking(self, string, index, path, result):
        if index >= len(string) and len(path) == 4:
            result.append('.'.join(path))
            return
        if len(path) > 4:
            return
        for i in range(index, min(index+3,len(string))):
            substring = string[index:i+1]
            ##判断是否有效
            if len(substring) > 1 and substring[0] == "0":
                break
            if int(substring) > 255:
                break           
            self.backtracking(string, i+1, path+[substring],result)
                    
    def restoreIpAddresses(self, s: str) -> List[str]:
        result = []
        self.backtracking(s, 0, [], result)
        return result

78.子集

子集问题，就是收集树形结构中，每一个节点的结果。 整体代码其实和 回溯模板都是差不多的。

题目链接/文章讲解：https://programmercarl.com/0078.子集.html
视频讲解：https://www.bilibili.com/video/BV1U84y1q7Ci

子集问题 vs 组合/分割问题：

组合/分割问题是收集树的叶子节点，而子集问题是找树的所有节点

---

“子集问题中，依靠index去控制切分位置无法得到我们想要的path中的元素顺序

例如：[1,2,3] 子集中要得到[1,3]”

---

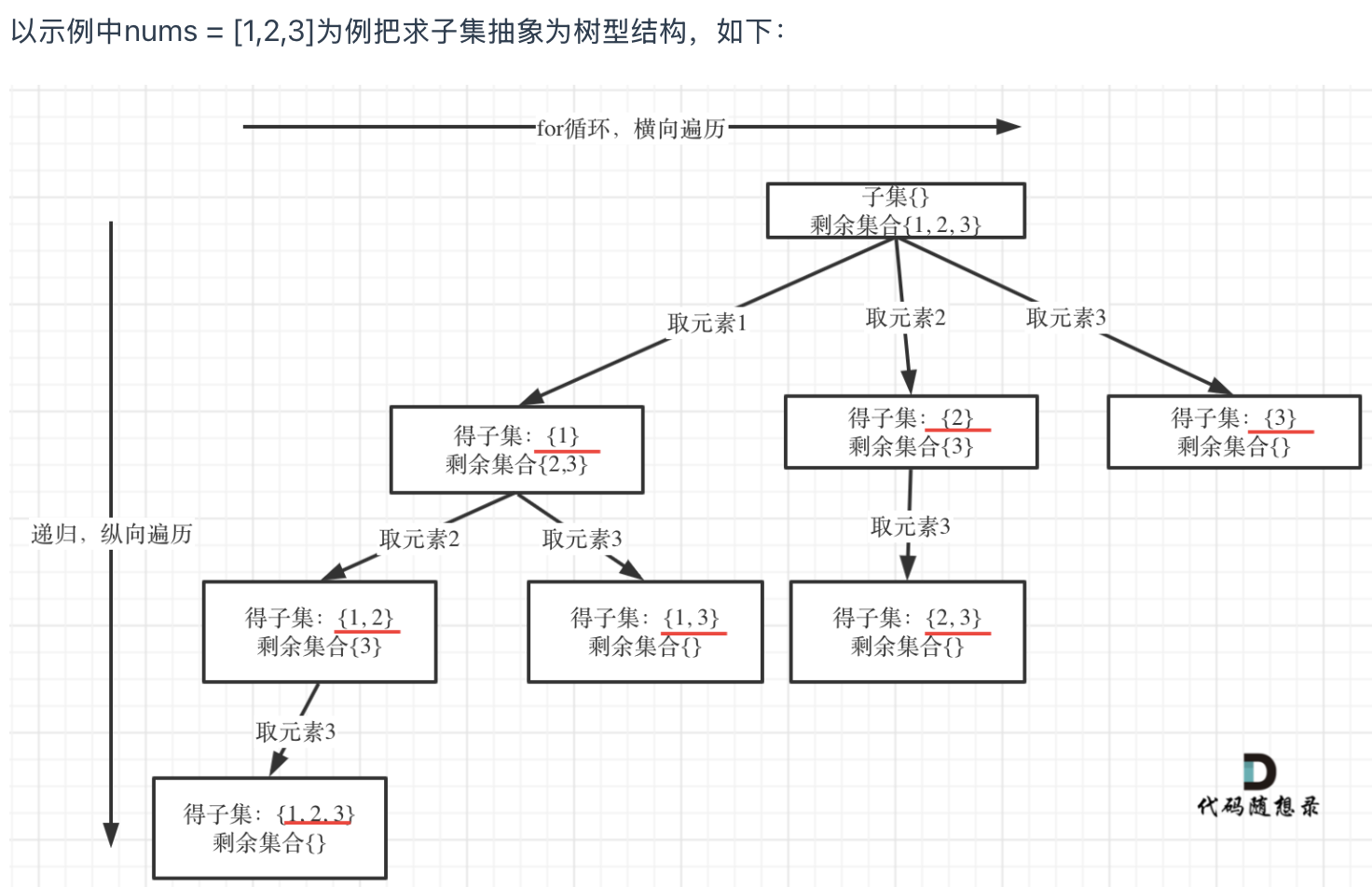
从图中红线部分，可以看出遍历这个树的时候，把所有节点都记录下来，就是要求
的子集集合。

class Solution:
    def backtracking(self, nums, index, path,result):
        if index == len(nums):
            return
        for i in range(index, len(nums)):
            result.append(path+[nums[i]])
            self.backtracking(nums,i+1,path+[nums[i]],result)


    def subsets(self, nums: List[int]) -> List[List[int]]:
        result = [[]]
        self.backtracking(nums,0,[],result)
        return result

90.子集II

大家之前做了 40.组合总和II 和 78.子集 ，本题就是这两道题目的结合，建议自己独立做一做，本题涉及的知识，之前都讲过，没有新内容。

题目链接/文章讲解：https://programmercarl.com/0090.子集II.html
视频讲解：https://www.bilibili.com/video/BV1vm4y1F71J

树枝去重 vs 树层去重

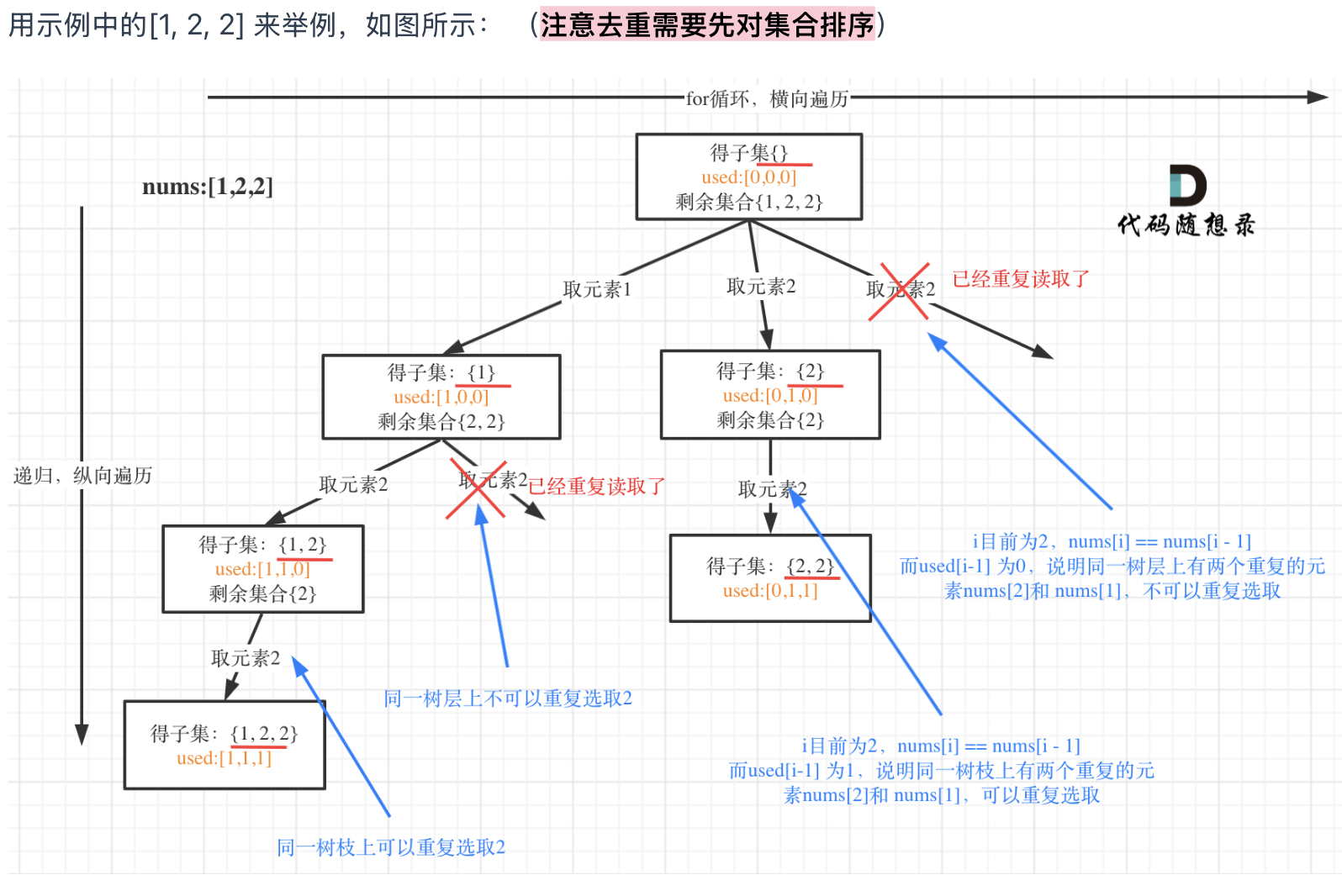
“从图中可以看出，同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集。”

class Solution:
    def backtracking(self,nums,index,path,result):
        if index == len(nums):
            return

        for i in range(index, len(nums)):
            if i > index and nums[i] == nums[i-1]:
                continue
            result.append(path+[nums[i]])
            self.backtracking(nums,i+1,path+[nums[i]],result)


    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        result = [[]]
        self.backtracking(nums,0,[],result)
        return result