代码随想录算法训练营|Day 23
Day 23
第七章 回溯算法part02
39. 组合总和
本题是 集合里元素可以用无数次,那么和组合问题的差别 其实仅在于 startIndex上的控制
题目链接/文章讲解:https://programmercarl.com/0039.组合总和.html
视频讲解:https://www.bilibili.com/video/BV1KT4y1M7HJ
凑合一个版本
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
#宽度 branches:候选
#深度 路径:一个subres
res = []
#cur_sum
def backtracking(candidates, target, index, sub_res, cur_sum):
if cur_sum == target:
res.append(sub_res[:])
return
if cur_sum > target:
return
for i in range(index, len(candidates)):
cur_sum += candidates[i]
backtracking(candidates, target, i, sub_res+[candidates[i]], cur_sum)
cur_sum -= candidates[i]
backtracking(candidates, target, 0, [], 0)
return res
"
本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?
如果是一个集合来求组合的话,就需要startIndex,例如:77.组合 (opens new window),216.组合总和III (opens new window)。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:17.电话号码的字母组合(opens new window)
以上只是说求组合的情况,如果是排列问题,又是另一套分析的套路
"
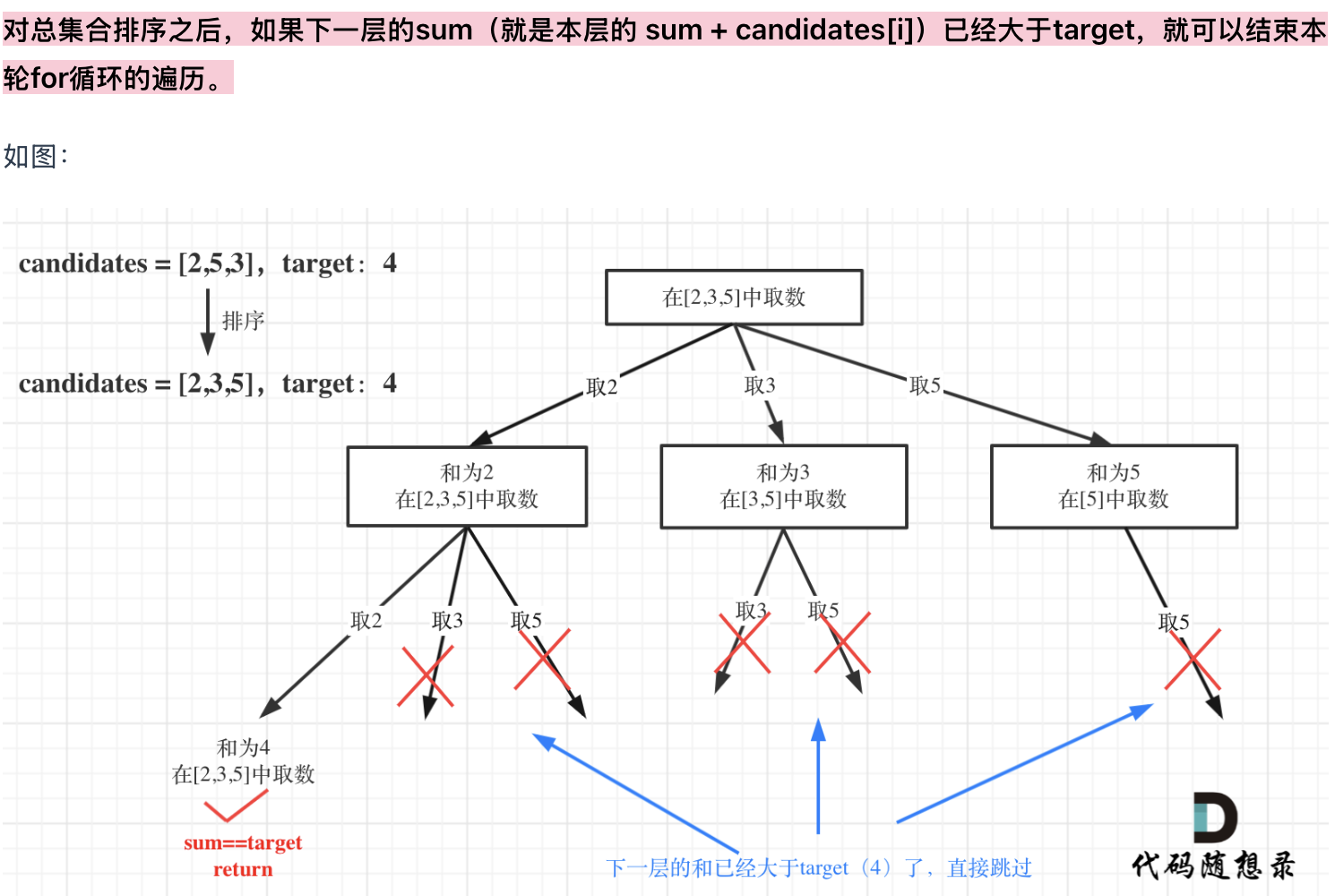
剪枝优化
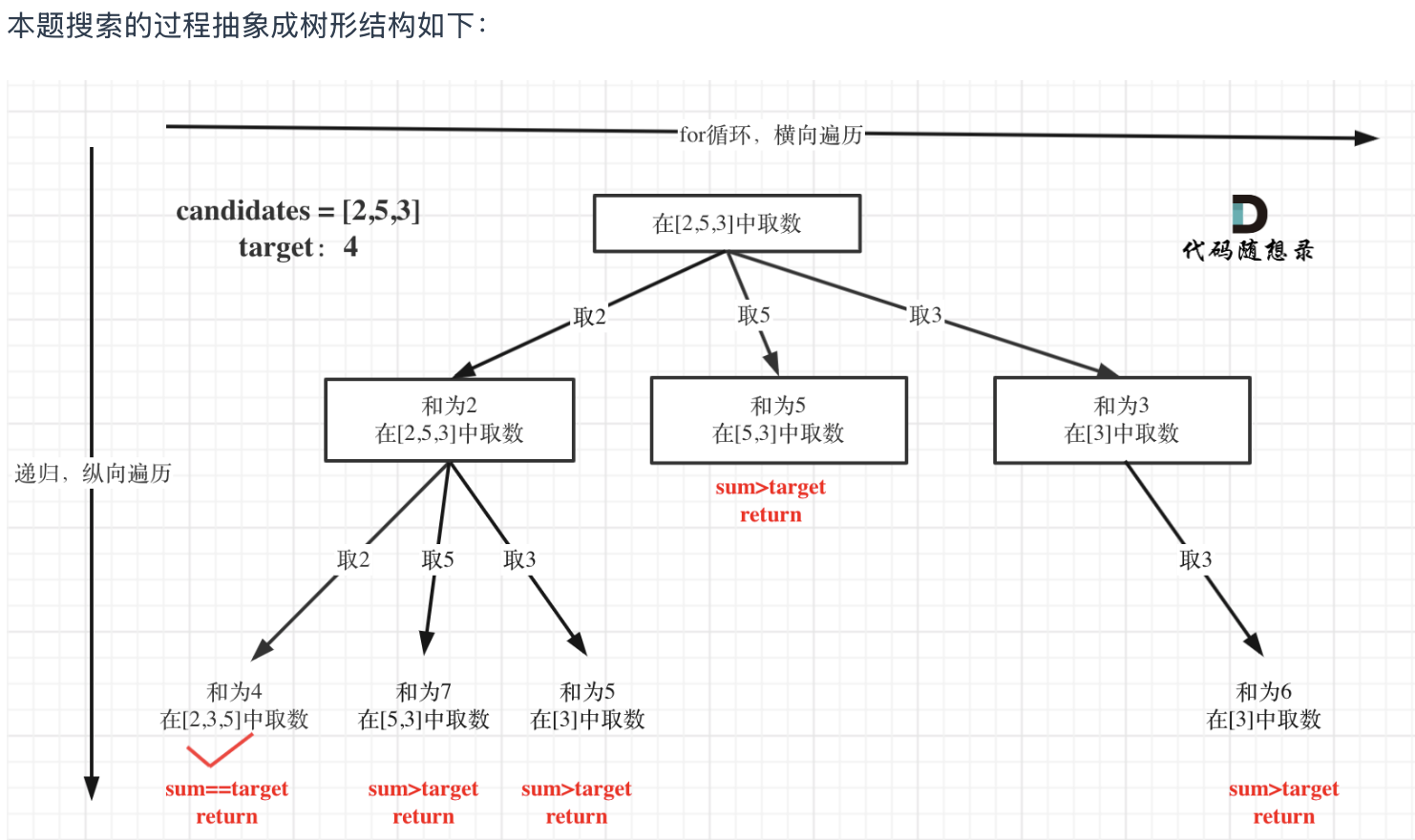
对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
其实如果已经知道下一层的sum会大于target,就没有必要进入下一层递归了。
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
res=[]
candidates.sort()
self.backtracking(candidates,0,0,target,[],res)
return res
def backtracking(self,candidates, start,curr_sum, target_sum,sub_res,res):
if curr_sum == target_sum:
res.append(sub_res[:])
return
for i in range(start, len(candidates)):
if curr_sum + candidates[i] > target_sum:
break
self.backtracking(candidates,i,curr_sum+ candidates[i],target_sum,sub_res+[candidates[i]],res)
40.组合总和II
本题开始涉及到一个问题了:去重。
注意题目中给我们 集合是有重复元素的,那么求出来的 组合有可能重复,但题目要求不能有重复组合。
题目链接/文章讲解:https://programmercarl.com/0040.组合总和II.html
视频讲解:https://www.bilibili.com/video/BV12V4y1V73A
本题难点:
本题的难点在于区别2中:集合(数组candidates)有重复元素,但还不能有重复的组合。
一些同学可能想了:我把所有组合求出来,再用set或者map去重,这么做很容易超时!
所以要在搜索的过程中就去掉重复组合。
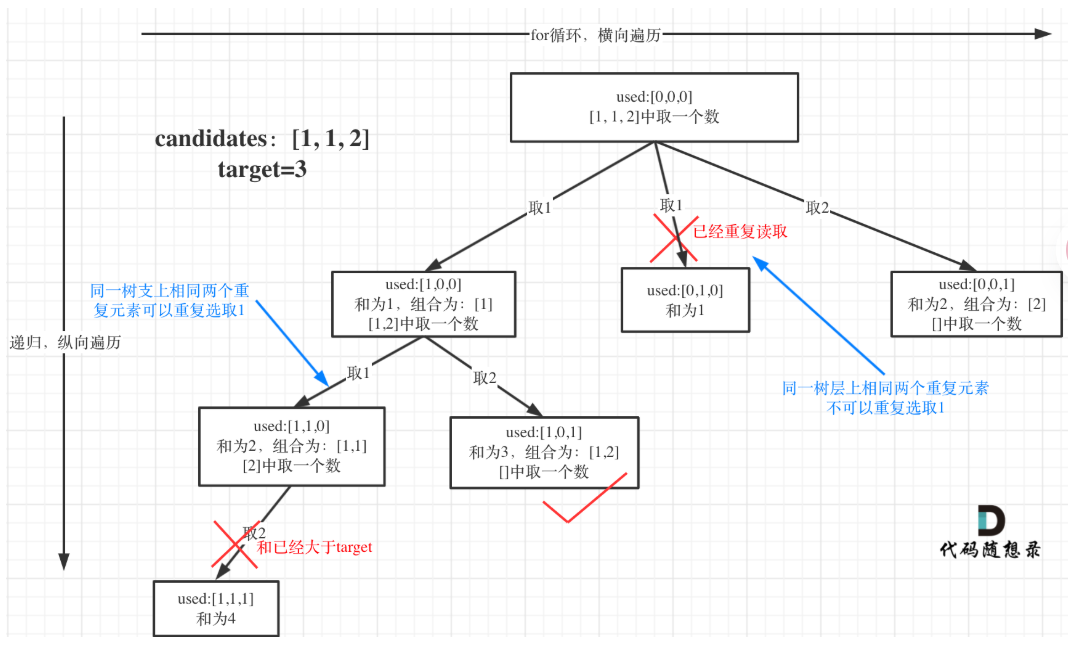
回看一下题目,元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。
所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。
为了理解去重我们来举一个例子,candidates = [1, 1, 2], target = 3,(方便起见candidates已经排序了)
强调一下,树层去重的话,需要对数组排序!
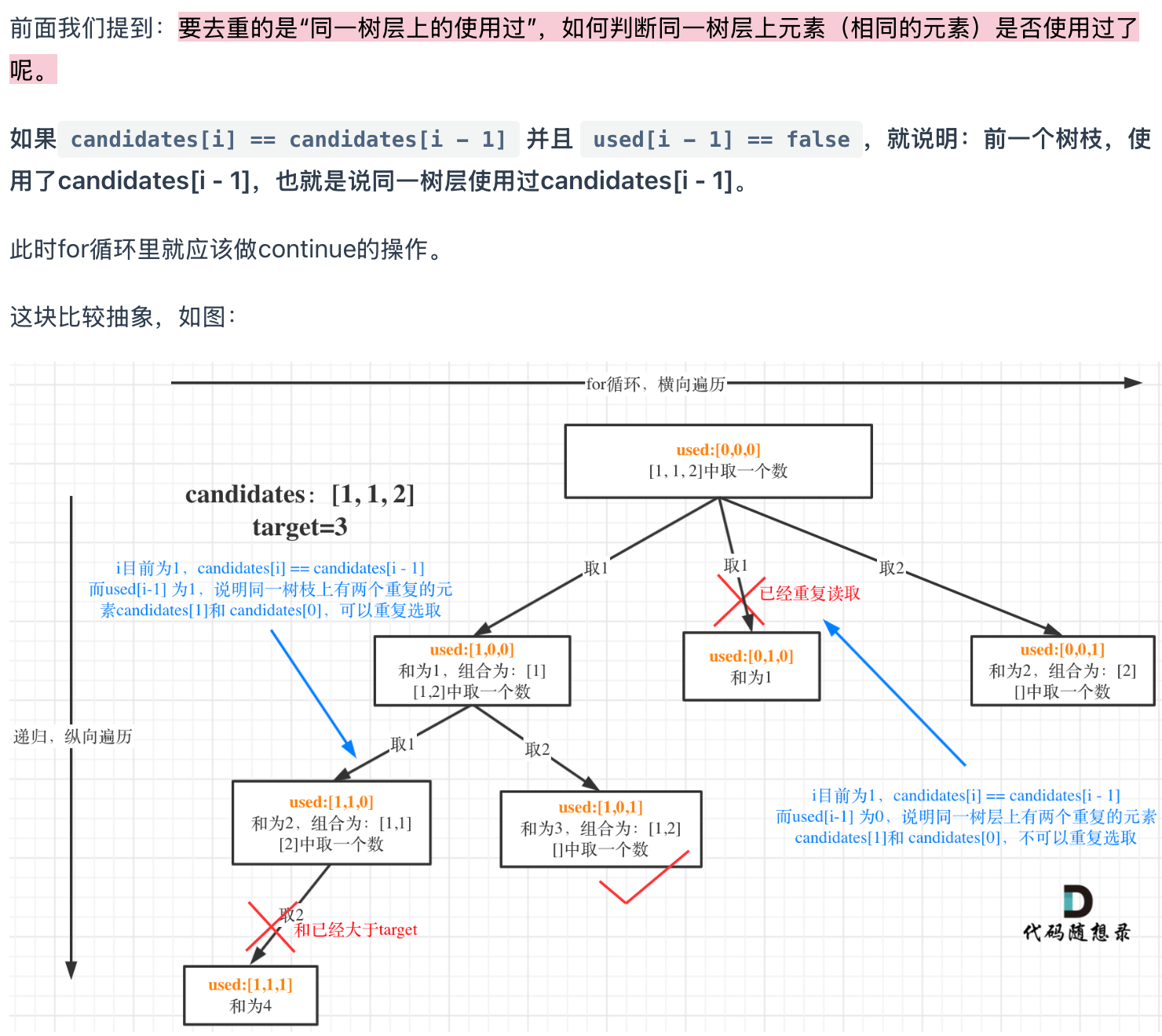
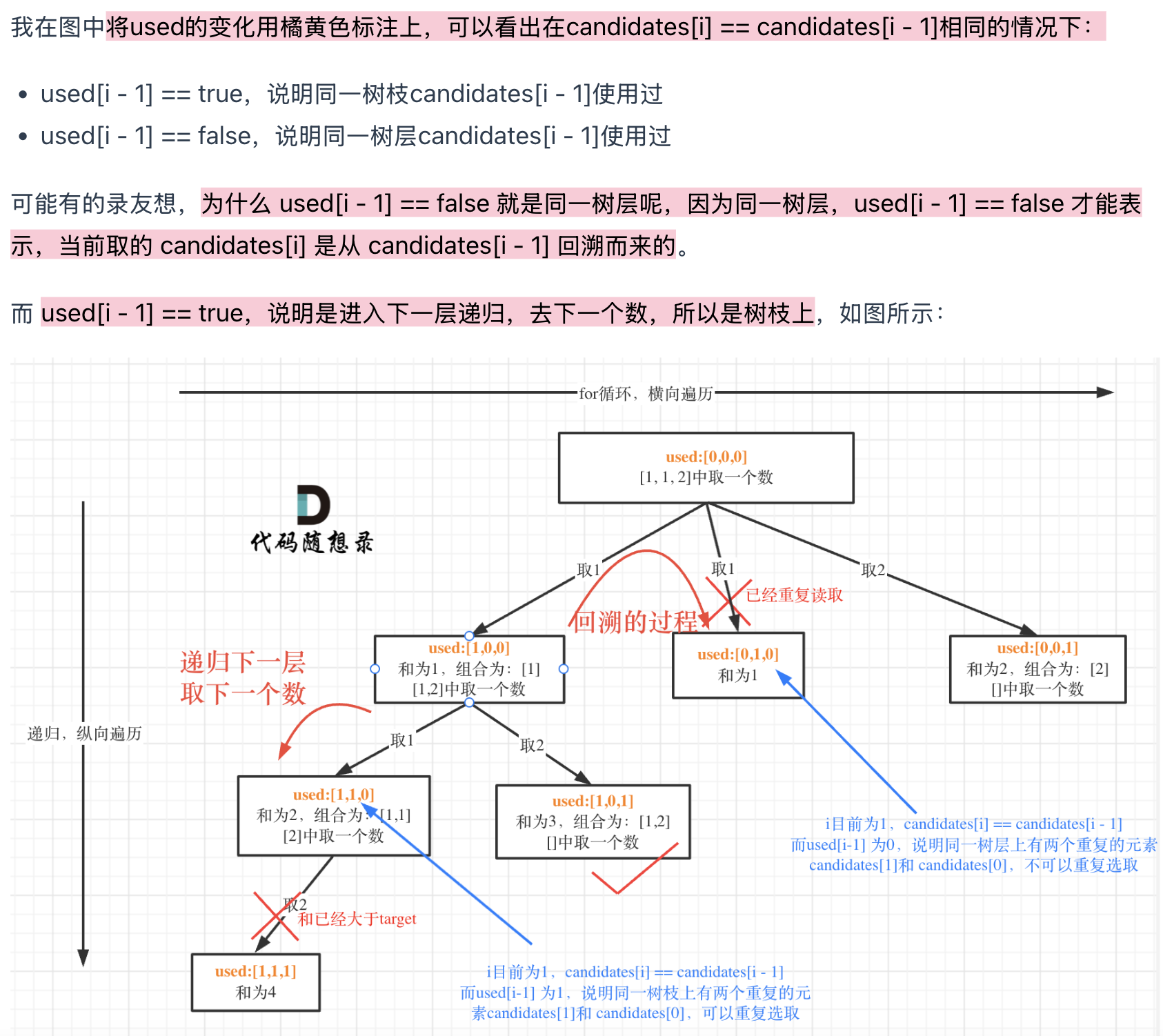
这里直接用startIndex来去重也是可以的, 就不用used数组了。
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
res = []
def _dfs(candidates,target,cur_sum, index, sub_res):
if cur_sum == target:
res.append(sub_res[:])
return
for i in range(index,len(candidates)):
if cur_sum+candidates[i] >target:
break
#同一树层上去重
if i > index and candidates[i] == candidates[i-1]:
continue
_dfs(candidates,target,cur_sum+candidates[i],i+1,sub_res+[candidates[i]])
_dfs(candidates,target,0,0,[])
return res
错点:
_dfs(candidates,target,cur_sum+candidates[i],i+1,sub_res+[candidates[i]])
这句把i+1写成了index+1.....
代码随想录解法
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
results = []
self.combinationSumHelper(candidates, target, 0, [], results)
return results
def combinationSumHelper(self, candidates, target, index, path, results):
if target == 0:
results.append(path[:])
return
for i in range(index, len(candidates)):
if i > index and candidates[i] == candidates[i - 1]:
continue
if candidates[i] > target:
break
path.append(candidates[i])
self.combinationSumHelper(candidates, target - candidates[i], i + 1, path, results)
path.pop()
131.分割回文串
本题较难,大家先看视频来理解 分割问题,明天还会有一道分割问题,先打打基础。
https://programmercarl.com/0131.分割回文串.html
视频讲解:https://www.bilibili.com/video/BV1c54y1e7k6
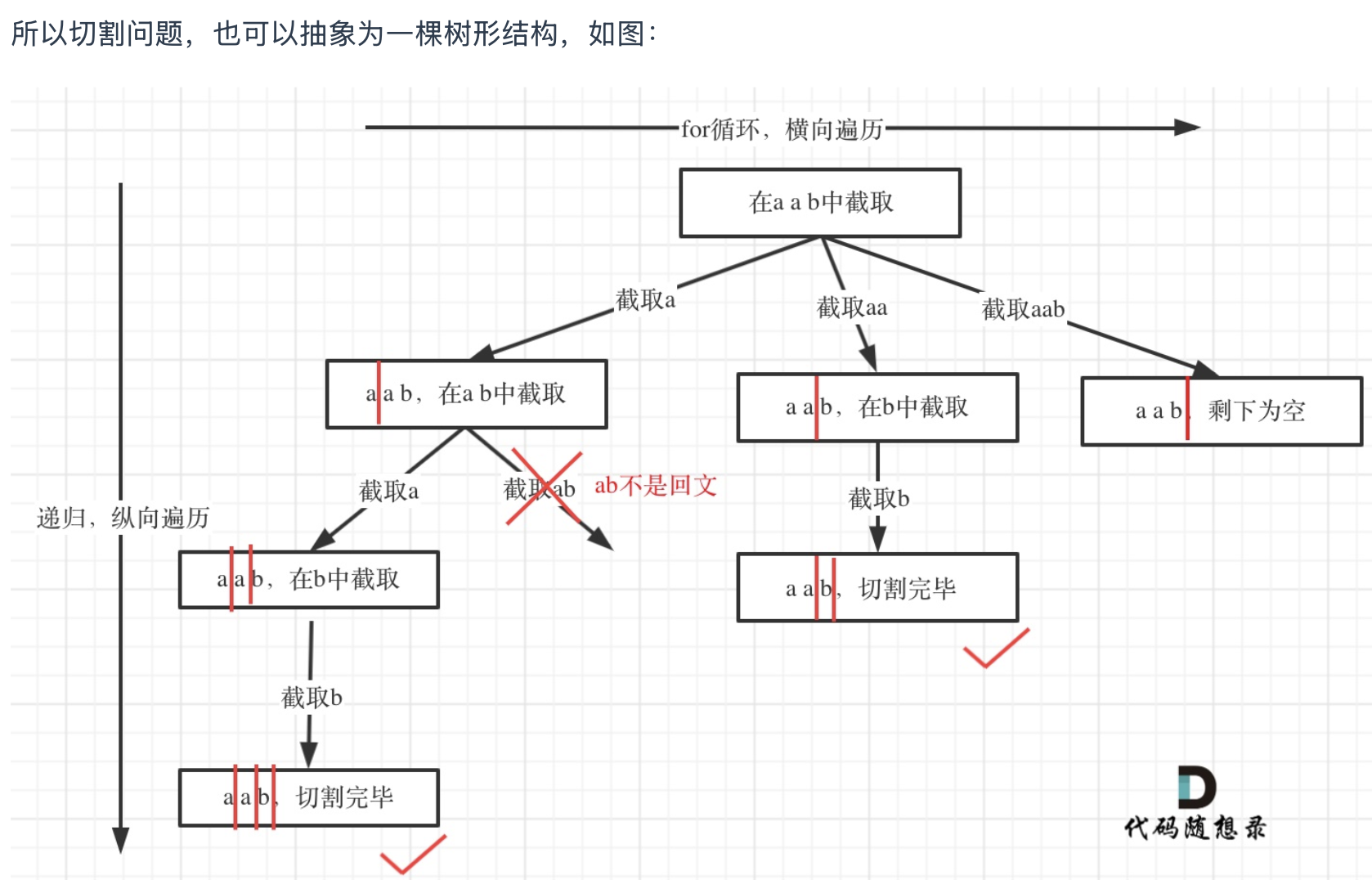
递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
结果都在叶子节点
startIndex是我们切割的线
回溯三部曲
-
递归函数参数
本题递归函数参数需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
-
递归函数终止条件
从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
-
单层搜索的逻辑
在递归循环中如何截取子串呢?
在for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就加入在path中,path用来记录切割过的回文子串。
注意:
切割过的位置,不能重复切割,所以,backtracking(s, i + 1); 传入下一层的起始位置为i + 1
判断回文子串
双指针法

class Solution:
def partition(self, s: str) -> List[List[str]]:
result = []
isPalindrome = [[False] * len(s) for _ in range(len(s))] # 初始化isPalindrome矩阵
self.computePalindrome(s, isPalindrome)
self.backtracking(s, 0, [], result, isPalindrome)
return result
def backtracking(self, s, startIndex, path, result, isPalindrome):
if startIndex >= len(s):
result.append(path[:])
return
for i in range(startIndex, len(s)):
if isPalindrome[startIndex][i]: # 是回文子串
substring = s[startIndex:i + 1]
path.append(substring)
self.backtracking(s, i + 1, path, result, isPalindrome) # 寻找i+1为起始位置的子串
path.pop() # 回溯过程,弹出本次已经添加的子串
def computePalindrome(self, s, isPalindrome):
for i in range(len(s) - 1, -1, -1): # 需要倒序计算,保证在i行时,i+1行已经计算好了
for j in range(i, len(s)):
if j == i:
isPalindrome[i][j] = True
elif j - i == 1:
isPalindrome[i][j] = (s[i] == s[j])
else:
isPalindrome[i][j] = (s[i] == s[j] and isPalindrome[i+1][j-1])
我们一起来完整梳理一下这个 Palindrome Partitioning(分割回文子串) 解法。你写的这份代码其实是「DP 预处理回文 + 回溯枚举分割方案」的经典组合。
问题
给定一个字符串 s,要求把它切分成若干子串,使得每个子串都是回文,返回所有可能的切分。
解法分两部分
1. 预处理 DP 表:isPalindrome
目标:快速判断任意子串 s[i..j] 是否为回文。
isPalindrome = [[False] * len(s) for _ in range(len(s))]
填表逻辑:
-
长度为 1 的子串(
j == i),一定是回文。 -
长度为 2 的子串(
j - i == 1),当s[i] == s[j]时是回文。 -
长度 ≥ 3 的子串,用递推公式:
s[i..j] 是回文 ⇔ s[i] == s[j] 且 s[i+1..j-1] 是回文 -
为什么从后往前计算?
因为要用到isPalindrome[i+1][j-1],所以要保证下一行(更大的 i)已经算好。
这样预处理一次,得到 O(n^2) 的表格,后续查询是否回文就是 O(1)。
2. 回溯搜索所有切分方案
思路:从左到右扫描,每次尝试切出一个回文子串,然后递归处理剩下部分。
def backtracking(s, startIndex, path, result, isPalindrome):
if startIndex == len(s): # 走到末尾
result.append(path[:]) # 保存一条完整切分
return
for i in range(startIndex, len(s)):
if isPalindrome[startIndex][i]: # s[startIndex..i] 是回文
substring = s[startIndex:i+1]
path.append(substring) # 做选择
self.backtracking(s, i+1, path, result, isPalindrome)
path.pop() # 撤销选择(回溯)
关键点:
- 路径 path:保存当前分割结果。
- 边界条件:当起始位置
startIndex == n,说明整串已经分完。 - 选择:尝试每一个
startIndex..i区间,只要是回文就递归。 - 回溯:递归回来后,把刚加入的子串移除,继续尝试其他切法。
举例
输入 s = "aab"
-
初始
startIndex=0-
尝试
"a"(回文) → path = ["a"]
递归到startIndex=1-
尝试
"a"(回文) → path = ["a","a"]
递归到startIndex=2- 尝试
"b"(回文) → path = ["a","a","b"]
递归到末尾 → 加入结果。
- 尝试
-
尝试
"ab"(不是回文) → 跳过。
-
-
尝试
"aa"(回文) → path = ["aa"]
递归到startIndex=2- 尝试
"b"→ path = ["aa","b"]
递归到末尾 → 加入结果。
- 尝试
-
尝试
"aab"(不是回文) → 跳过。
-
最终结果:
[["a","a","b"], ["aa","b"]]
复杂度
- DP 预处理:
O(n^2) - 回溯枚举:最坏情况(字符串全是同一个字符,比如
"aaaa"),回文切分数接近2^(n-1)。 - 所以总复杂度:
O(n^2 + n * 2^n)(由输出规模主导)。
✨ 总结:
- DP 表 isPalindrome 解决「快速判断子串是否回文」。
- 回溯 path 遍历所有可能切分,保证覆盖所有情况。
- 回溯撤销 保证路径正确回退,继续探索其他可能。
回文部分
我就专门帮你拆开「如何判断子串是否回文」这一块,也就是你代码里 computePalindrome 的部分。
基础定义
一个子串 s[i..j] 是回文,当且仅当:
- 首尾相等:
s[i] == s[j],并且 - 中间部分
s[i+1..j-1]也是回文。
特殊情况:
- 长度 1(
i==j):一定回文。 - 长度 2(
j-i==1):只要两个字符相等,就回文。
为什么要用 DP 表 isPalindrome?
如果你每次都临时判断子串是否回文,要扫描一遍字符串,最坏会到 O(n^3)。
所以我们提前用 DP 方式,把所有 s[i..j] 的结果存起来,以后查就是 O(1)。
代码逻辑(你写的版本)
def computePalindrome(self, s, isPalindrome):
for i in range(len(s) - 1, -1, -1): # i 从右往左
for j in range(i, len(s)): # j 从 i 到末尾
if j == i: # 子串只有一个字符
isPalindrome[i][j] = True
elif j - i == 1: # 子串长度=2
isPalindrome[i][j] = (s[i] == s[j])
else: # 长度>=3
isPalindrome[i][j] = (s[i] == s[j] and isPalindrome[i+1][j-1])
为什么 i 要从右往左?
看这一句:
isPalindrome[i][j] = (s[i] == s[j] and isPalindrome[i+1][j-1])
要判断 s[i..j] 是否回文,需要先知道 里面那段 s[i+1..j-1] 是否回文。
而 i+1 > i,所以必须保证在计算 (i,j) 之前,已经算过 (i+1,j-1)。
因此 i 要从大到小循环。
举个例子:s = "aba"
-
长度=1:
isPalindrome[0][0] = True("a")isPalindrome[1][1] = True("b")isPalindrome[2][2] = True("a")
-
长度=2:
isPalindrome[0][1] = (s[0]==s[1]) = (a==b)=FalseisPalindrome[1][2] = (s[1]==s[2]) = (b==a)=False
-
长度=3:
isPalindrome[0][2] = (s[0]==s[2]) and isPalindrome[1][1]
=(a==a) and True = True
最后表格是:
0 1 2
0 [T, F, T]
1 [ , T, F]
2 [ , , T]
意思是:
- "a"(0..0) 回文
- "b"(1..1) 回文
- "a"(2..2) 回文
- "aba"(0..2) 回文 ✅
我们用同一个例子 s = "abba",把 computePalindrome 里两层循环的 i、j 变化过程逐步“走表”。
外层:i 从右到左(3 → 0)
内层:j 从 i 到末尾(i → 3)
为了直观,每一步我都写出:区间、长度、规则与结果。
准备
s = a b b a
0 1 2 3 (下标)
规则速记:
- 长度1:True
- 长度2:
s[i]==s[j] - 长度≥3:
s[i]==s[j] and isPalindrome[i+1][j-1]
逐步填表日志(i,j 的变化)
i = 3
- (i=3, j=3) ⇒ 区间 s[3..3] = "a",长度1 → True
P[3][3]=True
i = 2
- (2,2) ⇒ "b",长度1 → True
P[2][2]=True - (2,3) ⇒ "ba",长度2 → 比较
s[2]=='b'vss[3]=='a'→ False
P[2][3]=False
i = 1
- (1,1) ⇒ "b",长度1 → True
P[1][1]=True - (1,2) ⇒ "bb",长度2 →
s[1]=='b'vss[2]=='b'→ True
P[1][2]=True - (1,3) ⇒ "bba",长度3 → 首尾
bvsa不等 → False(无需看内层)
P[1][3]=False
i = 0
- (0,0) ⇒ "a",长度1 → True
P[0][0]=True - (0,1) ⇒ "ab",长度2 →
avsb→ False
P[0][1]=False - (0,2) ⇒ "abb",长度3 → 首尾
avsb不等 → False
P[0][2]=False - (0,3) ⇒ "abba",长度4
- 首尾相等:
s[0]==s[3](a==a)✅ - 查内层回文:
P[1][2]之前在步骤 5 已算出 True
⇒P[0][3] = True and True = True
关键依赖:(0,3) 需要 (1,2),而 (1,2) 是在
i=1时已计算好——这就是为什么i必须从右往左。
最终 DP 表 P = isPalindrome
(行是 i,列是 j)
j=0 j=1 j=2 j=3
i=0 [ T , F , F , T ]
i=1 [ , T , T , F ]
i=2 [ , , T , F ]
i=3 [ , , , T ]
表意:
- 单字符全回文;
"bb"(1..2)回文;"abba"(0..3)回文;- 其他区间非回文。
如果你把上面的 10 个步骤照着自己的代码在纸上跑一遍,就能完全理解:
i从右到左是为了解决P[i+1][j-1]的依赖;j从左到右保证同一行从短到长推进;- 三种长度规则覆盖了所有情况。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号