代码随想录算法训练营|Day 21
Day 21
第六章 二叉树part08
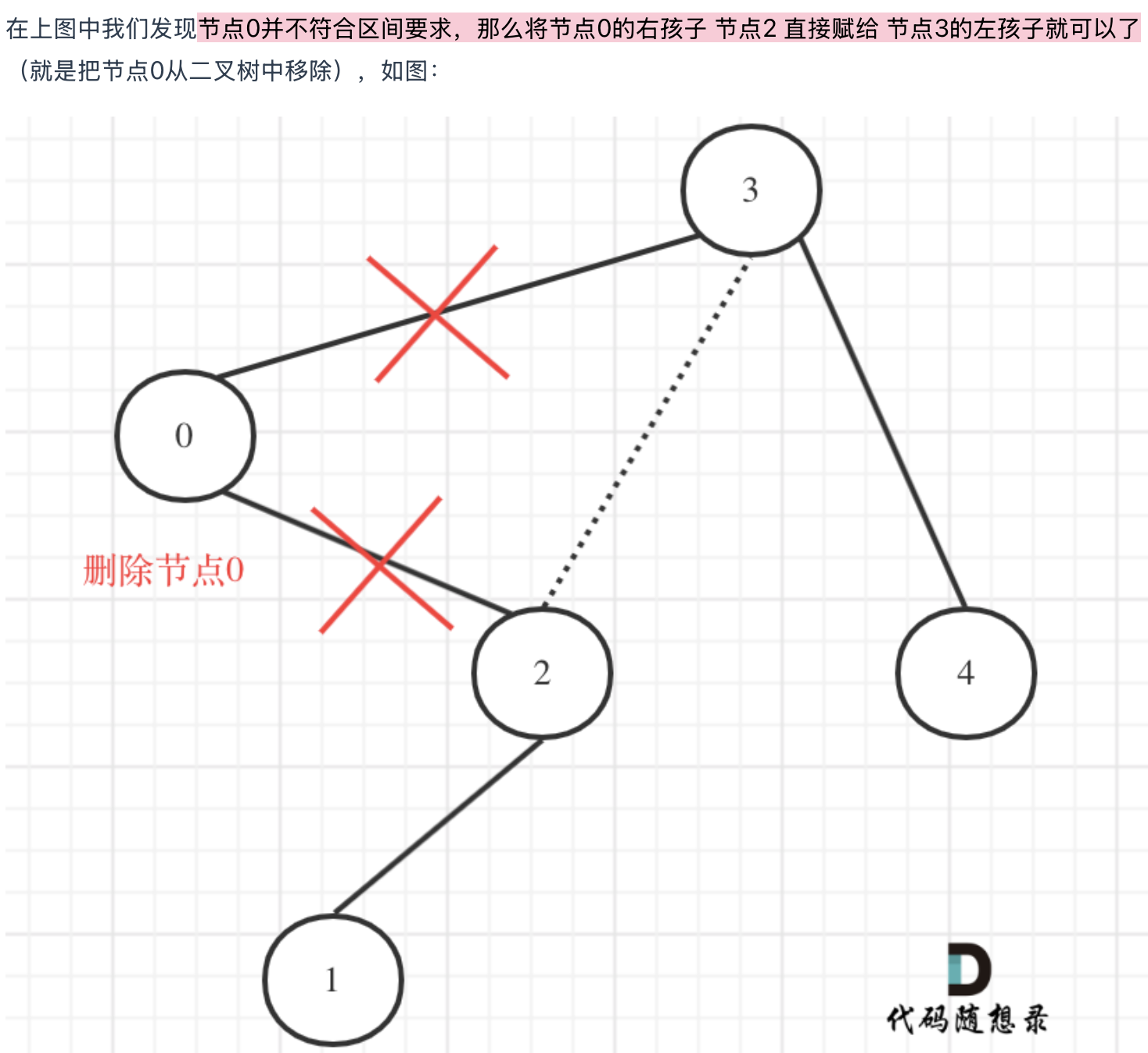
669. 修剪二叉搜索树
这道题目比较难,比 添加增加和删除节点难的多,建议先看视频理解。
题目链接/文章讲解: https://programmercarl.com/0669.修剪二叉搜索树.html
视频讲解: https://www.bilibili.com/video/BV17P41177ud
按照第二十天的删节点思路仿写
class Solution:
def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:
if root is None:
return root
if low <= root.val <= high:
root.left = self.trimBST(root.left, low, high)
root.right = self.trimBST(root.right, low, high)
return root #这一句开始没写一直报错
else:
if root.left is None and root.right is None:
return None
elif root.left is None:
return self.trimBST(root.right, low, high)
elif root.right is None:
return self.trimBST(root.left,low,high)
else:
cur = root.right
while cur.left:
cur = cur.left
cur.left = root.left
return self.trimBST(root.right, low,high)
更有逻辑的思路
递归法


class Solution:
def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
if root is None:
return None
if root.val > high:
return self.trimBST(root.left, low, high)
if root.val < low:
return self.trimBST(root.right, low, high)
root.left = self.trimBST(root.left, low, high)
root.right = self.trimBST(root.right, low, high)
return root
迭代法
class Solution:
def trimBST(self, root: TreeNode, L: int, R: int) -> TreeNode:
if not root:
return None
# 处理头结点,让root移动到[L, R] 范围内,注意是左闭右闭
while root and (root.val < L or root.val > R):
if root.val < L:
root = root.right # 小于L往右走
else:
root = root.left # 大于R往左走
cur = root
# 此时root已经在[L, R] 范围内,处理左孩子元素小于L的情况
while cur:
while cur.left and cur.left.val < L:
cur.left = cur.left.right
cur = cur.left
cur = root
# 此时root已经在[L, R] 范围内,处理右孩子大于R的情况
while cur:
while cur.right and cur.right.val > R:
cur.right = cur.right.left
cur = cur.right
return root
好,这个写法是 迭代版的 trimBST,思路和递归是一样的,只不过不用函数栈,而是用 while 循环一步步把指针调整过来。我们拆开来看:
1. 处理根节点不在区间 [L, R] 的情况
while root and (root.val < L or root.val > R):
if root.val < L:
root = root.right # 小于L,丢掉左子树,去右子树
else:
root = root.left # 大于R,丢掉右子树,去左子树
-
因为 BST 的性质:
- 如果
root.val < L,整棵左子树都 < L,不可能有合法节点 → 根往右走。 - 如果
root.val > R,整棵右子树都 > R,不可能有合法节点 → 根往左走。
- 如果
-
这个循环保证最终停下来的
root一定在[L, R]内(或者是 None)。
2. 修剪左子树里过小的节点
cur = root
while cur:
while cur.left and cur.left.val < L:
cur.left = cur.left.right
cur = cur.left
逻辑:
-
从根开始,一路向左。
-
每次检查当前节点的左孩子:
- 如果
cur.left.val < L,说明这个左孩子和它的整个左子树都比 L 小 → 都要删掉。 - 但是它的右子树可能还有合法节点(值可能 ≥ L),所以直接把
cur.left替换为cur.left.right。
- 如果
-
然后继续往下走,直到走到最左端。
3. 修剪右子树里过大的节点
cur = root
while cur:
while cur.right and cur.right.val > R:
cur.right = cur.right.left
cur = cur.right
逻辑类似:
-
从根开始,一路向右。
-
每次检查当前节点的右孩子:
- 如果
cur.right.val > R,说明这个右孩子和它的整个右子树都比 R 大 → 都要删掉。 - 但是它的左子树可能还有合法节点(值可能 ≤ R),所以直接把
cur.right替换为cur.right.left。
- 如果
-
然后继续往右端走。
4. 返回结果
最后返回调整过的 root,它就是修剪后的合法 BST。
🔑 总结一下思路
- 第一步:把
root移动到合法区间[L, R]内。 - 第二步:从根往左走,修剪掉所有
< L的左子树。 - 第三步:从根往右走,修剪掉所有
> R的右子树。 - 利用 BST 性质:一次走就能处理掉整片无效子树。
好,我们用一个具体的小树来演示一下迭代法的过程。假设有一棵 BST:
4
/ \
2 6
/ \ / \
1 3 5 7
要修剪到区间 [3, 6]。
第一步:找到合法的 root
while root and (root.val < L or root.val > R):
- 初始
root = 4,4 ∈ [3,6],所以直接停下。
✔️ 最终 root 仍然是4。
第二步:修剪左子树里 < L 的部分
左子树是:
2
/ \
1 3
从根 cur = 4 往左走:
-
cur = 4,检查cur.left = 2,2 < 3❌,所以:cur.left = cur.left.right→
cur.left从2变成3。树变成:
4 / \ 3 6 / \ 5 7 -
接下来
cur = 3,它的left = None,循环结束。
✔️ 左子树修剪完成。
第三步:修剪右子树里 > R 的部分
右子树是:
6
/ \
5 7
从根 cur = 4 往右走:
-
cur = 4,检查cur.right = 6,6 ∈ [3,6]✅,不用动,往下走。 -
cur = 6,检查cur.right = 7,7 > 6❌,所以:cur.right = cur.right.left但
7.left = None,所以直接把cur.right设为None。树变成:
4 / \ 3 6 / 5 -
接下来
cur = 6.right = None,循环结束。
✔️ 右子树修剪完成。
最终结果
修剪后的树就是:
4
/ \
3 6
/
5
其中所有节点值都在 [3,6] 范围内。
108.将有序数组转换为二叉搜索树
本题就简单一些,可以尝试先自己做做。
https://programmercarl.com/0108.将有序数组转换为二叉搜索树.html
视频讲解:https://www.bilibili.com/video/BV1uR4y1X7qL
递归法
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
if not nums:
return None
mid = len(nums)//2
root = TreeNode(nums[mid])
left = nums[:mid]
right = nums[mid+1:]
root.left = self.sortedArrayToBST(left)
root.right = self.sortedArrayToBST(right)
return root

迭代法
存一下下次再看
from collections import deque
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
if len(nums) == 0:
return None
root = TreeNode(0) # 初始根节点
nodeQue = deque() # 放遍历的节点
leftQue = deque() # 保存左区间下标
rightQue = deque() # 保存右区间下标
nodeQue.append(root) # 根节点入队列
leftQue.append(0) # 0为左区间下标初始位置
rightQue.append(len(nums) - 1) # len(nums) - 1为右区间下标初始位置
while nodeQue:
curNode = nodeQue.popleft()
left = leftQue.popleft()
right = rightQue.popleft()
mid = left + (right - left) // 2
curNode.val = nums[mid] # 将mid对应的元素给中间节点
if left <= mid - 1: # 处理左区间
curNode.left = TreeNode(0)
nodeQue.append(curNode.left)
leftQue.append(left)
rightQue.append(mid - 1)
if right >= mid + 1: # 处理右区间
curNode.right = TreeNode(0)
nodeQue.append(curNode.right)
leftQue.append(mid + 1)
rightQue.append(right)
return root
deque回顾
1. deque 是什么?
- 来自
collections模块:from collections import deque - 是 双端队列(double-ended queue)
- 支持在队列两端 O(1) 插入和删除
- 常用在 BFS、滑动窗口、迭代树构造等场景
2. 常用方法
from collections import deque
q = deque() # 初始化空队列
q.append(1) # 在右端添加元素 -> [1]
q.append(2) # [1, 2]
q.appendleft(0) # 在左端添加 -> [0, 1, 2]
x = q.pop() # 从右端取出并删除 -> 返回2, q = [0, 1]
y = q.popleft() # 从左端取出并删除 -> 返回0, q = [1]
print(q) # deque([1])
append()→ 右边入队appendleft()→ 左边入队pop()→ 右边出队popleft()→ 左边出队
3. 为什么用 deque 而不是 list?
Python 的 list 做 左端删除(pop(0))是 O(n),因为要整体移动元素。
而 deque 专门优化了两端操作,popleft() 是 O(1)。
👉 所以 BFS、层序遍历、迭代建树时都推荐 deque。
4. 在你那段迭代建树代码里的作用
回到你 sortedArrayToBST 的迭代解法:
nodeQue = deque()
leftQue = deque()
rightQue = deque()
这 3 个队列是一一对应的:
nodeQue:当前要赋值的节点leftQue、rightQue:该节点对应的数组区间
运行时,每次循环:
curNode = nodeQue.popleft()
left = leftQue.popleft()
right = rightQue.popleft()
👉 从队列左边取出“一组任务”。
然后处理完后(确定中点、建立左右子节点),再用 append() 把子任务丢到队尾,等待后续处理。
这就是典型的 BFS 队列调度。
5. 小练习帮你熟悉
你可以自己跑一下这个小例子:
from collections import deque
q = deque()
q.append("root") # 加入root任务
q.append("left") # 加入left任务
q.append("right") # 加入right任务
print(q) # deque(['root', 'left', 'right'])
print(q.popleft()) # 出队 -> root
print(q) # deque(['left', 'right'])
q.append("new") # 加入新任务
print(q) # deque(['left', 'right', 'new'])
你会发现:
- 它就是一个普通队列:先进先出(FIFO)。
- 我们只是在 BFS 建树里多用了几条平行队列(保存节点对象、保存左右区间)。
这个写法其实就是把递归过程手动展开成了 BFS(层序)迭代。我们一步步看:
🌱 递归版回顾
递归版的思路是:
- 找中点
mid,建立根节点。 - 递归处理左半部分 → 左子树。
- 递归处理右半部分 → 右子树。
迭代法要做的,就是用队列自己管理这些“待处理的区间”。
🌳 迭代版的三个队列
代码里用了三个队列:
nodeQue:保存正在等待赋值的节点。leftQue、rightQue:保存该节点对应的子数组区间范围 [left, right]。
这样就把“递归里传下去的参数”显式存在队列里了。
🔄 核心循环
while nodeQue:
curNode = nodeQue.popleft()
left = leftQue.popleft()
right = rightQue.popleft()
mid = left + (right - left) // 2
curNode.val = nums[mid]
- 从队列里拿出一个“任务”:一个节点 + 区间
[left, right]。 - 找到该区间的中点
mid,把值nums[mid]赋给当前节点。 - 这一步等价于递归里的“确定根节点”。
👈 处理左半部分
if left <= mid - 1:
curNode.left = TreeNode(0) # 占位节点
nodeQue.append(curNode.left)
leftQue.append(left)
rightQue.append(mid - 1)
- 如果左区间
[left, mid-1]非空,就说明有左子树。 - 建一个占位
TreeNode(0)挂上去。 - 把它和对应的区间放进队列 → 等待后续处理。
👉 处理右半部分
if right >= mid + 1:
curNode.right = TreeNode(0)
nodeQue.append(curNode.right)
leftQue.append(mid + 1)
rightQue.append(right)
逻辑同理,对右区间 [mid+1, right] 建立右子树。
🏁 循环终止
当所有区间都处理完,队列为空,树就构建好了。
⚖️ 举个例子
假设 nums = [-10, -3, 0, 5, 9]
-
初始:
root(0)+ 区间[0, 4]入队。 -
出队
(root, 0, 4)→mid=2,root.val = 0。- 左子区间
[0,1]→ 建立左孩子。 - 右子区间
[3,4]→ 建立右孩子。
- 左子区间
-
出队
(root.left, 0, 1)→mid=0,值-10。- 右子区间
[1,1]→ 建立右孩子-3。
- 右子区间
-
出队
(root.right, 3, 4)→mid=3,值5。- 右子区间
[4,4]→ 建立右孩子9。
- 右子区间
-
队列空,完成。
最终树结构:
0
/ \
-10 5
\ \
-3 9
✅ 总结
-
递归版:函数栈帮我们保存“子区间”任务。
-
迭代版:用三个队列手动保存“任务”:
- 节点本身
- 对应区间
[left, right]
-
每次循环处理一个任务,逐层扩展子树。
这样做的好处:
- 不会因为递归太深导致栈溢出。
- 思路清晰:和 BFS 构建树类似。
538.把二叉搜索树转换为累加树
本题也不难,在 求二叉搜索树的最小绝对差 和 众数 那两道题目 都讲过了 双指针法,思路是一样的。
https://programmercarl.com/0538.把二叉搜索树转换为累加树.html
视频讲解:https://www.bilibili.com/video/BV1d44y1f7wP
尝试做
class Solution:
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
#对于一个节点
# 身为左树 且 >=其值 的之和的:本身 + 已构造新树的其父节点的值+其右树的值
# 身为右树 且 >=其值 的之和的:本身 + 其右树的值
#思路:先构造右树,再构造左树
#遍历顺序:右中左
if root.right is not None:
root.right = self.convertBST(root.right)
root.val += root.right.val
if root.left is not None:
root.left = self.convertBST(root.left)
root.left.val += root.val
return root
你这题的关键是:不要把“该加多少”寄存在子节点的 val 里,然后往上拼。正确做法是用右→中→左(reverse in-order)遍历,并维护一个全局/闭包的累加和 acc:走到当前节点时,它右边的节点都已经访问过,acc 就是“所有 ≥ 它的值的和(包含它自己之前的和)”。于是:
- 先遍历右子树,累加更大的值到
acc - 再把当前节点的值更新为
acc += 原值 - 最后去遍历左子树
你这版为什么不对?
你写的是:
if root.right is not None:
root.right = self.convertBST(root.right)
root.val += root.right.val # 用右子树根的 val 作为“右边之和”
if root.left is not None:
root.left = self.convertBST(root.left)
root.left.val += root.val # 只把父节点的值加到“左孩子根”
两个核心问题:
-
root.val += root.right.val错因:root.right.val在转换后表示“≥ 右孩子原值的和”,**并不等于“整棵右子树所有原值之和”**的稳定载体(逻辑上容易混淆,特别是有更深层结构或重复值时就不正确)。 -
root.left.val += root.val只给“左子树的根”加了父节点的贡献,左子树更深层的节点完全没得到来自父节点与其右侧的贡献,导致左子树内部的很多节点都偏小。
反例(你这版会错)
5
/
2
/
1
正确答案(≥ 节点值的和)应为:
- 5→5
- 2→7(=2+5)
- 1→8(=1+2+5)
你的流程会把 1 只加到 3(=1+2),没有加上来自根 5 的贡献。
小结
- 反向中序遍历(Right→Node→Left)保证访问顺序是从大到小;
- 用一个
acc把“已经处理过的更大节点之和”带着走; - 更新时:
acc += node.val; node.val = acc; - 不要尝试用“子树根的值”来代替右侧总和,也不要只给“左孩子根”加父节点,深层节点会漏算。
递归法
class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
self.pre = 0 # 记录前一个节点的数值
self.traversal(root)
return root
def traversal(self, cur):
if cur is None:
return
self.traversal(cur.right)
cur.val += self.pre
self.pre = cur.val
self.traversal(cur.left)
迭代法
class Solution:
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return root
stack = []
cur = root
pre = 0
while cur or stack:
if cur:
stack.append(cur)
cur = cur.right
else:
cur = stack.pop()
cur.val+= pre
pre = cur.val
cur =cur.left
return root
总结篇
好了,二叉树大家就这样刷完了,做一个总结吧





 浙公网安备 33010602011771号
浙公网安备 33010602011771号