代码随想录算法训练营|Day 18

Day 18

第六章 二叉树part06

详细布置

530.二叉搜索树的最小绝对差

需要领悟一下二叉树遍历上双指针操作，优先掌握递归
题目链接/文章讲解：https://programmercarl.com/0530.二叉搜索树的最小绝对差.html
视频讲解：https://www.bilibili.com/video/BV1DD4y11779

暴力写法

中序遍历 将二叉搜索树转化为有序数组

遍历有序数组，计算相邻两个节点最小的差值

中序遍历 双指针 不转换为数组

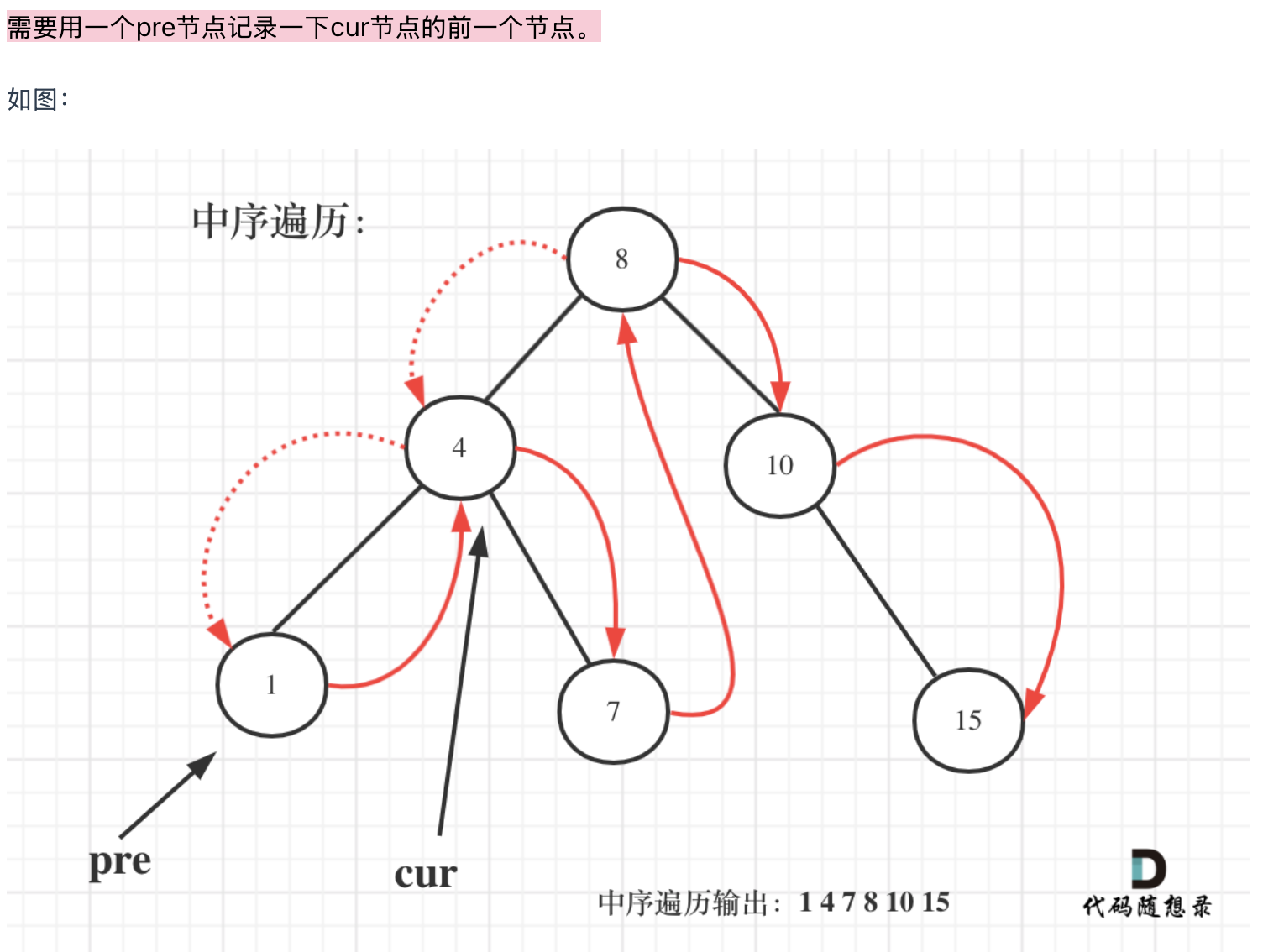
递归法
res 记录相邻节点差值的最小值

class Solution:
    def __init__(self):
        self.res = float('inf')
        self.pre = None

    def traversal(self, cur):
        if cur is None:
            return
        self.traversal(cur.left)
        if self.pre is not None:
            self.res = min(self.res, cur.val - self.pre.val)
        self.pre = cur
        self.traversal(cur.right)
    def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
        self.traversal(root)
        return self.res

迭代法

class Solution:
    def getMinimumDifference(self, root):
        stack = []
        cur = root
        pre = None
        result = float('inf')

        while cur is not None or len(stack) > 0:
            if cur is not None:
                stack.append(cur)  # 将访问的节点放进栈
                cur = cur.left  # 左
            else:
                cur = stack.pop()
                if pre is not None:  # 中
                    result = min(result, cur.val - pre.val)
                pre = cur
                cur = cur.right  # 右

        return result

501.二叉搜索树中的众数

和 530差不多双指针思路，不过 这里涉及到一个很巧妙的代码技巧。

可以先自己做做看，然后看我的视频讲解。

https://programmercarl.com/0501.二叉搜索树中的众数.html
视频讲解：https://www.bilibili.com/video/BV1fD4y117gp

普通二叉树

递归法，利用字典

from collections import defaultdict

class Solution:
    def searchBST(self, cur, freq_map):
        if cur is None:
            return
        freq_map[cur.val] += 1  # 统计元素频率
        self.searchBST(cur.left, freq_map)
        self.searchBST(cur.right, freq_map)

    def findMode(self, root):
        freq_map = defaultdict(int)  # key:元素，value:出现频率
        result = []
        if root is None:
            return result
        self.searchBST(root, freq_map)
        max_freq = max(freq_map.values())
        for key, freq in freq_map.items():
            if freq == max_freq:
                result.append(key)
        return result

二叉搜索树

中序遍历时，元素才是有序的，单调递增的
递归法，利用BST性质

class Solution:
    def __init__(self):
        self.maxCnt = 0  # 最大频率
        self.cnt = 0 # 统计频率
        self.pre = None
        self.res = []

    def searchBST(self,cur):
        if cur is None:
            return

        searchBST(cur.left) # 左

        # 中
        if self.pre is None: #第一个节点
            self.cnt = 1
        elif self.pre.val == cur.val:
            self.cnt += 1
        else:
            #与前一个节点数值不同
            self.cnt = 1
        self.pre = cur #更新节点

        #与最大值频率相同，放入结果数组
        if self.cnt == self.maxCnt:
            self.res.append(cur.val)

        #若计数大于最大值频率，就更新最大频率
        #记得清空res，之前res里的元素均失效
        if self.cnt > self.maxCnt: 
            self.maxCnt = self.cnt
            self.res = [cur.val]
        
        
        self.searchBST(cur.right) #右
        return
    
    def findMode(self,root):
        self.cnt = 0
        self.maxCnt = 0
        self.pre = None
        self.res= []

        self.searchBST(root)

        return self.res

如果先比较计数频率是否大于maxCnt:

if self.cnt > self.maxCnt:
    self.maxCnt = self.cnt
    self.res = [cur.val]
if self.cnt == self.maxCnt:
    self.res.append(cur.val)

当出现“新的更大频次”时（self.cnt > self.maxCnt），你先把 res 设为 [cur.val]，
但紧接着第二个 if 也成立（因为此时 self.cnt == self.maxCnt 了），又把同一个值 append 一次，导致同元素被加入两次。

修正

把第二个判断改成 elif，只在“没有出现更大频次、但与最大频次相等”时追加：

if self.cnt > self.maxCnt:
    self.maxCnt = self.cnt
    self.res = [cur.val]      # 发现更大频次，重置结果为当前值
elif self.cnt == self.maxCnt:
    self.res.append(cur.val)  # 频次相同，追加

其余逻辑保持不变即可。

小例子直观理解

假设第一次遇到值 2：

• 计数 cnt 从 0 到 1，maxCnt 原本是 0。
• 进入 cnt > maxCnt 分支：res = [2]。
• 这时 cnt == maxCnt 也成立，如果是第二个独立 if 又追加一次 → [2, 2]（重复）。
• 用 elif 就不会再追加。

---

---

1. __init__ 里的初始化

def __init__(self):
    self.maxCount = 0  # 最大频率
    self.count = 0     # 当前值的频率
    self.pre = None    # 前一个节点
    self.result = []   # 保存结果

这是对象第一次创建时的初始化。

• 也就是说你在外面 sol = Solution() 时，这些成员变量都会被设置好。
• 但注意：这只是“构造时”的一次性设置，并不是每次调用 findMode 都会重新设置。

---

2. findMode 里的“再初始化”

def findMode(self, root):
    self.count = 0
    self.maxCount = 0
    self.pre = None
    self.result = []

这里相当于每次运行算法前，把状态清空。
为什么要这样？因为：

• 这个类的成员变量会随着上一次的遍历而改变。
• 如果你第二次调用 findMode（比如同一个对象想找另一个树的众数），就会遗留下上次的状态。
• 所以必须在 findMode 里手动把它们“重置”。

---

3. 举个例子

sol = Solution()

print(sol.findMode(tree1))  # 第一次调用
print(sol.findMode(tree2))  # 第二次调用

如果没有 findMode 里的那几行重置：

• 第一次调用会正确输出 tree1 的众数。
• 第二次调用时，self.pre 还是上一次的节点对象，self.maxCount 还是上一次的值 → 结果会被污染，算出来的就错了。

---

✅ 总结：

• __init__：对象创建时的一次性初始化。
• findMode 里的重置：保证每次运行算法都从干净状态开始。

---

迭代法

class Solution:
    def findMode(self, root):
        st = []
        cur = root
        pre = None
        maxCount = 0  # 最大频率
        count = 0  # 统计频率
        result = []

        while cur is not None or st:
            if cur is not None:  # 指针来访问节点，访问到最底层
                st.append(cur)  # 将访问的节点放进栈
                cur = cur.left  # 左
            else:
                cur = st.pop()
                if pre is None:  # 第一个节点
                    count = 1
                elif pre.val == cur.val:  # 与前一个节点数值相同
                    count += 1
                else:  # 与前一个节点数值不同
                    count = 1

                if count == maxCount:  # 如果和最大值相同，放进result中
                    result.append(cur.val)

                if count > maxCount:  # 如果计数大于最大值频率
                    maxCount = count  # 更新最大频率
                    result = [cur.val]  # 很关键的一步，不要忘记清空result，之前result里的元素都失效了

                pre = cur
                cur = cur.right  # 右

        return result

236. 二叉树的最近公共祖先

本题其实是比较难的，可以先看我的视频讲解

https://programmercarl.com/0236.二叉树的最近公共祖先.html
视频讲解：https://www.bilibili.com/video/BV1jd4y1B7E2

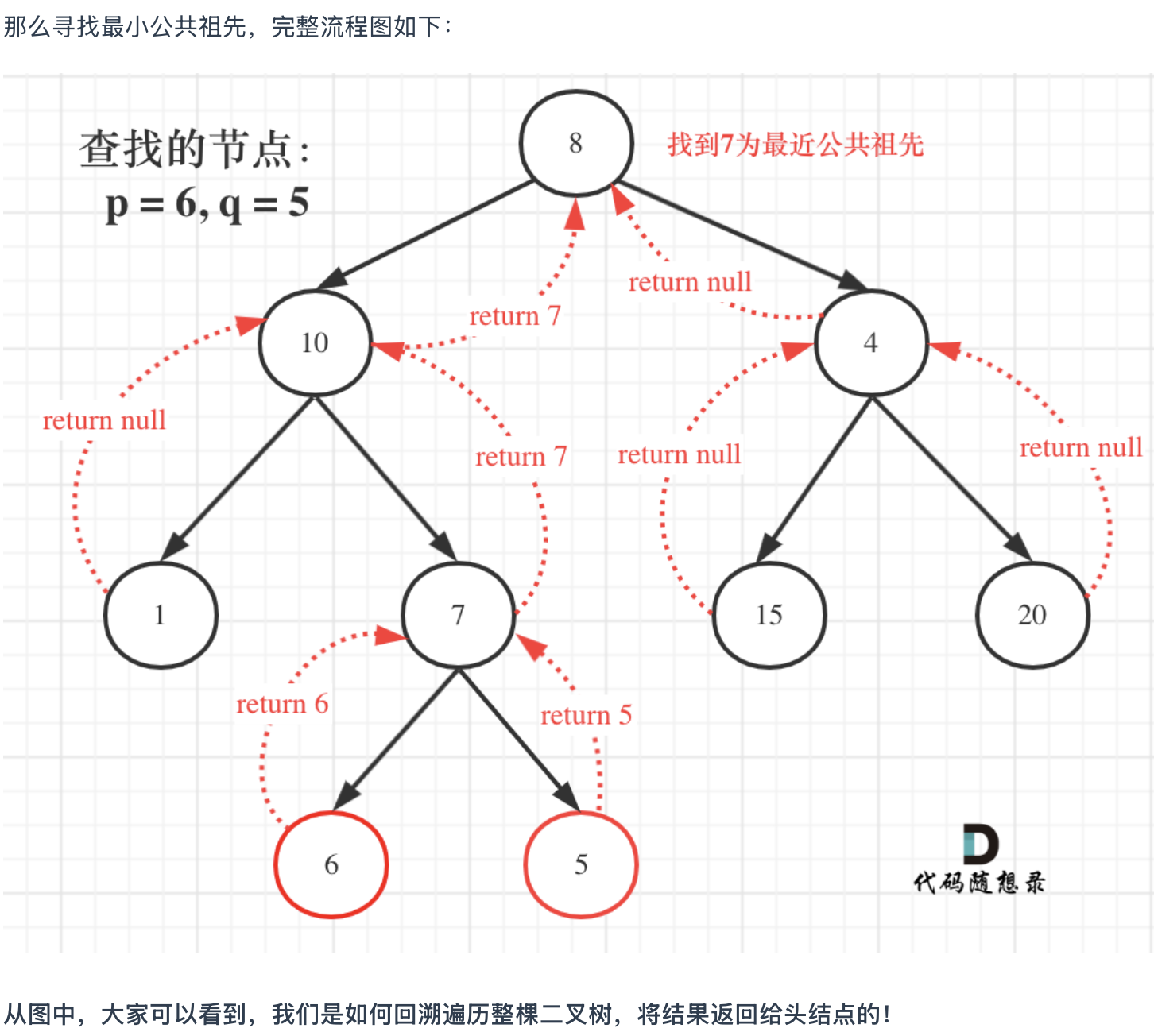
二叉树自底向下查找->回溯 二叉树回溯的过程就是从低到上

后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑

最简单情况：左子树出现p，右子树出现q，或者反过来。那么该节点就是最近公共祖先

思路：递归遍历，遇到p返回p,遇到q返回q，若左右子树返回值都不为空，那么中节点是最近公共祖先

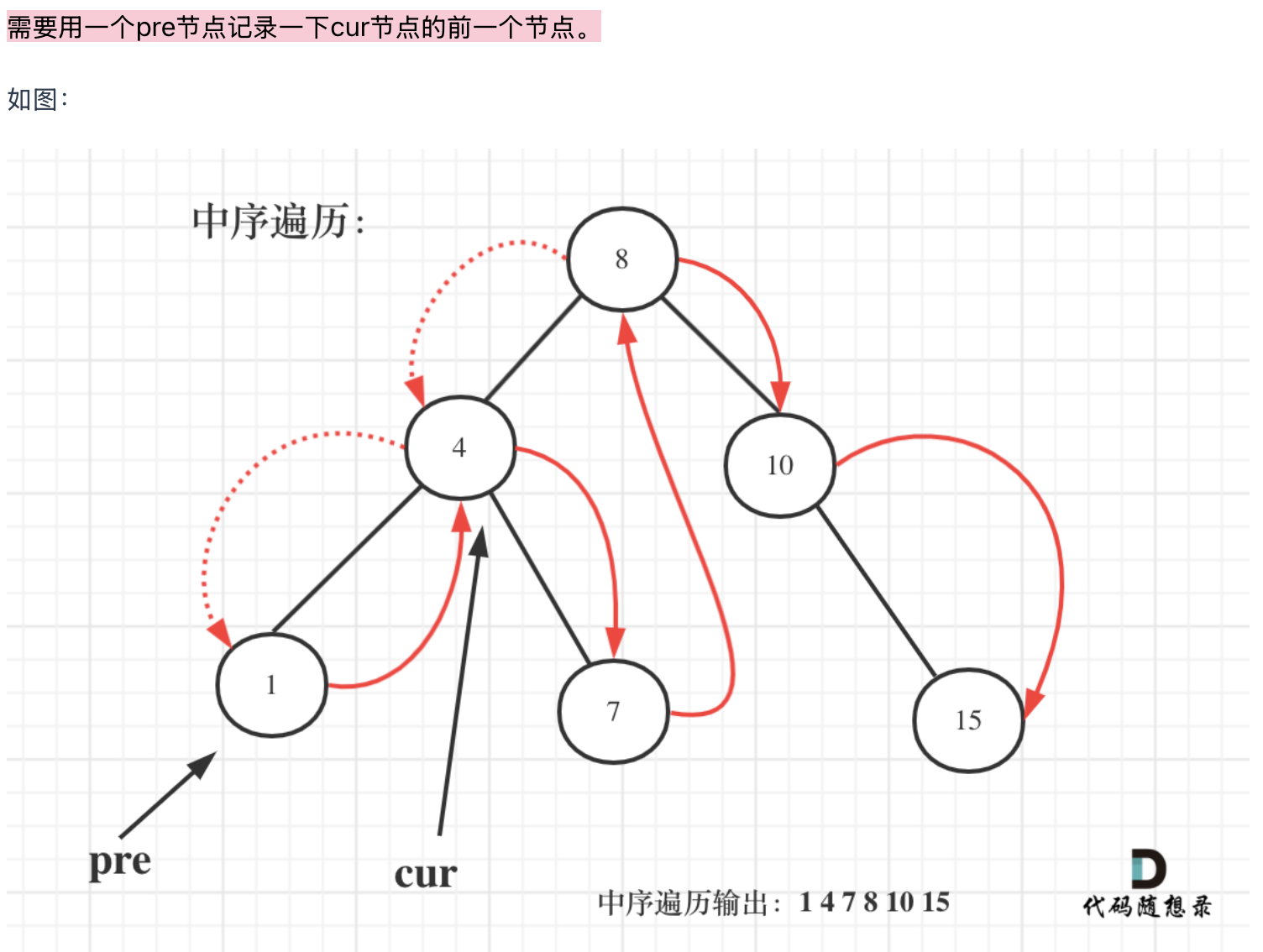
容易被忽略的情况：节点p/q本身就是要找的最近公共祖先

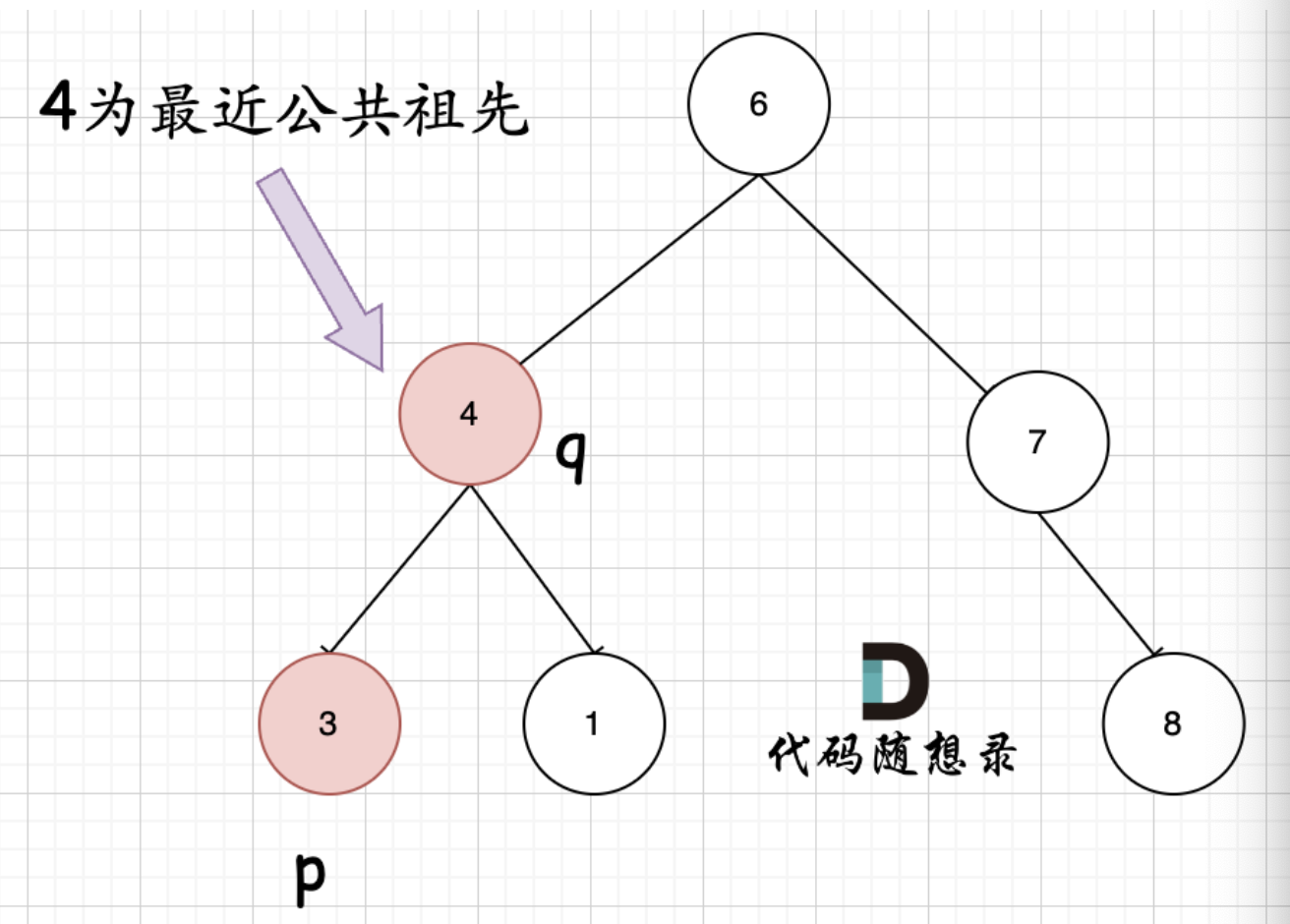
回忆递归三部曲

• 确定递归函数 返回值和参数

  本题中，确定是否找到了节点p/q--->返回值为bool类型

  但是还要返回公共节点--->需要返回treeNode *

  因此：

  遇到p/q，返回该节点。那么返回值不为空就代表找到了p/q

• 确定中止条件

  遇到空，则树空，返回空

  遇到p/q了，即节点本身是p/q，返回节点本身

  if root == p or root == q or root is None:
    return root
  

• 确定单层递归逻辑

  左右中，到中节点的时候需要对递归函数返回值座判断->函数有返回值

  

  

  

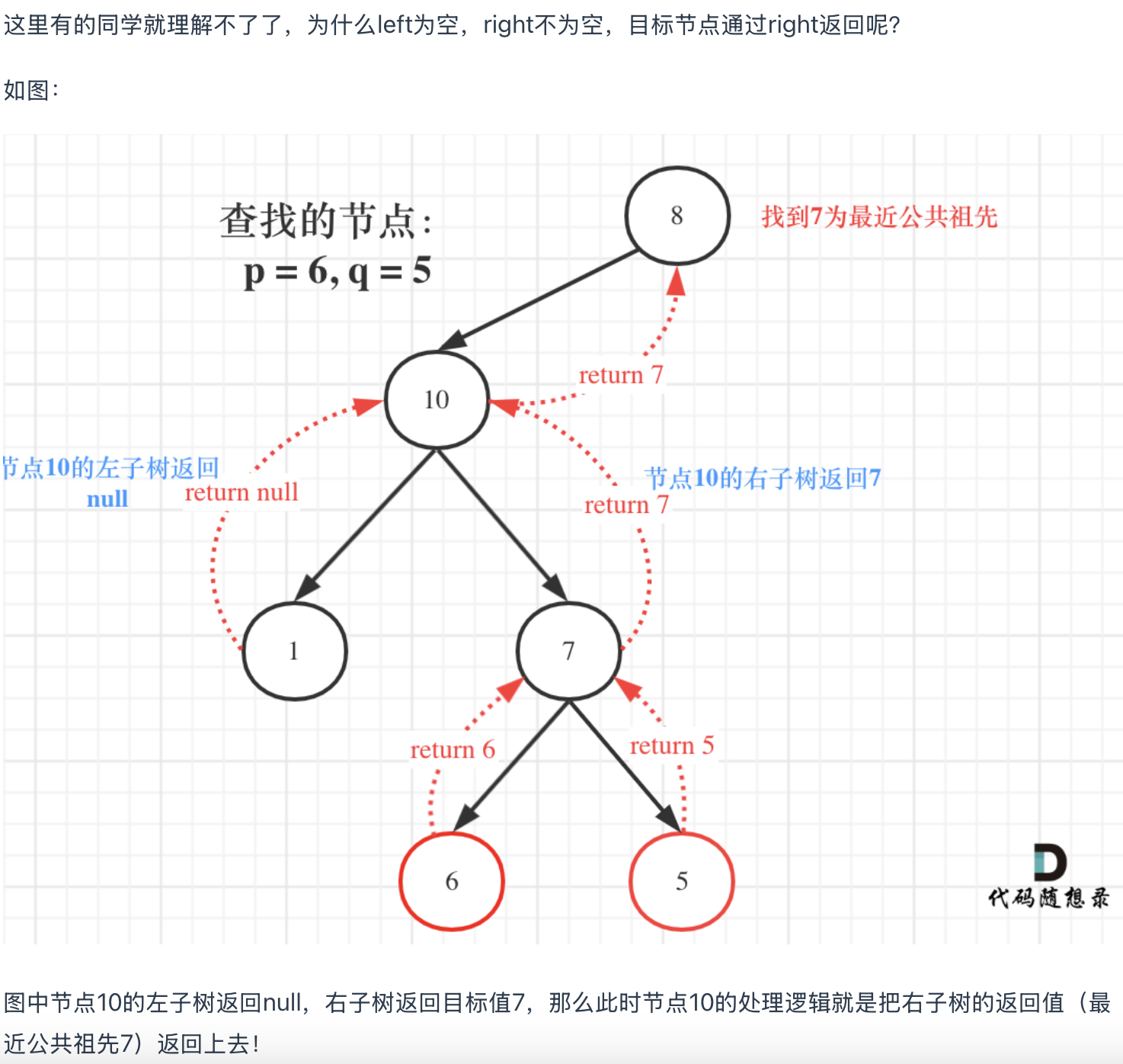
  若left和right都为空，那么返回left/right均可，就是返回空。

  

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        if root == q or root == p or root is None:
            return root

        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)

        if left is not None and right is not None:
            return root

        if left is None and right is not None:
            return right
        elif left is not None and right is None:
            return left
        else: 
            return None

精简版

class Solution:
  def lowestCommonAncestor(self, root, p, q):
      if root == q or root == p or root is None:
          return root

      left = self.lowestCommonAncestor(root.left, p, q)
      right = self.lowestCommonAncestor(root.right, p, q)

      if left is not None and right is not None:
          return root

      if left is None:
          return right
      return left