代码随想录算法训练营|Day 15
Day 15
第六章 二叉树part03
迭代法,大家可以直接过,二刷有精力的时候 再去掌握迭代法。
110.平衡二叉树 (优先掌握递归)
再一次涉及到,什么是高度,什么是深度,可以巩固一下。
题目链接/文章讲解/视频讲解:https://programmercarl.com/0110.平衡二叉树.html
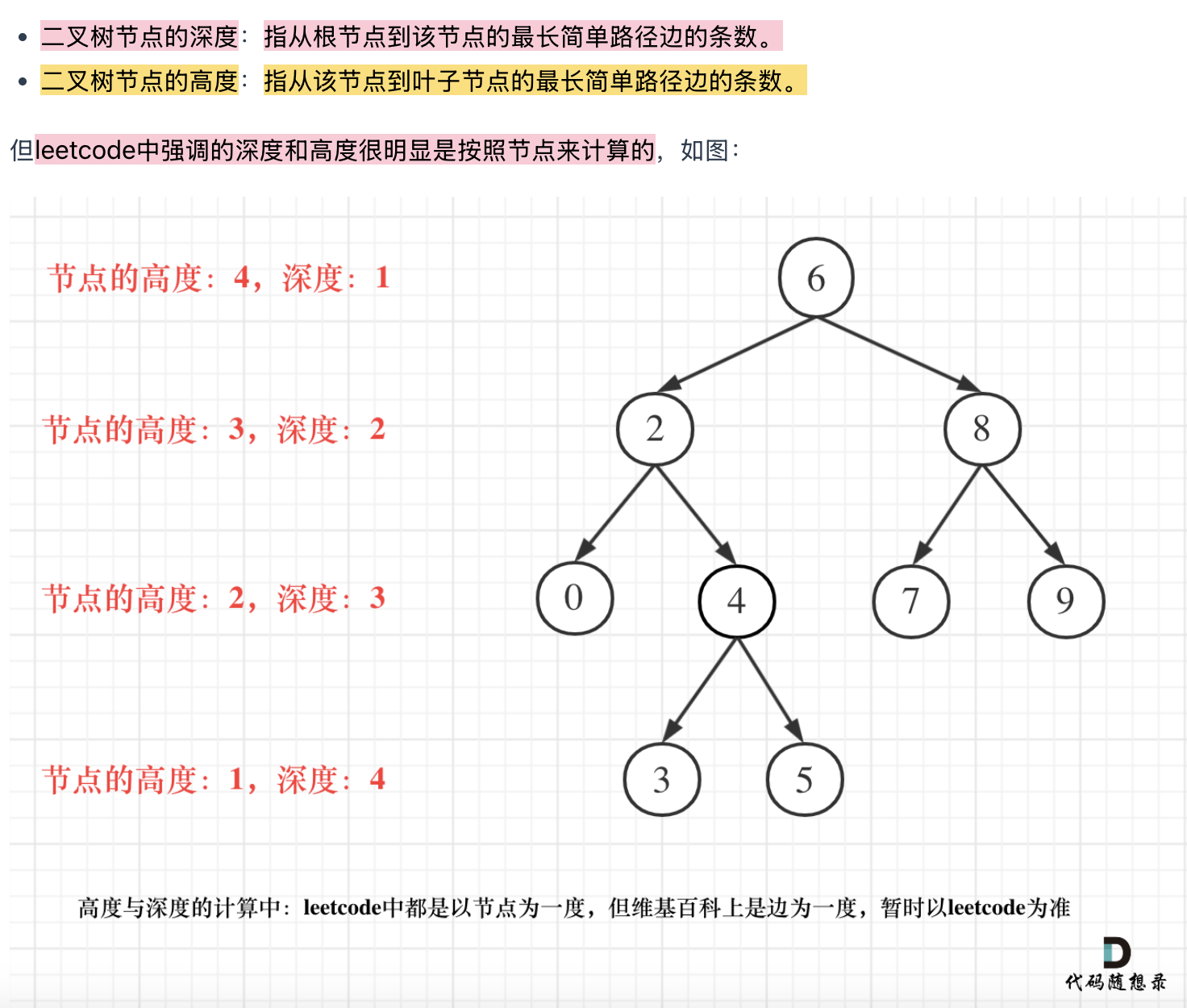
平衡二叉树的定义:该树所有节点的左右子树的高度相差不超过1
高度:距离叶子结点的距离。从下往上算,孩子的处理结果交给父节点 ->后序
深度:距离根结点的距离。从上往下,往下遍历一个就+1,不向上返回结果 ->前序
根结点的高度: 就是二叉树的最大深度
错误递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
def countHeight(node):
if not node:
return 0
return 1+ max(countHeight(node.left), countHeight(node.right))
return abs(countHeight(root.left)-countHeight(root.right)) <= 1
错误原因
你的实现只在根节点(root)处判断了左右子树高度差,却没有递归地去保证所有子节点也满足“平衡二叉树(balanced binary tree)”的定义:
对于每一个节点,其左子树高度(left subtree height)和右子树高度(right subtree height)之差都不能超过 1,且它的左右子树也都必须是平衡二叉树。
你的代码缺少对左右子树 isBalanced(root.left) 和 isBalanced(root.right) 的检查,只做了一次 countHeight 的比较,深层不平衡的子树就会漏掉。
另外,每次 countHeight 都是一次完整的子树遍历,导致最坏 O(n²) 的时间复杂度,在节点多时也容易超时(TLE)。
下面给出一个一趟递归(one‑pass traversal)就能同时计算高度(height)和判断平衡(balance)的写法:
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def dfs(node):
# 返回 node 的高度;若发现失衡则返回 -1 作为信号
if not node:
return 0
lh = dfs(node.left)
if lh == -1: # 左子树已经失衡
return -1
rh = dfs(node.right)
if rh == -1: # 右子树已经失衡
return -1
if abs(lh - rh) > 1: # 当前节点失衡
return -1
return max(lh, rh) + 1
return dfs(root) != -1
这样做能保证:
- 每个节点都检查了高度差 <= 1;
- 一旦发现任何子树失衡,就会向上“短路”(short‑circuit)返回 -1;
- 时间复杂度 O(n),只遍历一次。
正确递归
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
return self.get_hight(root) != -1
def get_hight(self, node):
if not node:
return 0
left = self.get_hight(node.left)
right = self.get_hight(node.right)
if left == -1 or right == -1 or abs(left - right) > 1:
return -1
return max(left, right) + 1
迭代法
class Solution:
def getDepth(self, cur):
st = []
if cur is not None:
st.append(cur)
depth = 0
result = 0
while st:
node = st[-1]
if node is not None:
st.pop()
st.append(node) # 中
st.append(None)
depth += 1
if node.right:
st.append(node.right) # 右
if node.left:
st.append(node.left) # 左
else:
node = st.pop()
st.pop()
depth -= 1
result = max(result, depth)
return result
def isBalanced(self, root):
st = []
if root is None:
return True
st.append(root)
while st:
node = st.pop() # 中
if abs(self.getDepth(node.left) - self.getDepth(node.right)) > 1:
return False
if node.right:
st.append(node.right) # 右(空节点不入栈)
if node.left:
st.append(node.left) # 左(空节点不入栈)
return True
这段代码用的是一种“显式栈(stack)+标记(marker)”的方法,来分别完成:
- 计算子树高度 的
getDepth(cur) - 遍历整棵树、对每个节点做高度差检查 的
isBalanced(root)
一、getDepth(cur) 如何工作
def getDepth(self, cur):
st = []
if cur is not None:
st.append(cur)
depth = 0
result = 0
while st:
node = st[-1]
if node is not None:
# ——“进入”这个节点 node
st.pop()
st.append(node) # 先把 node 重新压回去(用于后面回溯时匹配)
st.append(None) # 然后压一个 None 作标记
depth += 1 # 进入一层,深度 +1
# 按“先右后左”顺序入栈,确保下次循环中先处理左子树
if node.right:
st.append(node.right)
if node.left:
st.append(node.left)
else:
# ——“回溯”:碰到 None,就弹出标记和对应的节点,深度 -1
st.pop() # 弹出 None
st.pop() # 弹出上面对应的 node
depth -= 1
# 不断更新我们到过的最大深度
result = max(result, depth)
return result
-
st里同时存放TreeNode和None标记:- 栈顶是
TreeNode时,表示「还没进到它的左右子树」,我们就把它和一个None重新压回去,并depth += 1; - 栈顶是
None时,说明它对应的那个节点的左右子树都遍历完了,我们再把depth -= 1,相当于递归中的回溯。
- 栈顶是
-
depth始终记录当前栈顶路径的长度,result记录“遍历过程中见过的最大depth”,最终就是这棵子树的高度。
二、isBalanced(root) 如何利用它
def isBalanced(self, root):
st = []
if root is None:
return True
st.append(root)
while st:
node = st.pop()
# 对当前 node,分别算左右子树高度并比较
if abs(self.getDepth(node.left) - self.getDepth(node.right)) > 1:
return False
# 继续遍历左右子节点
if node.right:
st.append(node.right)
if node.left:
st.append(node.left)
return True
- 用一个栈做前序遍历:每碰到一个
node,都去算它左子树和右子树的高度差; - 只要有任何一个节点的高度差超过 1,就判为不平衡,提前返回
False; - 全部节点都检查完才返回
True。
三、优缺点
-
优点
- 代码逻辑非常直观:先写一个通用的“算高度”函数,再对每个节点“算左右高度差”。
- 不用递归函数调用栈,改成了手动维护的
st。
-
缺点
- 效率较低:每访问一个节点都要重新跑一遍
getDepth,最坏 O(n²)。 - 空间上,栈里可能最多存
O(h)个元素(h 是树高),跟递归栈差不多。
- 效率较低:每访问一个节点都要重新跑一遍
实际上,更高效的做法是一次 DFS里边“自底向上”同时算高度和判断平衡性(时间 O(n))。但这个解法对于中小规模的树也完全能通过,只是当节点很多时会比较慢。
depth 在这个算法里,其实就是模拟递归时“调用栈”的深度:
- “进入”(enter)节点时,我们相当于在递归里做了一个函数调用,它所在的那一层深度就要
depth += 1。 - “回溯”(leave)节点时,就相当于从那个递归调用里返回,你要把深度退回去,也就是
depth -= 1。
具体到代码流程:
- 当你第一次看到一个非
None的node,就把它和一个None标记一起压回栈,并做depth += 1,表示你“走”到它这一层了。 - 紧接着又把它的左右子节点(如果有)压进去,继续往更深层走。
- 直到子节点都处理完,你会再次遇到那个
None,这时弹出None以及它对应的node,就意味着“我已经把这个节点的左右子树都走完了”,要从这一层回到上一层,就要depth -= 1。
如果不做 depth -= 1,depth 就只会一直累加,从来不会减少,那得到的最大深度也就不对了。
简单说,每次“进一层”就 +1,每次“出一层”就 −1,才能正确追踪当前遍历路径的长度,最后 result = max(result, depth) 才是真正的树高。
下面我们用一棵小树来演示 getDepth 中 depth += 1 和 depth -= 1 的过程,假设树结构如下:
1
/ \
2 3
/
4
也就是:
- 根节点是 1
- 1 的左子节点是 2,右子节点是 3
- 2 的左子节点是 4
调用 getDepth(1) 时,栈和 depth、result 的变化(只列前几步)大致如下(栈顶在右侧):
| 步骤 | 栈 内容 | 操作 | depth | result |
|---|---|---|---|---|
| 初始化 | [1] |
depth=0,result=0 | 0 | 0 |
| 1 | [1] |
看到 1(非 None)→ pop→ push(1)、push(None),depth=1;再按 “右→左” 入栈 3,2 |
1 | max(0,1)=1 |
→ [1, None, 3, 2] |
||||
| 2 | [1, None, 3, 2] |
看到 2→ pop→ push(2)、push(None),depth=2;再按“右→左”入栈(2 无右,左是 4) |
2 | max(1,2)=2 |
→ [1, None, 3, 2, None, 4] |
||||
| 3 | [1, None, 3, 2, None, 4] |
看到 4→ pop→ push(4)、push(None),depth=3;(4 无子) |
3 | max(2,3)=3 |
→ [1, None, 3, 2, None, 4, None] |
||||
| 4 | ...None 在栈顶 |
看到 None→ pop(None)、pop(对应的 4),相当于“回溯”出 4,depth=2 |
2 | 3 |
| 5 | 接着又碰到上一个 None(对应 2) |
再次 pop 标记 和 2,depth=1 | 1 | 3 |
| … | … | 最后整个栈空了,返回 result=3 |
0 | 3 |
- 每次遇到节点(非
None),都相当于“递归进一层”,先depth += 1; - 每次遇到
None标记,都相当于“递归出一层”,再depth -= 1; result记录遍历过程中depth的最大值,最终就是这棵树的高度(本例中高度 = 3)。
这样,depth -= 1 就是为了在“子树遍历完毕、回到父节点”时,正确地把当前深度退回去。
迭代法精简版
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
height_map = {}
stack = [root]
while stack:
node = stack.pop()
if node:
stack.append(node) # 中
stack.append(None)
# 采用数组进行迭代,先将右节点加入,保证左节点能够先出栈
if node.right: # 右
stack.append(node.right)
if node.left: # 左
stack.append(node.left)
else:
real_node = stack.pop()
left, right = height_map.get(real_node.left, 0), height_map.get(real_node.right, 0)
if abs(left - right) > 1:
return False
height_map[real_node] = 1 + max(left, right)
return True
这个版本用的是 迭代的后序遍历 + 备忘(memoization) 来 自底向上 计算每个节点的高度并顺手检查平衡性。流程可以分两部分来看:
1. 数据结构
-
height_map: Dict[TreeNode, int]
存放每个节点处理完以后算出的高度:height_map[node] = 1 + max(height_map[left], height_map[right]) -
stack: List[TreeNode or None]
用来模拟递归调用栈,里面既放TreeNode,也放None作为“标记”(marker)。
2. 遍历逻辑
stack = [root]
while stack:
node = stack.pop()
if node: # 正常节点,等同于“递归进入”时的前序逻辑
stack.append(node) # —— 中
stack.append(None) # —— 标记:之后遇到它就知道要“后序”处理 node
if node.right: # —— 右
stack.append(node.right)
if node.left: # —— 左
stack.append(node.left)
else:
# 遇到 None,就进行“后序”操作:pop 出真实节点 real_node
real_node = stack.pop()
left_h = height_map.get(real_node.left, 0)
right_h = height_map.get(real_node.right, 0)
# 平衡性检查
if abs(left_h - right_h) > 1:
return False
# 记录 real_node 的高度
height_map[real_node] = 1 + max(left_h, right_h)
-
遇到一个
TreeNode:- 先把它再压回去(
stack.append(node)) - 压一个
None标记,表示“它的子树出栈完以后要回来处理它” - 再按「先右后左」的顺序把左右子节点压进来,这样出栈时就能先遍历左子树、再右子树
- 先把它再压回去(
-
遇到一个
None:- 说明对应的
TreeNode的左右子树都已经“后序”遍历完了, - 这时
stack.pop()再拿回那个TreeNode(我们叫它real_node), - 就可以从
height_map里拿到它左右子树的高度,先做abs(left_h - right_h) ≤ 1的平衡性校验, - 校验过后,把
real_node的高度算出来1 + max(left_h, right_h)存到height_map。
- 说明对应的
3. 优劣对比
-
优点
- 一次遍历 就完成:既算高度又判平衡,时间 O(n)。
- 不会有重复的
getDepth调用,也不用递归,适合节点多时避免递归深度问题。
-
缺点
- 需要额外的
height_map存储每个节点的高度,空间 O(n)。 - 代码稍微复杂一些,要理解「None 标记」和「先右后左」的入栈顺序。
- 需要额外的
总的来说,这是把“递归后序遍历+备忘”改写成了显式栈迭代的版本,效率和递归版一样都是 O(n),但避免了函数调用开销,也很利于定制化控制遍历顺序。
257. 二叉树的所有路径 (优先掌握递归)
这是大家第一次接触到回溯的过程, 我在视频里重点讲解了 本题为什么要有回溯,已经回溯的过程。
如果对回溯 似懂非懂,没关系, 可以先有个印象。
题目链接/文章讲解/视频讲解:https://programmercarl.com/0257.二叉树的所有路径.html
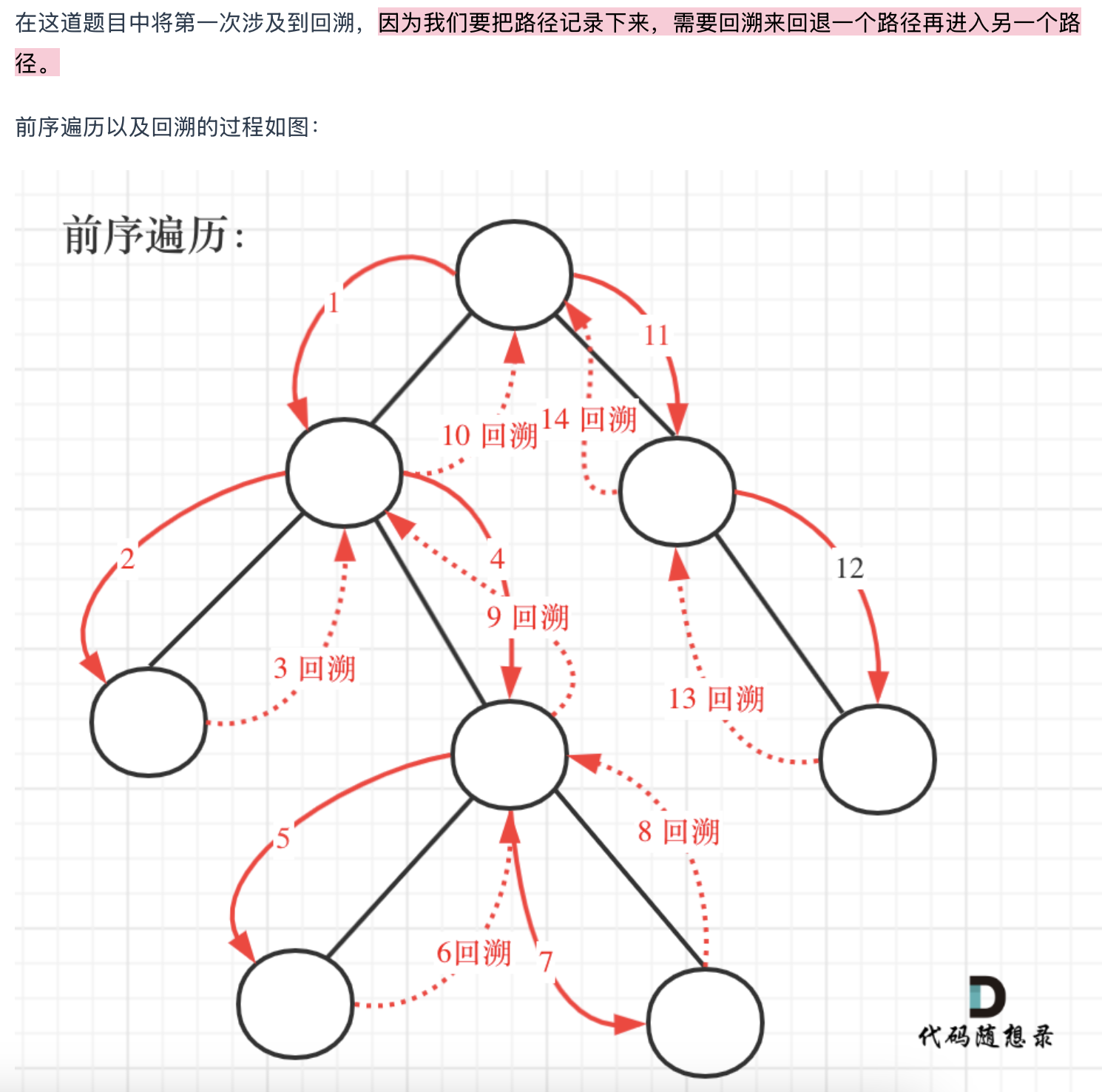
递归 到路径终点收割
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
#确定是前序
#中左右
if not root:
return []
res = []
def dfs(node, res, path):
if not node.left and not node.right:
res.append(path)
if node.left:
dfs(node.left, res, path+"->"+str(node.left.val))
if node.right:
dfs(node.right, res, path+"->"+str(node.right.val))
dfs(root, res, str(root.val))
return res
回溯和递归相辅相成,只要有递归就一定有回溯
迭代法
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
# 题目中节点数至少为1
stack, path_st, result = [root], [str(root.val)], []
while stack:
cur = stack.pop()
path = path_st.pop()
# 如果当前节点为叶子节点,添加路径到结果中
if not (cur.left or cur.right):
result.append(path)
if cur.right:
stack.append(cur.right)
path_st.append(path + '->' + str(cur.right.val))
if cur.left:
stack.append(cur.left)
path_st.append(path + '->' + str(cur.left.val))
return result
这个解法用的是 显式栈(stack)+ 同步路径栈(path_st) 来做一次深度优先搜索(DFS),在遍历时 边走边拼接 从根到当前节点的字符串,遇到叶子节点就把整条路径存到结果里。具体流程如下:
-
初始化
stack = [root] # 存节点 path_st = [str(root.val)] # 存对应节点的“到这里为止”的路径字符串 result = [] # 最终结果stack[i]↔path_st[i]保持一一对应。
-
循环遍历
while stack: cur = stack.pop() path = path_st.pop() ...每次从栈顶取出一个节点
cur,以及它对应的路径path。 -
遇到叶子节点
if not (cur.left or cur.right): result.append(path)如果
cur既没有左子树也没有右子树,就把当前完整的path(形如"1->2->5")加入result。 -
压入子节点,继续“走深”
为保证「先左子树后右子树」的顺序(虽然结果顺序通常不强制,但这也是典型写法),我们先把右子节点压栈,再把左子节点压栈:if cur.right: stack.append(cur.right) path_st.append(path + '->' + str(cur.right.val)) if cur.left: stack.append(cur.left) path_st.append(path + '->' + str(cur.left.val))- 对于每个子节点,都在原来的
path后面加上"->子节点值",保证path_st一直记录“从根到这个子节点”的完整路径。
- 对于每个子节点,都在原来的
-
结束
当stack为空,表示所有从根出发的路径都被探索过,result就包含了所有根到叶子的路径。
举例演示
以这棵树为例:
1
/ \
2 3
\
5
-
初始
stack = [1] path_st = ["1"] result = [] -
弹出 1
cur = 1, path = "1" 1 不是叶子,压: 右节点 3 → stack.append(3), path_st.append("1->3") 左节点 2 → stack.append(2), path_st.append("1->2") stack = [3, 2] path_st = ["1->3", "1->2"] -
弹出 2
cur = 2, path = "1->2" 2 不是叶子,只有右子 5,压: 右节点 5 → stack.append(5), path_st.append("1->2->5") stack = [3, 5] path_st = ["1->3", "1->2->5"] -
弹出 5
cur = 5, path = "1->2->5" 5 是叶子 → result.append("1->2->5") stack = [3] path_st = ["1->3"] result = ["1->2->5"] -
弹出 3
cur = 3, path = "1->3" 3 是叶子 → result.append("1->3") stack = [] path_st = [] result = ["1->2->5", "1->3"]
结束,返回 ["1->2->5", "1->3"]。
复杂度
- 时间:O(n·h)
每个节点进出栈一次,拼接字符串需要 O(h)(h 是树高),最坏退化为 O(n²); - 空间:O(n·h)
栈和路径栈各占 O(n),每条路径字符串占 O(h);
这个迭代写法和递归版的思路完全等价,优点是不依赖系统递归栈,方便掌控遍历顺序。
递归法+回溯
# Definition for a binary tree node.
class Solution:
def traversal(self, cur, path, result):
path.append(cur.val) # 中
if not cur.left and not cur.right: # 到达叶子节点
sPath = '->'.join(map(str, path))
result.append(sPath)
return
if cur.left: # 左
self.traversal(cur.left, path, result)
path.pop() # 回溯
if cur.right: # 右
self.traversal(cur.right, path, result)
path.pop() # 回溯
def binaryTreePaths(self, root):
result = []
path = []
if not root:
return result
self.traversal(root, path, result)
return result
这种写法是典型的「递归 DFS + 回溯」——用一条可变的 path 列表自顶向下维护当前遍历到的节点值,遇到叶子就把它拼成一条完整路径,回退时再把多加的节点去掉。具体流程:
-
进入节点(pre‑order “中”)
path.append(cur.val)把当前节点值加到
path末尾。 -
到达叶子
if not cur.left and not cur.right: sPath = '->'.join(map(str, path)) result.append(sPath) return如果左右子都空,就把
path用"->"拼成字符串,存到result,然后直接return不再深入。 -
递归左子树(“左”)
if cur.left: self.traversal(cur.left, path, result) path.pop() # 回溯:把刚才加的 cur.left.val 移除 -
递归右子树(“右”)
if cur.right: self.traversal(cur.right, path, result) path.pop() # 回溯:把刚才加的 cur.right.val 移除 -
初始调用
在binaryTreePaths里先判断空树,然后self.traversal(root, [], result)最终
result就包含了所有从根到叶子的路径字符串。
关键点
path里始终保存「从根走到当前节点」的值序列。- 每次深入一个子节点,就
append;回退到父节点时,就pop,保证下一条分支的path正确。 - 时间复杂度 O(n·h),其中 h 是树高(因为每到叶子要做一次 join);空间复杂度 O(h) 用于递归栈和
path列表。
我的递归法不体现回溯的原因:
这段代码也是典型的“递归 DFS”(深度优先搜索)+“前序遍历”(pre‑order: 中→左→右)来 边走边拼接 根到当前节点的路径字符串,一旦到叶子节点就把这条路径加入结果集。和你之前看到的「可变列表+显式回溯」不同,这里利用了 Python 字符串不可变(immutable) 的特性:每次 path + '->'+… 都会返回一个全新的字符串,不会污染父分支的 path,所以根本不需要手动 pop() 回溯。
一、代码结构和流程
def binaryTreePaths(self, root):
if not root:
return []
res = []
# dfs(node, res, path):
# node: 当前节点
# path: 到 node 为止的整条路径字符串
def dfs(node, res, path):
# 1. 如果是叶子节点,直接把 path 加入 res
if not node.left and not node.right:
res.append(path)
# 2. 前序“中”已经做了,就是 path 参数
# 下面先“左”、再“右”
if node.left:
# 注意:path+"->"+… 产生新字符串,不影响原来的 path
dfs(node.left, res, path + "->" + str(node.left.val))
if node.right:
dfs(node.right, res, path + "->" + str(node.right.val))
# 从根开始,初始路径就是根节点值本身
dfs(root, res, str(root.val))
return res
-
先序含义(中→左→右)
- “中” 是把当前
path当成已经到达node的路径; - 然后依次递归左子树和右子树。
- “中” 是把当前
-
叶子检测
if not node.left and not node.right: res.append(path)只在真正到叶子(leaf)时,才把当前完整路径写入
res。 -
字符串不可变——无需回溯
每次调用dfs(child, res, path + "->" + str(child.val))path + "->"+…都会返回一个 新 的字符串实例,父调用里的path保持不变。
这样,不同分支互不干扰,也不用像操作列表那样在递归返回后再pop()。
二、演示一个简单例子
1
/ \
2 3
\
5
-
dfs(1, [], "1")1不是叶子- 先左:
dfs(2, [], "1->2")
-
dfs(2, [], "1->2")2不是叶子(有右子)- 左子不存在,跳过
- 右子:
dfs(5, [], "1->2->5")
-
dfs(5, [], "1->2->5")5是叶子 →res.append("1->2->5")- 返回上层
-
回到
dfs(1, ["1->2->5"], "1"),接着处理右子:dfs(3, ["1->2->5"], "1->3")
-
dfs(3, ["1->2->5"], "1->3")3是叶子 →res.append("1->3")
最终 res = ["1->2->5", "1->3"],正是所有从根到叶子的路径。
三、复杂度
-
时间复杂度 O(n·h):
- n 个节点,每个节点做一次字符串拼接,拼接花费 O(h)(h 是树高)。
-
空间复杂度 O(h):
- 递归栈最深 h 层;每层维护一个长度 O(h) 的
path临时字符串。
- 递归栈最深 h 层;每层维护一个长度 O(h) 的
这种写法既清晰又不易出错,适合大多数二叉树「根到叶子路径」题目。
404.左叶子之和 (优先掌握递归)
其实本题有点文字游戏,搞清楚什么是左叶子,剩下的就是二叉树的基本操作。
题目链接/文章讲解/视频讲解:https://programmercarl.com/0404.左叶子之和.html
注意:只有当前遍历的节点是父节点,才能判断其子节点是不是左叶子

递归 后序
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root):
if root is None:
return 0
if root.left is None and root.right is None:
return 0
leftValue = self.sumOfLeftLeaves(root.left) # 左
if root.left and not root.left.left and not root.left.right: # 左子树是左叶子的情况
leftValue = root.left.val
rightValue = self.sumOfLeftLeaves(root.right) # 右
sum_val = leftValue + rightValue # 中
return sum_val
递归 后序 精简版
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root):
if root is None:
return 0
leftValue = 0
if root.left is not None and root.left.left is None and root.left.right is None:
leftValue = root.left.val
return leftValue + self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)
迭代法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root):
if root is None:
return 0
st = [root]
result = 0
while st:
node = st.pop()
if node.left and node.left.left is None and node.left.right is None:
result += node.left.val
if node.right:
st.append(node.right)
if node.left:
st.append(node.left)
return result
222.完全二叉树的节点个数(优先掌握递归)
需要了解,普通二叉树 怎么求,完全二叉树又怎么求
题目链接/文章讲解/视频讲解:https://programmercarl.com/0222.完全二叉树的节点个数.html
普适的递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
return 1 + self.countNodes(root.left) + self.countNodes(root.right)
这种属于后序的写法,因为左右节点的信息收集完后返回上一层的父节点
我的理解:若是后序,信息需要返回父节点,那么递归的时候需要return somthing,
而从上开始往下遍历,像是前序那样子,就是到空节点以后直接return,有额外的变量,如
max_depth或result这种变量去记录和更新遍历过程中的信息
也可以用层序遍历
import collections
class Solution:
def countNodes(self, root: TreeNode) -> int:
queue = collections.deque()
if root:
queue.append(root)
result = 0
while queue:
size = len(queue)
for i in range(size):
node = queue.popleft()
result += 1 #记录节点数量
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result
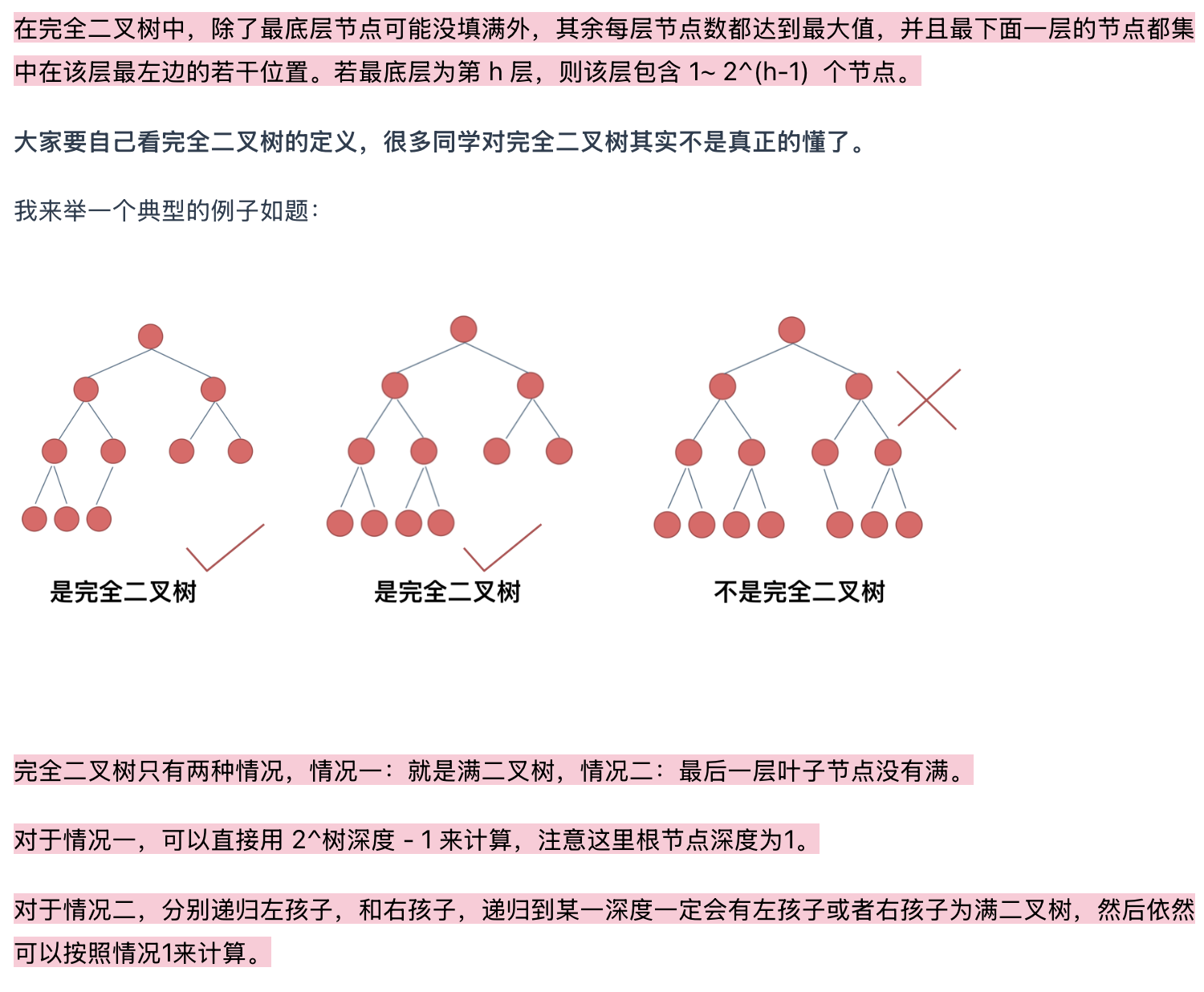
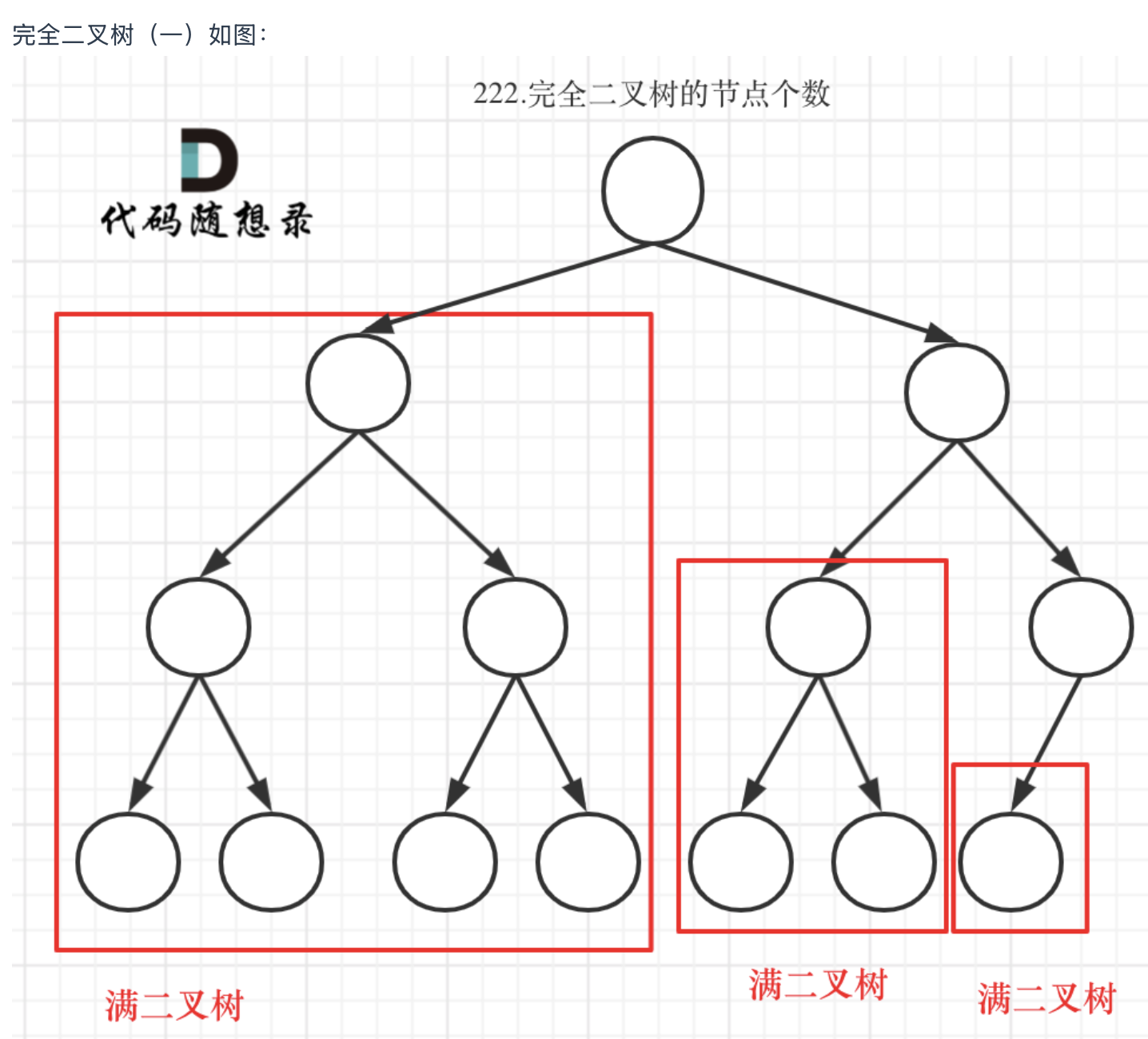
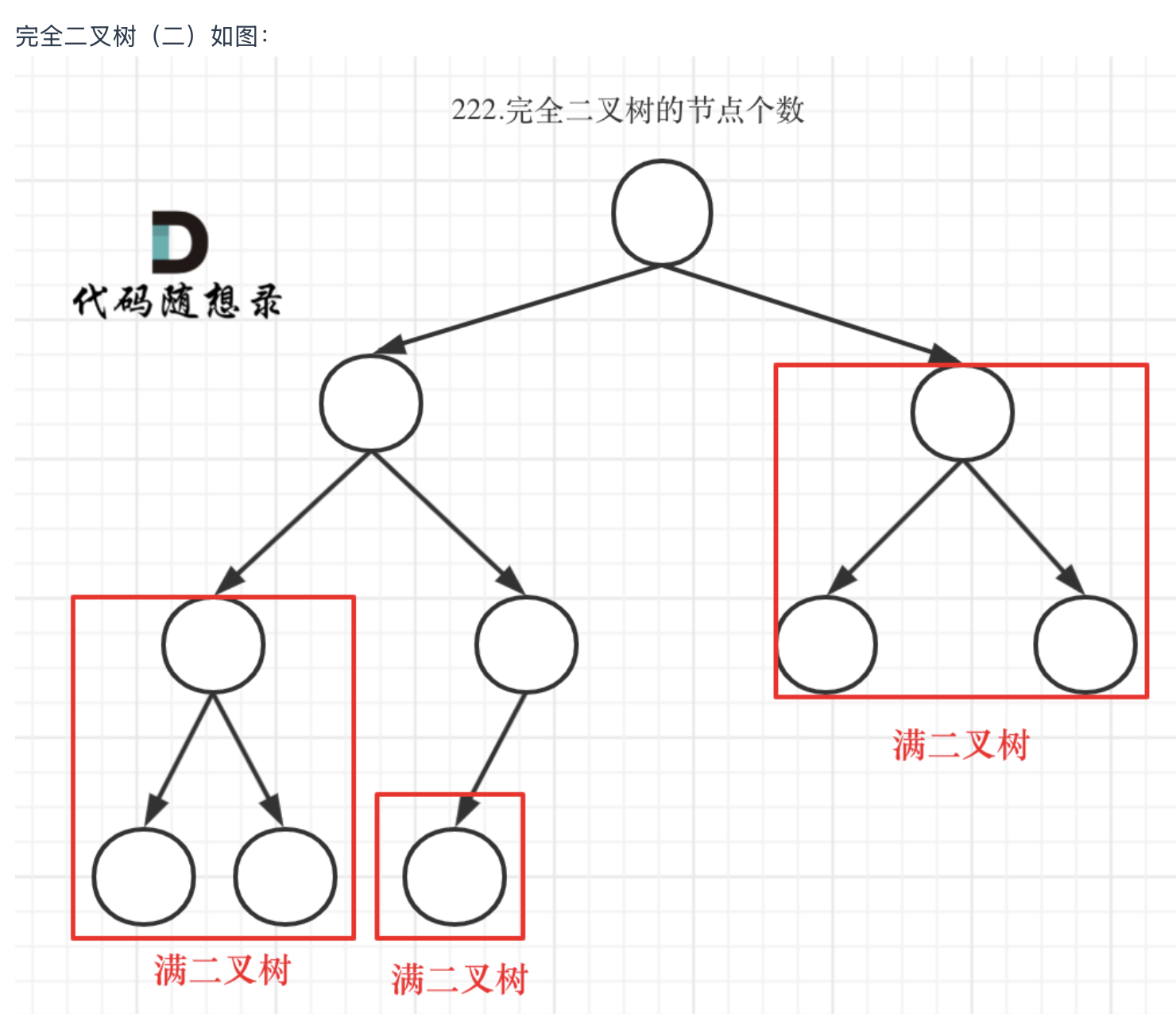
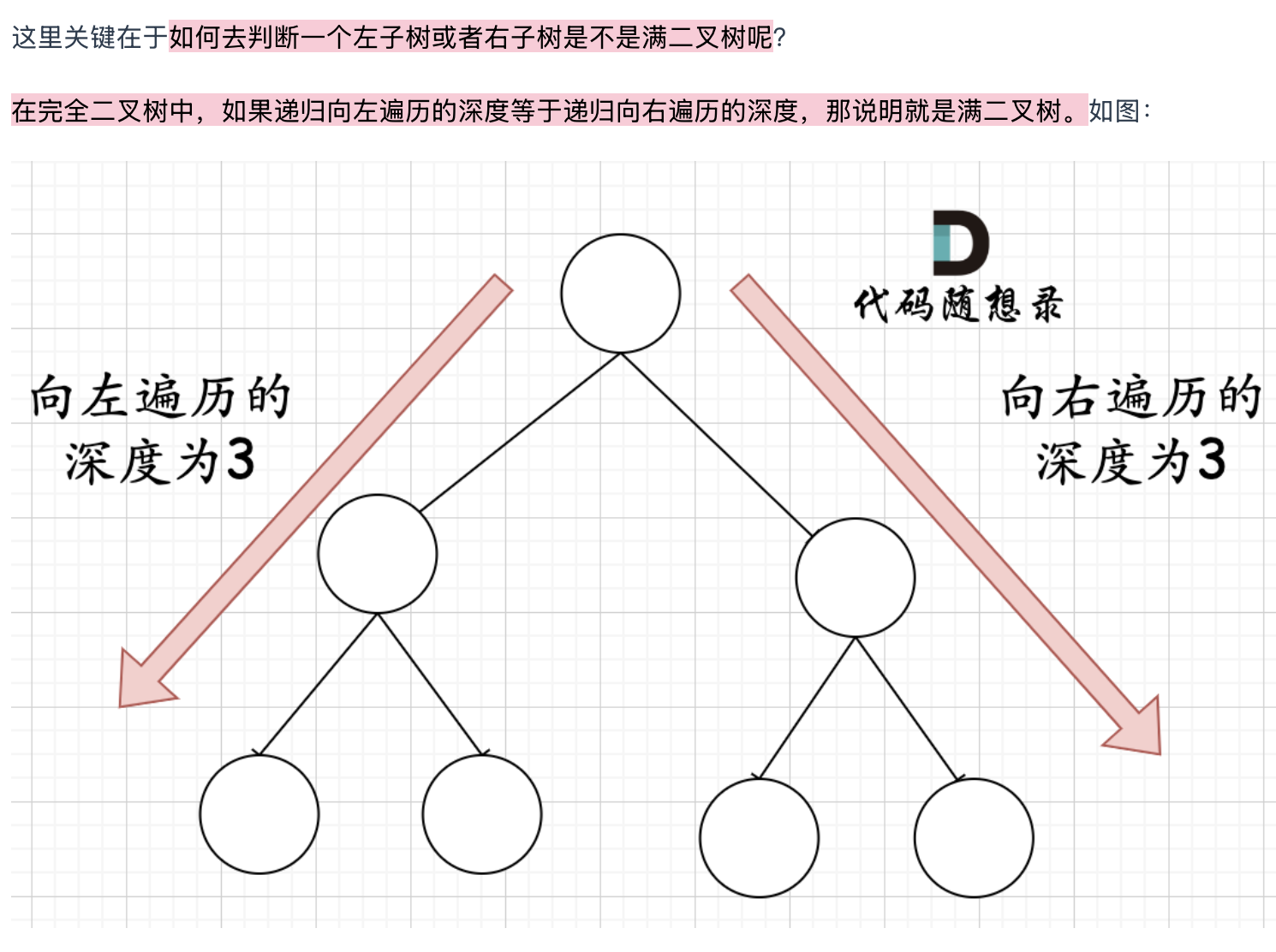
利用完全二叉树的特性
写法一
class Solution:
def countNodes(self, root: TreeNode) -> int:
if not root:
return 0
left = root.left
right = root.right
leftDepth = 0 #这里初始为0是有目的的,为了下面求指数方便
rightDepth = 0
while left: #求左子树深度
left = left.left
leftDepth += 1
while right: #求右子树深度
right = right.right
rightDepth += 1
if leftDepth == rightDepth:
return (2 << leftDepth) - 1 #注意(2<<1) 相当于2^2,所以leftDepth初始为0
return self.countNodes(root.left) + self.countNodes(root.right) + 1
leftDepth+1才是深度
满二叉树节点个数计算公式: 2^树深度-1
在 Python 里,<< 是按位(bitwise)左移运算符。
- 表达式
x << y的含义是把整数x的二进制向左移动y位,空出来的低位补 0。 - 从算术意义上看,这相当于
x * (2**y)。
所以
2 << leftDepth
等价于
2 * (2**leftDepth)
# 也就是 2**(leftDepth + 1)
举几个例子帮助理解:
leftDepth = 0
2 << 0 # = 2 * (2**0) = 2 * 1 = 2 (也即 2**1)
leftDepth = 1
2 << 1 # = 2 * (2**1) = 2 * 2 = 4 (也即 2**2)
leftDepth = 2
2 << 2 # = 2 * (2**2) = 2 * 4 = 8 (也即 2**3)
在你的代码里写的是
(2 << leftDepth) - 1
就相当于
2**(leftDepth + 1) - 1
这正好是节点全满的完美二叉树在高度为 leftDepth+1 时的节点总数。
写法二
class Solution: # 利用完全二叉树特性
def countNodes(self, root: TreeNode) -> int:
if not root: return 0
count = 1
left = root.left; right = root.right
while left and right:
count+=1
left = left.left; right = right.right
if not left and not right: # 如果同时到底说明是满二叉树,反之则不是
return 2**count-1
return 1+self.countNodes(root.left)+self.countNodes(root.right)
写法三
class Solution: # 利用完全二叉树特性
def countNodes(self, root: TreeNode) -> int:
if not root: return 0
count = 0
left = root.left; right = root.right
while left and right:
count+=1
left = left.left; right = right.right
if not left and not right: # 如果同时到底说明是满二叉树,反之则不是
return (2<<count)-1
return 1+self.countNodes(root.left)+self.countNodes(root.right)
写法二三的区别:count从1还是0开始
从1开始,最后count为树深度
从0开始,count+1才是树的深度
2<<count,代表2向左移动两位,相当于2^(count+1)





 浙公网安备 33010602011771号
浙公网安备 33010602011771号