代码随想录算法训练营|Day 14

Day 14

第六章 二叉树 part02

226.翻转二叉树 （优先掌握递归）

这道题目 一些做过的同学 理解的也不够深入，建议大家先看我的视频讲解，无论做过没做过，都会有很大收获。

题目链接/文章讲解/视频讲解：https://programmercarl.com/0226.翻转二叉树.html

用前序和后序遍历最合适

递归三部曲
1.确定递归函数的参数和返回值
2.确定终止条件
3.确定单层递归的逻辑 ->二叉树中，如何向下一层去遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root:
            return root
        
        def flipTree(node):
            if not node:
                return
            flipTree(node.left)
            flipTree(node.right)
            node.left, node.right = node.right, node.left
            
        flipTree(root)
        return root

递归前序遍历

中->左->右

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        root.left, root.right = root.right, root.left
        self.invertTree(root.left)
        self.invertTree(root.right)
        return root

迭代前序遍历

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None      
        stack = [root]        
        while stack:
            node = stack.pop()   
            node.left, node.right = node.right, node.left                   
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        return root

递归中序遍历

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        self.invertTree(root.left)
        root.left, root.right = root.right, root.left
        self.invertTree(root.left)
        return root

递归后序遍历

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        self.invertTree(root.left)
        self.invertTree(root.right)
        root.left, root.right = root.right, root.left
        return root

层序遍历

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        self.invertTree(root.left)
        self.invertTree(root.right)
        root.left, root.right = root.right, root.left
        return root

101. 对称二叉树 （优先掌握递归）

先看视频讲解，会更容易一些。

题目链接/文章讲解/视频讲解：https://programmercarl.com/0101.对称二叉树.html

判断是否是对称二叉树实质：根结点的左子树和右子树是否可以相互翻转
比较：左节点左孩子 vs 右节点右孩子 + 左节点右孩子 vs 右节点左孩子

二叉树最终是要考察如何遍历
这道题只能是后序
后序是左右中
因为要不断收集左右孩子的信息返回给上一层

递归法

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        return self.compare(root.left, root.right)
        
    def compare(self, left, right):
        #首先排除空节点的情况
        if left == None and right != None: return False
        elif left != None and right == None: return False
        elif left == None and right == None: return True
        #排除了空节点，再排除数值不相同的情况
        elif left.val != right.val: return False
        
        #此时就是：左右节点都不为空，且数值相同的情况
        #此时才做递归，做下一层的判断
        outside = self.compare(left.left, right.right) 
        #左子树：左、 右子树：右
        inside = self.compare(left.right, right.left) 
        #左子树：右、 右子树：左
        isSame = outside and inside #左子树：中、 右子树：中 （逻辑处理）
        return isSame

迭代法：使用队列

import collections
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        queue = collections.deque()
        queue.append(root.left) #将左子树头结点加入队列
        queue.append(root.right) #将右子树头结点加入队列
        while queue: #接下来就要判断这这两个树是否相互翻转
            leftNode = queue.popleft()
            rightNode = queue.popleft()
            if not leftNode and not rightNode: #左节点为空、右节点为空，此时说明是对称的
                continue
            
            #左右一个节点不为空，或者都不为空但数值不相同，返回false
            if not leftNode or not rightNode or leftNode.val != rightNode.val:
                return False
            queue.append(leftNode.left) #加入左节点左孩子
            queue.append(rightNode.right) #加入右节点右孩子
            queue.append(leftNode.right) #加入左节点右孩子
            queue.append(rightNode.left) #加入右节点左孩子
        return True

迭代法：使用栈

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        st = [] #这里改成了栈
        st.append(root.left)
        st.append(root.right)
        while st:
            rightNode = st.pop()
            leftNode = st.pop()
            if not leftNode and not rightNode:
                continue
            if not leftNode or not rightNode or leftNode.val != rightNode.val:
                return False
            st.append(leftNode.left)
            st.append(rightNode.right)
            st.append(leftNode.right)
            st.append(rightNode.left)
        return True

之所以既可以使用queue，又可以使用栈，是因为无论用queue还是栈，这个问题涉及的比较都是每次弹出两个的，成对比较

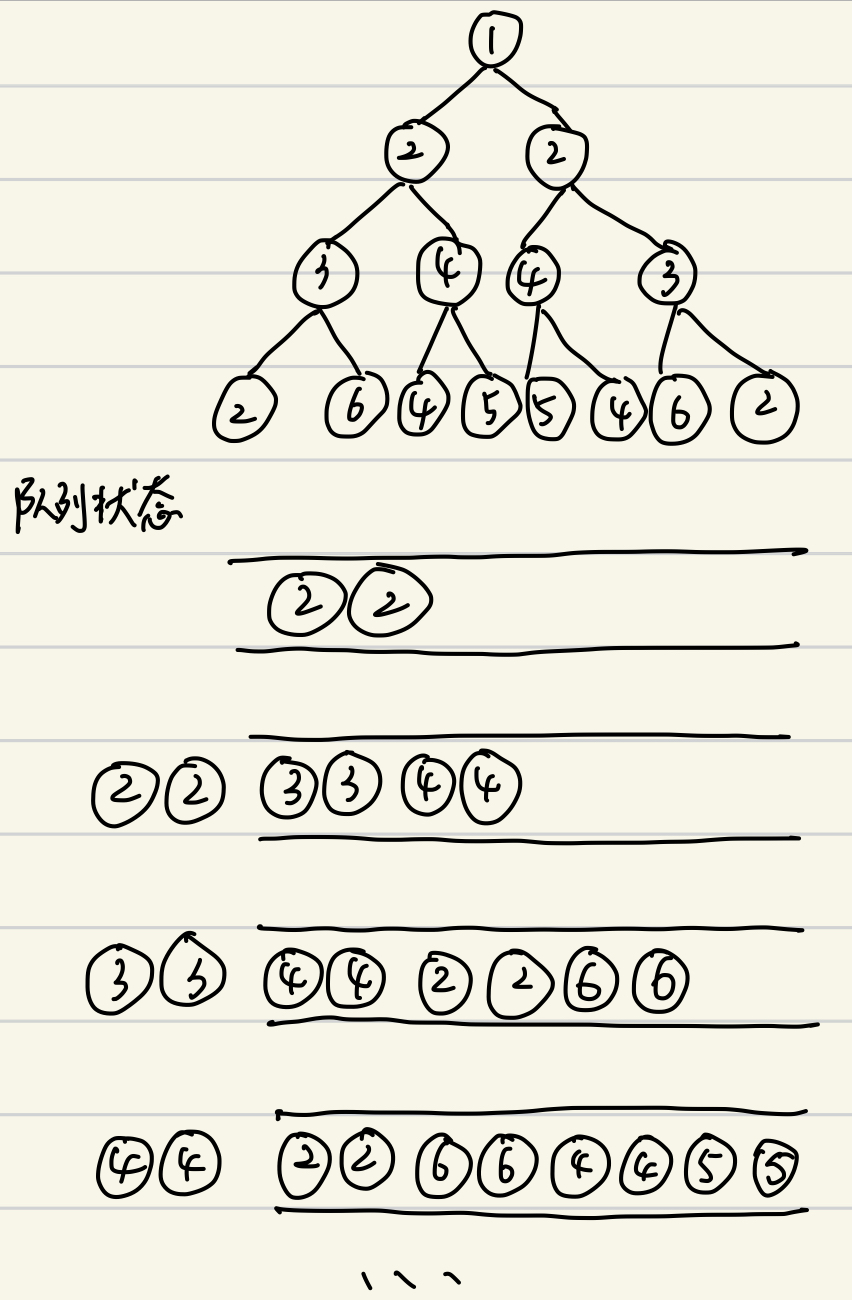
层序遍历

if not root:
            return True
        
        queue = collections.deque([root.left, root.right])
        
        while queue:
            level_size = len(queue)
            
            if level_size % 2 != 0:
                return False
            
            level_vals = []
            for i in range(level_size):
                node = queue.popleft()
                if node:
                    level_vals.append(node.val)
                    queue.append(node.left)
                    queue.append(node.right)
                else:
                    #注意这里是在收集每层node的时候加入None
                    #脑抽写成在queue中加入None就超时了我还
                    #看半天没看出来哪错了
                    level_vals.append(None)
                    
            if level_vals != level_vals[::-1]:
                return False
            
        return True

104.二叉树的最大深度 （优先掌握递归）

什么是深度，什么是高度，如何求深度，如何求高度，这里有关系到二叉树的遍历方式。

大家 要先看视频讲解，就知道以上我说的内容了，很多录友刷过这道题，但理解的还不够。

题目链接/文章讲解/视频讲解： https://programmercarl.com/0104.二叉树的最大深度.html

高度：从下往上计数 要把孩子的处理结果交给上层父节点
深度：从上往下计数 往下遍历一个就➕1 前序
求高度应该用 后序遍历 左右中
求深度应该用 前序遍历 中左右

根结点的高度 就是 二叉树的最大深度

递归法 后序

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        left_depth = self.maxDepth(root.left)
        right_depth = self.maxDepth(root.right)
        return 1 + max(left_depth, right_depth)

递归法 前序

class solution:
    def maxDepth(self,root:Optional[TreeNode]) -> int:
        max_d = 0

        def dfs(node, depth):
            nonlocal max_d
            if not node:
                max_d = max(max_d, depth)
                return
            dfs(node.left, depth+1)
            dfs(node.right, depth+1)

        dfs(root, 0)
        return max_d

迭代法 层序遍历

最大的深度就是二叉树的层数

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        
        depth = 0
        queue = collections.deque([root])
        
        while queue:
            depth += 1
            for _ in range(len(queue)):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        
        return depth

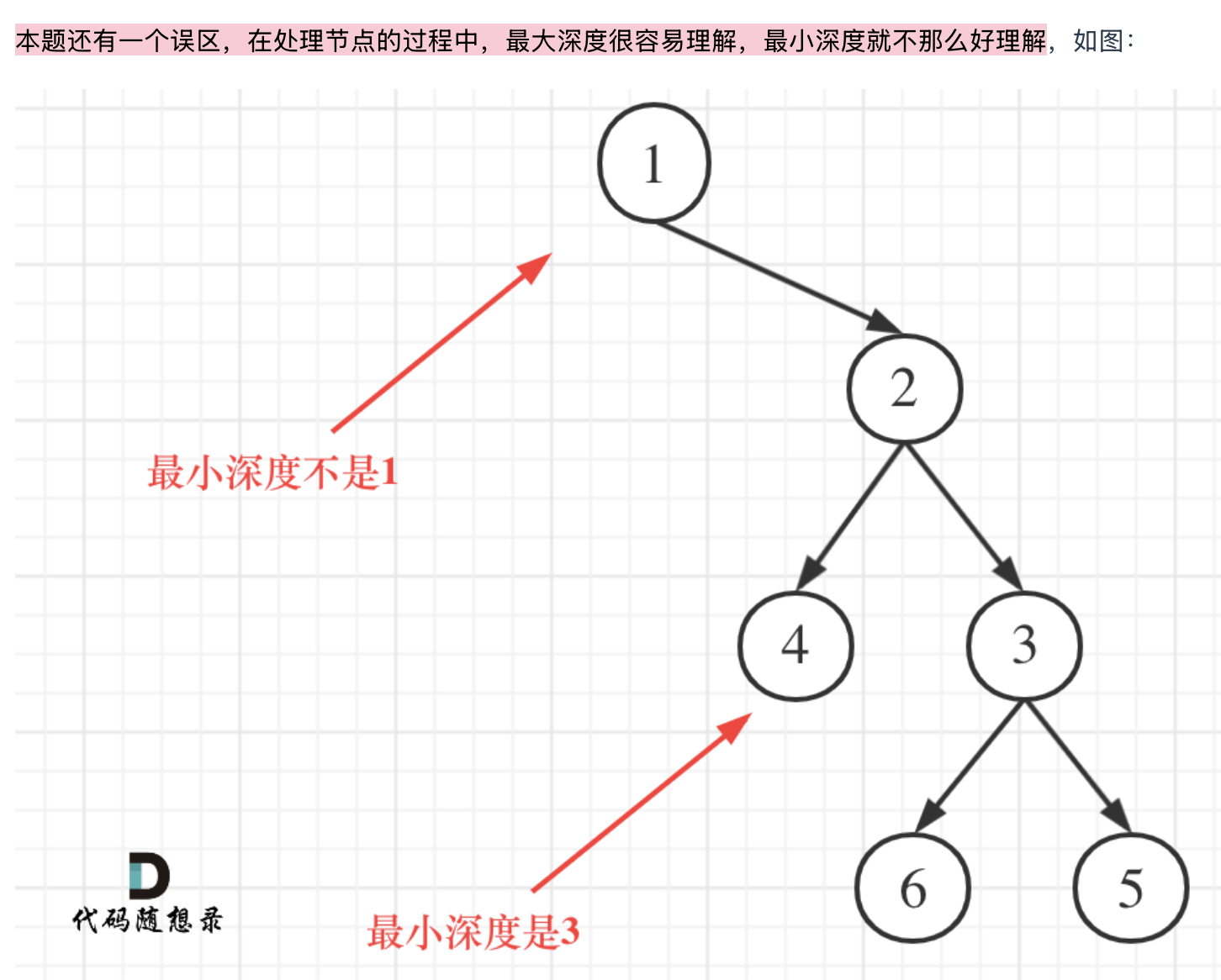
111.二叉树的最小深度 （优先掌握递归）

先看视频讲解，和最大深度 看似差不多，其实 差距还挺大，有坑。

题目链接/文章讲解/视频讲解：https://programmercarl.com/0111.二叉树的最小深度.html

递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def getDepth(self, node):
        if node is None:
            return 0
        leftDepth = self.getDepth(node.left)  # 左
        rightDepth = self.getDepth(node.right)  # 右
        
        # 当一个左子树为空，右不为空，这时并不是最低点
        if node.left is None and node.right is not None:
            return 1 + rightDepth
        
        # 当一个右子树为空，左不为空，这时并不是最低点
        if node.left is not None and node.right is None:
            return 1 + leftDepth
        
        result = 1 + min(leftDepth, rightDepth)
        return result

    def minDepth(self, root):
        return self.getDepth(root)
        

递归法 前序

class Solution:
    def __init__(self):
        self.result = float('inf')

    def getDepth(self, node, depth):
        if node is None:
            return
        if node.left is None and node.right is None:
            self.result = min(self.result, depth)
        if node.left:
            self.getDepth(node.left, depth + 1)
        if node.right:
            self.getDepth(node.right, depth + 1)

    def minDepth(self, root):
        if root is None:
            return 0
        self.getDepth(root, 1)
        return self.result

迭代法 层序遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        depth = 0
        queue = collections.deque([root])
        
        while queue:
            depth += 1 
            for _ in range(len(queue)):
                node = queue.popleft()
                
                if not node.left and not node.right:
                    return depth
            
                if node.left:
                    queue.append(node.left)
                    
                if node.right:
                    queue.append(node.right)

        return depth