代码随想录算法训练营|Day 13

Day 13

理论基础

需要了解 二叉树的种类，存储方式，遍历方式 以及二叉树的定义

文章讲解：https://programmercarl.com/二叉树理论基础.html

二叉树的种类

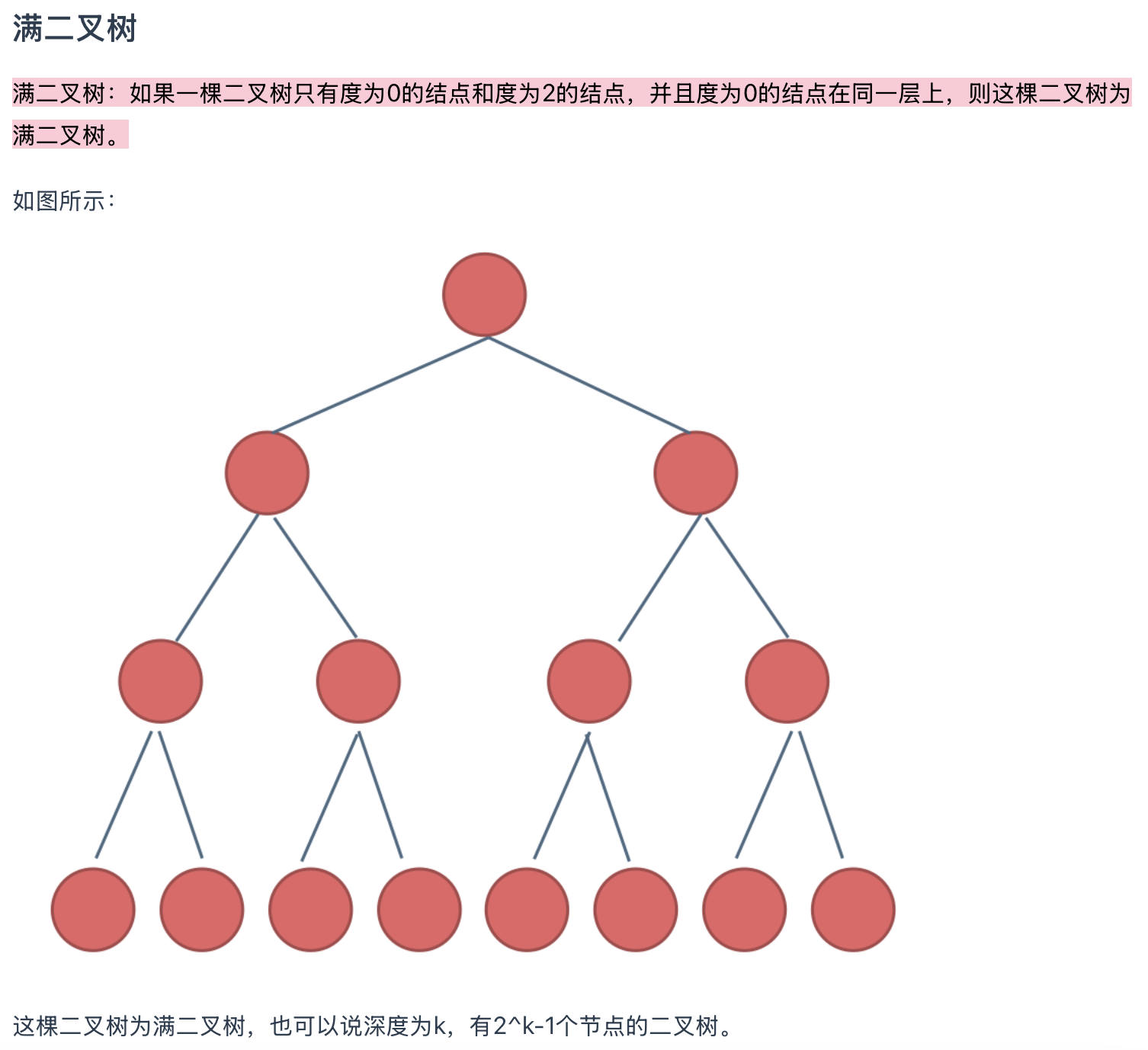
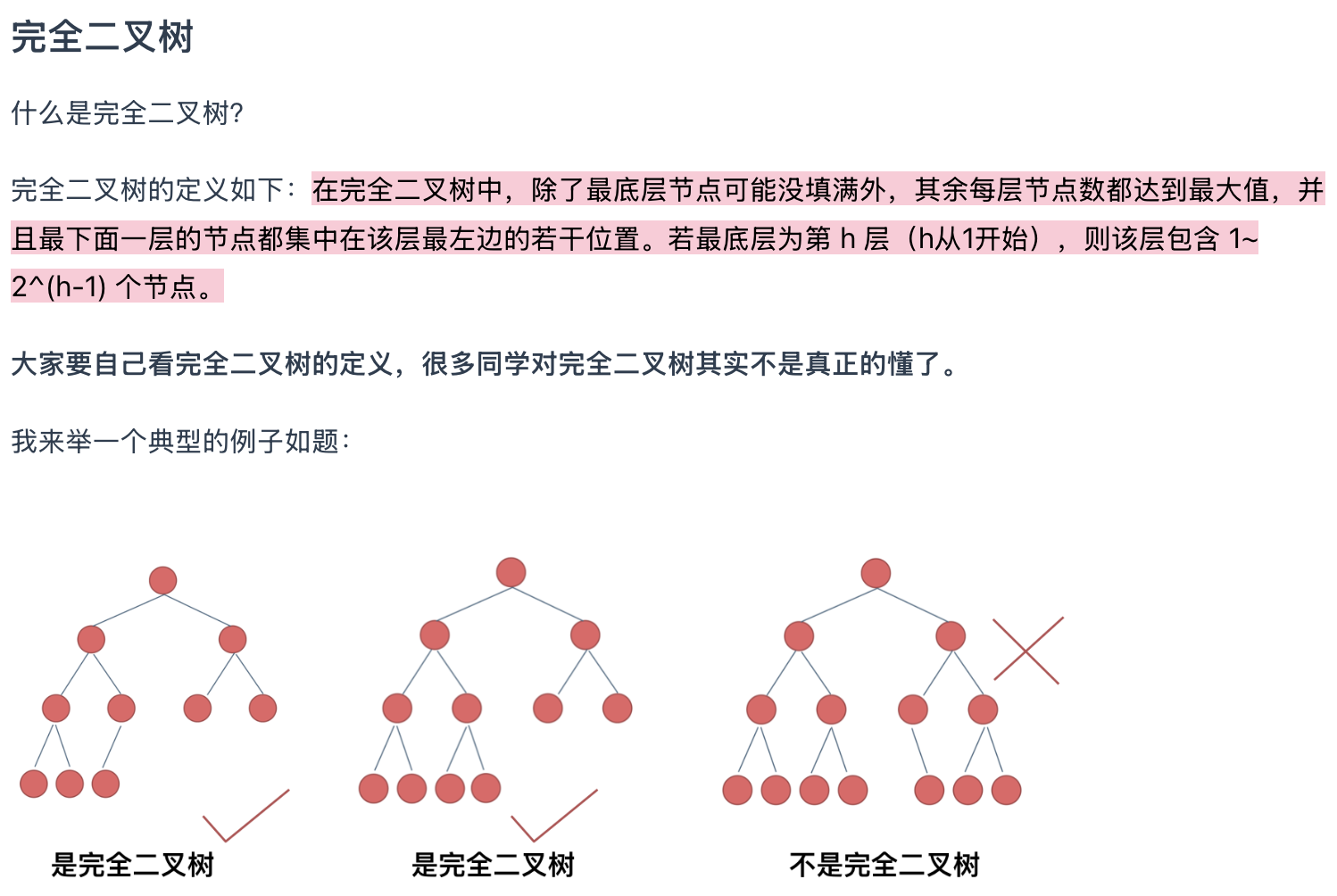
完全二叉树一定是（在leaf节点那层）从左到右连续的

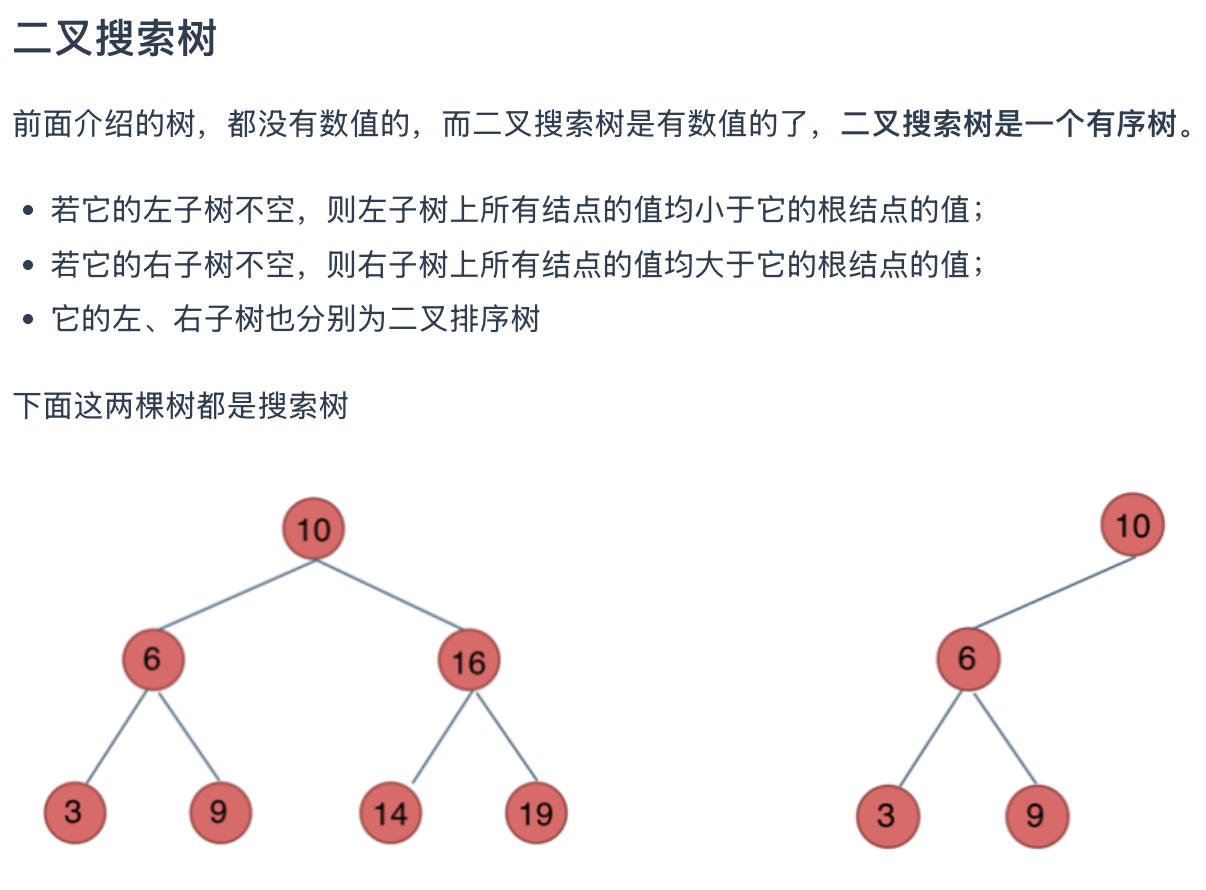
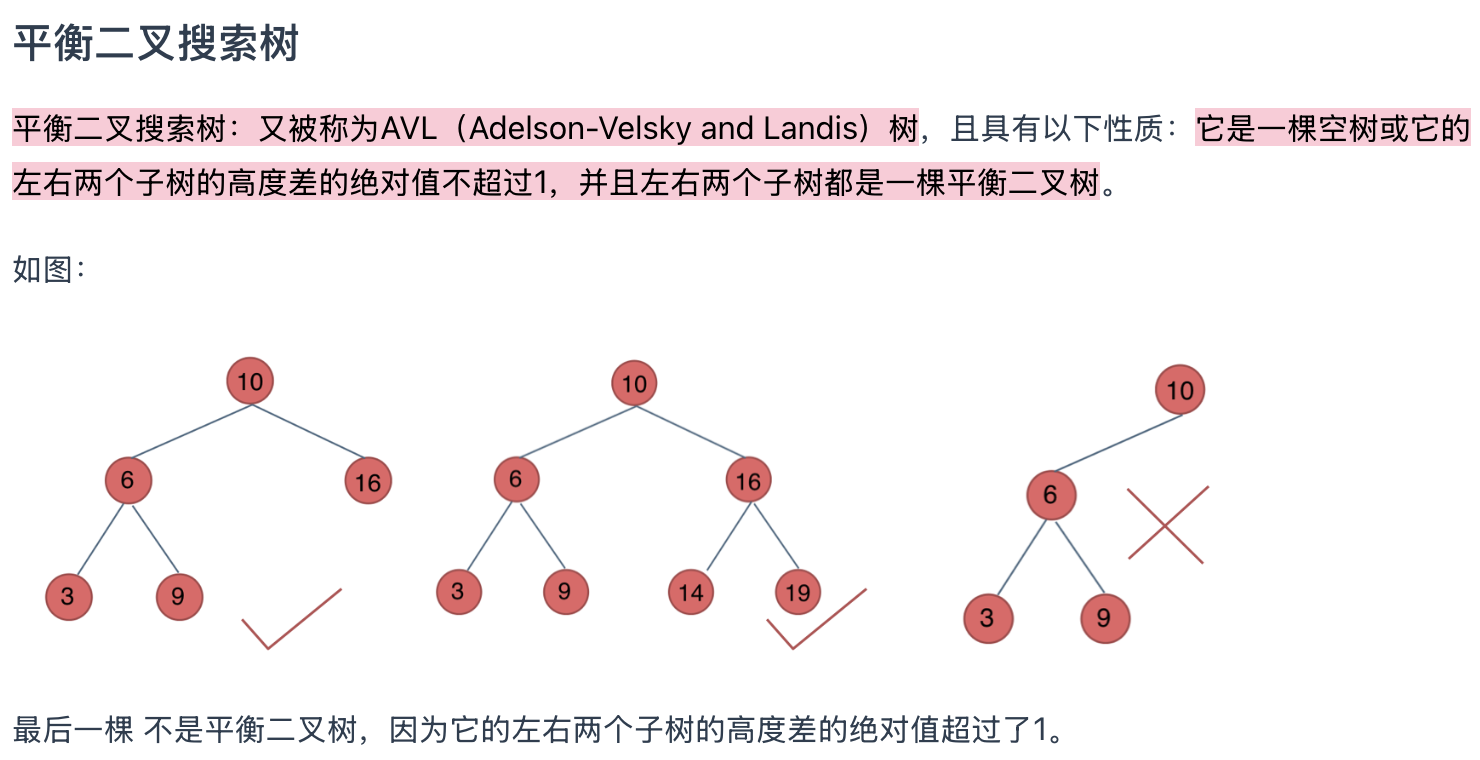
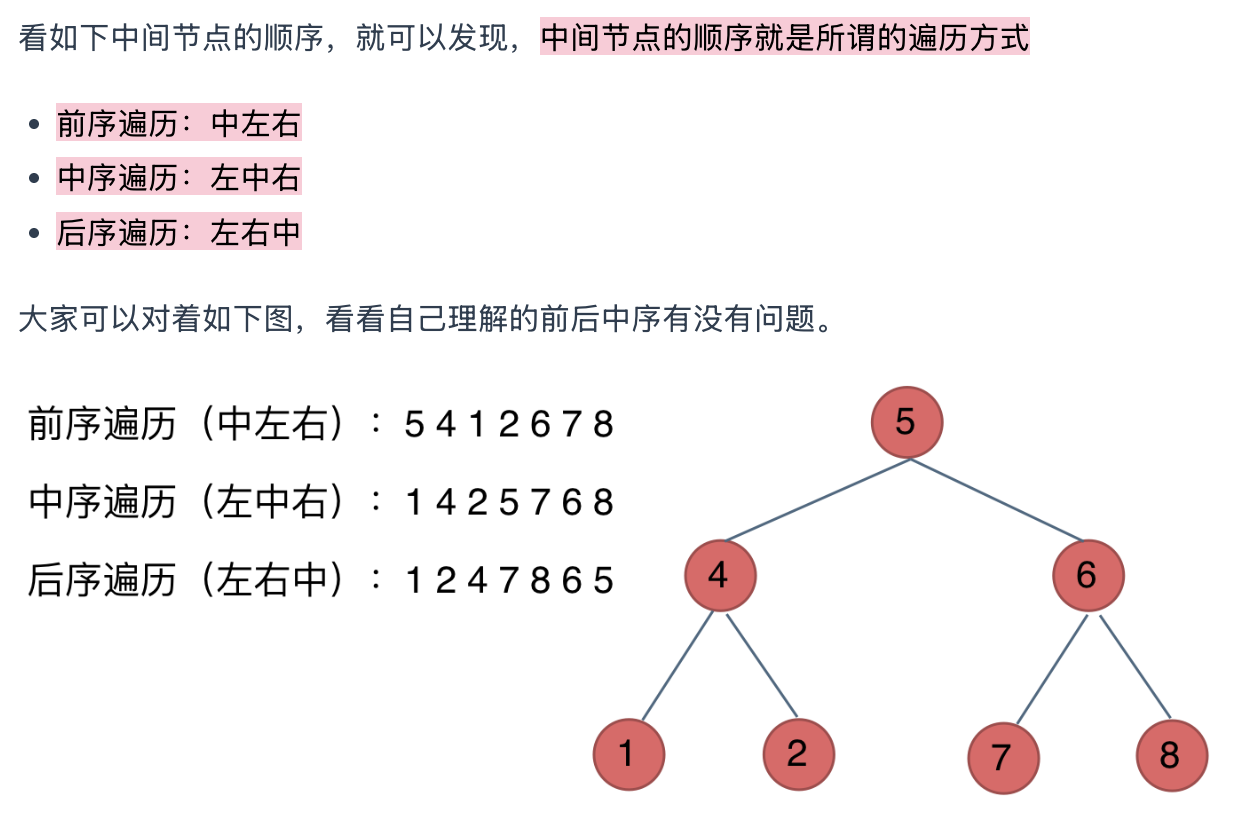
二叉树的遍历

二叉树的定义

class TreeNode:
    def __init__(self, val, left = None, right = None):
        self.val = val
        self.left = left
        self.right = right

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

递归遍历 （必须掌握）

二叉树的三种递归遍历掌握其规律后，其实很简单

题目链接/文章讲解/视频讲解：https://programmercarl.com/二叉树的递归遍历.html

preorder 前序遍历

# 前序遍历-递归-LC144_二叉树的前序遍历
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        
        def dfs(node):
            if node is None:
                return
            
            res.append(node.val)
            dfs(node.left)
            dfs(node.right)
        dfs(root)
        return res

inorder 中序遍历

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        
        def dfs(node):
            if node is None:
                return
            
            dfs(node.left)
            res.append(node.val)
            dfs(node.right)
        dfs(root)
        return res

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []
        return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)

postorder 后序遍历

class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        
        def dfs(node):
            if node is None:
                return
            
            dfs(node.left)
            dfs(node.right)
            res.append(node.val)

        dfs(root)
        return res

if not root:
            return []
        return self.postorderTraversal(root.left) + self.postorderTraversal(root.right) + [root.val]

迭代遍历 （基础不好的录友，迭代法可以放过）

题目链接/文章讲解/视频讲解：https://programmercarl.com/二叉树的迭代遍历.html

前序

class solution:
    def preorderTraversal(self,root:TreeNode)->List[int]:
        # preorder: 中左右
        # 先压右孩子入栈，出栈的时候才是左孩子先出 左->右
        if not root:
            return []
        stack=[root]
        res = []

        while stack:
            node = stack.pop()
            res.append(node.val)
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        return res

中序

先访问根结点，但是首先处理的节点是最最最最...左的那个

class solution:
    def inorderTraversal(self,root:TreeNode)->List[int]:
        # inorder: 左中右
        # 1.遍历 2.处理
        #遍历节点和处理节点是不一样的顺序
        #而对于前序：遍历总是先遍历中，再左右，遍历节点和处理节点顺序一样


        if not root:
            return []

        stack = []
        cur = root
        res = []
        while cur or stack:
            if cur:
                stack.append(cur)
                #一路向左
                cur = cur.left
            else:
                # cur为空，开始从栈里取元素
                cur = stack.pop()
                res.append(cur.val)
                #把中处理完，该向右
                cur = cur.right
        return res

class solution:
    def postorderTraversal(self,root:TreeNode)->List[int]:
        #postorder: 左右 中
        #前序：中左右->调整左孩子右孩子入栈顺序->中右左->反转res数组->后序左右中

        if not root:
            return []
        stack = [root]
        res = []

        while stack:
            node = stack.pop()
            # 中节点先处理
            res.append(node.val)
            # 左孩子先入栈
            if node.left:
                stack.append(node.left)
            #右孩子后入栈
            if node.right:
                stack.append(node.right)
        return res[::-1]

统一迭代 （基础不好的录友，迭代法可以放过）

这是统一迭代法的写法， 如果学有余力，可以掌握一下

题目链接/文章讲解：https://programmercarl.com/二叉树的统一迭代法.html

访问/遍历顺序：都是先访问中节点
处理：前序先访问中节点，而且先处理中节点，可以写出简洁的代码。但中序/后序不可以
统一迭代：
把所有节点都入栈，但是标记中节点表示已访问过，可直接收割/处理
标记：中节点后加入null节点 或者 入栈(node,boolean)元祖，boolean来表示是否已访问
标记：每个节点的最终形态都是中节点。它可能是某个subtree的左or右节点，但当他被标记以后，他就是可以被处理的中节点了

迭代法前序遍历（空指针标记法）

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        # 中 左 右   
        # 按照 右 左 中 入栈
        result = []
        st= []
        if root:
            st.append(root)
        while st:
            node = st.pop()
            if node != None:
                if node.right: #右
                    st.append(node.right)
                if node.left: #左
                    st.append(node.left)
                st.append(node) #中
                st.append(None)
            else:
                node = st.pop()
                result.append(node.val)
        return result

这段代码用的，是一种“标记法”（marker technique）的迭代前序遍历（preorder traversal）实现，核心思路是用一个栈（stack）和一个特殊的空标记 None 来模拟递归时“先访问根，再遍历左子树，最后遍历右子树”的调用顺序。具体流程可以分为以下几步：

1. 初始化

   • result = [] 用来存放最终的遍历结果。
   • st = [] 作为辅助栈，如果 root 不为空就先把它压入 st。

2. 循环弹栈

   • 每次从栈顶 pop 一个元素 node。

   • 如果 node 不是 None，说明这是第一次“来到”这个节点：

     1. 先处理右子节点：如果有 node.right，先把它压入栈中。
     2. 再处理左子节点：如果有 node.left，把它压入栈中。
     3. 然后压入当前节点本身：st.append(node)。
     4. 最后压入一个 None 标记：st.append(None)。

     这样压栈的顺序保证了：当我们下次遇到这个 None 标记时，就意味着“左右子树都已经入栈等待遍历”，该把当前节点的值输出了。

   • 如果 node 恰好是 None，说明这是对上一次压入的那个实际节点的“访问信号”：

     1. 再次 pop() 得到真正的 TreeNode 对象，
     2. 将它的 val 加入 result。

3. 结果输出

   • 当栈空时，所有节点都按“根 → 左 → 右”的顺序被访问过，result 即为前序遍历结果，直接返回。

---

举例说明

假设一棵二叉树：

    1
     \
      2
     /
    3

（即 LeetCode 示例 [1,null,2,3]）

• 初始时 st = [1]
• 弹出 1（非 None）：依次压入 2（右）、无左、再压 1、再压 None → st = [2, 1, None]
• 弹出 None → 再弹出 1 → result = [1]
• 弹出 2：压入（无右）、3（左）、再压 2、再压 None → st = [3, 2, None]
• 弹出 None → 弹出 2 → result = [1,2]
• 弹出 3：压入（无右）、（无左）、再压 3、再压 None → st = [3, None]
• 弹出 None → 弹出 3 → result = [1,2,3]
• 栈空，遍历结束。

这样就得到了前序遍历 [1,2,3]。

---

复杂度分析

• 时间复杂度：每个节点会被压栈和弹栈常数次，整体 O(n)。
• 空间复杂度：最坏情况下栈深度与节点数同量级，O(n)。

这种写法的优点是统一了“访问节点”与“输出节点值”两种操作，用 None 标记区分，逻辑清晰，也很容易改造成中序或后序遍历。

中序 （空指针标记法）

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        # 左 中 右
        # 按 右 中 左入栈
        result = []
        st = []
        if root:
            st.append(root)
        while st:
            node = st.pop()
            if node != None:
                if node.right: #添加右节点（空节点不入栈）
                    st.append(node.right)
                
                st.append(node) #添加中节点
                st.append(None) #中节点访问过，但是还没有处理，加入空节点做为标记。
                
                if node.left: #添加左节点（空节点不入栈）
                    st.append(node.left)
            else: #只有遇到空节点的时候，才将下一个节点放进结果集
                node = st.pop() #重新取出栈中元素
                result.append(node.val) #加入到结果集
        return result

后序 （空指针标记法）

class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        #左 右 中
        #按 中 右 左 入栈
        result = []
        st = []
        if root:
            st.append(root)
        while st:
            node = st.pop()
            if node != None:
                st.append(node) #中
                st.append(None)
                if node.right: #右
                    st.append(node.right)
                if node.left: #左
                    st.append(node.left)
            else:
                node = st.pop()
                result.append(node.val)
        return result

中序遍历（boolean标记法）

class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        #左 中 右
        #按右中左入栈
        values = []
        stack = [(root, False)] if root else [] # 多加一个参数，False 为默认值，含义见下文

        while stack:
            node, visited = stack.pop() # 多加一个 visited 参数，使“迭代统一写法”成为一件简单的事
            
            if visited: # visited 为 True，表示该节点和两个儿子的位次之前已经安排过了，现在可以收割节点了
                values.append(node.val)
                continue

            # visited 当前为 False, 表示初次访问本节点，此次访问的目的是“把自己和两个儿子在栈中安排好位次”。
            # 中序遍历是'左中右'，右儿子最先入栈，最后出栈。
            if node.right:
                stack.append((node.right, False))

            stack.append((node, True)) # 把自己加回到栈中，位置居中。同时，设置 visited 为 True，表示下次再访问本节点时，允许收割

            if node.left:
                stack.append((node.left, False)) # 左儿子最后入栈，最先出栈

        return values

后序遍历， 统一迭代（boolean标记法）

class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        # 左右中
        #按中右左入栈
        values = []
        stack = [(root, False)] if root else [] # 多加一个参数，False 为默认值，含义见下文

        while stack:
            node, visited = stack.pop() # 多加一个 visited 参数，使“迭代统一写法”成为一件简单的事

            if visited: # visited 为 True，表示该节点和两个儿子位次之前已经安排过了，现在可以收割节点了
                values.append(node.val)
                continue

            # visited 当前为 False, 表示初次访问本节点，此次访问的目的是“把自己和两个儿子在栈中安排好位次”
            # 后序遍历是'左右中'，节点自己最先入栈，最后出栈。
            # 同时，设置 visited 为 True，表示下次再访问本节点时，允许收割。
            stack.append((node, True))

            if node.right:
                stack.append((node.right, False)) # 右儿子位置居中

            if node.left:
                stack.append((node.left, False)) # 左儿子最后入栈，最先出栈
        
        return values

层序遍历

看完本篇可以一口气刷十道题，试一试， 层序遍历并不难，大家可以很快刷了十道题。

题目链接/文章讲解/视频讲解：https://programmercarl.com/0102.二叉树的层序遍历.html

使用队列
记录每一层有几个元素，就弹出几个
因为队列里的元素数量不断变化
不记录每层有几个元素（size），会不知道哪些元素属于哪一层

102 二叉树的层序遍历

长度法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        queue = collections.deque([root])
        res = []
        while queue:
            level = []
            for _ in range(len(queue)):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
                level.append(node.val)
            res.append(level)
        return res

在这段代码里，`for _ in range(len(queue)):` 这行其实在**循环开始之前**就把 `len(queue)` 这个值“拍了个快照”——比如此时队列中有 3 个节点，那下面的 `range(3)` 就相当于固定了 `0,1,2`，循环就只会执行 3 次。

—— 尽管在循环体里你不断地做 `popleft()`（出队）和 `append()`（入队），导致 `queue` 的真实长度在变，但这**不会**影响到已经生成好的那个 `range`。
—— 把新加入的子节点放到队尾，是为了在**下一轮** `while queue:` 的时候，再用新的 `len(queue)`（也就是下一层的节点数）来遍历下一层。

简单来说：

1. 每次进入 `while`，先看当前层还有多少节点——`n = len(queue)`。
2. `for _ in range(n)` 只遍历这 n 个节点（即“这一层”）。
3. 循环体里把这 n 个节点出队，并把它们的左右子节点“排队”到队尾。
4. 遍历完这 n 个节点后，`res.append(level)`，`while` 重新检查 `queue`，此时队里就是“下一层”的节点，`len(queue)` 也随之更新。

这样就能保证每次 `for` 只负责“当前这一层”的节点，不会混进下一层的节点数。

递归法

class solution:
    def levelOrder(self, root:Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []


        res = []
        def Traversal(node,level):
            if not node:
                return

            if len(res) == level:
                res.append([])


            res[level].append(node.val)

            Traversal(node.left, level+1)
            Traversal(node.right, level+1)

        
        Traversal(root, 0)
        return res

107 二叉树的层序遍历

将res数组反转即可

199 二叉树的右视图

右视图，就是每层的最后一个加入res

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rightSideView(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        
        queue = collections.deque([root])
        right_view = []
        
        while queue:
            level_size = len(queue)
            
            for i in range(level_size):
                node = queue.popleft()
                
                if i == level_size - 1:
                    right_view.append(node.val)
                
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        
        return right_view

637 二叉树的层平均值

res里收集的是每层val的均值

429 N叉树的层序遍历

收集node.left or node.right变成遍历 node.children

515 在每个树行中找最大值

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def largestValues(self, root: TreeNode) -> List[int]:
        if not root:
            return []

        result = []
        queue = collections.deque([root])

        while queue:
            level_size = len(queue)
            max_val = float('-inf')

            for _ in range(level_size):
                node = queue.popleft()
                max_val = max(max_val, node.val)

                if node.left:
                    queue.append(node.left)

                if node.right:
                    queue.append(node.right)

            result.append(max_val)

        return result

这一行代码的作用是把 max_val 初始化为“负无穷”：

max_val = float('-inf')

• float() 是 Python 的内建函数（built‑in function），用来把一个字符串或数字转换成浮点数（floating‑point number）。
• 当你传入 '-inf' 这个特殊字符串时，float('-inf') 会返回 IEEE 754 标准下的 负无穷（negative infinity）。
• 于是 max_val 就被设为 -∞，在后续的比较里，任何实际的数值（只要不是 NaN）都比 -∞ 要大。

典型用法场景：如果你要在遍历一组数时找最大值，就可以先把 max_val 设为 -∞，这样第一轮比较时，无论当前元素多小，都能把它更新为新的最大值。

max_val = float('-inf')
for x in numbers:
    if x > max_val:
        max_val = x
# 最终 max_val 就是 numbers 里的最大数

要找最小值，就把初始值设为“正无穷”：

min_val = float('inf')
for x in numbers:
    if x < min_val:
        min_val = x
# 最终 min_val 就是 numbers 里的最小值

原理同样基于 IEEE 754 浮点标准：

• float('inf') 表示正无穷（positive infinity），任何实际数值都比它小，第一次比较时就会更新为序列中的第一个元素。
• 之后只要遇到比当前 min_val 更小的值，就继续更新。

116 填充每个节点的下一个右侧节点指针

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""

class Solution:
    def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
        if not root:
            return root
        queue = collections.deque([root])

        while queue:

            prev = None
            for _ in range(len(queue)):

                node = queue.popleft()
                if prev:
                    prev.next = node
                prev = node

                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        return root
        

117 填充每个节点的下一个右侧节点指针II

跟116代码一模一样

104 二叉树的最大深度

递归法

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        # 左子树深度、右子树深度 各加 1，再取最大
        left_d  = self.maxDepth(root.left)
        right_d = self.maxDepth(root.right)
        return 1 + max(left_d, right_d)

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        max_d = 0
        def dfs(node, depth):
            nonlocal max_d
            if not node:
                # 到达空节点，更新 max_d
                max_d = max(max_d, depth)
                return
            # 进入一个新节点，深度 +1
            dfs(node.left,  depth + 1)
            dfs(node.right, depth + 1)

        dfs(root, 0)
        return max_d

层序遍历法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        
        depth = 0
        queue = collections.deque([root])
        
        while queue:
            depth += 1
            for _ in range(len(queue)):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        
        return depth

111 二叉树的最小深度

递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        # 如果没有左子树，只能走右子树
        if not root.left:
            return 1 + self.minDepth(root.right)
        # 如果没有右子树，只能走左子树
        if not root.right:
            return 1 + self.minDepth(root.left)
        # 左右子树都存在，取较小深度
        return 1 + min(self.minDepth(root.left), self.minDepth(root.right))

层序遍历法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        depth = 0
        queue = collections.deque([root])
        
        while queue:
            depth += 1 
            for _ in range(len(queue)):
                node = queue.popleft()
                
                if not node.left and not node.right:
                    return depth
            
                if node.left:
                    queue.append(node.left)
                    
                if node.right:
                    queue.append(node.right)

        return depth