代码随想录算法训练营|Day 11

Day 11

第五章 栈与队列part02

150. 逆波兰表达式求值

本题不难，但第一次做的话，会很难想到，所以先看视频，了解思路再去做题

题目链接/文章讲解/视频讲解：https://programmercarl.com/0150.逆波兰表达式求值.html

遇见数字加入到栈里，遇到操作符开始从栈里弹出（弹出两个元素进行运算）

from operator import add, sub, mul

def div(x, y):
    return int(x/y) if x * y > 0 else -(abs(x)// abs(y))

class Solution:
    def evalRPN(self, tokens: List[str]) -> int:
        stack = []
        ops = {'+':add, '-':sub, '*':mul, '/':div}
        for item in tokens:
            if item in {'+','-','*','/'}:
                ele1 = stack.pop()
                ele2 = stack.pop()
                stack.append(ops[item](ele2,ele1))
            else:
                stack.append(int(item))
        return stack.pop()

239. 滑动窗口最大值 （有点难度，可能代码写不出来，但一刷至少需要理解思路）

之前讲的都是栈的应用，这次该是队列的应用了。

本题算比较有难度的，需要自己去构造单调队列，建议先看视频来理解。

题目链接/文章讲解/视频讲解：https://programmercarl.com/0239.滑动窗口最大值.html

滑动窗口移动一个位置→队列pop出一个元素，再push进一个元素

单调队列：维护队列里单调递增或单调递减

维护出口处是最大值

push进的元素比前面的大，把前面的弹出，直到前面元素没有我这个加入的元素大为止

img

img

img

from collections import deque

class MyQueue:
    def __init__(self):
        self.que = deque()

    def pop(self, value):
        if self.que and value == self.que[0]:
            self.que.popleft()

    def push(self, value):
        while self.que and value > self.que[-1]:
            self.que.pop()
        self.que.append(value)

    def front(self):
        return self.que[0]

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        que = MyQueue()
        res = []
        for i in range(k):
            que.push(nums[i])
        res.append(que.front())
        for i in range(k, len(nums)):
            que.pop(nums[i-k])
            que.push(nums[i])
            res.append(que.front())
        return res

解法二：直接使用单调队列

from collections import deque
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        max_list = [] # 结果集合
        kept_nums = deque() # 单调队列

        for i in range(len(nums)):
            update_kept_nums(kept_nums, nums[i]) # 右侧新元素加入

            if i >= k and nums[i - k] == kept_nums[0]: # 左侧旧元素如果等于单调队列头元素，需要移除头元素
                kept_nums.popleft()

            if i >= k - 1:
                max_list.append(kept_nums[0])

        return max_list

def update_kept_nums(kept_nums, num): # num 是新加入的元素
    # 所有小于新元素的队列尾部元素，在新元素出现后，都是没有价值的，都需要被移除
    while kept_nums and num > kept_nums[-1]:
        kept_nums.pop()

    kept_nums.append(num)

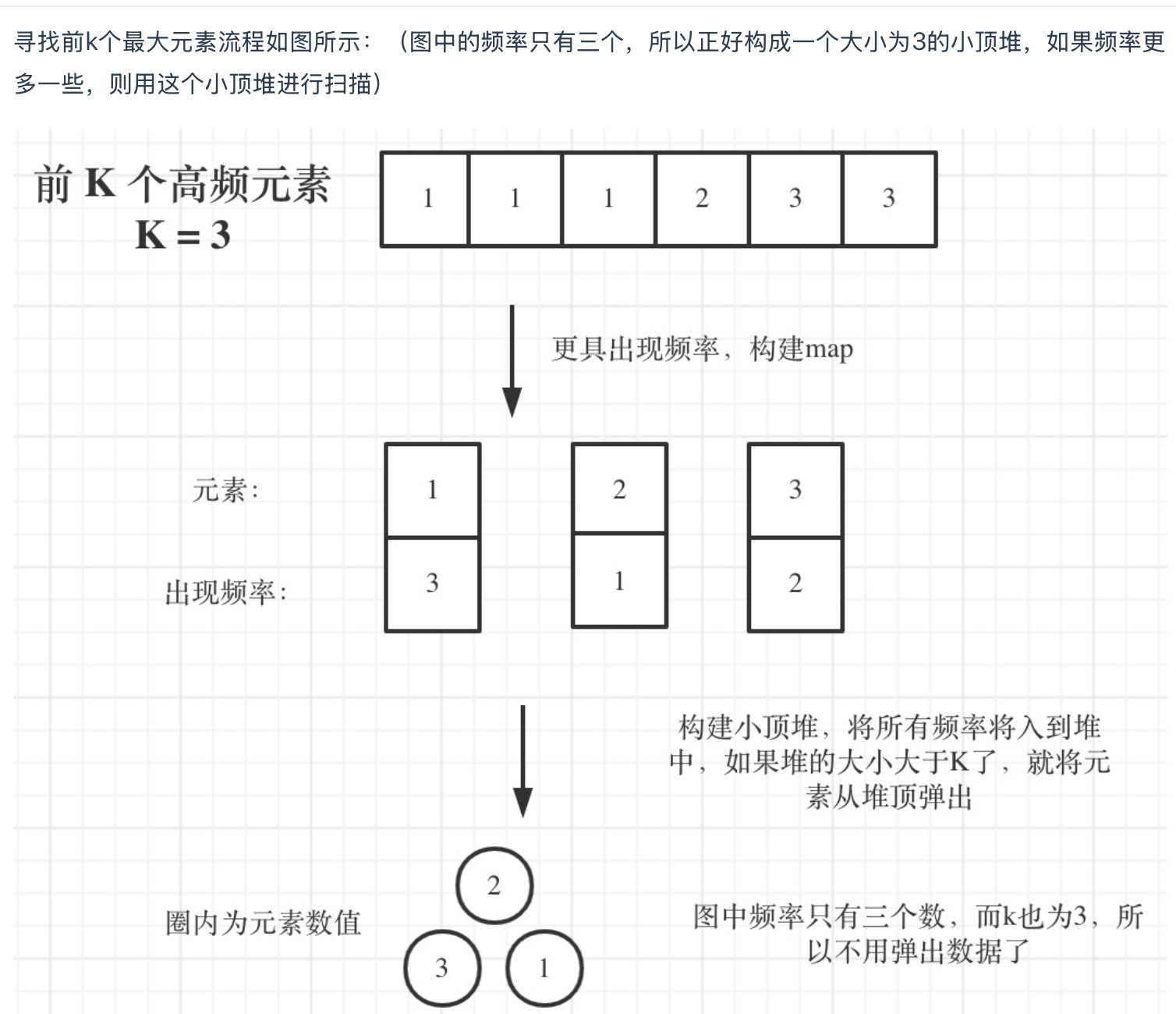
347.前 K 个高频元素 （有点难度，可能代码写不出来，一刷至少需要理解思路）

大/小顶堆的应用， 在C++中就是优先级队列

本题是 大数据中取前k值 的经典思路，了解想法之后，不算难。

题目链接/文章讲解/视频讲解：https://programmercarl.com/0347.前K个高频元素.html

小顶堆，这个堆只维护k个元素
img
img
img

#时间复杂度：O(nlogk)
#空间复杂度：O(n)
import heapq
class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        #要统计元素出现频率
        map_ = {} #nums[i]:对应出现的次数
        for i in range(len(nums)):
            map_[nums[i]] = map_.get(nums[i], 0) + 1
        
        #对频率排序
        #定义一个小顶堆，大小为k
        pri_que = [] #小顶堆
        
        #用固定大小为k的小顶堆，扫描所有频率的数值
        for key, freq in map_.items():
            heapq.heappush(pri_que, (freq, key))
            if len(pri_que) > k: #如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
                heapq.heappop(pri_que)
        
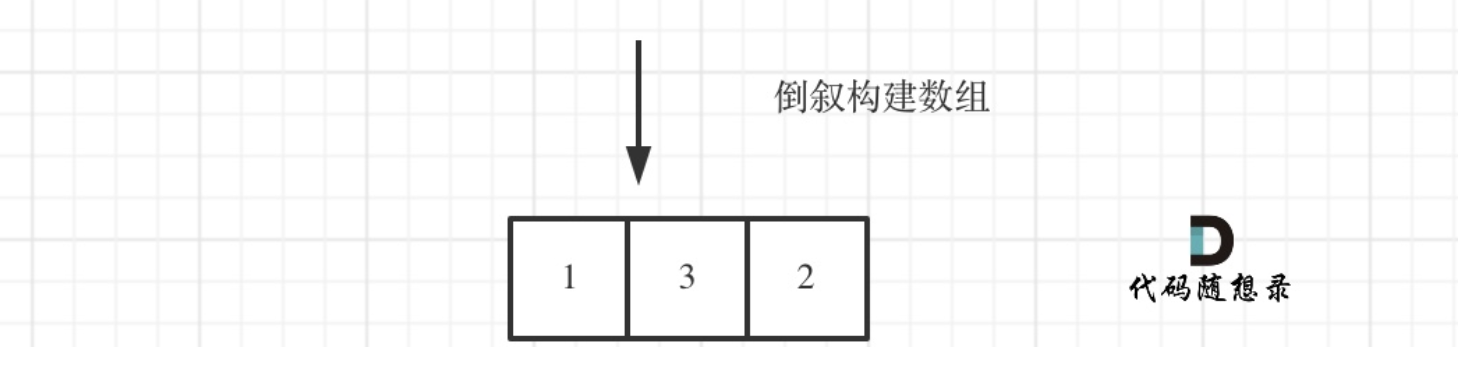
        #找出前K个高频元素，因为小顶堆先弹出的是最小的，所以倒序来输出到数组
        result = [0] * k
        for i in range(k-1, -1, -1):
            result[i] = heapq.heappop(pri_que)[1]
        return result

总结

栈与队列做一个总结吧，加油

https://programmercarl.com/栈与队列总结.html

posted @ 2025-07-13 21:07  ForeverEver333  阅读(10)  评论(0)    收藏  举报