算法总结

三大基本简单算法

1、冒泡排序算法

　　冒泡排序，排序n个数据。

　　第一次循环，拿下标为0的开始和下标为1的进行比较，拿这两个中比较大的赋值给下标为1的位子，再对下标为1，2的数据进行比较，把大的赋值给下标为2的，以此类推，则最后一个数据就是第一次遍历出的最大的数据。

　　第二次循环用同样的方法，但是只用排序前（n-1）个数据。

　　......

　　第（n-m）次循环，只用循环前m个数据，因为之后的数据已经有序了。

　　进行（n-1)次循环之后，数据就呈有序排列了。

def maopao(li):
    for i in range(len(li)-1):
        exchange = False
        for s in range(len(li)-1-i):
            if li[s] > li[s+1]:
                li[s],li[s+1] = li[s+1],li[s]
                #一趟下来没有交换，说明已经达到有序状态
                exchange = True
        if not exchange:
            break

　　

2、选择排序算法

　　选择排序，排序n个数据。

　　第一次循环，对数据进行比较，找到最大数据的下标，将最大数据和最后一个数据进行互换。互换后数据的最后一个数据已经是最大数据了。所以下一个循环排序不用带上最后一个数据。只循环前（n-1）个数据。

　　第二次循环，对前（n-1）个数据进行比较，找到最大数据的下标，将最大数据和第（n-1）个数据进行互换。下一次循环再减去一个数据。

　　......

　　第（n-m）次循环，只用循环前m个数据，因为之后的数据已经有序了。

　　进行（n-1)次循环之后，数据就呈有序排列了。

def pailie(li):
    for i in range(len(li)-1):
        minli = i
        for s in range(len(li)-1-i):
            if li[minli] > li[i+s+1]:
                minli = i+s+1
        li[minli],li[i] = li[i],li[minli]

　　

3、插入排序算法

　　插入排序，排序n个数据。

　　第一次循环，对前两个数据进行比较，如果第二个数据比第一个小，则第一个数据挪到第二个位子，第二个数据插入到第一个位子。

　　第二次循环，拿到第三个数据，先和第二个数据进行比较，如果第二个数据大的话，就往后挪一个位子，再用拿到的第三个数据和第一个数据进行比较，选择插入位置。

　　......

　　第（n-m）次循环，拿到第（n-m+1）个数据，对直接的每一个数据进行比较，如果比拿到的数据大就往后挪一位，直到找到合适的位置插入。这样的话，前（n-m）的数据呈有序

　　进行（n-1)次循环之后，数据就呈有序排列了。

def inser_sort(li):
    for i in range(1,len(li)):
        tem = li[i]
        j = i-1
        while j >=0 and li[j] > tem:
            li[j+1] = li[j]
            j = j-1
        li[j+1] = tem

　　

快排、堆排、归并、希尔排序

1、快排算法

　　快排思路：

　　　　先选取一个元素p（第一个元素），使p元素归位。

　　　　列表被p分为两部分，左边都是比p小的，右边都是比p大的。

　　　　递归完成排序。

　　

#快排队列
def fast_sort(li,left,right):
    if left < right:
        # 按照下标为left将数据分为左右两份
        men = sort_x(li,left,right)
        #再将左右两份分表根据他们的第一个元素进行分类
        fast_sort(li,left,men-1)
        fast_sort(li,men+1,right)
        #每一份都进行递归，直至只有一个元素，此时返回的数组已经排序完成
        
def sort_x(li,left,right):
    #取第一个元素
    tem = li[left] 
    #对数据进行分类，把小于tem的数据放在左边，大于tem的数据放在右边
    while left < right:
        while left < right and tem <= li[right]:
            right -= 1
        li[left] = li[right]
        while left < right and tem >= li[left]:
            left += 1
        li[right] = li[left]
    li[left] = tem
    #返回最后tem的下标
    return left

#启动排序，传入left = 0；right = len(li)-1
def fast_sort_x(li):
    fast_sort(li,0,len(li)-1)

2、堆排序

　　堆排序是利用二叉树性质进行的一种排序。

　　二叉树是度不超过2的树

　　满二叉树与完全二叉树

　　（完全）二叉树可以用列表来存储，通过规律可以从父亲找到孩子或从孩子找到父亲

　　步骤：

　　　　1.建立堆

　　　　2.得到堆顶元素，为最大元素

　　　　3.去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。

　　　　4.堆顶元素为第二大元素。

　　　　5.重复步骤3，直到堆变空。

#堆排列
def sift(data,low,high):
    i = low         #父节点
    j = 2*i +1      #父节点的做左子节点
    tem = data[i]
    while j <= high:
        if j+1 <= high and data[j+1]>data[j]:
            j +=1   #求出左右子节点的大的那一个
        if tem < data[j]:   #如果子节点比父节点大
            data[i] = data[j]   #子节点转移到父节点  并继续对子节点进行比较
            i = j
            j = 2*i+1
        else:    #子节点比父节点小 ，不进行变化
            break
    data[i] = tem

def heap_sort(data):
    n = len(data)
    #初始化堆，先使堆有序
    for i in range(n//2 -1,-1,-1):
        sift(data,i,n-1)
    #开始取数据，每次取最大的数据放在最后，并拿一个末尾的数据到堆顶，并进行排序。
    for j in range(n-1,0,-1):
        data[j],data[0] = data[0],data[j]
        sift(data,0,j-1)
    #循环完毕，完成排序

3、归并排序

　　假设数据分为左右两个有序数据，将其合为一个有序数据的过程就是归并排序。

　　其过程为将数据一直细分为左右两份数据。

　　运用递归一直细分到每一边只有一个数据，则细分数据其现在呈有序状态。

　　之后在对数据进行合并，运用递归，合并为一份数据，则其按照规则合并后已经呈有序。

#归并排列
def merge(data,low,mid,high):
    li = []
    i = low
    j =mid+1
    #数据根据mid的位置左右分别有序，对左右两份数据进行合并
    while i <=mid and j <=high:
        if data[i] > data[j]:
            li.append(data[j])
            j += 1
        else:
            li.append(data[i])
            i += 1
    #如果右边没有数据了，就直接将左边数据加入新数据右边
    while i <= mid:
        li.append(data[i])
        i +=1
    # 如果左边没有数据了，就直接将右边数据加入新数据右边
    while j <= high:
        li.append(data[j])
        j +=1
    #将新建立的数据集合赋值给原数组，排序完成
    data[low:high+1] = li

def _merge_sort(data,low,high):
    if low <high:
        #初始中间位置设为数据中间
        mid = (low+high)//2
        #数据左边拆分
        _merge_sort(data,low,mid)
        # 数据左边拆分
        _merge_sort(data,mid+1,high)
        #数据合并排序，用到递归思想
        merge(data,low,mid,high)

def merge_sort(data):
    _merge_sort(data,0,len(data)-1)

4、希尔排序

　　希尔排序是插入排序的一种优化方案。

　　就是先对数据分组进行插入排序，每次循环分组减少一倍，使数据基本按照大小顺序怕分布在数据的左右两边。

　　左后对数据进行插入排序时不用移动很多元素，可以很快将数据排出来。

#希尔排列
def shell_sort(data):
    #分的组数
    gap = len(data) // 2
    #只要分组数>1,就分别对每组进行插入排序
    while gap>=1:
        for i in range(gap,len(data)):
            tem = data[i]
            j = i - gap
            while j >= 0 and data[j] > tem:
                data[j+gap] = data[j]
                j = j - gap
            data[j+gap] = tem
        #排序完成，将分组数减少一倍
        gap //= 2

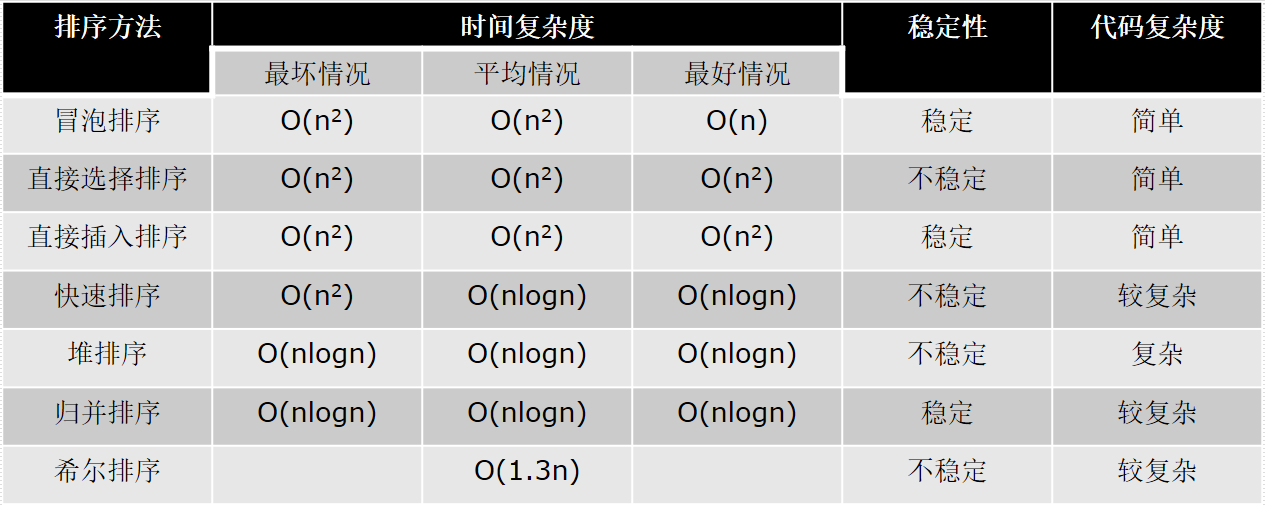
各种排序算法的时间复杂度和稳定性

　　时间复杂度：计算所用的时间长短

　　稳定性：遇到相等的元素，是否进行交换，交换的话，就不稳定

　

算法练习题

1、习题一

　　现在有一个列表，列表中的数范围都在0到100之间，列表长度大约为100万。设计算法在O(n)时间复杂度内将列表进行排序。

　　解析：

　　　　虽然数据很多，但是他们的值的数量很小，就新建一个数组，把下标看作对应的值，统计每个数字出现的次数，输出是按照大小输出对应的次数即可。

 

def count_sort(data,max_num):
    #创建一个长度为max_num的全部值为0的列表
    list = [0 for i in range(max_num+1)]
    for i in data:
        #循环数据，每取一个数据，在list列表中下表为i的那个值加一
        list[i] += 1
    i = 0
    for num,n in enumerate(list):
        #循环list列表，每一个下标的值为几，就输出几次这个值。
        for j in range(n):
            data[i] = num
            i +=1

2、习题二

　　现在有n个数（n>10000），设计算法，按大小顺序得到前10大的数。

　　应用场景：榜单TOP 10

　　解析：

　　　　因为只要最大的十个数，所以没有必要将整个数据进行排序，因为剩下的数据是否有序不影响结果。

　　　　所以可以新建一个数量为10的数组，并将这个数组进行排序，使其有序。

　　　　然后从第11位开始取数据，拿取到的数据和十位的列表中的最小的那个做比较，如果不够大就继续循环取数，如果比最小的数大，就把取出的数据覆盖掉最小的数，并再对十位的数组排序。直至数据取完，十位数组里面储存的就是最大的十个数字。

　　　　按照这个思路可以用插入排序或者堆排序实现，下面用的是插入排序。

#将一个数组按照左大右小顺序排好
def inser_sort(list):
    for i in range(1,len(list)):
        tem = list[i]
        j = i-1
        while j >=0 and list[j] < tem:
            list[j+1] = list[j]
            j = j-1
        list[j+1] = tem

def topk(li,k):
    list = li[0:k]    #创建一个长度为k的数组来储存最大的k个数
    inser_sort(list)     #将这个K数组先按照大小顺序用插入偶排序排好
    print(list)
    print(list[-1])

    for i in range(k,len(li)):    #将剩下的数字依次拿到
        #将拿到的数字和数组中最小的数字做对比
        if li[i] > list[-1]:    #如果比最小的数字大，就做交换，把最小的数字换成取到的数
            list[-1] = li[i]
            #交换之后进行排序
            inser_sort(list)
    print(list)