Matlab传递函数的根轨迹曲线的绘制以及如何确定图得出闭环系统稳定的根轨迹系数 5

一、题目与代码及实验结果

题目：

代码：

clc ;clear all;close all;
%G1(S)
 num1=[1];
 temp1=[1,0];
 temp2=[1 2 2];
 temp3=[1 6 13];
 temp=conv(temp1,temp2);
 den1=conv(temp,temp3);
 figure;
 rlocus(num1,den1); grid
 title('G1(s)的根轨迹');
  G=tf(num1,den1);
  [k,r]=rlocfind(G);%或者[k,r]=rlocfind(num1,den1);
 %G1(s)的单位负反馈的阶跃响应
 figure
G1_c=feedback(G,1);
step(G1_c);grid
xlabel('t/s');
ylabel('G1_c(t)')
title('G1(s)的单位负反馈的阶跃响应');


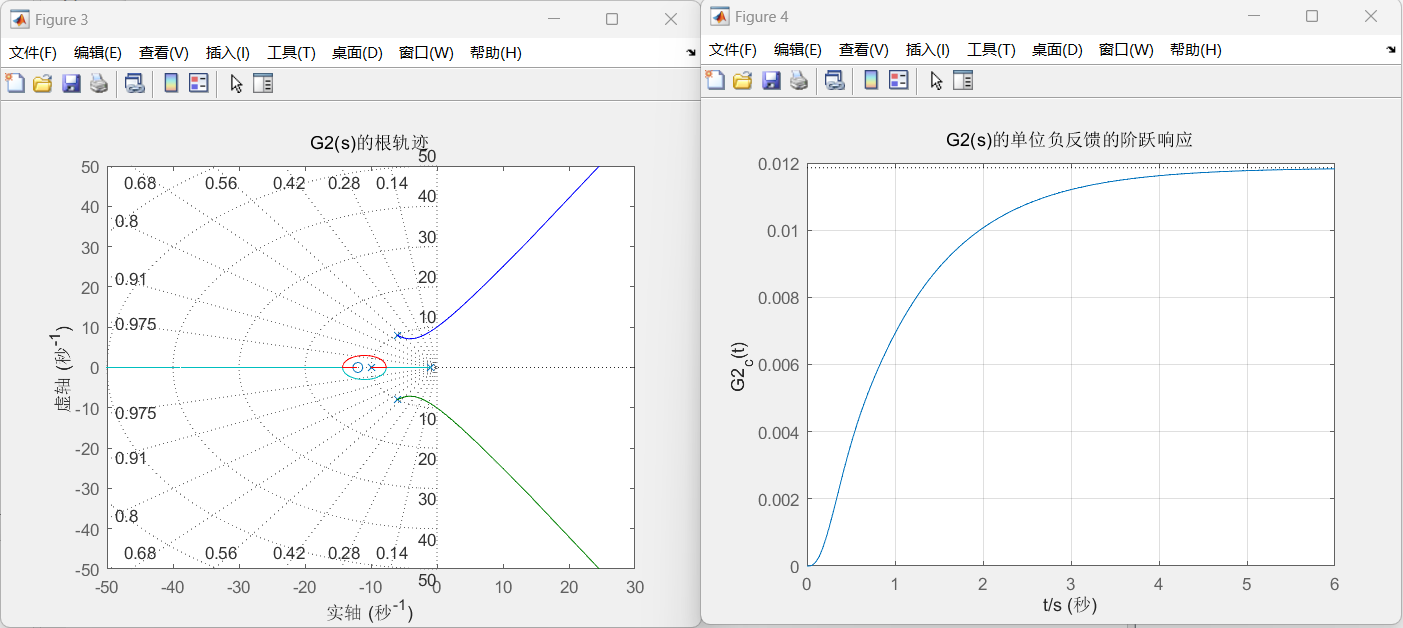
%G2(S)
 num1=[1,12];
 temp1=[1,1];
 temp2=[1 12 100];
 temp3=[1 10];
 temp=conv(temp1,temp2);
 den1=conv(temp,temp3);
 figure;
 rlocus(num1,den1); grid
 title('G2(s)的根轨迹');
  G=tf(num1,den1);
 [k,r]=rlocfind(G);%或者[k,r]=rlocfind(num1,den1);
 %G2(s)的单位负反馈的阶跃响应
 figure
G2_c=feedback(G,1);
step(G2_c);grid
xlabel('t/s');
ylabel('G2_c(t)')
title('G2(s)的单位负反馈的阶跃响应');


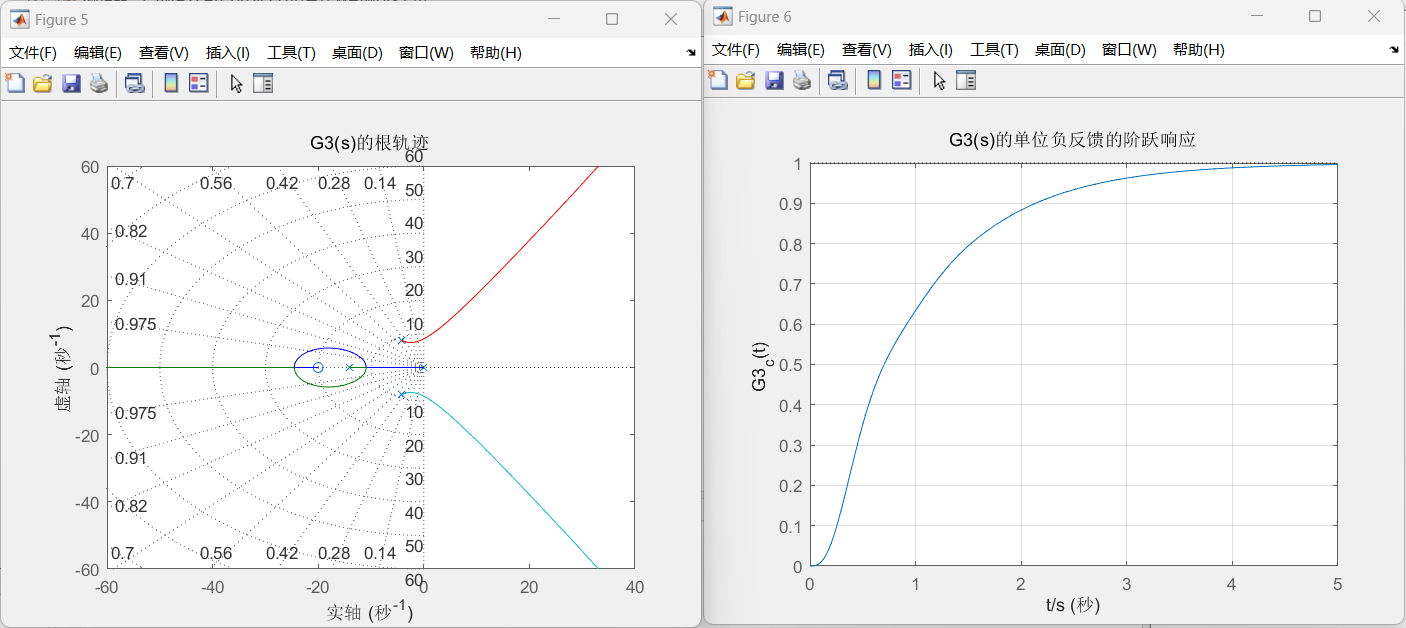
%G3(S)
 num1=[0.05,1];
 temp1=[1,0];
 temp2=[0.0714 1];
 temp3=[0.012 0.1 1];
 temp=conv(temp1,temp2);
 den1=conv(temp,temp3);
 figure;
 rlocus(num1,den1); grid
 title('G3(s)的根轨迹');
  G=tf(num1,den1);
 [k,r]=rlocfind(G);%或者[k,r]=rlocfind(num1,den1);
 %G3(s)的单位负反馈的阶跃响应
 figure
G3_c=feedback(G,1);
step(G3_c);grid
xlabel('t/s');
ylabel('G3_c(t)')
title('G3(s)的单位负反馈的阶跃响应');

实验结果：

---

二、关键函数详解

1. 清理与初始化函数

clc; clear all; close all;

• clc：清空命令窗口，让屏幕更整洁。
• clear all：删除工作区中所有的变量，避免之前的计算结果干扰当前程序。
• close all：关闭所有已经打开的图形窗口，防止多个图重叠。

这是 MATLAB 程序开头的标准 “清洁” 操作，确保一个干净的工作环境。

---

2. 传递函数构建函数

tf(num, den)

• 功能：创建一个线性时不变（LTI）系统的传递函数模型。
• 用法：G = tf(num, den)
  • num：分子多项式的系数向量，按 s 的降幂排列。
  • den：分母多项式的系数向量，按 s 的降幂排列。
• 示例：在 G₁(s) 中

  num1 = [1];
  den1 = [1 8 25 26 26];
  G = tf(num1, den1);
  

  这行代码创建了传递函数

---

3. 根轨迹绘制函数

rlocus(G) 或 rlocus(num, den)

• 功能：计算并绘制系统的根轨迹图。根轨迹是当系统的某个参数（通常是开环增益 K）从 0 变化到无穷大时，闭环系统特征方程的根在 s 平面上移动的轨迹。
• 用法：
  • rlocus(G)：直接使用传递函数对象 G。
  • rlocus(num, den)：使用分子和分母系数向量。
• 输出：一张根轨迹图，其中：
  • 蓝色的 × 标记开环极点（Open-loop Poles）。
  • 红色的 ○ 标记开环零点（Open-loop Zeros）。
  • 黑色的曲线就是根轨迹。
• 示例：

  rlocus(num1, den1);
  

  这条命令会绘制出 G₁(s) 对应的根轨迹。

---

4. 反馈连接函数

feedback(G, H)

• 功能：将两个系统 G 和 H 进行反馈连接，默认情况下是负反馈。
• 用法：closed_loop_G = feedback(G, H)
  • G：前向通道的传递函数。
  • H：反馈通道的传递函数。
• 计算逻辑：闭环传递函数
• 示例：

  G1_c = feedback(G, 1);
  

  这里 H = 1，表示单位负反馈。

---

5. 阶跃响应仿真函数

step(G)

• 功能：计算并绘制系统在单位阶跃输入下的响应曲线。
• 用法：step(G)
  • G：通常是闭环系统的传递函数。
• 输出：一张阶跃响应图，其中：
  • 横坐标是时间 t。
  • 纵坐标是系统输出 y(t)。
• 示例：

  step(G1_c);
  

  这条命令会仿真并绘制出闭环系统 G₁_c (s) 的单位阶跃响应。

---

6. 图形美化函数

• figure：创建一个新的图形窗口，用于绘制新的图。
• grid：在图形上添加网格线，方便读取数据。
• title('文本')：为图形添加标题。
• xlabel('文本')：为图形的 x 轴添加标签。
• ylabel('文本')：为图形的 y 轴添加标签。

---

三、代码结构分析

整个代码的结构非常清晰，采用了重复的模式来分析三个不同的系统：

对每个系统（G₁, G₂, G₃）都执行以下步骤：

1. 定义传递函数：

   • 指定分子 num1 和分母 den1 的系数。
   • 分母的构建使用了 conv 函数（多项式乘法），因为分母通常是多个因式的乘积。
   • 例如，den1 = conv(conv(temp1, temp2), temp3); 等价于 den1 = temp1 * temp2 * temp3（多项式乘法）。

2. 绘制根轨迹：

   • 使用 figure 创建新窗口。
   • 使用 rlocus 绘制根轨迹。
   • 使用 grid、title 等函数美化图形。

3. 创建闭环系统：

   • 使用 tf 函数将分子分母包装成传递函数对象 G。
   • 使用 feedback(G, 1) 创建单位负反馈的闭环系统 G_c。

4. 仿真阶跃响应：

   • 使用 figure 创建另一个新窗口。
   • 使用 step 函数仿真并绘制阶跃响应。
   • 使用 grid、title、xlabel、ylabel 等函数美化图形。

总结

1. 绘制根轨迹图：分析当系统增益 K 从 0 变化到无穷大时，闭环系统特征根在 s 平面上的移动轨迹。
2. 绘制阶跃响应曲线：在单位负反馈条件下，给系统输入一个单位阶跃信号，观察系统输出随时间的变化。

1. 建模：tf
2. 分析：rlocus（稳定性分析）、step（动态性能分析）
3. 连接：feedback