SDN_Laboratory Homework

这是三次作业的合集，全部放一起交咯。在开始这个作业之前，我先去自己学习了一下计网的相关知识，并查询scapy的相关资料。我把笔记放在代码仓库的根目录里了。>GitHub笔记链接

可编程网络实验室2023暑期纳新——第一次作业

这个作业属于哪个课程	2023暑假作业
这个作业要求在哪里	可编程网络实验室2023暑期纳新——第一次作业
这个作业的目标	学习git，虚拟机的创建和ping通，安装相关环境

自我介绍

吴荣榜	2022级计算机与大数据学院软件工程3班
	wurongbang@foxmail.com
	https://github.com/ROBINRUGAN

代码仓库

https://github.com/ROBINRUGAN/SDN_Laboratory

安装虚拟机

由于我以前下载过VMware，直接打开进入虚拟机的配置。直接选择典型创建，后面要改可以去设置里改。

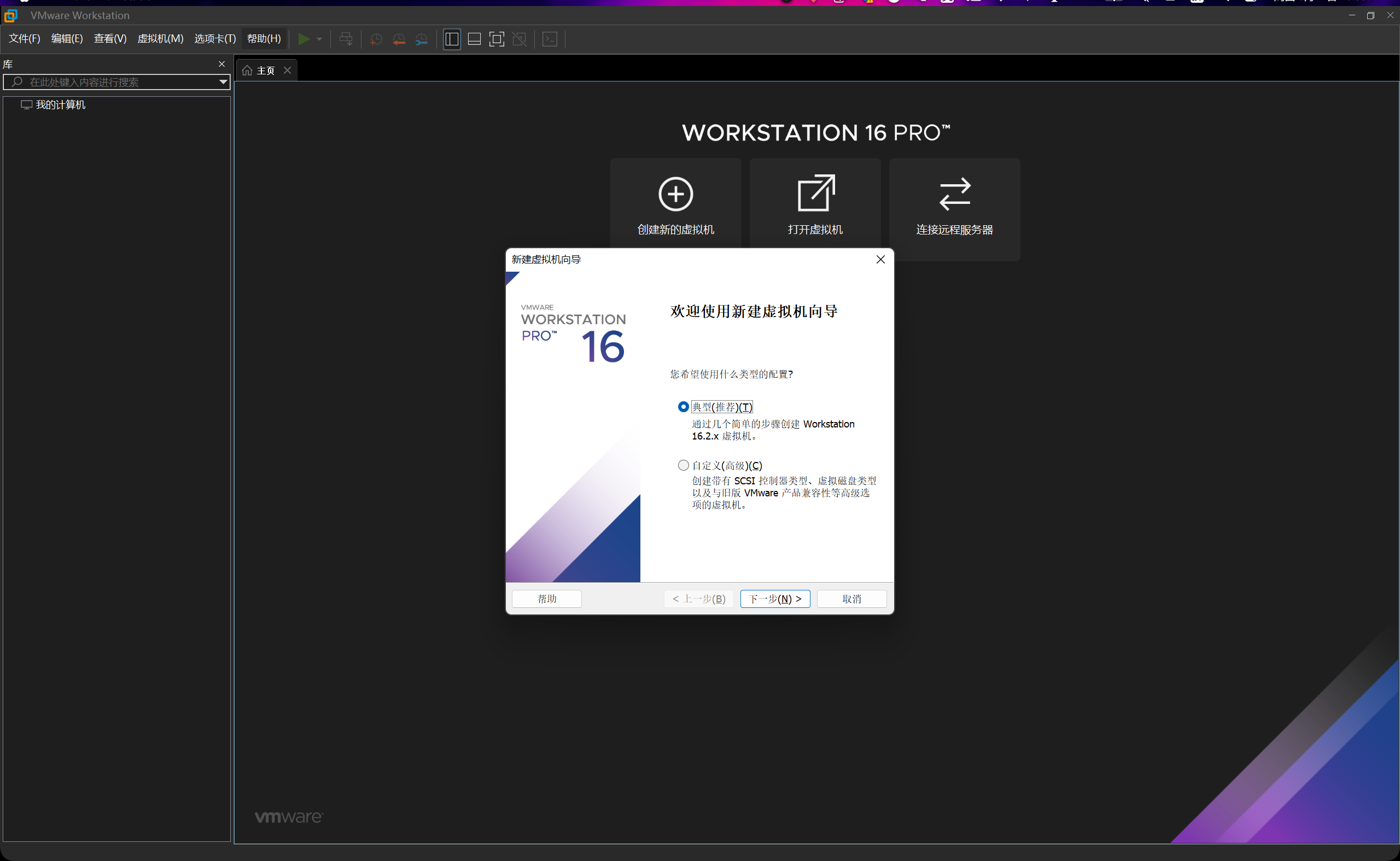
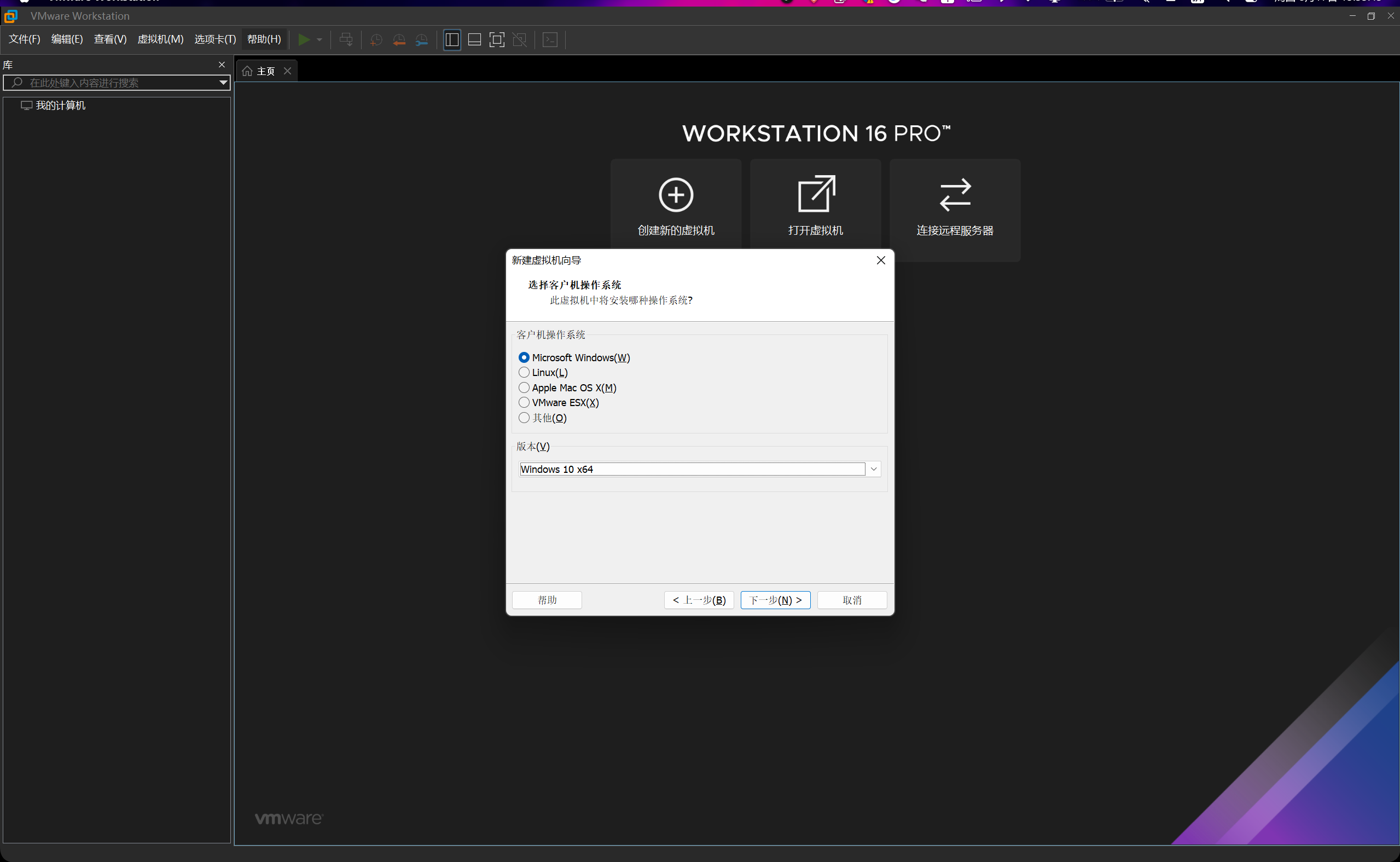
我们选择创建一台Windows 10 64位的虚拟机。

全部点完之后，虚拟机准备就绪，然后我们接下来准备好win10对应的iso镜像。

我们到微软的官网下载一个下载工具，最下面那个就是，然后下载完后，根据界面指令，安装好对应的iso。或者也可以上福州大学网信办官网下载对应的iso。

iso下载好后，直接打开虚拟机设置，然后切换到光驱的选项卡。选择我们刚才下载好的镜像，然后保存，启动虚拟机。

启动时可能会有一句提示说press any key来运行CD/DVD的，随便按个按键即可进入。

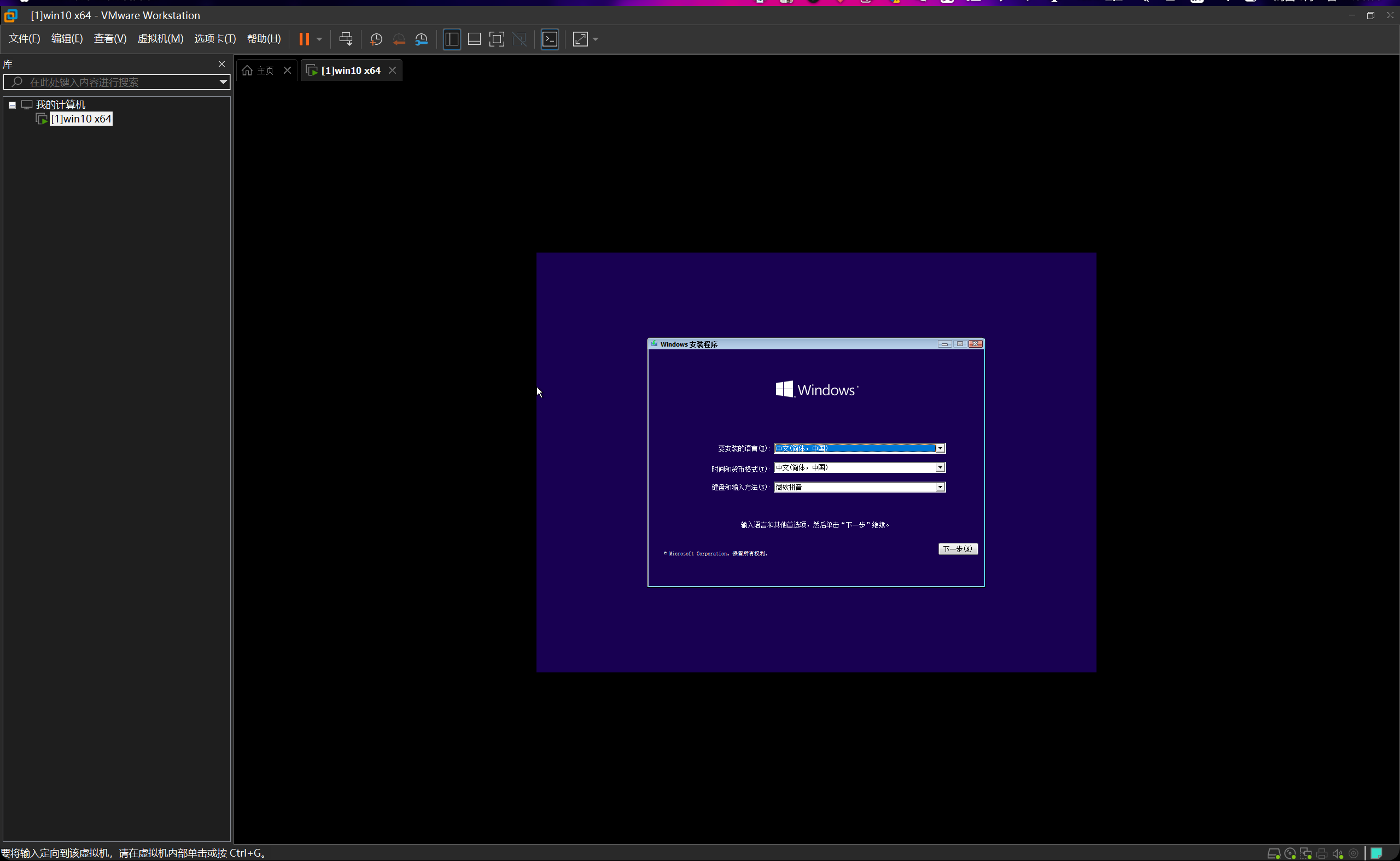
这个地方我们要选择自定义。

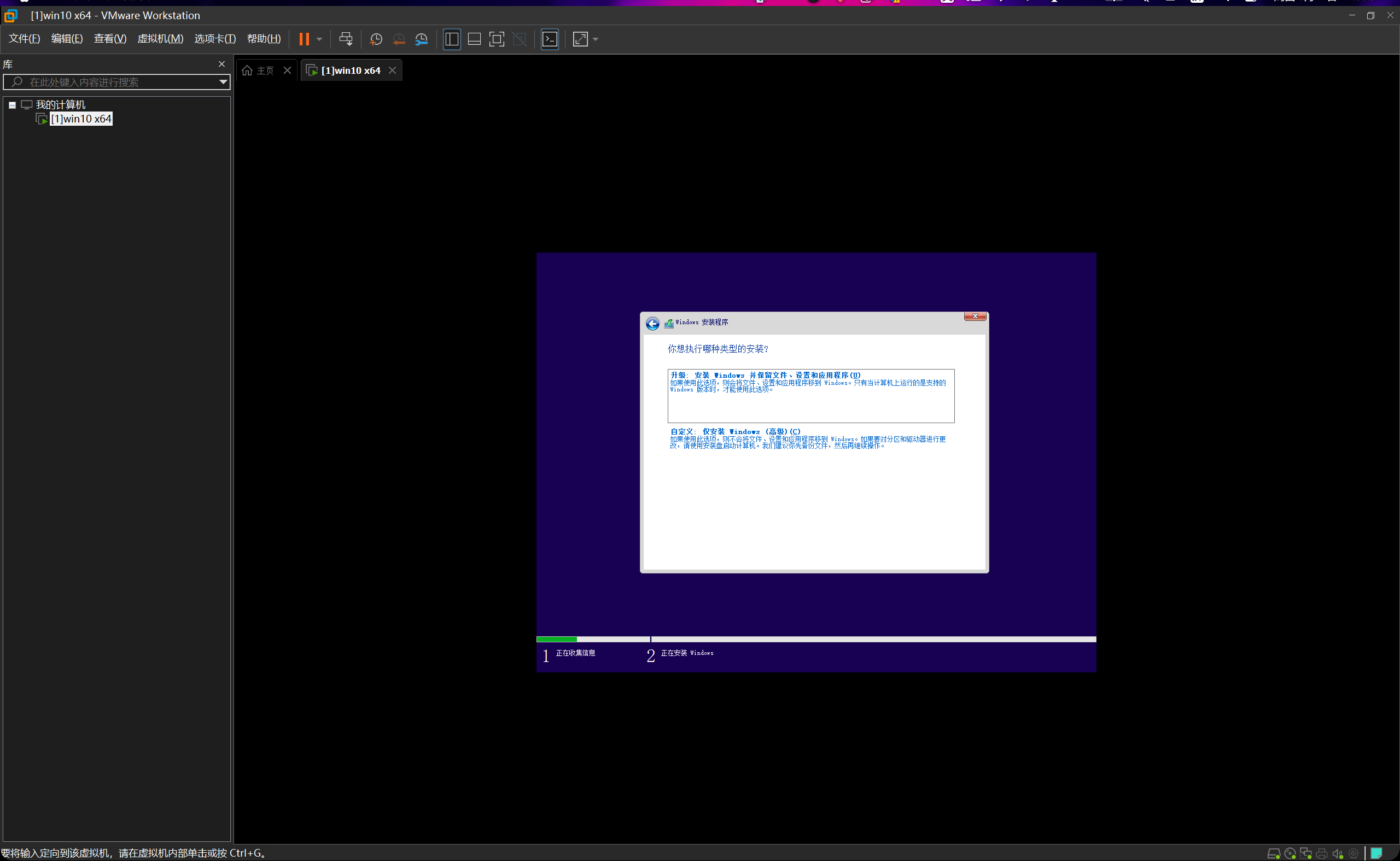
然后继续，选择这个磁盘。

安装ing...

好了

安装成功，同理我们可以安装好另一台虚拟机。

现在两台都已经安装完毕。均为Windows10 x64专业版，已激活。

检验连通性（尝试ping通）

首先要把两台虚拟机的防火墙全部关掉，否则ping不通。

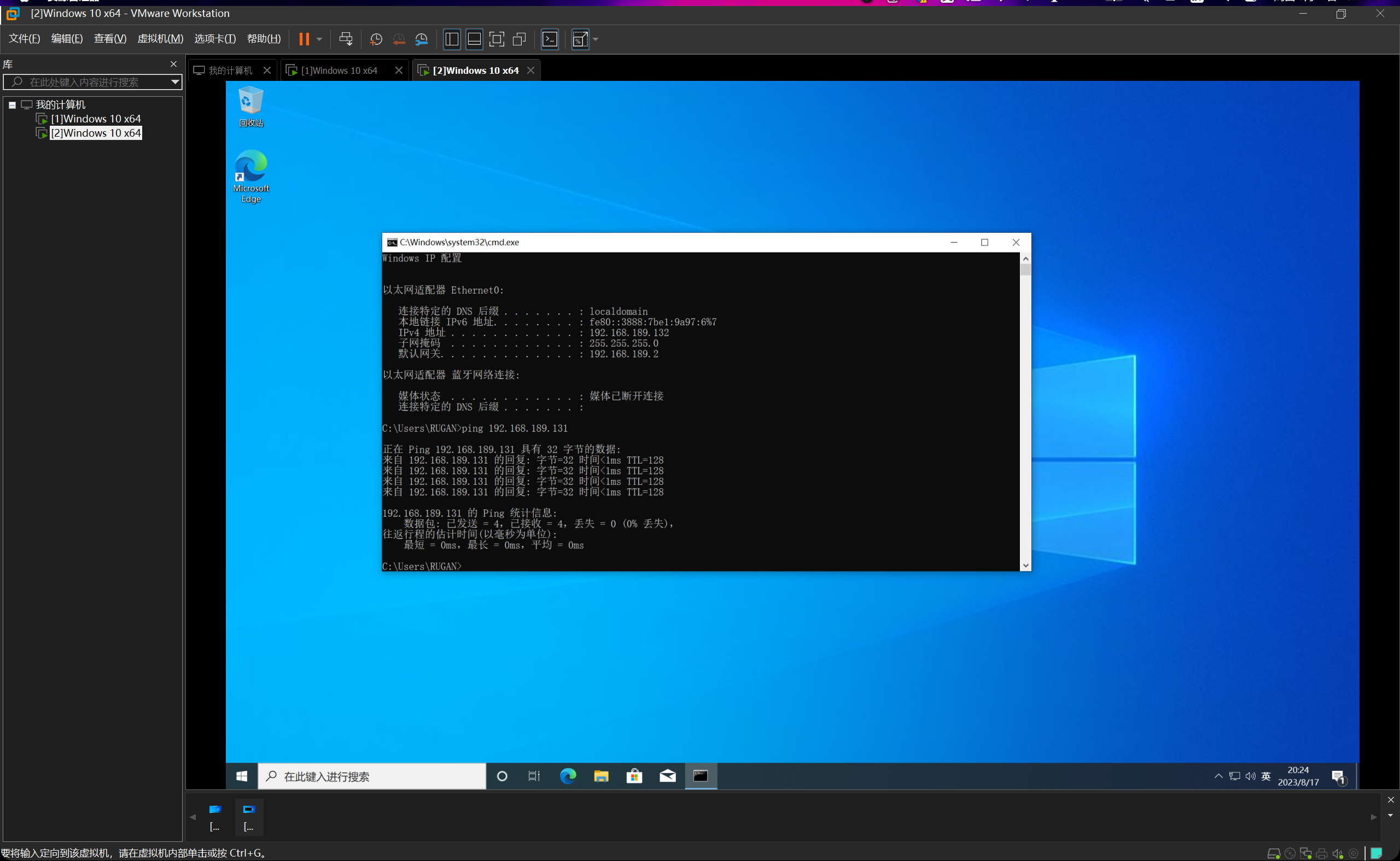
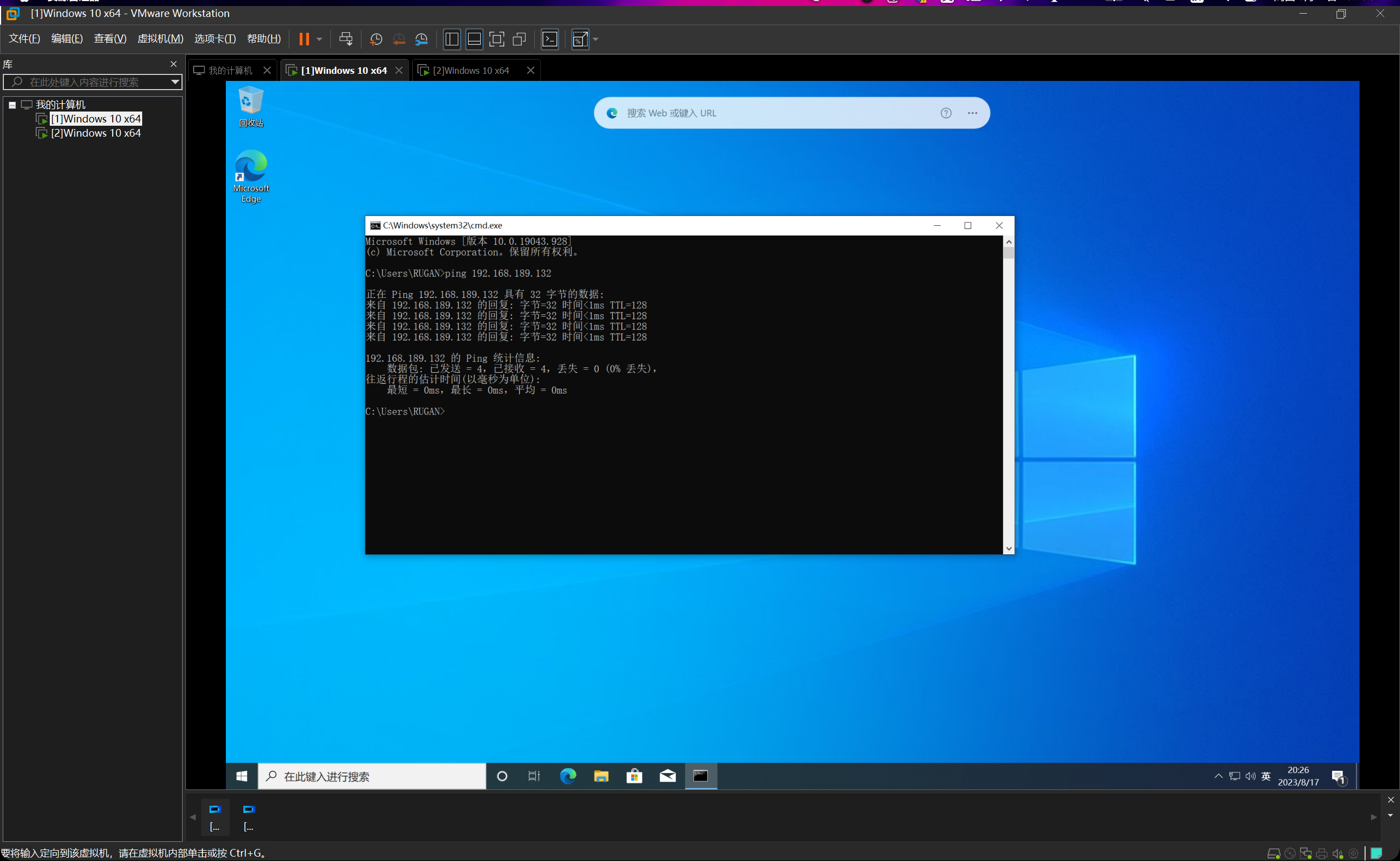
ok，两台均能互相ping通，连通性测试完毕。

安装相关环境

Python

直接到官网上下载即可。

选择所推荐的这个安装包。

下载安装即可。

记得添加到环境变量当中去，这样比较省事，后续就不需要自己再去搞了。

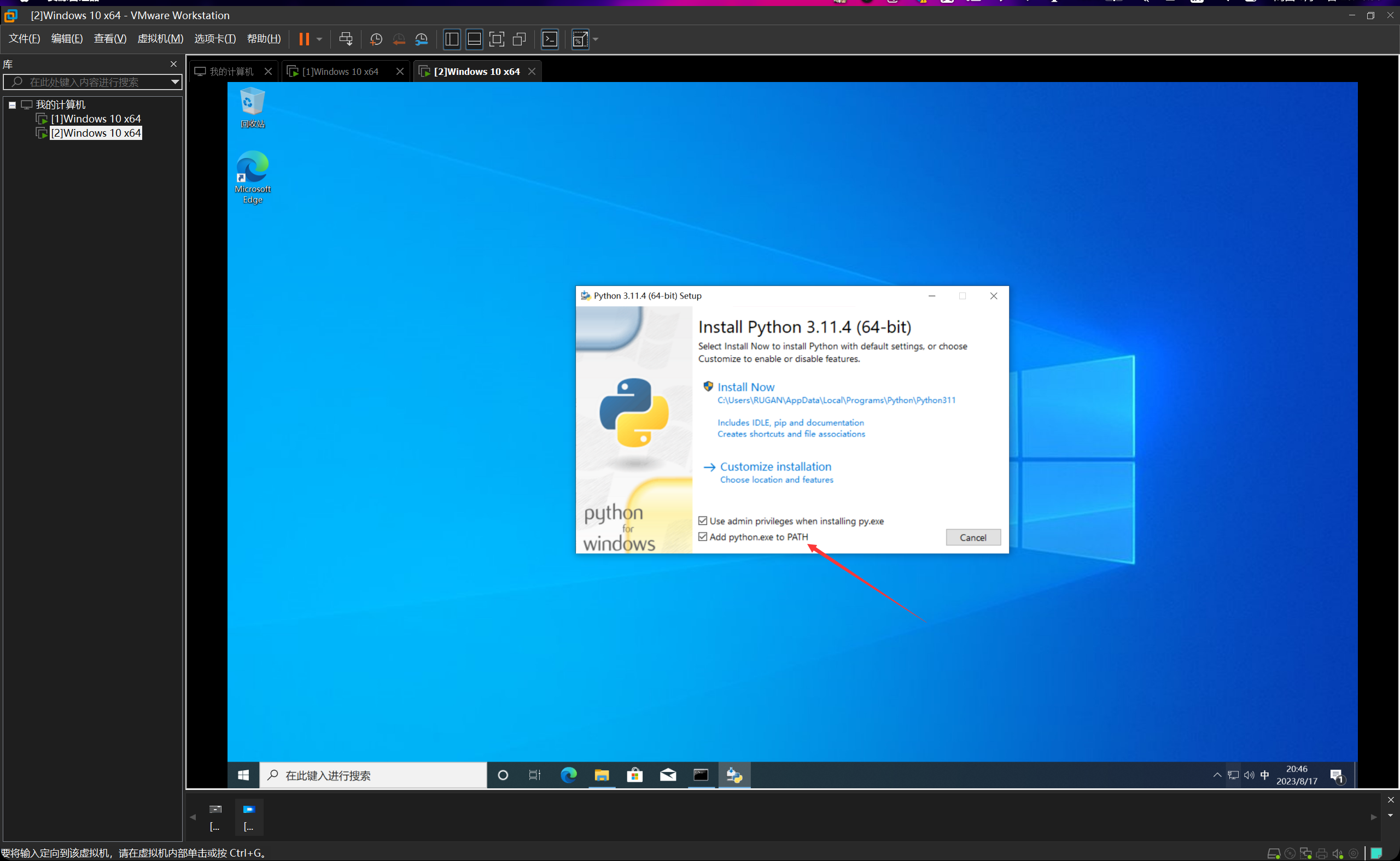
安装完成后，打开cmd，然后输入python并回车，如图所示，说明安装成功。

scapy

直接利用python的包管理工具下载即可，在cmd中输入指令pip install scapy回车即可开始安装。

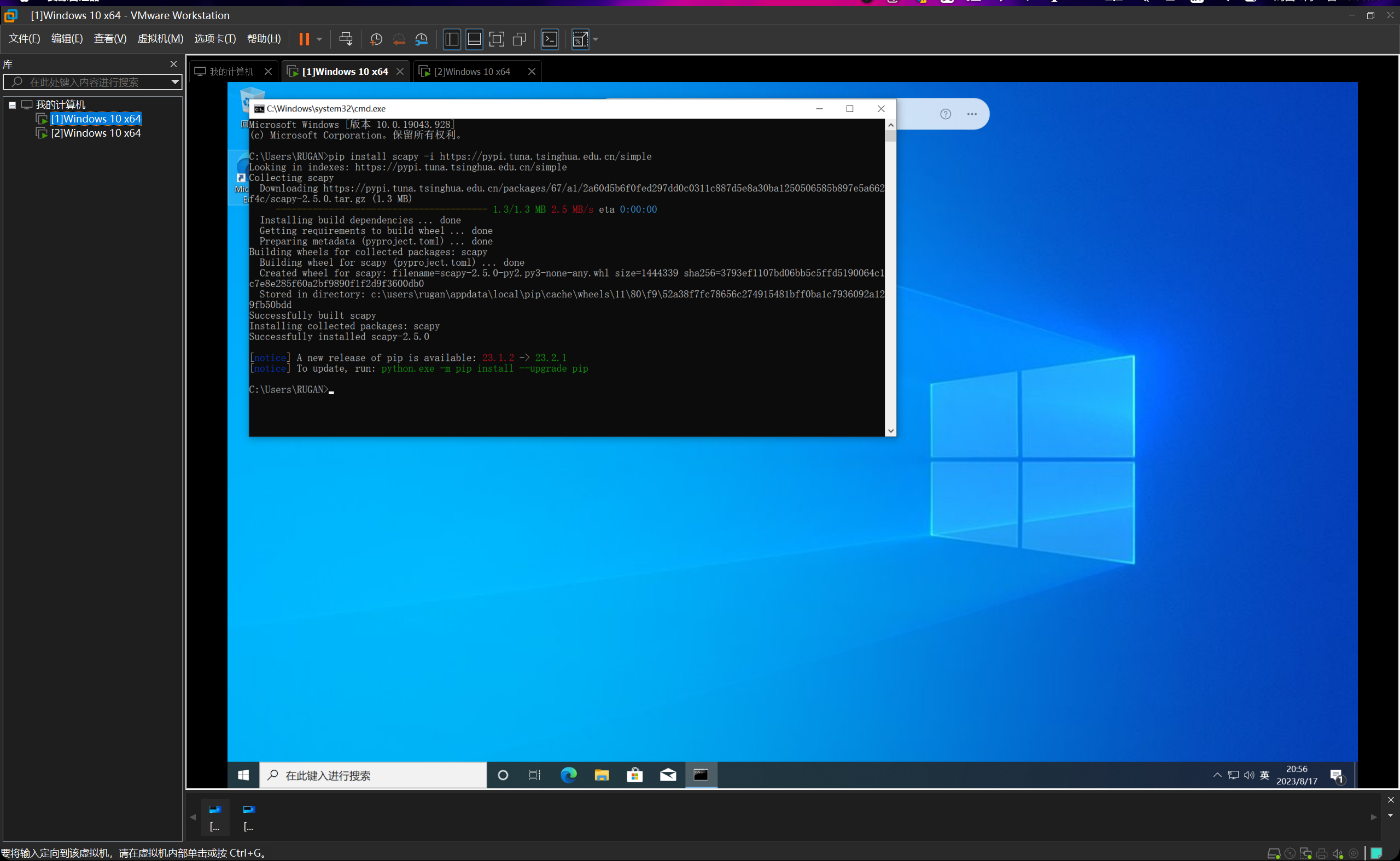
但是发现速度太慢了，直接用清华大学的镜像源下载吧。pip install scapy -i https://pypi.tuna.tsinghua.edu.cn/simple

三秒钟就安装好了。

可编程网络实验室2023暑期纳新——第二次作业

这个作业属于哪个课程	2023暑假作业
这个作业要求在哪里	可编程网络实验室2023暑期纳新——第二次作业
这个作业的目标	使用scapy实现数据包的发送，构造和接收，利用count-min sketch估计流频率，完成生活区答题

前置操作

由于我们需要对资源包进行捕获和嗅探，所以我们需要提前先安装好Winpcap或者Npcap，但是由于Winpcap已经被弃用，所以我们选择Npcap。直接在百度搜索Npcap，进入官网。

点击这个安装即可。如下图所示。

然后一直按下一步就好了。

安装好了之后，为了写代码方便，我们在两台虚拟机上都安装了Pycharm。然后这个Pycharm是可以用福大邮箱认证学生身份，来进行免费使用专业版软件的，这里不再赘述其方法。

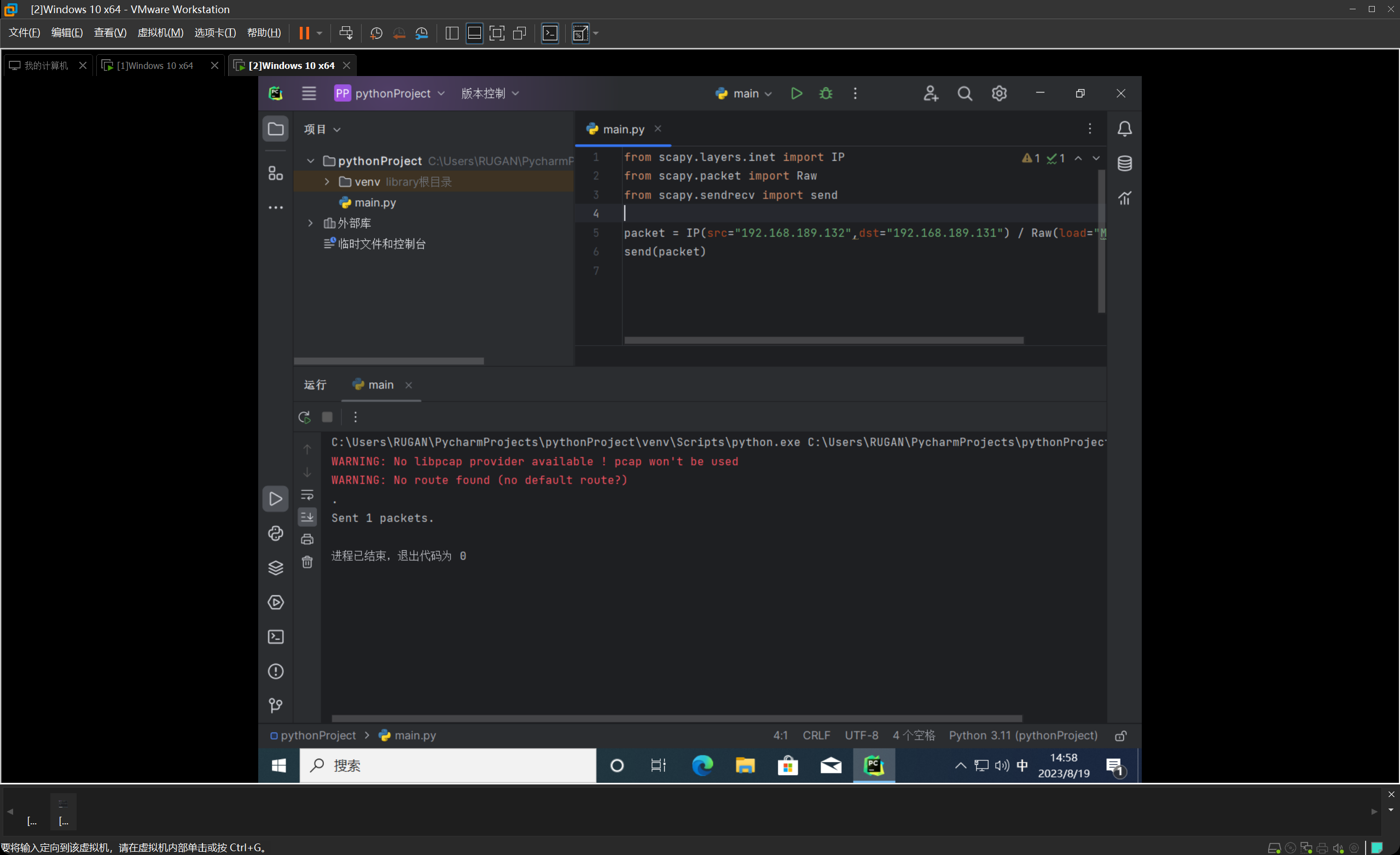
安装完之后，我们开始构造一个数据包，并尝试往另外一台虚拟机发包，我们把src和dst都写上，并指定Raw层的load为MEWWW，方便等一下收包解析确认。

我们在另外的那台虚拟机编写如下代码，进行数据包的嗅探。

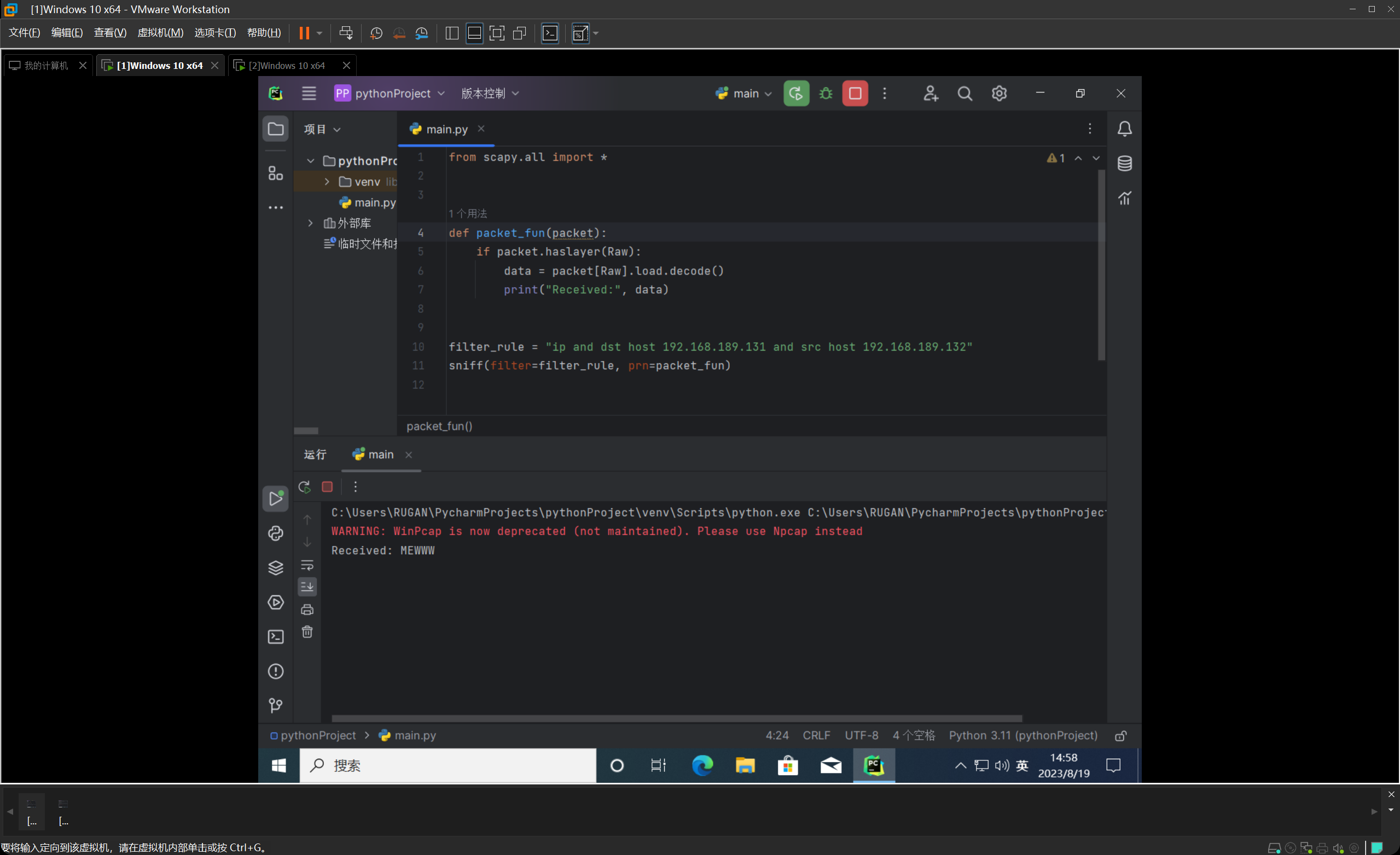
这里可能会发现警告，这是因为我一开始并没有装Npcap或装成了Winpcap。但是后来在编写后续代码的时候就索性把Winpcap卸了，换成Npcap了。下文图片可以看出。

然后我们发现很完美的可以正常的构造、发送、嗅探数据包了。

count-min sketch算法

算法介绍

• 当涉及到大规模数据流中的频率统计问题时，Count-Min Sketch（CMS）是一种用于近似计数的概率数据结构。它可以在有限的内存资源下，高效地估计数据流中元素的频率。Count-Min Sketch 是一个流式算法，特别适用于在实时数据流中进行频率统计。

• Count-Min Sketch 的主要思想是使用多个哈希函数将输入元素映射到不同的计数器上。每个计数器独立地维护特定哈希函数映射的元素的出现次数。通过在查询时将多个哈希函数的计数器值相加，可以得到一个近似的频率估计。

• Count-Min Sketch 有两个主要参数：宽度（width）和深度（depth）。宽度决定了每个哈希函数的计数器数量，而深度则决定使用的哈希函数数量。增加深度和宽度可以提高估计的准确性，但也会增加内存需求。

• Count-Min Sketch 主要用于解决频率统计问题，例如计算出现频率最高的元素、计算某个元素的频率等。但需要注意的是，Count-Min Sketch 提供的是近似估计，因此对于某些特殊情况可能会有一定的误差。

• 使用 Count-Min Sketch 的步骤如下：

  1.初始化 Count-Min Sketch，定义宽度和深度。

  2.针对输入数据流中的每个元素，使用多个哈希函数将其映射到对应的计数器，并将计数器值递增。

  3.在查询时，使用相同的哈希函数将查询元素映射到计数器，并返回多个计数器值的最小值。

• Count-Min Sketch 是一个用于近似频率统计的高效数据结构，适用于大规模数据流中的频率估计问题。它能够以较小的内存消耗提供近似的统计结果。然而，由于其近似性质，适用于某些特定的应用场景。

找到一张非常直观的图片

简而言之，相当于就是桶排计数这个思想升级到二维了而已。
对于每一套哈希函数，我们都能把一个序列的每一个元素映射到一个桶里去。（但是可能会由于哈希冲突导致桶被占用，导致我们的某个算出来的元素的频数会偏大），经过所有哈希函数的处理，我们就可以计算出根据不同的规则所统计出来的频数。但是由于哈希冲突的存在，所以的话，最后不同哈希函数计算出来的值，只可能是大于等于真实值。那么我们在所有哈希函数所生成的值之中取个min就好了。

前置操作

我们需要构造出很多的数据包，然后就可以形成很多的“流”，（我的理解是想象一张图，然后每个IP地址想象成一个点，然后源地址和终点地址这样的一个数据包就相当于这两个点的一条连线。然后线重叠的越多就代表流量越大）
然后由于IP地址最多有32位二进制数表示，差不多有42亿，因此如果我们直接用RandIP()这个方法来随机生成src来构造大量数据包的话，重复的概率太低了，所以就会出现绝大部分的数据包频数都是1。如下图所示：

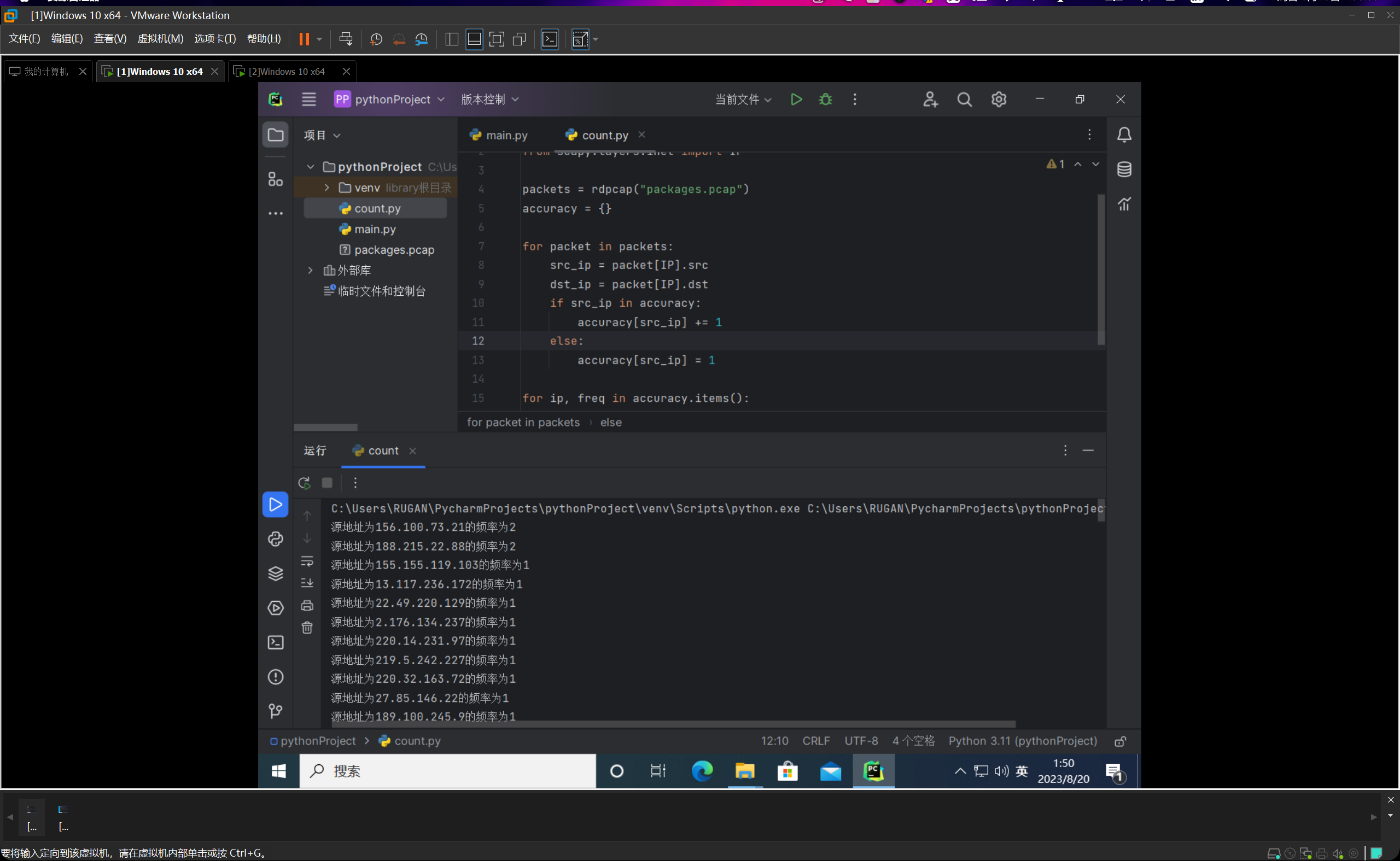
因此我换了一个方法。
我直接让IP地址的前三节写死为192.168.189，然后第四节采用0~255之间的随机数，这样子的话，如果我随机生成10000个数据包，可以计算出来期望频数为39.21≈39，然后这样的数值就比较的合理。

具体实现

我们把上面的代码稍加修改，如下图所示：

这个是发送端代码：

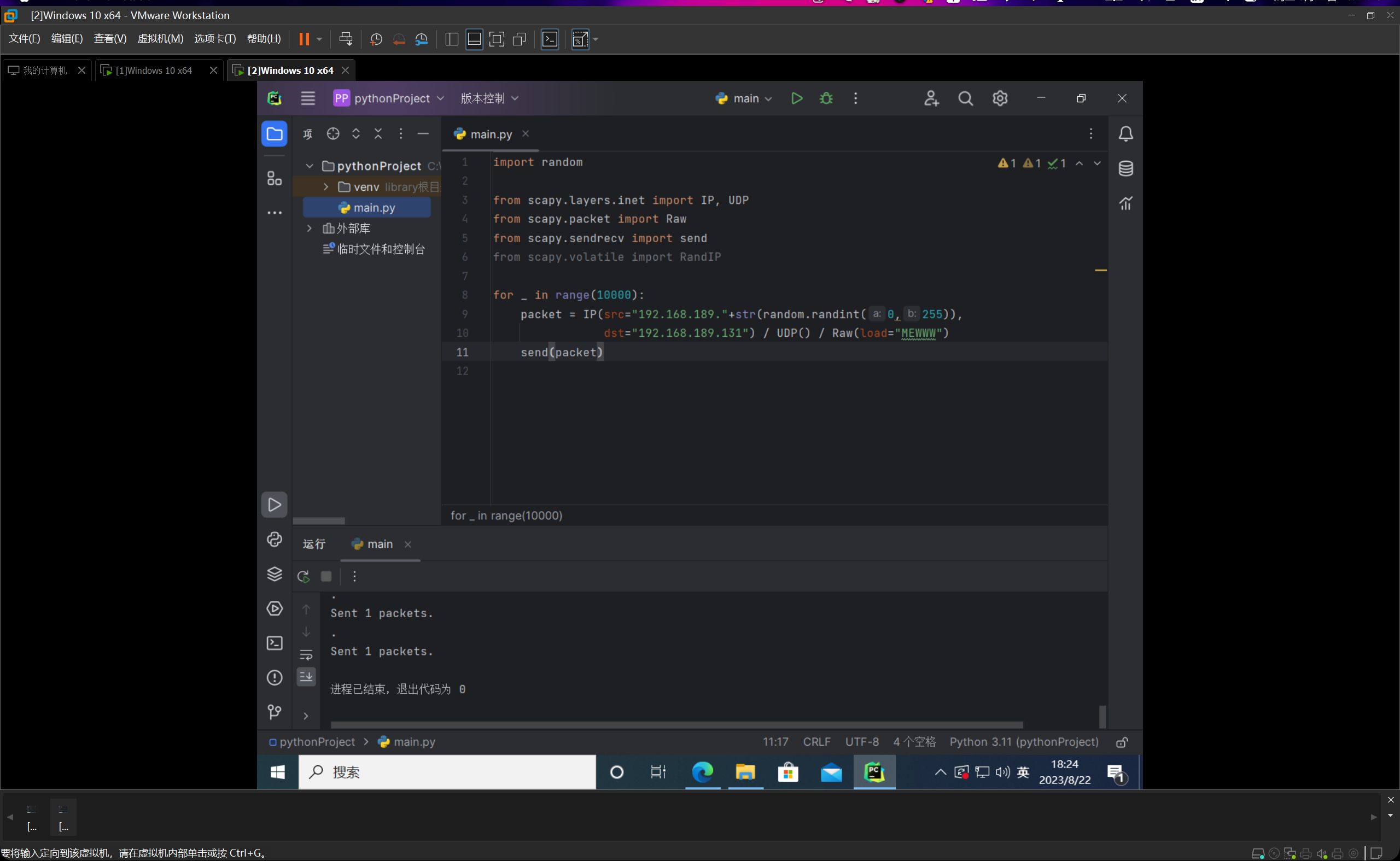
这个是接收端代码：

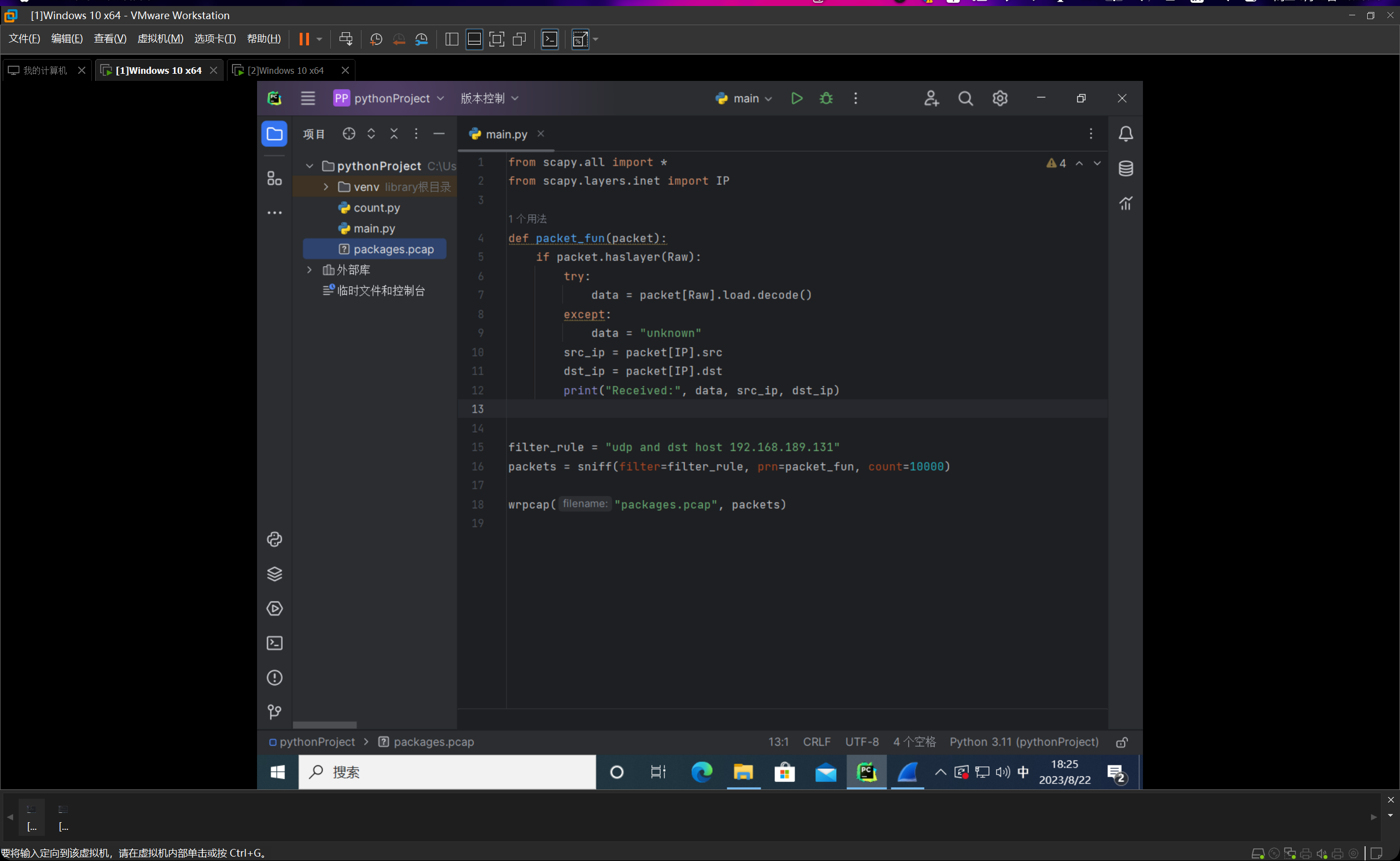
然后嗅探之后，我们为了方便后面的调试操作，就把这个数据包写入到本地文件里，我们命名为packages.pcap。运行完之后我们发现，项目文件夹里面多了一个数据包文件。

为了更直观，更全面，更清晰地查看数据包的内容，我们下载了小鲨鱼，也就是wireshark，这个可以百度搜索到官网下载安装，这里也不再赘述。

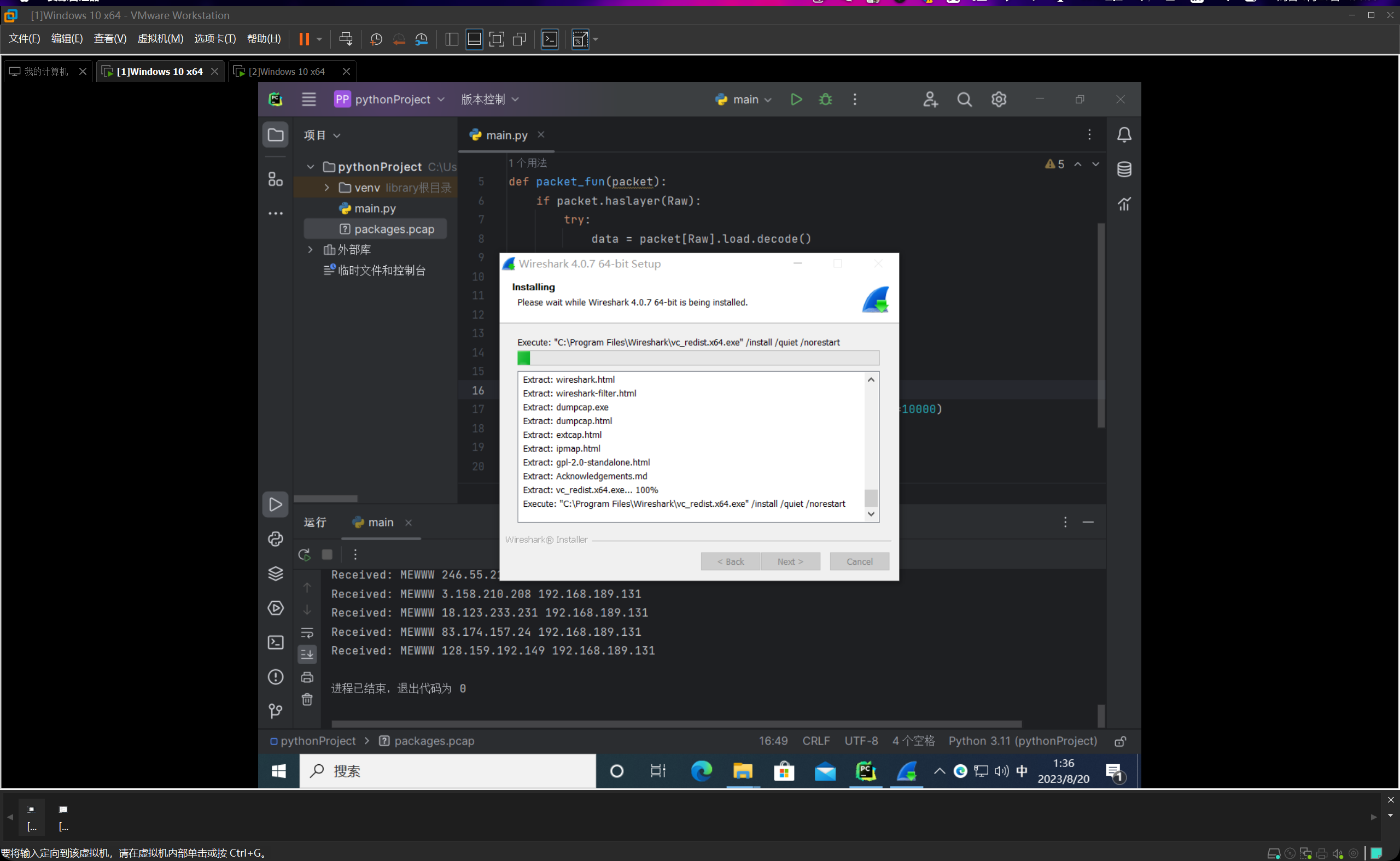
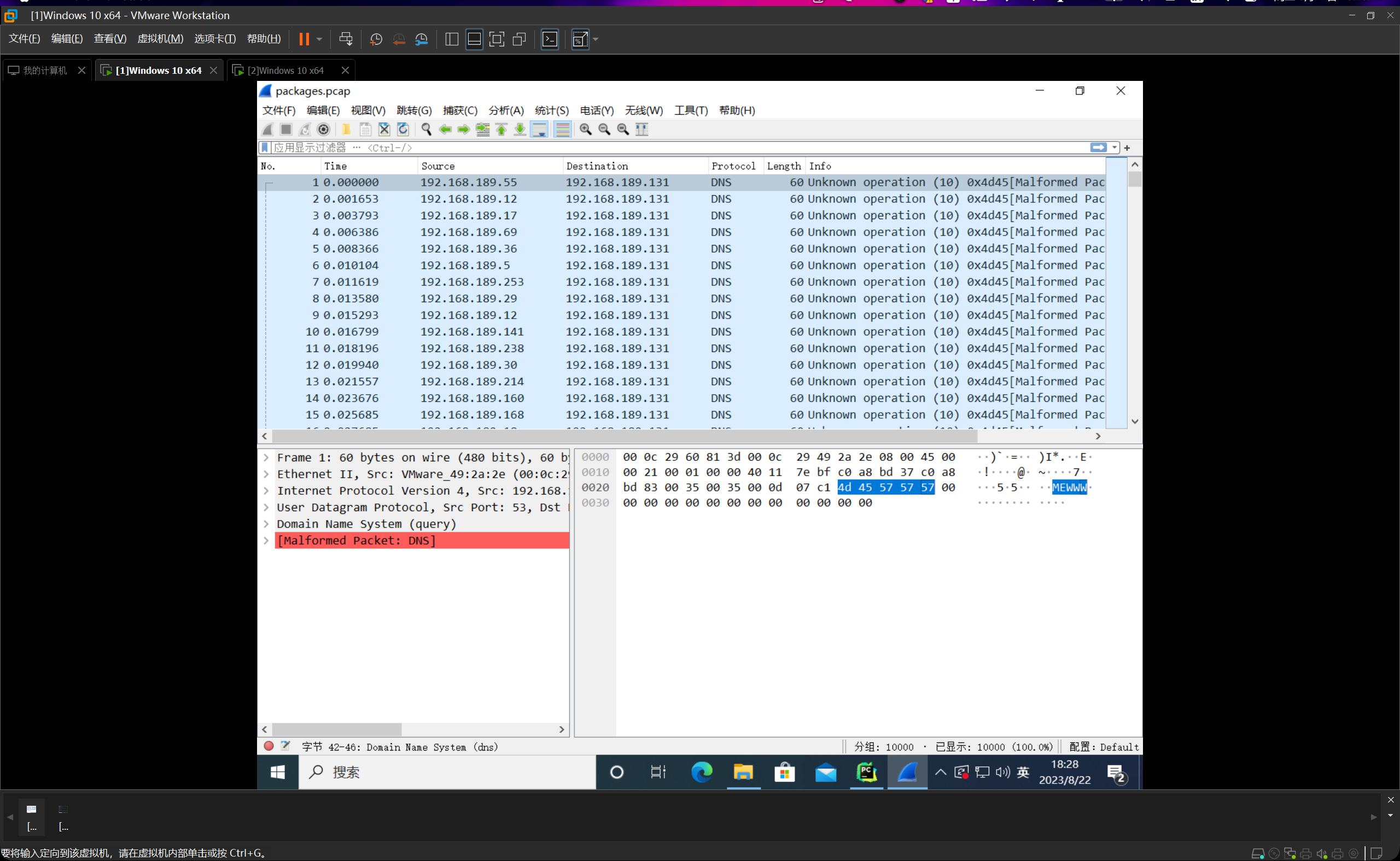
我们利用这个工具打开，如下图所示：

我们可以成功看到10000条数据包，并且都带上了load=MEWWW。这个数据包就为了等一下估计频数与误差分析使用。

我们编写count.py文件，如下图所示：

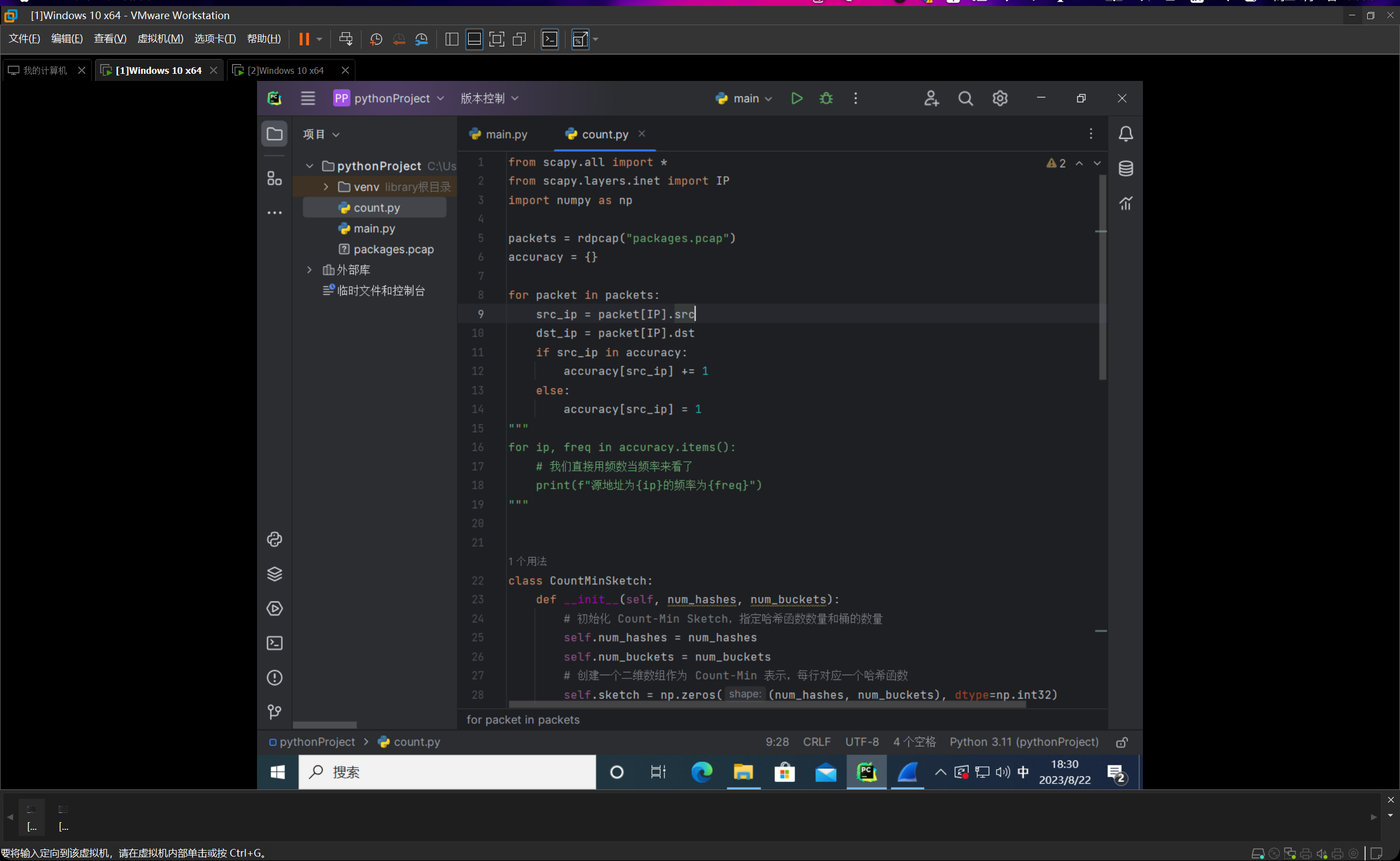
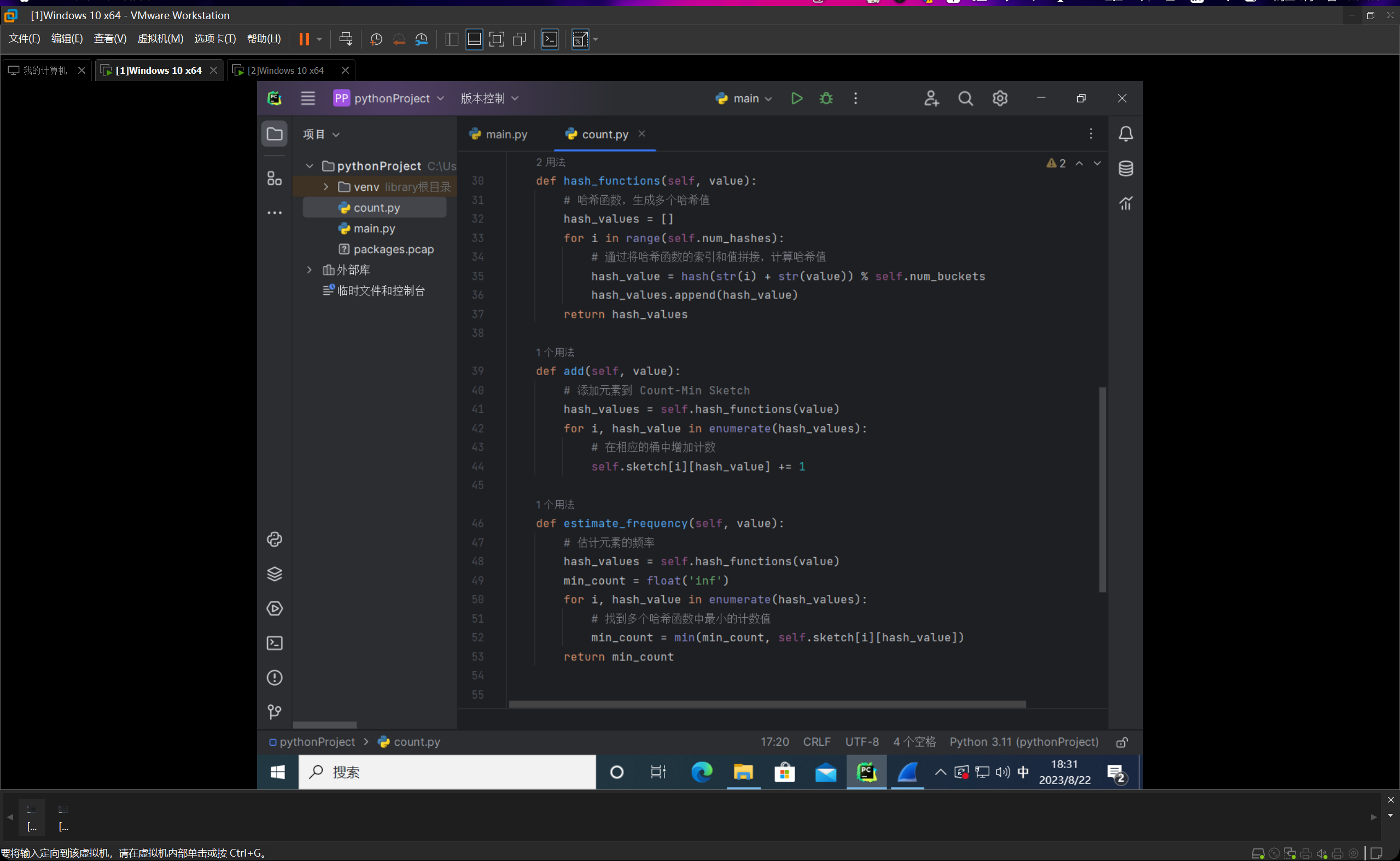
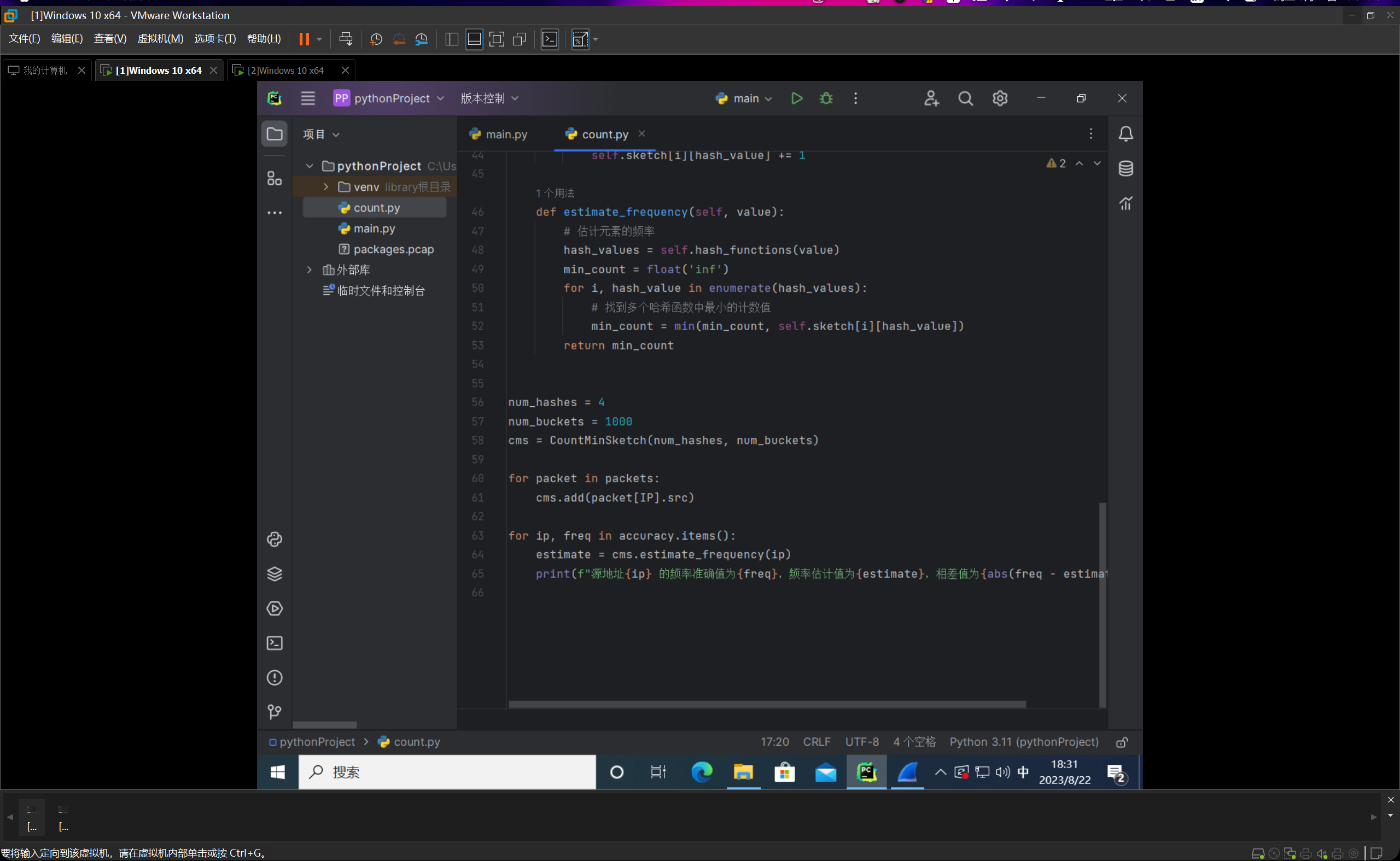
整个代码的思路就是我们先线性跑一遍，然后统计一下频数的真实值，然后编写完count-min sketch类后，进行计算与估计，然后输出的时候每条占一行，分别给出频率的真实值和估计值，并以他们的绝对值之差作为误差值。

这里会有不太准确的表述，我们这边计算出来的其实一直是频数，而不是频率，频率需要频数再除以样本总量数，再乘上100%，但是由于我们的期望频数就在39上下，所以的话呢如果这样进行转换的话会显得结果不太直观，但是其实道理都是一样的，我们这边直接约定把这里的频数叫做频率了。（其实最终数值也就差100倍，小数点移一下就好了一个意思）

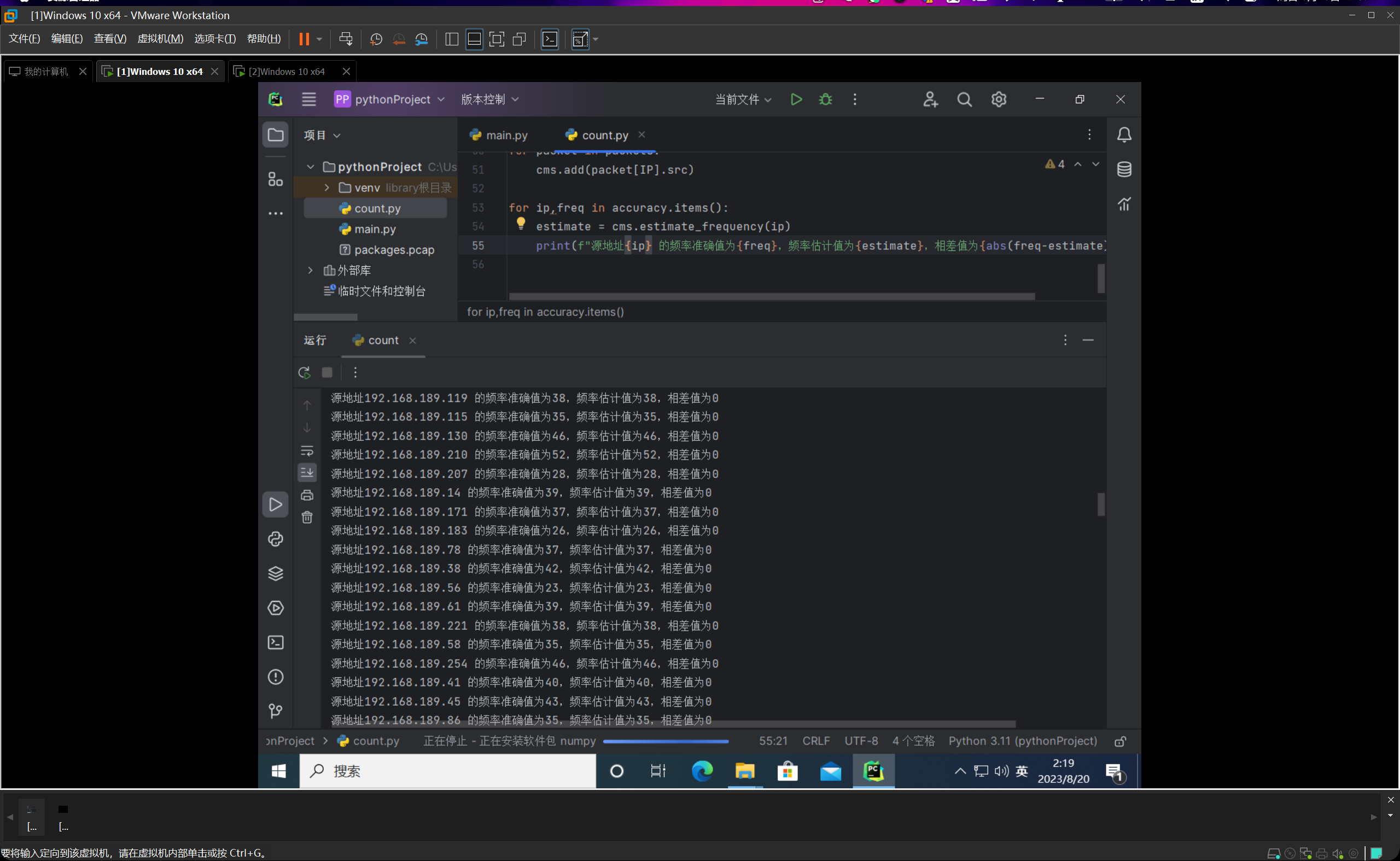
然后我们运行count.py函数，如下图所示：

我们把哈希函数的数量设置为4，然后桶的数量设置为1000，运行的结果十分惊人，10000个数据包，误差率为0，准确率高的离谱。由此也可见哈希函数为4，桶数量1000就已经可以达到非常精确的效果。我先后重新运行了几遍，误差率均为0%。

因此我就有了个想法，就是之后在实际的情况中，可以反复通过反复调整参数来达到时空效率和估计精度之间的一个平衡。因为毕竟过高的哈希函数和桶的数量都会导致时空代价增大。

但对这10000个数据包来说，哈希函数为4，桶数量1000一点压力没有，基本上可以在一秒之内计算出来，所以就没再考虑这个进一步的效率-损耗分析。

生活区问题

• 第一问：在人生道路上，你有没有专长的技能获取的成功经验？

我善于利用搜索引擎，网络上的博客，视频，官方文档，甚至于AI，再或者咨询他人。总之就是尽一切的信息获取渠道来帮助自己获取知识，解决问题。

• 第二问：你有什么技能比大多数人（70%以上）更好？

不畏困难，坚持不懈，刻苦坚毅的品格。我感觉这是最为核心和根源的吧。他给我带来了连续两学期单学期绩点第一，然后现在是西二在线工作室的前端组长，拥有项目合作经验和开发经历，比如说七月份的时候部署上线了一个二手游戏交易平台MewStore等等。还有就是数理思维？今年美赛拿了Finalist，数竞校赛拿了一等这些。感觉都是这种不服输的精神给我带来的附属品。

• 第三问：你是如何学习C语言的，与你的高超技能相比，C语言的学习有什么经验和教训？

因为我初一的时候就开始学习C语言了，所以C语言对我来说并不难，上学期也是轻松满绩。而对于学习的话，我感觉其实就是要细心，然后多思考，多试，多上机，遇到bug慢慢磨，一开始学习肯定会遇到各种麻烦或者很奇怪的bug，弄懂他并记住他，之后熟练了就不难了。

可编程网络实验室2023暑期纳新——第三次作业

这个作业属于哪个课程	2023暑假作业
这个作业要求在哪里	可编程网络实验室2023暑期纳新——第三次作业
这个作业的目标	高效测量判断heavy-hitters，解决Top-k问题，实现count-min sketch优化，信息压缩

准备数据集

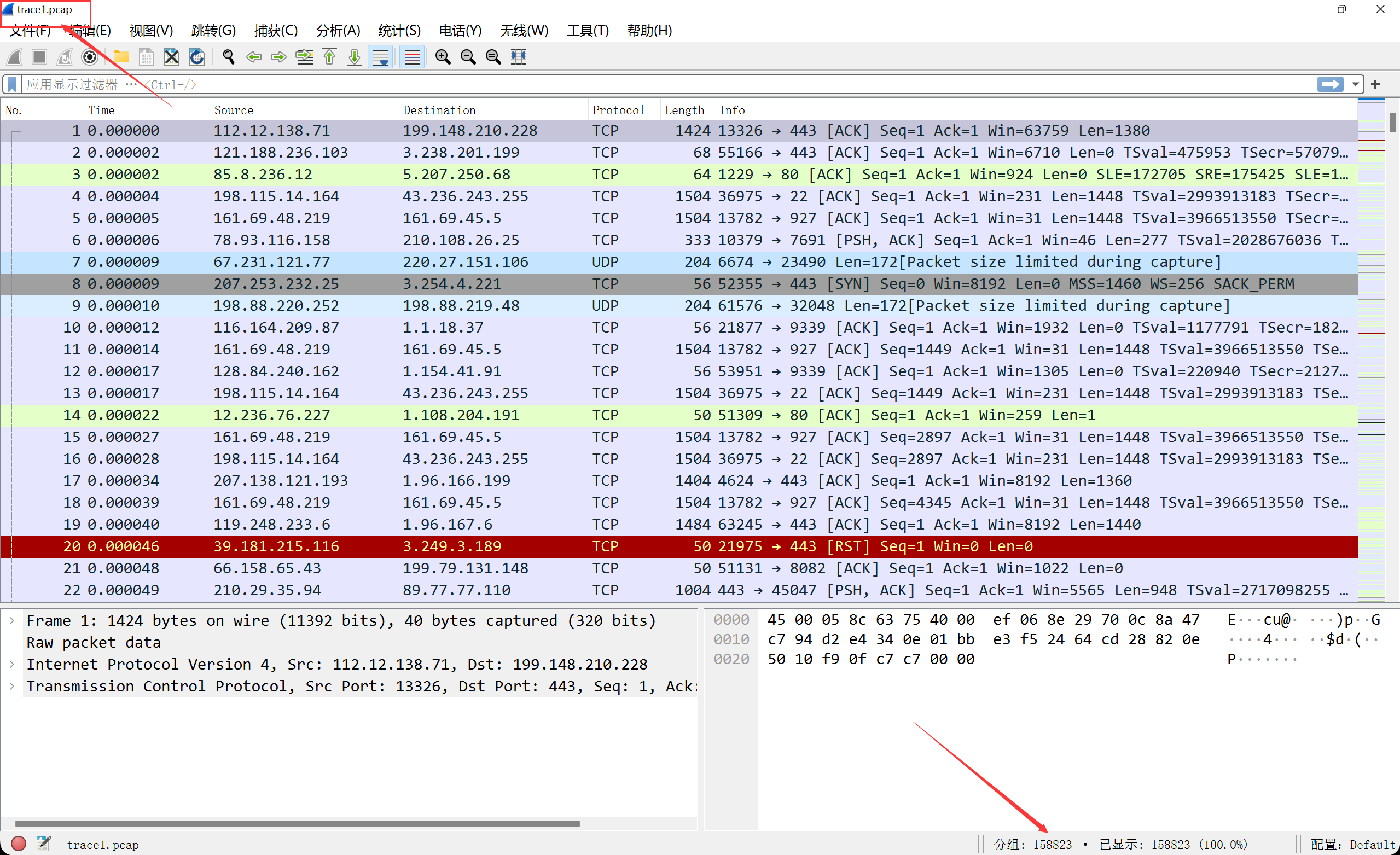
根据所给链接，我们可以定向到一个谷歌云盘，我们进行下载解压后，可以得到两个数据集文件。咱们用wireshark打开它，可以发现，两个数据包均有150000条左右的数据包。

这个是trace1.pcap这个包，一共有158823条数据包：

这个是trace2.pcap这个包，一共有159263条数据包：

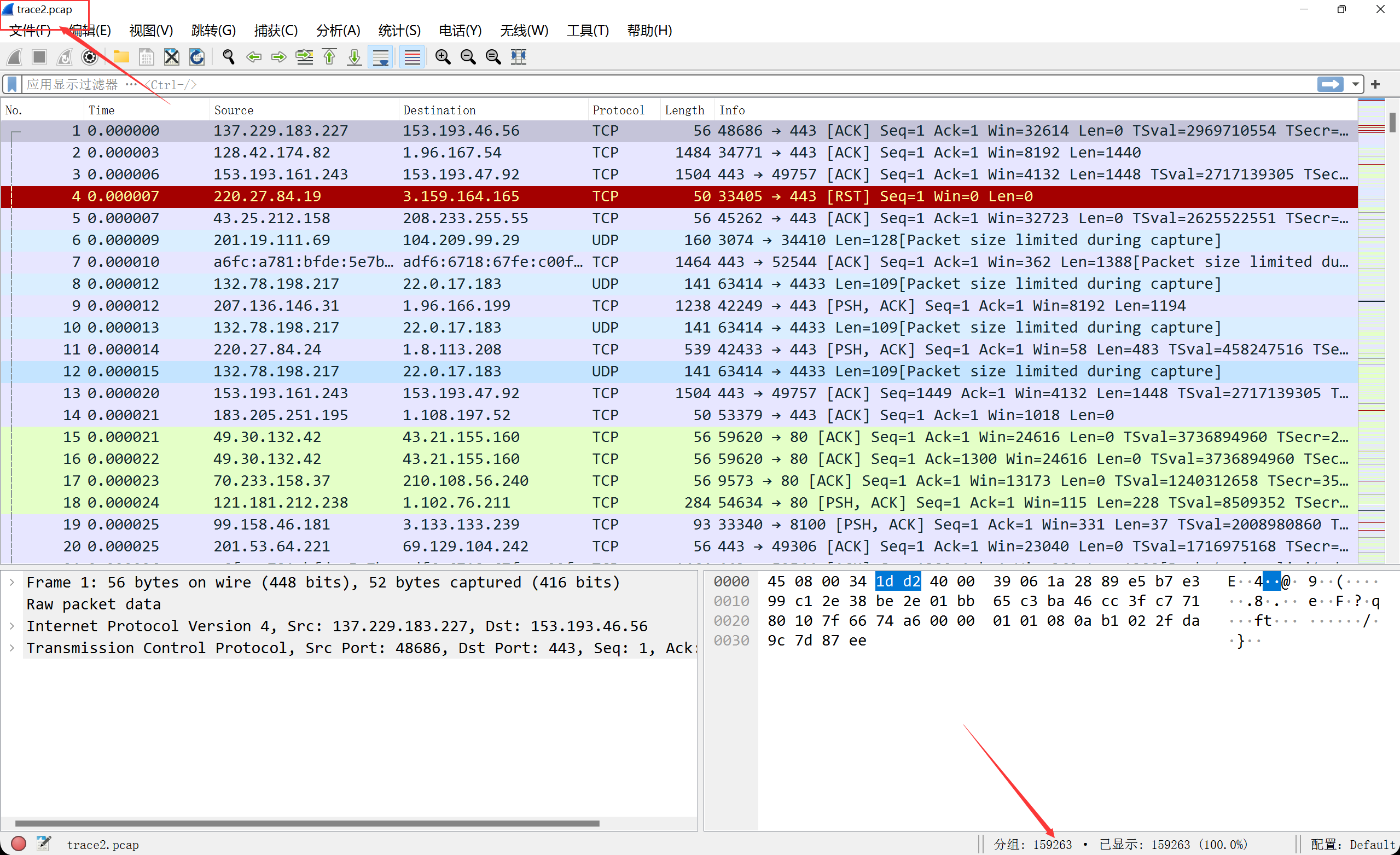
我们把这两个数据集移动到Pycharm的项目目录里，准备就绪。

随机抽样

因为我们的数据包的数量都在150000左右，光是读入就需要花个几秒时间，更不用说后续的运算操作了。而且，以后甚至可能有更庞大的数据集，因此进行完整的遍历运算肯定是不划算且是代价巨大的。因此我们首先先对数据集进行抽样操作。我们首先先抽样10000条，利用样本估计总体的思想，来进行后续的运算和估计。

python有对应的api，直接调用random库即可。

真实频率统计

为了用来检验后续的top-k算法的准确性，以及与样本的一个相对参考，我们把第二次作业的代码进行适当修改，计算出完整的数据集的真实频率和利用count-min sketch计算出来的估计频率。如下图所示：

然后，因为数据量太多，导致太开始的那些输出会丢失，无法在控制台中找到，因此我们对计算出来的数据进行升序排序，这样子最后输出的就是那些heavy-hitters。就不会导致数据丢失的问题。

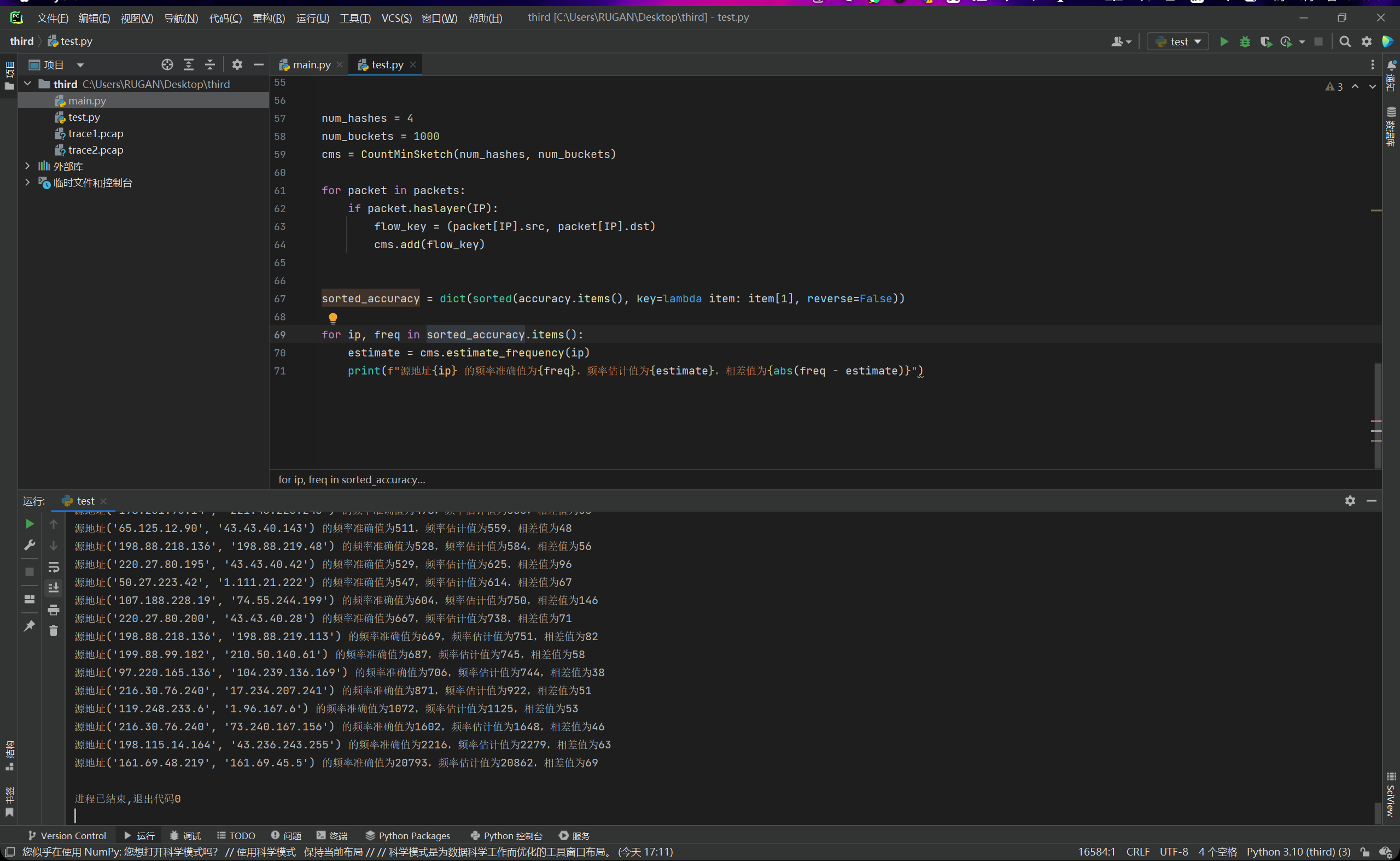
但是我们发现，当哈希函数数量为4，桶数量为1000时，我们的误差就变得非常的大了，毕竟我们这个时候的数据量已经达到了十五万，说明精度已经不够了。因此我们尝试把哈希函数数量和桶数量后面都补一个0，然后再次运行，查看结果，如下图所示：

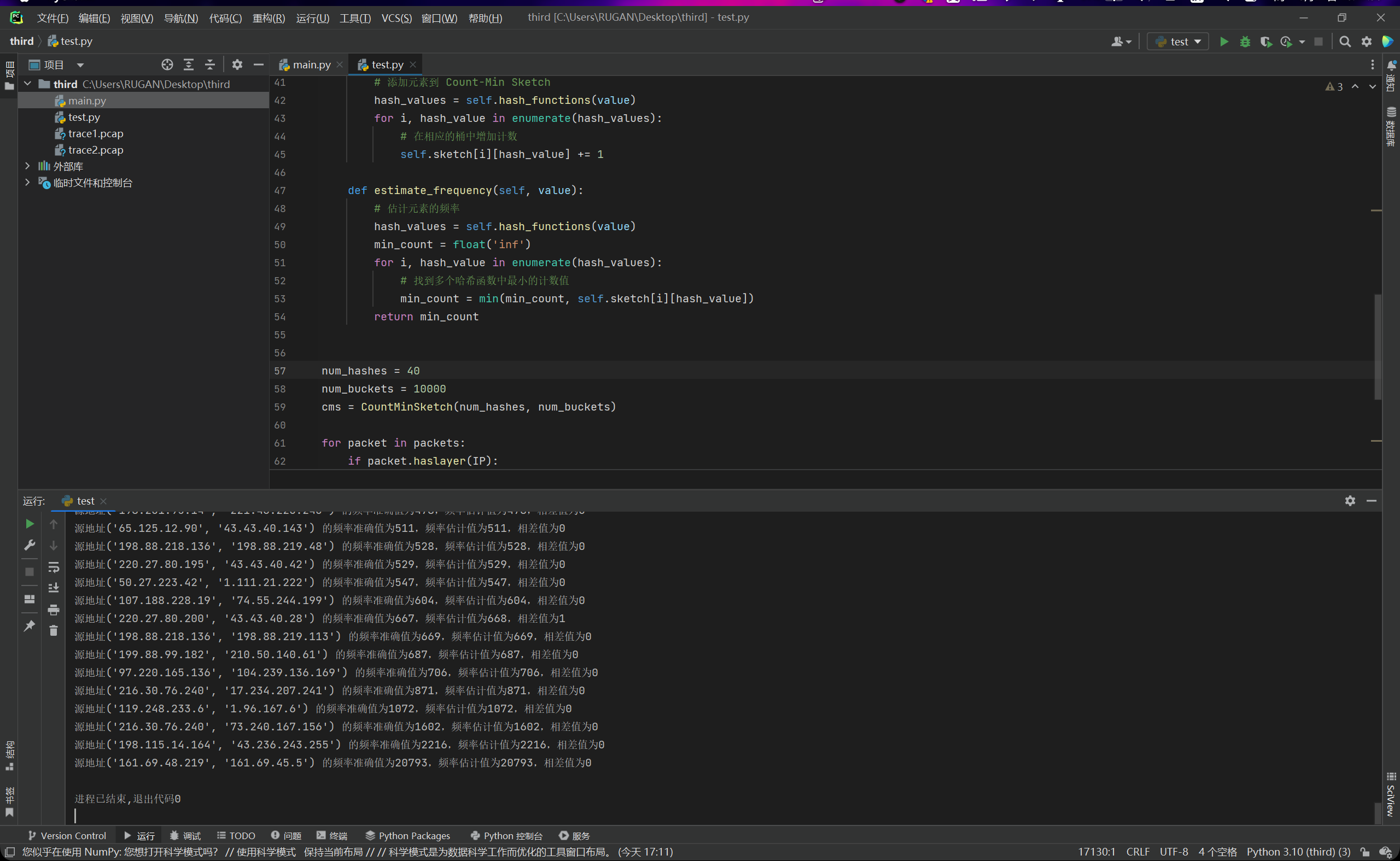
我们又回到了误差率为0的状态。那么这个时候我们对heavy-hitters们就有大致的概念了，大约是哪几条路线被“反复地走”，导致流量很大。这对我们后续计算出来的top-k可以起到一个验证的作用。

count-min heap算法

如果利用暴力方法，则每次都会对数据集进行一次遍历操作，则时间复杂度为\(O(kn)\)，对于我们跑完了的count-min sketch，我们可以维护一个大小为k的最小堆，然后就能把时间复杂度降到\(O(nlogk)\)

我们对原来的count-min sketch进行修改，另这个新类叫做count-min heap，如下图所示：

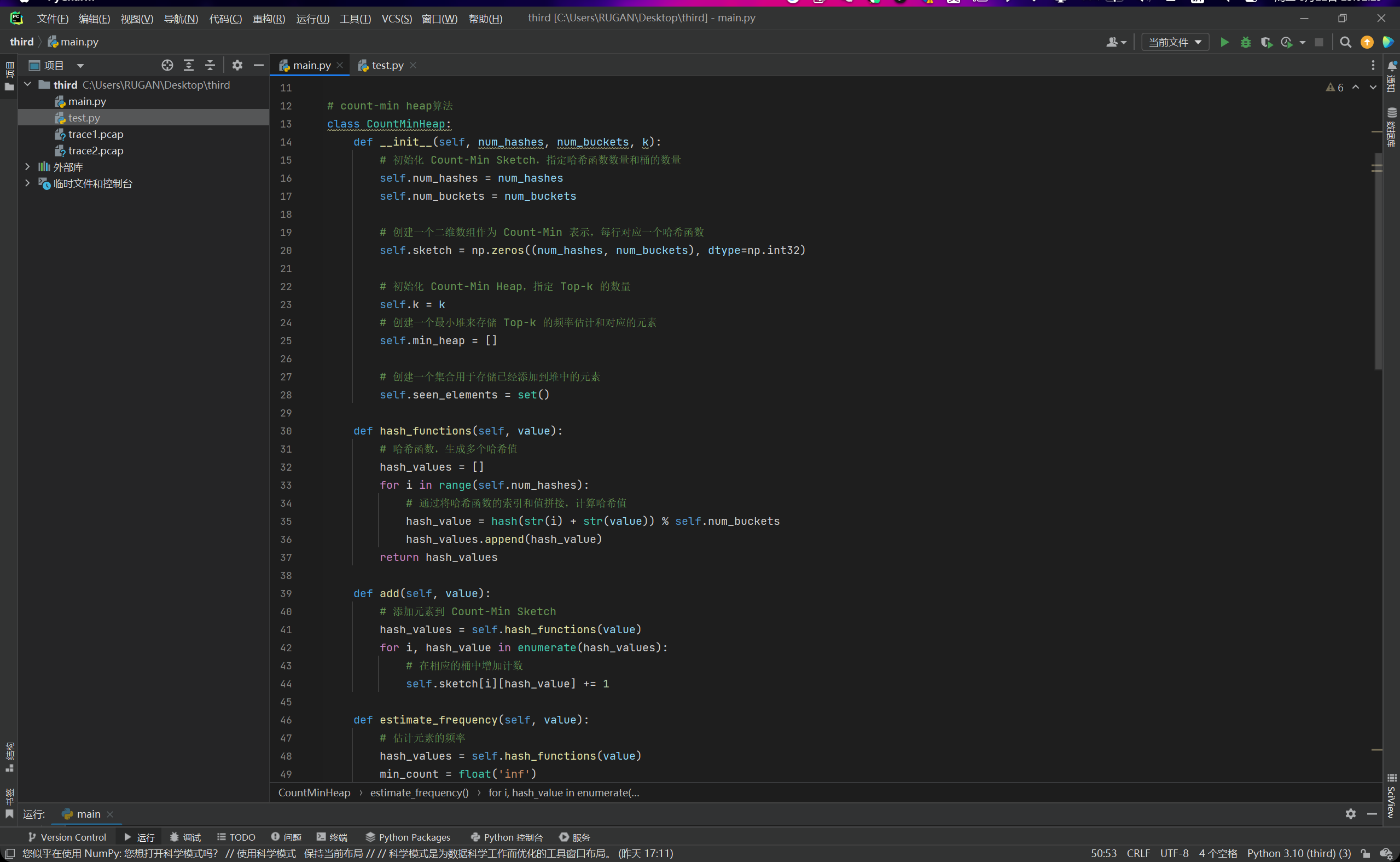
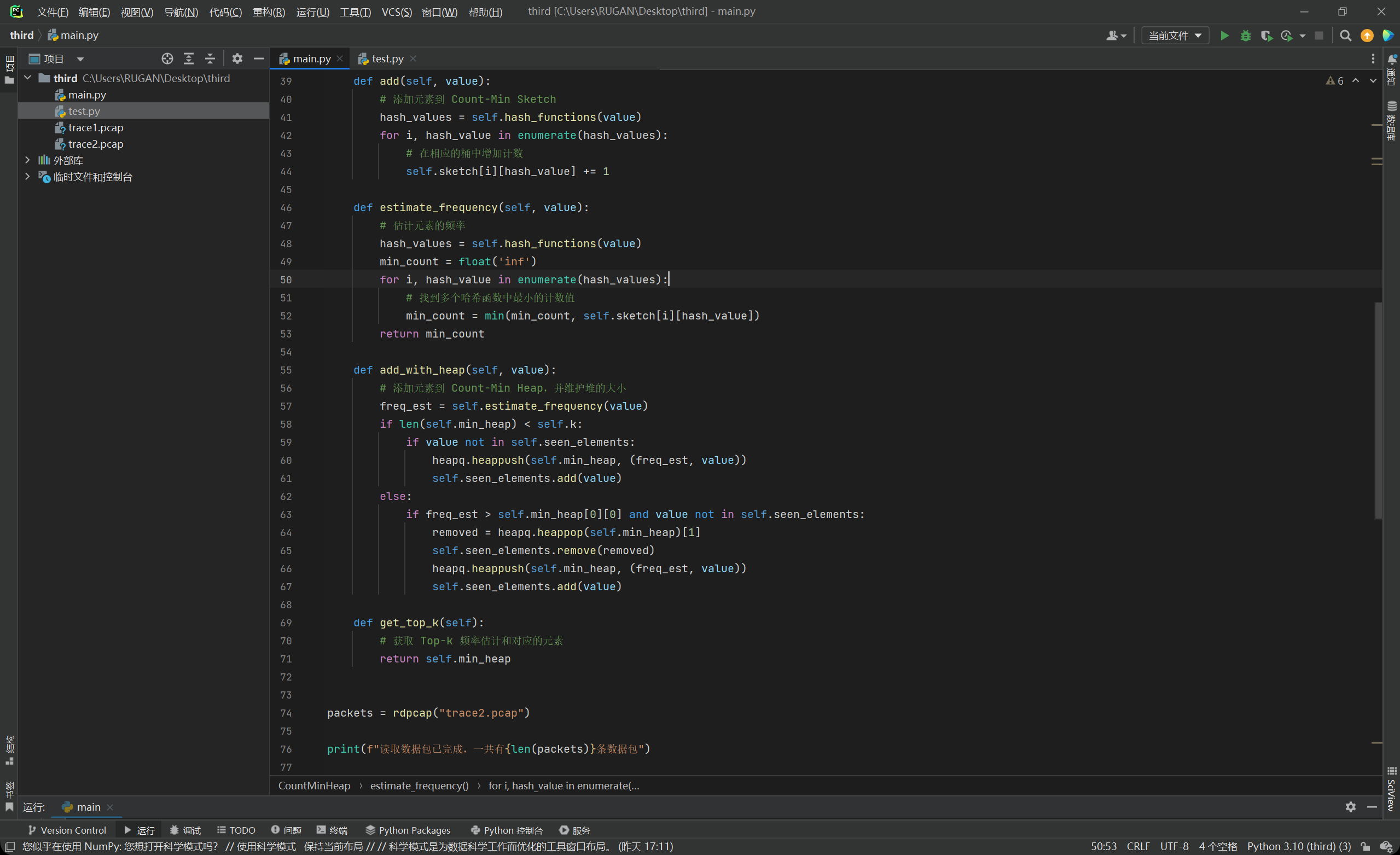
这样就可以提高时间效率。然后需要注意的是，最后生成的top-k这个堆不一定是有序的，所以的话最后还需要自行对他进行从大到小的排序。

运行，结果如下图所示：

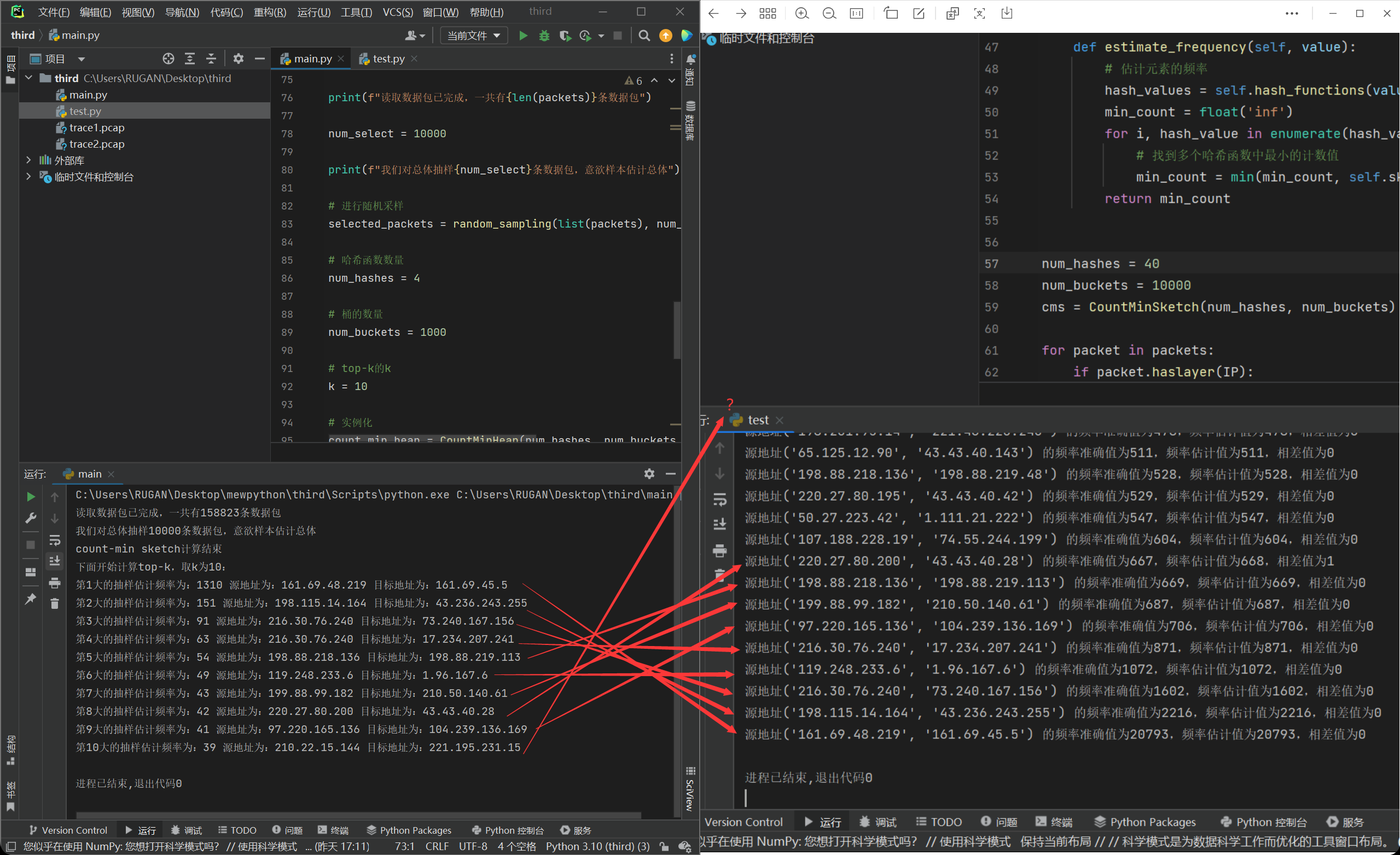
我们可以发现当样本大小为10000时，我们top-k排序出来的前四是吻合的，但是第五到第九的话顺序就会被打乱，但依旧是在前十条数据以内进行映射。不过top-k生成的第十条就已经误差很大了。我后来反复运行几次，也会发现这个问题，究其原因，是这个测量频率不够准确导致的。

我接下来从两个方面进行分析，锁定问题所在。

• 影响这个测量频率的因素有两个，一个是count-min sketch中的哈希函数数量和桶的数量不够大，导致的估计误差。
• 还有一个是样本数量太小，存在偶然性，导致并不能很客观地反应总体。

对于第一个方面，我在第二次作业中采用的就是哈希函数数量为4，桶数量为1000，这样的结果就是10000个包下来误差率为0%，因此这个估计计算误差基本上不是造成这个的问题。

那么就是第二个方面，15分之一的样本或许是真的太小，尤其是在准确的频数都已经非常接近的时候，这个情况就是难以避免的了，可能会相差一名两名。因此，处于尝试的目的，我把样本数量上调到了50000，运行程序：

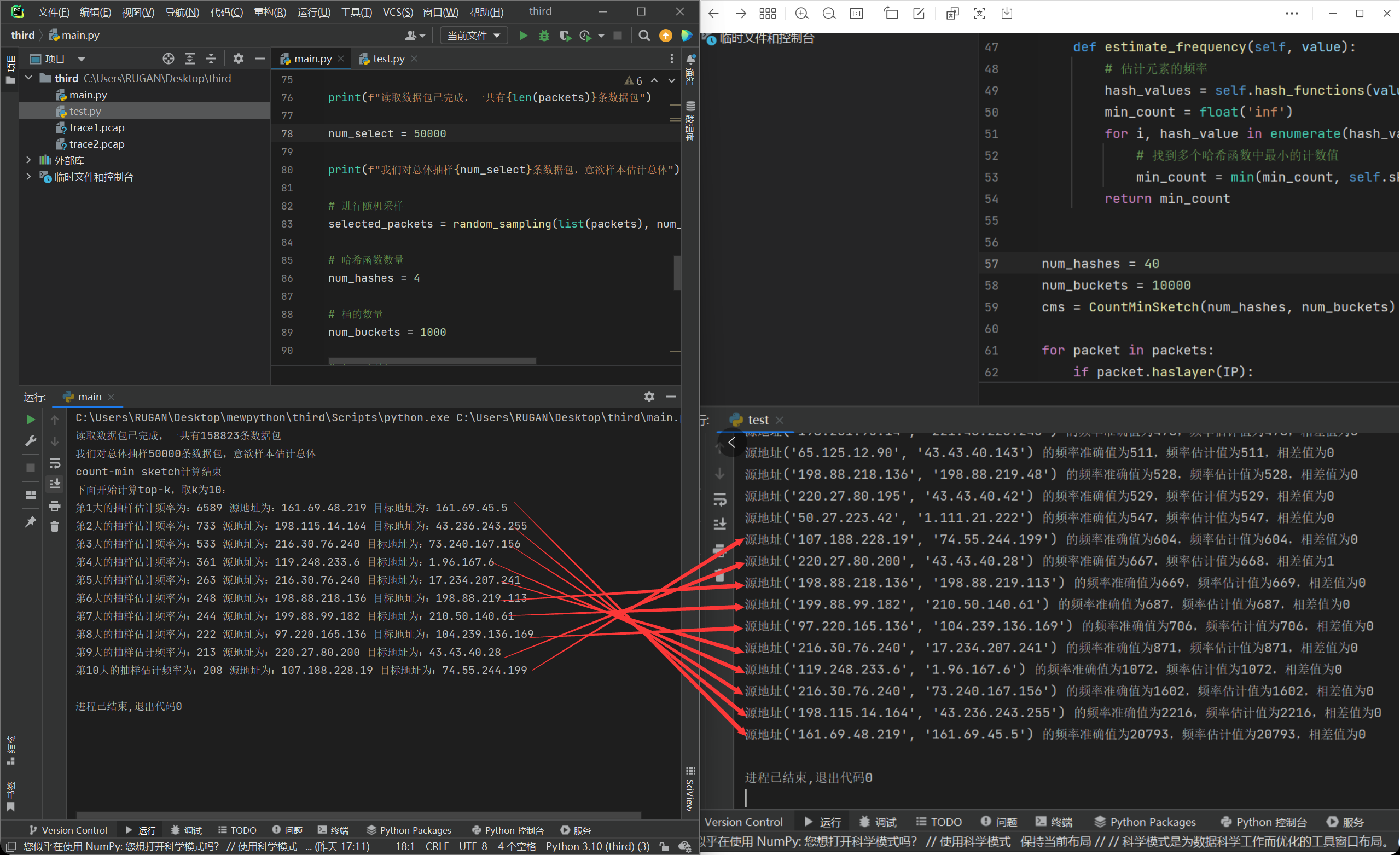
我们发现计算出来的结果有了很大的进步，但是依旧美中不足的是，顺序并没有完全对上。这个时候我们发现，我们这个时候样本数量已经是50000了，那么这个时候我们的哈希函数数量和桶数量说不定就不够了，导致第一类误差出现了，受此启发，我们试着把这两个参数进行上调：

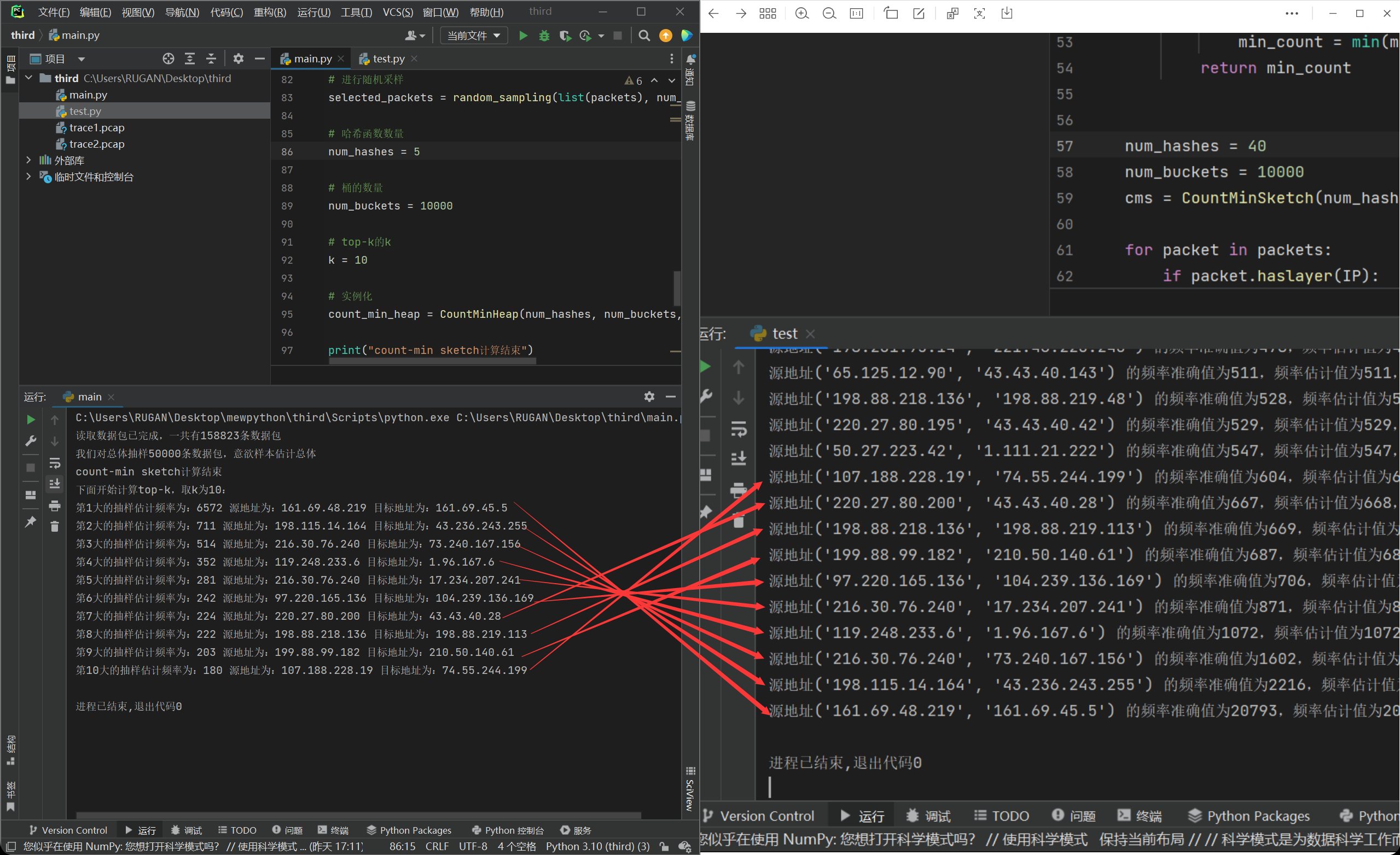
我们发现依旧是没有完全对上，但是这个时候的哈希函数和桶数量已经是足够高了，我也甚至调过100和50000的组合，依旧会出现这个情况。我们好好观察一下数据：

我们可以发现，出现平行线的那几条数据包，他们的真实频率都已经尤为相近，甚至只相差2，那就好说了。因为毕竟是抽样，所以肯定会有点精度缺失在的，而且更何况本来真实统计下，这几条的流量可以说是几乎一样了，我们看计算出来的频率估计值，也是十分贴近。因此如果要解决这个问题的话，把样本进行进一步的调大就可以了。

但是其实，解决top-k问题其实也就是要找出前k大的流，找到这些流既可了，并非一定要严格比较出高低和大小。因此我们这个时候也算圆满完成了top-k的求解。

因此，我们再对trace2.pcap这个数据集进行运算，我们可以得到结果如下：

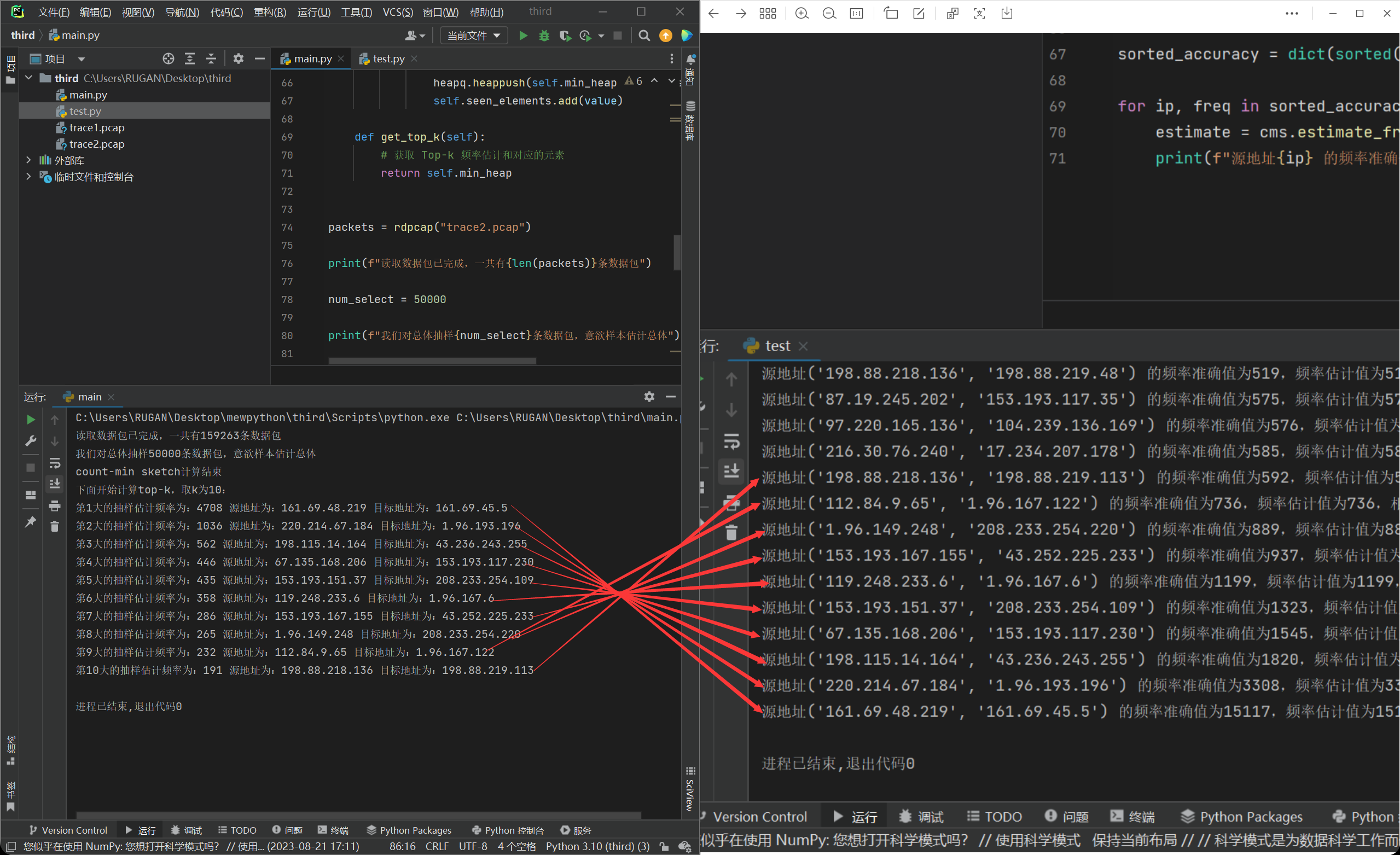
这个时候我们发现结果完全对上了，然后究其原因，是因为这个数据集没有那种很贴近的流量，因此就可以准确地分辨出顺序。更印证了我们的猜想。

压缩sketch

这里我考虑了很多种思路，包括什么差分编码、位图压缩，或者py自带的压缩算法。
但是，我们最后生成的top-k只包括估计频率，源地址和目标地址，然后我在生成top-k的时候，就已经采用了字典这种结构来存储源地址和目标地址，也就是把这个元组作为键，然后将频率作为值，这样子就已经是一种很紧凑的表示方法了。进一步的优化可能会受到数据本身的特点和压缩率的限制。因此的话其实把这个top-k进行上传也是无可厚非的。