结对项目作业

- GitHub 地址：https://github.com/senya-takasu/primaryMath
- 项目成员：黄杰，3117006581；黄常旺，3118005093；

psp流程估计时间

PSP2.1	Personal Software Process Stages	预估耗时（分钟）
Planning	计划	60
· Estimate	· 估计这个任务需要多少时间	60
Development	开发	2340
· Analysis	· 需求分析 (包括学习新技术)	420
· Design Spec	· 生成设计文档	240
· Design Review	· 设计复审 (和同事审核设计文档)	180
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	180
· Design	· 具体设计	600
· Coding	· 具体编码	240
· Code Review	· 代码复审	240
· Test	· 测试（自我测试，修改代码，提交修改）	240
Reporting	报告	540
· Test Report	· 测试报告	360
· Size Measurement	· 计算工作量	120
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60
合计		2940

题目
- 设计一个自动生成四则运算算术题的控制台程序，或者其他类似功能的程序。
  - 支持加减乘除算符，支持括号
  - 支持整数和分数，其中，当分数的分子的绝对值大于分母时，采用带分数形式，如11/4应显示为2`3/4；
  - 生成的题目中计算过程不能产生负数，也就是说算术表达式中如果存在形如e1− e2的子表达式，那么e1≥ e2。
  - 每道题目中出现的运算符个数不超过3个。
  - 程序一次运行生成的题目不能重复，即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目。例如，23 + 45 = 和45 + 23 = 是重复的题目，6 × 8 = 和8 × 6 = 也是重复的题目。3+(2+1)和1+2+3这两个题目是重复的，由于+是左结合的，1+2+3等价于(1+2)+3，也就是3+(1+2)，也就是3+(2+1)。但是1+2+3和3+2+1是不重复的两道题，因为1+2+3等价于(1+2)+3，而3+2+1等价于(3+2)+1，它们之间不能通过有限次交换变成同一个题目。
  - 在生成题目的同时，计算出所有题目的答案，并存入执行程序的当前目录下的Answers.txt文件。
  - 程序应能支持一万道题目的生成。
  - 程序支持对给定的题目文件和答案文件，判定答案中的对错并进行数量统计。
  - 统计结果输出到文件Grade.txt
解题思路
- 随机生成算式，为限制算式的难度，限制操作数数量在2-4之间，操作符应当比操作数少一个，操作符不包括括号。
- 括号的生成利用递归实现，限制最多做两次递归调用。
- 生成算式实际上主要是两个操作，一个是生成操作数，一个是生成运算符号。把括号的部分也当作操作数处理。因为括号里面是一个式子，实际上一对括号里面就是一个合法的式子。
- 计算式子的值，将式子按照波兰表达式进行分析，比如1*（3+2），则转换成3 2 + 1 5 *，代表先做3+2，得到数字5，再做1 * 5。其实这样的式子并不是递归结构的波兰表达式。只是借用这个思想实现计算。
- 计算结果时采用的解析方式可以提取算式的运算特征，里面包括按照算法得到的计算顺序、每次计算的算符和操作数。这些信息可以用于查重和判断数值是否在合理范围内。

设计与实现

因为需要实现分数形式的计算。需要设计一个分数类。并为其重载运算符使得分数对象可以当作一般的整数类型运算。
class fraction
{
private:
int nume; //分子
int decm; //分母

   	int divise(); //最大公约数 
   	 void fix();   
   public:		
   	//重载运算符
   	    fraction operator+(const fraction& right);
   	    fraction operator-(const fraction& right);
   	fraction operator*(const fraction& right);
       fraction operator/(const fraction& right);
   	void operator=(const int& a);
   	void operator=(const fraction& a);	
   	bool operator==(const fraction& right);
   	//获取对象的数值
   	double value(); //按浮点数输出分数的值
   	int getDecm();	//分子的值	
   	int getNume();	//分母的值
   	//格式化字符串
   	std::string toString();
   };

设计一个生成算式的函数和一个计算算式的函数。
因为对STL容器不够熟悉，利用模板编写的运算特征提取仍然存在诸多bug无法处理，故没有实现查重功能。

代码

算式生成的代码，利用string流实现整型数据到字符串的转换。经过分析，随机生成算式是一个交替生成操作数和运算符的过程。生成操作数时，判断是否递归生成括号，进入括号内部，仍然从操作数开始生成。
```

       int pm::rollexp(std::stringstream& exc, int limit, int opn, int inn, int mark)
            {
               int tag = 0; //0代表生成数字或者递归处理，1代表生成算符
           char lastch = '\0'; //最后生成的一个算符
           int number = -1;//最后产生的数字
           int con;//随机操作控制;
           while (1)
           {

           if (tag == 0) //产生数字，递归的表达式也是数字
           {
   	        con = rand() % 4;//产生操作
   	        if (0 == con && inn > 0 && lastch != '/' && lastch != '-') //0.25概率允许递归
   	        { //除号后面不允许递归；
   	        		con = (rand() % opn) + 1;
   			        opn -= con;
   		    	        --inn;
   			        exc << " ( ";
   			        rollexp(exc, limit, con, inn, 1);
   			        exc << " ) ";
      		         }
   		        else  //生成数字
   		        {
   		        if (lastch == '-') //被减数需小于之前的数
       		        {
   			        	number = rand() % limit;
   			        }
   			    else if (lastch == '/') //除数不为0
   			    {
   	    		    number = 1 + rand() % limit;
  		 		    }
   			    else //正常生成0-limit的数字
   			    {
   				    number = rand() % (1 + limit);
   			    }
   			    exc << number;
   			    --opn;
   		    }
   		    tag = 1;//互锁结构的模式切换
   	    }
   	    else if (tag == 1)
   	    {
   		    con = (rand()) % 4;//产生操作
   		    if (0 == con)
   			    lastch = '+';
   		    else if (1 == con && 0 == mark)
   			    lastch = '-';
   		    else if (3 == con && lastch != '-' && lastch != '/' && lastch != '*')
   			    lastch = '*';
   		    else if (2 == con && 0 == mark && lastch != '/')
   			    lastch = '/';
   		    else lastch = '+';
   		    exc << ' ' << lastch << ' ';
   	    tag = 0;//互锁结构的模式切换
   	    }
   	    if (opn == 0) break;// end while check
       }
        return 1;
    }

利用波兰表达式的思路计算结果,由于没有统一使用容器，结构比较混乱，放出主循环结构介绍计算方法，最后一次运算的结果就是算式的结果。

  for (i = 0; i < size; ++i)
  {
  	ch = exp[i];//读字符
  	if (ch == '(')//左括号无条件进入操作符的栈
  	{
  		clist[itc] = ch;
  		++itc;
  	}
  	else if (ch >= '0' && ch <= '9')//检测到数字，则将数字拼接，然后放入操作数栈
  	{
  		for (num = 0; exp[i] >= '0' && exp[i] <= '9' && i < size; ++i)
  		{
  			ch = exp[i];
  			num *= 10;
  			num += ch - '0';
  		}lastnum = num; //拼接完毕后将数值交给分数类
  		flist.push_back(lastnum); ++itf;//指向栈顶下一个位
  	}
  	else if (ch == '+' || ch == '-')//检测到运算符+ -
  	{
  		while (1)
  		{//操作数栈空，或者栈顶为左括号，则直接入栈
  			if (itc < 1) break;
  			else
  			{
  				lastch = clist[itc - 1];
  				if (lastch == '(') break;
  				else //如果不比栈顶算符的优先级高，则弹栈运算
  				{
                      //弹1次符号栈，弹2次操作数栈。
                      //计算并将计算结果压入操作数栈
  				}//再次与栈顶比较直到可以入栈
  			}
  		}clist[itc] = ch; ++itc;//离开入栈判断循环再执行入栈操作
  	}
  	else if (ch == '*' || ch == '/')//检测到运算符 * /
  	{
  		while (1)
          {
              //同理+ - 运算符，因为* /优先级高于 + -
              //故多一条，栈顶为+ -时可直接入栈
          }//离开入栈判断循环再执行入栈操作
  	}
  	else if (ch == ')')
  	{
  		while (itc > 0 && clist[itc - 1] != '(')
  		{
  			//直到栈顶元素为左括号
              //执行弹栈运算（同理+ - * /部分的代码）
              //并将运算结果入栈
  		}//栈未空且栈顶为左括号，则再执行一次弹栈。
  	}
  	else;//空字符抛弃   
  }

效能分析
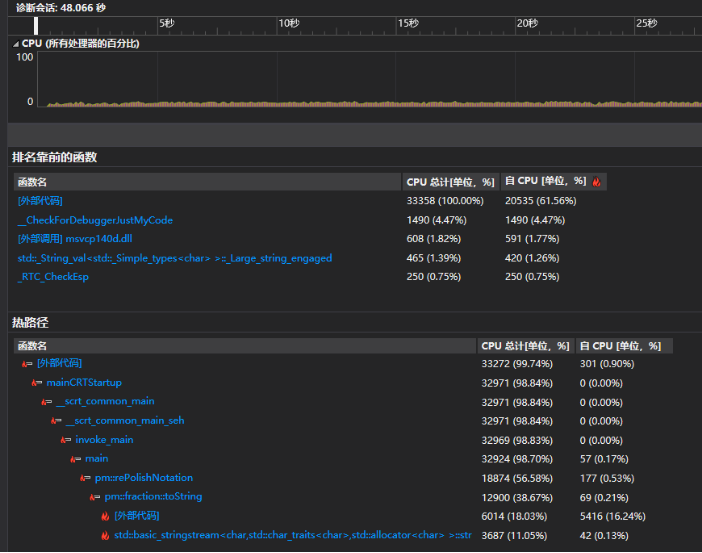
- 对生成题目做了生成10道题目的测式,可以发现波兰式计算结果的函数开销最大。
- 分数类的toString()方法因为多次调用也占用了许多CPU开销。
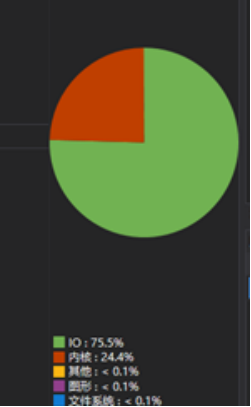
- IO操作为主要的操作
- 效能分析图：
  
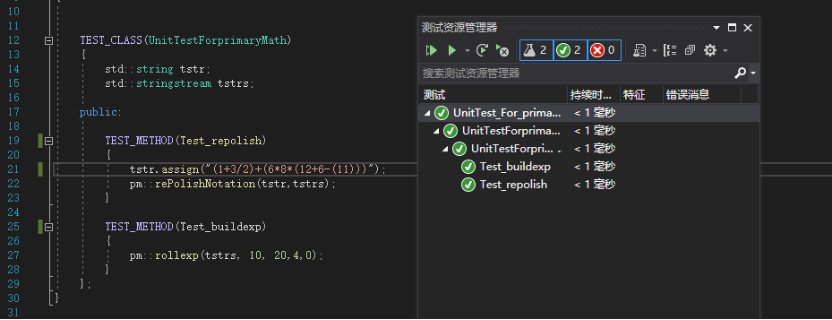
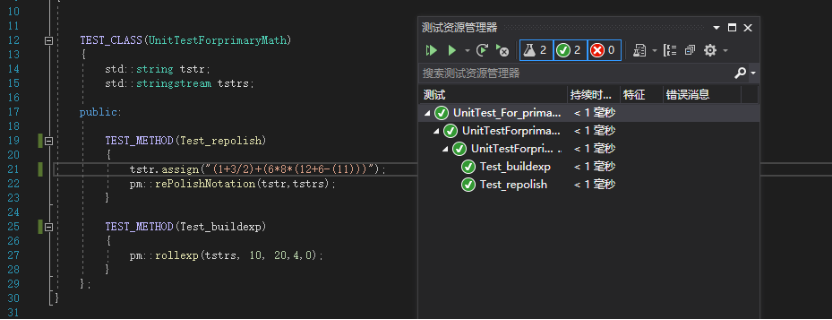
  *核心函数的单元测试：
测试用例
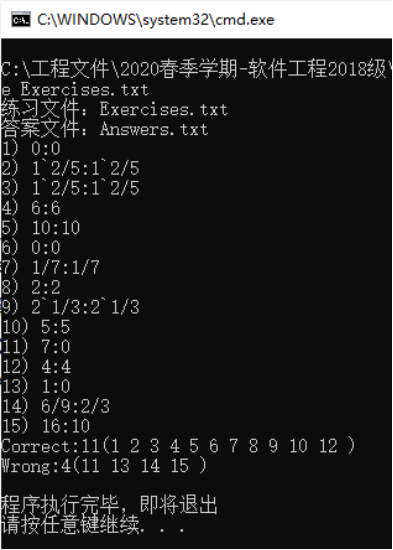
- 11，13，14，15题做错。

psp流程

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60	20
· Estimate	· 估计这个任务需要多少时间	60	20
Development	开发	2340	1570
· Analysis	· 需求分析 (包括学习新技术)	420	120
· Design Spec	· 生成设计文档	240	100
· Design Review	· 设计复审 (和同事审核设计文档)	180	120
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	180	30
· Design	· 具体设计	600	600
· Coding	· 具体编码	240	360
· Code Review	· 代码复审	240	120
· Test	· 测试（自我测试，修改代码，提交修改）	240	120
Reporting	报告	540	150
· Test Report	· 测试报告	360	30
· Size Measurement	· 计算工作量	120	30
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60	90
合计		2940	1740

总结
1. 对容器模板不够熟悉，导致部分代码采用数组形式组织，导致可能使用野指针
2. 结对编程与队友的交流不够，急于实现，编码之前的需求分析与设计准备不足，使得代码阶段非常艰难，常常由于粗心导致bug使得程序无法执行。

posted @ 2020-03-31 20:05 腊肠菌阅读(171) 评论(0) 收藏举报

刷新页面返回顶部

结对项目作业

公告