十大排序算法
十大排序
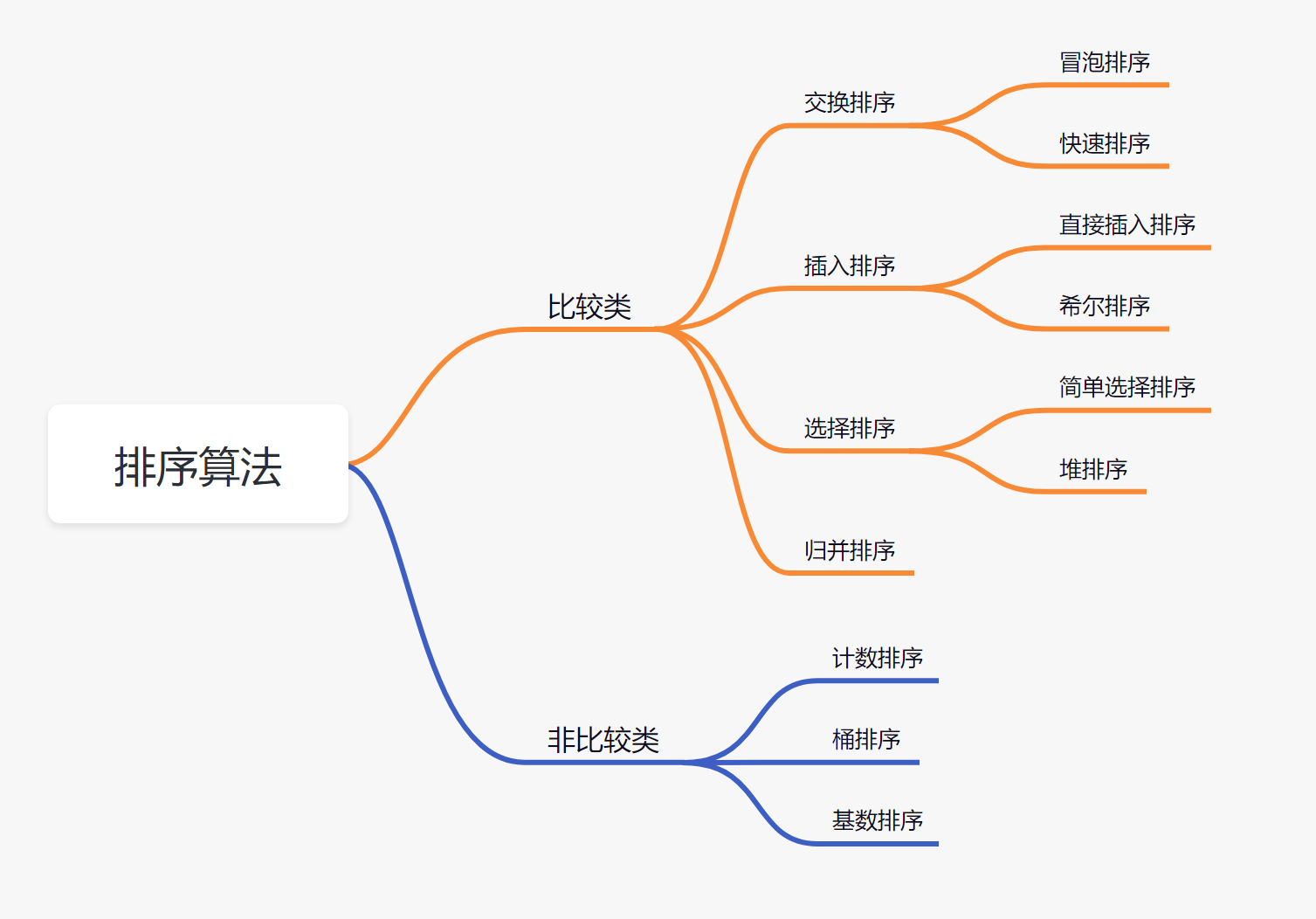
总结对比
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n) | O(n2) | O(1) | In-place | 稳定 |
| 选择排序 | O(n2) | O(n2) | O(n2) | O(1) | In-place | 不稳定 |
| 插入排序 | O(n2) | O(n) | O(n2) | O(1) | In-place | 稳定 |
| 希尔排序 | O(n log n) | O(n log2 n) | O(n log2 n) | O(1) | In-place | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | Out-place | 稳定 |
| 快速排序 | O(n log n) | O(n log n) | O(n2) | O(log n) | In-place | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | In-place | 不稳定 |
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(k) | Out-place | 稳定 |
| 桶排序 | O(n + k) | O(n + k) | O(n2) | O(n + k) | Out-place | 稳定 |
| 基数排序 | O(n x k) | O(n x k) | O(n x k) | O(n + k) | Out-place | 稳定 |
相关术语解释:
- 稳定:如果 a 原本在 b 前面,而 a=b,排序之后,a 仍然在 b 的前面
- 不稳定:不满足稳定定义
- 内排序(In-place):所有排序操作都在内存中完成
- 外排序(Out-place):由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行。
- 时间复杂度:一个算法执行所耗费的时间
- 空间复杂度:运行完一个程序所需内存的大小
- n:数据规模
- k:「桶」的个数
- In-place:不占用额外内存
- Out-place:占用额外内存
转载(里面也有对每个算法的总结、思路分析)
冒泡排序
每次循环都能找到数组中最大值冒泡至最后一位,以此达到排序的目的
优化:如果循环一遍没有发生值的交换,表明数组已经有序,便直接退出函数
#include<iostream>
using namespace std;
void swap(int &a, int &b) {
a ^= b;
b ^= a;
a ^= b;
}
//冒泡排序
void bubbleSort(int *arr, int length) {
//传入的数组长度小于2
if(length < 2) return;
for(int i = 0; i < length - 1; i++) {
//记录在一次内循环中是否发生了一次数的交换
bool flag = false;
//注意这里lenght-i,因为每一轮排序都会将最大值冒泡到最后的位置,它就不参与排序
for(int j = 1; j < length - i; j++) {
if(arr[j - 1] > arr[j]) {
swap(arr[j - 1], arr[j]);
flag = true; //表示发生了交换,说明数组还未排序完成
}
}
//在一次内循环中没有发生值的交换,说明以及排序完成,退出循环
if(flag == false) {
break;
}
}
}
int main() {
int arr[8] = {1, 56, 3, 2, 8, 3, 6, 7};
int length = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, length);
for(int i = 0; i < length; i++) {
cout<<arr[i]<<" ";
}
return 0;
}
选择排序
单元选择排序:每次循环都找到数组中的最小值(最大值),将其与首元素(尾元素)交换位置
双元选中排序:每次循环都找到数组中的最小值和最大值,将其与首元素和尾元素交换位置
//单元选择排序
void selectSort(int arr[], int length) {
if(length < 2) return;
for(int i = 0; i < length - 1; i++) {
//记录最小元素下标
int minIndex = i;
for(int j = i + 1; j < length; j++) {
//找到小的数,改变下标
if(arr[j] < arr[minIndex]) minIndex = j;
}
//如果存在最小值
if(minIndex != i) swap(arr[i], arr[minIndex]);
}
return ;
}
//双元选择排序
void selectSort(int arr[], int length) {
for(int i = 0; i < length; i++) {
int minIndex = i;
int maxIndex = length - i - 1;
//遍历整个数组
for(int j = i ; j < length - i ; j++) {
if(arr[j] > arr[maxIndex]) maxIndex = j;
if(arr[j] < arr[minIndex]) minIndex = j;
}
if(maxIndex == minIndex) break;
if(minIndex != i) swap(arr[minIndex], arr[i]);
//当最大值与最小值在两端时,上面已经交换过了,所以将maxIndex赋值,不在执行下面的交换两者的值
if(maxIndex == i) maxIndex = minIndex;
if(maxIndex != length - i - 1) swap(arr[maxIndex], arr[length - i - 1]);
}
return;
}
插入排序
从第二个数a[1]开始,每次循环指针依次向后移一位。如果a[i]前面存在比它大的数,那么从比它大的数的位置起依次向后移动一位,移动完毕再将a[i]插入它该插入的位置。
//简单插入排序
void insertSort(int arr[], int length) {
if(length < 2) return ;
for(int i = 1; i < length; i++) {
int temp = arr[i];
int j = i - 1;
//从后往前遍历 ,因为是从第二个数开始比较的,所以前面的都是有序的
for(; j >= 0; j--) {
//如果temp比前面的数小,那么temp前面的数向后移动
if(temp < arr[j]) arr[j + 1] = arr[j];
else break;
}
//发生了移动,将待填充的位置填入temp
if(j != i - 1) arr[j + 1] = temp;
}
return;
}
//折半插入排序
void insertSort(int arr[], int length) {
if(length < 2) return ;
for(int i = 1; i < length; i++) {
//如果顺序正确,直接跳过
if(arr[i - 1] < arr[i]) continue;
int temp = arr[i];
int left = 0, right = i - 1;
//二分查找 ,找到temp应该插入的位置
while(left <= right) {
int mid = (left + right) / 2;
if(temp >= arr[mid]) left = mid + 1;
else right = mid - 1;
}
for(int j = i; j > left; j--) {
arr[j] = arr[j - 1];
}
arr[left] = temp;
}
return ;
}
快速排序
标准快排
#include<iostream>
using namespace std;
void quickSort(int a[], int l, int r) {
int i, j, temp;
if(l < r) {
i = l, j = r;
temp = a[i]; //将第一个元素保存
while(i < j) {
while(i < j && a[j] >= temp) j--; //从右向左找到第一个小于temp的数
a[i] = a[j]; //移动到a[i],
while(i < j && a[i] <= temp) i++; //从左向右找到第一个大于temp的数
a[j] = a[i];
}
a[i] = temp;
quickSort(a, l, i - 1);
quickSort(a, i + 1, r);
}
}
int main() {
int a[] = {30,40,60,10,20,50};
int len = sizeof(a) / sizeof(a[0]);
quickSort(a, 0, len - 1);
for(int i = 0; i < len; i++) {
cout<<a[i]<<" ";
}
return 0;
}
取随机数为基准点的快排,比选第一个元素为基准点快,一般用这个,或者三路快排
include<stdlib.h>
要取得[a,b)的随机整数,使用(rand() % (b-a))+ a;
要取得[a,b]的随机整数,使用(rand() % (b-a+1))+ a;
要取得(a,b]的随机整数,使用(rand() % (b-a))+ a + 1;
#include<iostream>
#include<cstdlib>
using namespace std;
const int maxn = 1e5 + 10;
int a[maxn];
void quickSort(int a[], int l, int r) {
int i, j, temp;
if(l < r) {
i = l, j = r;
//快排优化:随机生成一个[l, r]区间的下标,将该下标的值与a[i]交换
int t = (rand() % (r - l + 1)) + l; //[r, l]的随机数
swap(a[i], a[t]);
temp = a[i]; //将第一个元素保存
while(i < j) {
while(i < j && a[j] >= temp) j--; //从右向左找到第一个小于temp的数
a[i] = a[j]; //移动到a[i]
while(i < j && a[i] <= temp) i++; //从左向右找到第一个大于temp的数
a[j] = a[i];
}
a[i] = temp;
quickSort(a, l, i - 1);
quickSort(a, i + 1, r);
}
}
int main() {
int n;
cin>>n;
for(int i = 0; i < n; i++) {
cin>>a[i];
}
int t = 0;
//特判是否已经排好序,不然会tle最后一个点
while(a[t] <= a[t + 1] && t < n - 1) t++;
if(t == n - 1);
else quickSort(a, 0, n - 1);
for(int i = 0; i < n; i++) {
cout<<a[i]<<" ";
}
return 0;
}
归并排序
#include<iostream>
using namespace std;
//合并
void Merge(int a[], int l, int mid, int r) {
int i = l, j = mid + 1, k = 0; //i表示第一个区间的第一个元素,j表示第二个区间第一个元素
int *temp = new int[r - l + 1]; //辅助数组
while(i <= mid && j <= r) {
//放入小一点的元素
if(a[i] <= a[j]) temp[k++] = a[i++];
else temp[k++] = a[j++];
}
//合并左右半区剩余元素
while(i <= mid) {
temp[k++] = a[i++];
}
while(j <= r) {
temp[k++] = a[j++];
}
//将辅助数组赋值到a[]
for(i = l, k = 0; i <= r;i++, k++) {
a[i] = temp[k];
}
delete []temp; //释放内存
}
//递归分块
void MergeSort(int a[], int l, int r) {
if(l == r) return; //当子序列长度为1时,结束
//有时候相加可能超过int范围可以使用mid = l + (r - l) / 2
int mid = (l + r) / 2;
MergeSort(a, l, mid);
MergeSort(a, mid + 1, r);
Merge(a, l, mid, r); //合并
}
int main() {
int a[8] = {3,1,2,4,5,8,7,6};
MergeSort(a, 0, 7);
for(int i = 0; i < 8; i++)
cout<<a[i]<<" ";
}
堆排序
先构建一个正经大根堆,再依次将堆顶最大元素和尾部元素交换,这样尾部元素就是最大值,同时将尾部剔除堆,再进行一次大根堆的构建...依次进行到最后,就变成升序了。
#include<iostream>
#include<algorithm>
using namespace std;
//构建大根堆
void max_heap(int a[], int start, int end) { //该大根堆从下标0开始算
int dad = start;
int son = dad * 2 + 1; //左子节点
while(son <= end) {
if(son + 1 <= end && a[son] < a[son + 1]) { //找到两个子节点中最大值
son++;
}
if(a[dad] > a[son]) return ;
else {
swap(a[dad], a[son]); //将大的值上浮
dad = son;
son = dad * 2 + 1;
}
}
}
//程序入口
void heap_sort(int a[], int len) {
for(int i = len / 2 - 1; i >= 0; i--) { //i从最后一个根节点开始
max_heap(a, i, len);
}
for(int i = len - 1; i >= 1; i--) {
swap(a[0], a[i]);
//每次循环都踢出去最后一个元素,因为它已经说最大的了
max_heap(a, 0, i - 1); //[0, i - 1]
}
}
int main() {
int a[5] = {2, 1, 5, 3, 4};
int len = sizeof(a) / sizeof(a[0]);
heap_sort(a, len);
for(int i = 0; i < len; i++) {
cout<<a[i]<<" ";
}
return 0;
}
希尔排序
希尔排序是在插入排序的基础上,进行了多次插入排序,每一次都会使数组更加有序。
思路:根据增量分组,每个相邻组的值一一对应,如果左边组对应的值大于右边,则进行一次swap
#include<iostream>
using namespace std;
void shell_sort(int a[], int len) {
for(int g = len / 2; g > 0; g /= 2) {
for(int i = g; i < len; i++) {
int j = i;
while(j - g >= 0 && a[j] < a[j - g]) {
swap(a[j], a[j - g]);
j -= g;
}
}
}
}
int main() {
int a[7] = {2, 9, 1, 3, 5, 3, 6};
shell_sort(a, sizeof(a) / sizeof(a[0]));
for(int i = 0; i < 7; i++) {
cout<<a[i]<<" ";
}
return 0;
}
计数排序
思想很简单,即用一个数组
c存储待排序数组a的每一个值并计数,用数组a的值作为数组c的下标并累加。例如:a[2, 1, 2, 2] --> c[1] = 1, c[2] = 3
#include<iostream>
#include<cstring>
using namespace std;
int Max = INT_MIN;
int Min = INT_MAX;
void maxn(int a[], int len) { //找最大值
for(int i = 0; i < len; i++) {
if(a[i] > Max) Max = a[i];
if(a[i] < Min) Min = a[i];
}
}
int main() {
int a[7] = {2, 9, 1, 3, 5, 3, 6};
int len = sizeof(a) / sizeof(a[0]);
maxn(a, len);
int c[Max - Min + 1]; //计数数组
memset(c, 0, sizeof(c));
//计数
for(int i = 0; i < len; i++) {
c[a[i] - Min]++; //[0, Max - Min]
}
//记录结果
int res[len];
int index = 0;
for(int i = 0; i < (Max - Min + 1); i++) {
while(c[i] > 0) {
res[index++] = i + Min;
c[i]--;
}
}
//输出
for(int i = 0; i < len; i++) {
cout<<res[i]<<" ";
}
return 0;
}
桶排序
按极值(最大值 - 最小值 + 1),决定桶的数量,
每个数为 / 10就是该数应放入的桶的编号
将不同数放入各自桶后再对各自桶内的数排序,这样将每个桶合并就是有序的了
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int mmax = INT_MIN;
int mmin = INT_MAX;
void Count(int a[], int len) {
for(int i = 0; i < len; i++) {
if(a[i] > mmax) mmax = a[i];
if(a[i] < mmin) mmin = a[i];
}
}
int main() {
int a[]= {1,8,7,44,42,46,38,34,33,17,15,16,27,28,24};
int len = sizeof(a) / sizeof(a[0]);
Count(a, len);
//极值分别为1和46,平均一个桶放10个,所以定义5个桶
int n = mmax / 10 - mmin / 10 + 1;
vector<vector<int>> t(n); //初始化为n行的二维数组
for(int i = 0; i < len; i++) { //遍历每个数,放入对应的桶内
int temp = a[i] / 10;
t[temp].push_back(a[i]);
}
for(int i = 0; i < n; i++) { //遍历每个桶
if(t[i].size() <= 1) continue;
sort(t[i].begin(), t[i].end()); //sort排序每个桶
}
int index = 0;
for(int i = 0; i < n; i++) { //将排序后的桶依次输出
for(int j = 0; j < t[i].size(); j++) {
if(t[i].size() == 0) continue;
a[index++] = t[i][j];
}
}
//输出结果
for(int i = 0; i < len; i++) {
cout<<a[i]<<" ";
}
return 0;
}
基数排序
思路
用10个桶,编号分别是0 ~ 9,每个桶大概放不确定个元素,数据多每个桶就开大一点
先获取数据中的最大值,最大值的位数
digits就是我们要循环的次数。每次循环都要对每个数 / n % 10取整,这样经过第一轮入桶,所有的个位数虽然在不同的桶内,但是从左到右每个桶来看就是有序的了。再进行一次循环对每个数 / n % 10取整,个位数都依次放入了0号桶且0号桶的个位数都是按顺序放入的,十位数的结果1 ~ 9也分别放入对应的编号桶中...这样直到循环到最后对最高位入桶,所有的数就都是有序的了
#include<iostream>
using namespace std;
int t[10][7]; //桶[0, 9]
int l[10]; //记录每个桶的长度
int m(int a[]) { //获取数组最大值
int mmax = INT_MIN;
for(int i = 0; i < 7; i++) {
if(a[i] > mmax) mmax = a[i];
}
return mmax;
}
int main() {
int a[7] = {2, 221, 21, 122, 12, 78, 1};
int mmax = m(a);
//最大值的位数就是要排序的轮数
int digits = 0;
while(mmax != 0) {
mmax /= 10;
digits++;
}
for(int j = 0, n = 1; j < digits; j++, n *= 10) {
for(int i = 0; i < 7; i++) {
//比如第一轮2放入2号桶,所以l[2]++;
int temp = a[i] / n % 10;
t[temp][l[temp]++] = a[i];
}
//因为每循环一次,桶里的数据会被覆盖,所以我们每循环一次都要将桶的数直接存起来
int index = 0;
for(int i = 0; i < 10; i++) { //遍历每个桶
if(l[i] == 0) continue; //桶没有元素
for(int k = 0; k < l[i]; k++) {
a[index++] = t[i][k];
}
l[i] = 0; //赋值结束初始化每个桶长度
}
}
for(int i = 0; i < 7; i++) {
cout<<a[i]<<" ";
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号