Algorithm 笔记

c/c++标准库

cstring

strlen(m) 字符串长度

strcmp(m, n) 字符串比较：相等返回0，m < n 返回负数，反之返回正数

strcpy(m, n) 字符串拷贝：将n复制给m

memset(arr, 0, sizeof(arr)) 暴力清空，每个元素都赋值为0。注意如果要对数组每个数赋相同的值，那个值不是0或-1，则最好选用fill函数

补充memset给每个值赋无穷大：memset(arr, 0x3f, sizeof(arr))

memcpy(m, n, strlen(n) + 1) 暴力拷贝，

strcat(m, n)字符串拼接，将n接在m后面

str.substr(m, n)，获得str中起点为m，长度为n的字符串

str.find(m, n)，从n位置开始在str中查找子串m，特别注意，没找到对应子串m应该用str.find(m, n) == string::npos判断

string str = "hello";

str.length();//O(n)
str.size();//O(n);

//在下标1位置插入字符串"aaa",O(n)
str.insert(1,"aaa");

//在迭代器处插入一个字符或字符串，O(n)
str.insert(str.begin(),'a');

//返回c语言字符串,即char数组，用于printf,O(n)
str.c_str();

//把str2拼接到str后面，O(n)
str.append(str2);

//strcmp(str2),
str.compare(str2);

str == str2;//strcmp(str,str2) == 0

str += str2;//str.append(str2)

str += 'a';//str.push_back('a');

cmath

三角函数，指数函数，浮点数取整函数

返回类型和调用类型都是double(round除外)

fabs(double x)

对x取整

floor(double x)、ceil(double x)

分别表示对x向下取整和向上取整，向下取整是不大于x，向上取整是不小于x

pow(double r,double p)

返回r的p次方，即r^p

sqrt(double x)

返回x的算术平方根

log(double x)

返回x以自然对数为底的对数

自然对数是以e为底的对数

sin(double x)、cos(double x)、tan(double x)

分别返回x的正弦值，余弦值，正切值

注意里面的x是弧度，需要用弧度转化公式。如弧度 = 角度 * Π / 180

asin(double x)、acos(double x)、atan(double x)、atan2()

注意这里x表示弧度是[-1，1]区间内的浮点数，1 rad = ${\frac {180^{\circ }}{\pi }}$

double acos(double x) 返回以弧度表示的 x 的反余弦

double asin(double x) 返回以弧度表示的 x 的反正弦

x∈ [-pi/2,+pi/2]

double atan(double x) 返回以弧度表示的 x 的反正切

y, x∈ [-pi,+pi]

double atan2(double y, double x) 返回以弧度表示的 y/x 的反正切

round(double x)

对x进行四舍五入操作，返回值是整数

取整

floor：向下取整

double floor(double x) 返回小于或等于 x 的最大的整数值

ceil：向上取整

double ceil(double x) 返回大于或等于 x 的最小的整数值

精度问题：因为浮点数存在精度的问题，不完全是一个整数，所以需要一个极小值控制取整的值

比如ceil向上取整，它的参数可能是3.00000070，如果这时向上取整就会取到4，所以需要减去一个极小值达到控制精度的目的

#define esp 1e-8;

double res = floor(res + esp);

double res = ceil(res - esp);

algorithm

max()、min()、abs()

max(x, y)返回两者最大值
min(x, y)返回两者最小值
abs(x) 返回x的绝对值，注意这里的x只能是整数，浮点数要使用math头文件下的fabs(x)函数
数组最大最小指针

min_element(arr.begin(),arr.end());

max_element(arr.begin(),arr.end());

swap()

复杂度O(1)
swap(x, y)用来交换x与y的值

reverse()

复杂度O(n)

reverse(it1, it2)可以将数组或者容器、字符串在指定范围[it1, it2)内进行反转

#include<iostream>
#include<algorithm>
using namespace std;

int main(){
	int arr[10] = {1, 3, 2 ,4 ,7 ,3};
	reverse(arr, arr + 5);
	for(int i = 0; i < 6; i++) {
		cout<<arr[i]<<" ";
	}
 	return 0;
}
//输出：
7 4 2 3 1 3

next_permutation()

next_permutation(arr, arr + 3)根据字典序对序列进行全排列

#include<iostream>
#include<algorithm>
using namespace std;

int main(){
	int arr[10] = {1, 2, 3};
	//注意这里要使用do~while，因
	do {
		cout<<arr[0]<<" "<<arr[1]<<" "<<arr[2]<<endl;
	}while(next_permutation(arr, arr + 3));
 	return 0;
}
//输出：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

fill()

将数组或容器中的某一段区间赋为某个相同的值，与memset不同的是，fill的赋值是可以选择范围的，而memset的赋值是整个数组

#include<iostream>
#include<algorithm>
using namespace std;

int main(){
	int a[10] = {1, 3 ,4 ,5, 6};
	fill(a, a + 3, 200);
    // 更新二维数组
    int b[10][20];
    fill(b[0], b[0] + 10 * 20, 200);
	for(int i = 0 ; i < 5; i++){
		//TODO
		cout<<a[i]<<" ";
	}
}
//输出：
200 200 200 5 6

sort()

复杂度O(nlog_n)

排序函数，可以对数组、容器、结构体进行排序

//默认升序排列
//数组
int arr[] = {1,3,2,4,1};
sort(arr,arr+5);
sort(arr, arr + 3,cmp)	//对[0, 2]进行排序

//容器
vector<int> arr {1,3,2,4,1};
sort(arr.begin(),arr.end());
sort(arr.begin(), arr.end(), [](int a, int b) {
    return a < b;
});	// lambda表达式

// 二维vector排序，根据第一个元素升序，第二个元素降序排序
sort(arr.begin(), arr.end(), [](const auto &e1, const auto &e2) {
            return e1[0] < e2[0] || (e1[0] == e2[0] && e1[1] > e2[1]);
        })
    
//结构体

//升序
    sort(arr, arr + 3, greater<int>)
//降序
    sort(arr, arr + 3, less<int>)

可以通过实现cmp()，进而实现自定义排序方式，如降序、升序、字典序等等

//自定义排序
int cmp(int a,int b){
    return a > b;	//降序排列
}
int main(){
    int arr[] = {1,3,2,4,1};
	sort(arr,arr+5,cmp);
    for(int i = 0;i < arr.length();i++){
        cout<<arr[i]<<endl;
    }
    return 0;
}

lower_bound()和upper_bound()

lower_bound(first, last, val)用来寻找在数组或容器的[first, last)范围内的第一个大于等于val的元素的位置的指针
upper_bound(first, last, val)用来寻找在数组或容器的[first, last)范围内的第一个大于val的元素的位置的指针

int main(){
	int a[10] = {1, 2, 2, 3, 3, 3, 5, 5 , 5, 5};
	//分别是大于等于和大于，由于返回值是一个指针，所以减去首地址就是返回那个元素的下标
	cout<<lower_bound(a, a + 10, 3) - a<<" "<<upper_bound(a, a + 10, 3) - a<<endl;
	return 0;
}
//输出:
3  6

nth_element

把数组中第n小（从0开始算）的数放到第n个位置 O(n)

用于查找某个排好序后的元素应该放在的位置，并保证它左边的数比它小，右边的数比它大，但是未进行排序

nth_element(arr.begin(),arr.begin() + n,arr.end());

查找最大的元素：int res = *max_element(arr.begin(), arr.end());

查找最小的元素：int res = *min_element(arr.begin(), arr.end());

vector<int> arr {3,4,1,2,5};

int main(){
	nth_element(arr.begin(),arr.begin()+3,arr.end());
	vector<int>::iterator p;
    for(p = arr.begin();p != arr.end();p++){
        cout<<*p;
    }
    return 0;
}
//输出；21345

unique

对已经排好序的数组进行去重 O(n)

unique的本质是将重复的元素移到数组末尾，需要在sort之后使用，大多数情况用于离散化

int newLength = unique(arr.begin(),arr.end()) - arr.begin();

#include<bits/stdc++.h>
using namespace std;

int main() {
	int a[10] = {-1, 1, 3, 3, 2, 5, 2, 8, 5};
	sort(a + 1, a + 8);
	for (int i = 0; i <= 8; i++) {
		cout << a[i] << ' ';
	}
	cout << "\n";
    //返回新的去重后的长度
	int len = unique(a + 1, a + 8) - (a + 1);
	for (int i = 0; i <= len; i++) {
		cout << a[i] << ' ';
	}
	return 0;
}
//输出
-1 1 2 2 3 3 5 8 5
-1 1 2 3 5 8

binary_search

查找对应元素是否存在 O(logn)

bool isExist = binary_search(arr.begin(),arr.end(),1);

cstdlib

qsort() 快排

rand() 随机数

malloc() free() c语言动态分配内存

atoi

将char数字字符串'12313'转化为int型的12313

//char-->int
char str[20];
cin>>str;
int i = atoi(str);
cout<<i;

//string-->int
string s;
int t = atoi(s.c_str());

itoa

(int value, char *string, int radix)：将十进制转化为任意进制

value是传入的十进制数

string是结果字符数组

radix是目标进制

int n = 10;
char a[20];
itoa(n, a, 2);
cout<<a;
//输出：1010

ctime

time(0) 从1970年到现在的秒数（配合随机数使用 srand(time(0))）

clock() 程序启动到目前位置的毫秒数

cctype

isdigit()，isalpha()，判断字符是否为数字、大小写字母

isspace() 检查所传的字符是否是空白字符

空白字符包括：

' '     (0x20)    space (SPC) 空格符
'\t'    (0x09)    horizontal tab (TAB) 水平制表符    
'\n'    (0x0a)    newline (LF) 换行符
'\v'    (0x0b)    vertical tab (VT) 垂直制表符
'\f'    (0x0c)    feed (FF) 换页符
'\r'    (0x0d)    carriage return (CR) 回车符

处理单个字母

islower() : 判断字母是否是小写，小写字符则返回2，反之返回0

isupper() : 判断字母是否是大写，大写字符则返回1，反之返回0

toupper() : 将小写字母转化为大写字母，返回值是对应的ascll码

tolower() : 将大写字母转化为小写字母，返回值是对应的ascll码

处理字符串

strupr() : 将字符串全部转化为大写

strlwr() : 将字符串全部转化为小写

char a;
cin>>a;
char s[10] = "daDA";
cout<<"小写："<<islower(a)<<endl;
cout<<"toupper："<<char(toupper(a))<<endl;
cout<<"strupr："<<strupr(s)<<endl;
cout<<"大写："<<isupper(a)<<endl;
cout<<"tolower："<<char(tolower(a))<<endl;
cout<<"strlwr："<<strlwr(s);

//输入
a
//输出
小写：2
toupper：A
strupr：DADA
大写：0
tolower：a
strlwr：dada

其他

__builtin_popcount()

返回数的二进制中1的个数

c++STL

vector 数组

vector<int> arr(100); //数组

vector<int> list; //链表

list.push_back(1);

#include<vector>
#include<iostream>
using namespace std;

vector<int> arr1(100);
vector<int> list;
int arr2[100];
char str[100];

int main(){
	//迭代器 
	vector<int>::iterator p1;
    //arr1.end()不是指向最后一个元素，是指向最后一个元素的下一个地址，是空的
	for(p1 = arr1.begin();p1 != arr1.end();p1++){
		cout<<*p1<<endl;
	}
	//普通指针
	int i;
	int *p2;
	for(p2 = arr2,i = 0;i < 100;i++,p2++){
		cout<<*p2<<endl;;
	}
	char *p;
	for(p = str;*p;p++){
		cout<<*p<<endl;
	}
	return 0;
}

vector初始化

vector<int> name(10, 1);	//定义一个初始大小为10，且每一位值都是1的向量

//这样定义就相当于定义了一个每一维都是长度可变的二维数组
vector<vector<int> > name;	//注意这里的> >之间是要加上空格的
//定义一个初始大小为10行5列的二维数组
vector<vector<int> > name(10, vector<int>(5));

vector<int> vi[100];	//这样vi[0]~vi[99]中每一个都是一个长度可变的vector容器

vector常见操作

list.resize(5);// 设置容器大小为5，并删除后面多余的元素

list.size();//数组元素个数，O(1)复杂度

list.clear();//一键清空数组，O(n)

list.empty();//判断数组是否为空，O(1)

list.begin();//数组的首元素迭代器,O(1)

list.end();//数组的最后一个元素的下一个元素的迭代器，该元素在数组中实际并不存在,O(1)

list.push_back(1);//往数组后面添加元素，O(1)

list.pop_back();//删除数组最后一个元素，O(1)

insert():
对于向指定位置插入元素，有两种方法
    1. vi.insert(it, i)，一次能够插入多个元素
    	vi.insert(vi.begin() + 2, 1); //向vi[2]位置插入一个元素1，后面的元素依次向后移位
		vi.insert(vi.begin(), 3, 1);向vi[0]前面插入3个1

	2. vi.emplace(it, i),与insert功能相同，但是一次只能插入一个元素
        vi.emplace(vi.begin(), 1);	//向最前面插入一个1

erase(): 
	1. 删除一个指定位置元素
        erase(it);
		erase(vi.begin() + 2);	//删除vi[2]位置的元素，其后面的元素依次进位
	2. 删除指定区间的元素
        erase(first, last)	//删除[first, last)的元素
        erase(vi.begin() + 1, vi.begin() + 5);	//删除vi[1]/vi[2]/vi[3]/vi[4]

stack 栈：后进先出

stack<int> sta;

sta.push(1);	//入

int topElement = sta.top();	//栈顶元素

sta.pop();	//出

sta.empty();	//判断是否为空

sta.size();

queue 队列

//队列，先进先出
queue<int> que;
que.push(1);
int frontElement = que.front();	//返回栈顶元素
que.pop();
que.empty();
que.size();
//优先队列
priority_queue<int> que2;
que2.push(1);
int minElement = que2.top();
que2.pop();
que2.empty();
que2.size();

priority_queue优先队列

priority_queue(int, vector<int>, greater<int>)	小根堆

priority_queue(int, vector<int>, less<int>)	大根堆
    
make_heap()将容器变为堆，默认是大根堆
vector<int> a(50);
make_heap(a.begin(), b.end());
make_heap(a.begin(), b.end(), greater<int>());
make_heap(a.begin(), b.end(), less<>());	// 小根堆
pop_heap(a.begin(), b.end())	// 将第一个与最后一个元素交换位置，再对前1~n - 1个元素进行make_heap
push_heap(a.begin(), b.end())	// 将最后一个元素放到堆的正确位置，需要先push_back(x)
pop_back(x)	// 移除容器最后一个元素x
push_back(x)	// 向容器末尾添加一个元素x

常用操作

push(const T& obj)：将obj的副本放到容器的适当位置，这通常会包含一个排序操作。
push(T&& obj)：将obj放到容器的适当位置，这通常会包含一个排序操作。
emplace(T constructor a rgs...)：通过调用传入参数的构造函数，在序列的适当位置构造一个T对象。为了维持优先顺序，通常需要一个排序操作。
top()：返回优先级队列中第一个元素的引用。
pop()：移除第一个元素。
size()：返回队列中元素的个数。
empty()：如果队列为空的话，返回true。
swap(priority_queue<T>& other)：和参数的元素进行交换，所包含对象的类型必须相同。

每次队首的元素都是优先级最大的元素

优先队列实现哈夫曼树

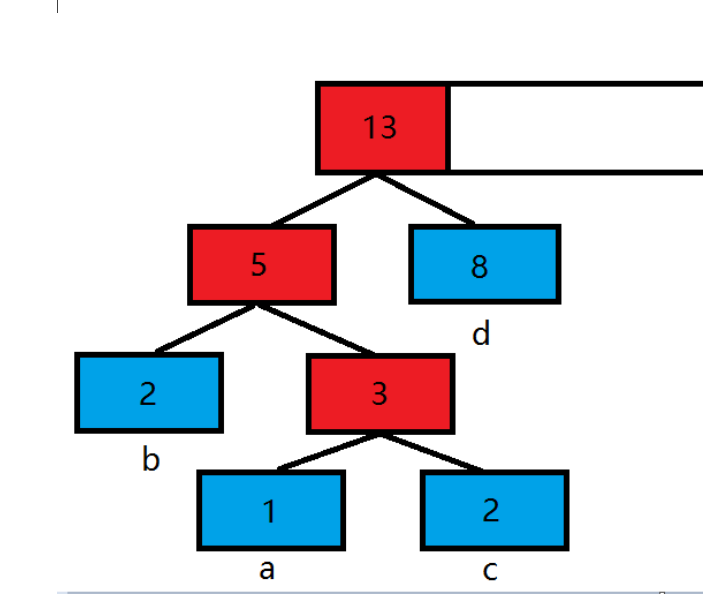
#include <queue>
#include <iostream>
using namespace std;
int main()
{
    int n,a,b,c;
    priority_queue<int,vector<int>,greater<int> >q;	//升序
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>c;
        q.push(c);
    }
    int ans=0;
    while(q.size()>1){
        a=q.top();q.pop();//取出最小的两个元素
        b=q.top();q.pop();
        cout<<a<<" "<<b<<endl;
        ans=a+b;//合并
        //哈曼夫树求解最小路径长度，ans += a + b; q.push(a + b);，最后的ans就是最小路径长度
        q.push(ans);//将合并后的数加入到队列中
    }
    cout<<ans<<endl;//最后编码总长度
    return 0;
}
//输入：
4
1 2 2 8
//输出：
1 2
2 3
5 8
13

deque双端队列

主要用于频繁对队列两端做增删的情况，

set集合

O(logn)

set是一个内部有序且不含重复元素的容器，有自动排序和去重复元素的作用，底层是平衡树

//集合，自带去重
#include<set>	//头文件

//定义一个set
set<typename> name;
set<int> name;

//定义一个set数组
set<typename> arr[size];
set<int> arr[100];

//注意set只能通过迭代器访问
set<int>::iterator it;
for(it = name.begin(); it != name.end(); it++) {
	cout<< *it<<endl;
}

//常用方法
insert(x)
    插入x元素，并自动进行排序和去重，时间复杂度是O(logn)
find(value)
    返回set中值为value的迭代器
    1. 
        set<int>::iterator it = name.find(2);
        cout<<*it<<endl;
	2. 
        cout<<*(name.find(2))<<endl;
erase()
    1. erase(it)，删除单个元素，其中it是迭代器，时间复杂度是O(1)
    	erase(name.find(2));
	2. erase(value)，删除单个元素，其中value是一个值，时间复杂度是O(logN)
        erase(2);
	3.erase(first, last)，区间[first, last)，时间复杂度是O(last - first)
        erase(name.find(2), name.find(5));	//删除[2,5)的元素
clear()
size()

multiset ：不去重

//多重集合，允许元素重复
multiset<int> mst;
mst.insert(1);
mst.insert(1);
mst.count(1);	//获取元素数量

unordered_set：不排序，去重

map 映射

map有两种数据结构，时间复杂度都是O(logn)

第一种是pair：可以由两种任意数据类型构成

第二种是map：是一个超级数组，会对数组内容自动按照key升序进行排序

//pair
pair<int,int> origin;
origin = make_pair(0,0);
origin.first == origin.second;


pair<string,int> id;
id = make_pair("小明",180);

//map
map<string,int> studentHeight = 
{
    {"小明",180},
    {"小红",160}
}
//studentHeight["小明"] = 180;
//studentHeight["小红"] = 160;
studentHeight.insert(id);
StudentHeight.erase("小明");

补充：#include<unordered_map>和#include<unordered_set>分别是基于哈希的set和map的另一种实现版本，对每种元素都提供了计算哈希的函数。这两种数据结构不允许按大小顺序遍历元素，但是能够O(1)地访问和添加一个元素

bitsit 位集合

是一个只由0和1构成的数组，占用空间较小

用于状态压缩动态规划

bitsit<1000> bst;
bst[0] = 1;
bst.set(0);
bst[0] = 0;
bst.reset(0);
bst << 1;
bst >> 1;
bst ^= 1;
bst &= 1;
bst.count();
bst.to_string();
bst.to_ullong();

知识点补充

万能头文件

#include<bits/stdc++.h>

数组最大范围

int型一维数组：小于4e8，即4亿

int型二维数组：小于2e4，即2万

数据类型范围

int和long都是用32位来存储最大值和最小值分别为2147483647（2³¹-1 ~ 10⁹）， -2147483648(-2³¹)；

long long 是用64位来存储最大值和最小值分别为9223372036854775807（10¹⁸），-9223372036854775808；

float的最大值和最小值分别为3.40282e+038（10³⁸），1.17549e-038（10^-38）；

double的最大值和最小值分别为1.79769e+308（10³⁰⁸），2.22507e-308（10^-308）

INT_MIN：最小值

INT_MAX：最大值

数据量与复杂度

数据量	复杂度
10	O(n!)
20	O(2ⁿ)
500	O(n³)
2500	O(n²)
10⁶	O(nlog_n)
10⁷	O(n)
10¹⁴	O(n^1/2)
10²⁰	O(log_n)

读入字符串

char ch[20];
cin>>ch;	//只能读入一行不带空格、tab、换行的字符串

cin.getline(ch, 20);	//最长可以读入19个字符串，最后一个是'\0'，允许带空格

string str;
getline(cin, str);	//随便读入

//getchar与putchar
getchar用于读入单个字符，putchar用于输出单个字符

//gets与puts
gets(char *str)与puts(char *str)，分别表示读入和输出一行字符串

注意在使用c++的输入cin与getline时，如果是先使用cin再使用getline，中间需要用一个cin.ignore()读走cin的回车，否则会直接跳过本次getline的读入

获取随机数

#include<stdlib.h>

要取得[a,b)的随机整数，使用(rand() % (b-a))+ a;
要取得[a,b]的随机整数，使用(rand() % (b-a+1))+ a;
要取得(a,b]的随机整数，使用(rand() % (b-a))+ a + 1;

位运算

7个位运算（&，|，^，~，>>，<<，>>>）

按位与&：两个全为1，结果为1，否则为0
a, b两个数按位与的话，结果一定小于等于a和b

num &= num - 1; // 最低的 1 变成 0
6    & 5    => 4
0110 & 0101 => 0100


// 还可以通过(n & 1)判断n的奇偶性，因为二进制一个偶数的最后一位一定是0，奇数一定是1（二进制除了尾数其他都是2
的阶乘，他们的和一定是偶数，所以只用判断末尾就能判断奇偶）
按位或|：两位有一个为1，结果为1，否则为0
num |= num + 1; // 最低的 0 变成 1
6    | 7    => 7
0110 | 0111 => 0111
按位异或^：相同为0，不同为1

按位取反~：0->1,1->0

算术右移>>：低位溢出，符号位不变，并用符号位补溢出的高位

算术左移<<：符号位不变，低位补0

“>>>”：逻辑右移也叫无符号右移，运算规则是：低位溢出，高位补0

函数传参数组长度问题

函数传递一个数组时传入的是指针，在函数内不能得到数组的长度，需要手动传递长度

typedef

用于给数据类型取别名

#include <stdio.h>
typedef long long LL;	//给long long 取别名为LL，这样使用此数据类型时就可直接使用别名

int main() {
    LL a = 123456789;
    printf("%lld", a);
	return 0;
}

符号常量与const常量

符号常量又称宏定义，是替换的意思，就是将用到标识符的对应位置替换成常量3.14，

const是赋值，将值赋给常量

//符号常量
#define 标识符 常量值
#define PI 3.14

//const常量
const 数据类型 常量名 = 常量值
const double PI = 3.14;

注意define后面没有分号;，const后面有分号

推荐使用const，因为宏定义还能够表示一个片段，有时会出现错误

#include<stdio.h>
#define cal(x) (x * 2 + 1)

int main() {
	printf("%d\n", cal(1 + 2));
	return 0;
}
//输出：6

或许会认为输出的会是7，但是要知道宏定义表示的是替换的意思，直接将1+2代入到了表达式中，为1+2*2+1，所以结果为6

浮点数的比较

如果要判断两个浮点数相等，需要用到eps = 1e-8，进行如下操作

const double eps = 1e-8;

fabs((a) - (b)) < eps	//这样才能判断两浮点数相等，否则可能出错

同理我们可以通过eps这个极小的数来判断两个数的大小关系

Π

#include<stdio.h>
#include<math.h>

int main() {
	double PI = acos(-1.0);
	printf("%f\n", PI);
}
//输出：3.141593

进制转换

进制符号前缀表示

二进制：0b或0B（是数字0，不是字母O）

八进制：0

十六进制：0x

整数：

十进制转k进制：除k取余法，将结果取倒数

k进制转十进制：从最右边开始，每位数乘以k的位数-1次方，最后将每一个结果相加

二进制转八进制：从低位开始，每3个二进制一组的结果拼接，不足3位往高位补0

二进制转十六进制：从低位开始，每4个二进制一组的结果拼接，不足4位往高位补0

八进制转二进制：从低位开始，将每个数转为3位的二进制

十六进制转二进制：从低位开始，将每个数转为4位的二进制

小数：

十进制小数转k进制：将小数乘k，将结果的整数保存起来。重复上述操作，直到小数部分为0。将整数部分按顺序组合就是小数的二进制表示。简称：乘k取整，顺序排列

注意：小数的进制转换可能会出现无限循环的情况

二进制转十进制：将小数每个数乘以2^—位数，

二进制转八进制：将小数部分每3位一组做二进制表示，不足3位往低位补0，将结果拼接

二进制转十六进制：将小数部分每4位一组做二进制表示，不足4位往低位补0，将结果拼接

注意：

8进制（%o）与10进制（%d）与16进制（%x）的直接相互转换，可以直接通过c语言自带的sacnf与printf的格式限定符完成

二进制减法

当遇到0 - 1的情况时，需要从前借一位，如10 - 01 = 0(10) - 01 = 1，这里的0(10)中的10其实就是十进制的2

参考链接

原码、反码、补码

1、二进制的最高位是符号位：0表示正数，1表示负数（0->0，1->-）

2、正数的原码，反码，补码都一样

3、负数的反码 = 它的原码符号位不变，其他位取反（0->1，1->0）

4、负数的补码 = 它的反码+1；负数的反码 = 负数的补码-1

5、0的反码、补码都是0

6、在计算机运算时，都是以补码的方式来运算的

7、当我们在看运算结果时，要看它的原码

8、一个负数的二进制用其正数的补码表示

输入输出

基本格式

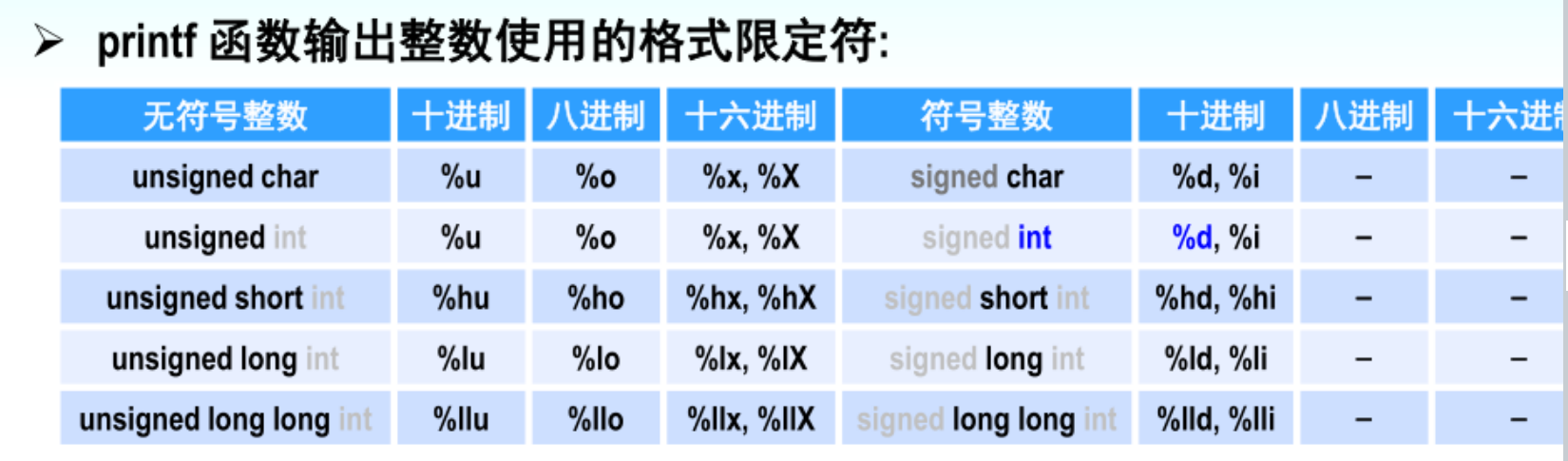
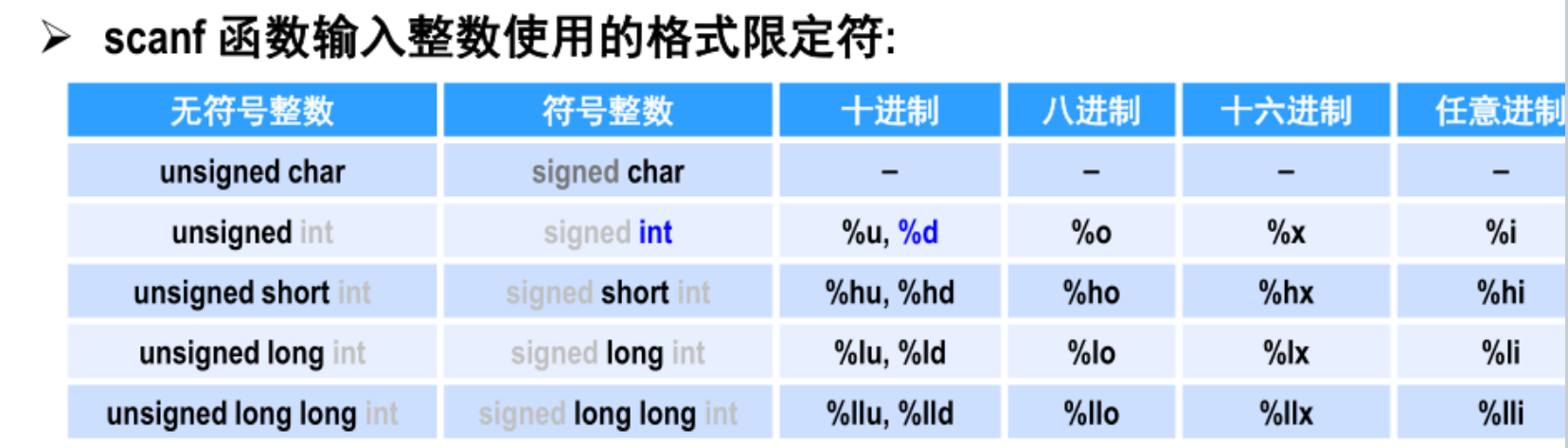
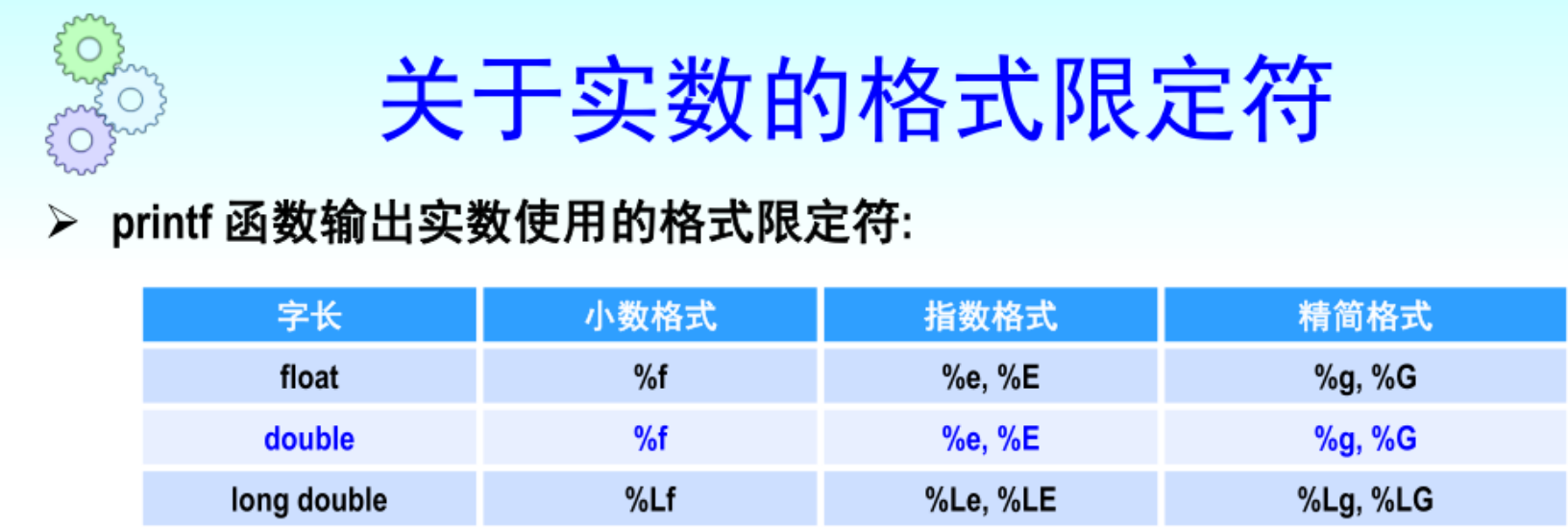
%g能够精简格式，并去掉末尾多余的0

sscanf和sprintf

sscanf（从左至右）

#include<stdio.h>

int main() {
	int n;
	char str[10] = "123";
	sscanf(str, "%d", &n);
	printf("%d\n", n);
	return 0;
}
//输出：123

sscanf(str, "%d", &n)就是将数组str中的内容以%d的形式写入n中

sprintf（从右至左）

#include<stdio.h>

int main() {
	int n = 223;
	char str[10];
	sprintf(str, "%d", n);
	printf("%s\n", str);
	return 0;
}
//输出：223

#include<stdio.h>

int main() {
	int n = 223;
	char str[10];
	sprintf(str, "%d", n);
	for(int i = 0; i < 10; i++) {
		printf("%d ", str[i] - '0');
	}
	return 0;
}
//输出：2 2 3 -48 -48 -48 -48 -48 -47 -48
//可知sprintf是一位一位存进字符数组的，并且在数组中是字符形式

sprintf(str, "%d", n)就是将n的值以%d的形式传给数组str

lambda表达式

格式：

[外部变量访问方式说明符] (参数) mutable noexcept/throw() -> 返回值类型
{
   函数体;
};
// （mutable noexcept/throw() -> 返回值类型）都可省略
auto display = [](int a,int b) -> void{cout << a << " " << b;}
auto display = [](int a,int b) {cout << a << " " << b;}

function<int(int a, int b)> cmp = [&](int a, int b) {
	return a > b;
}

外部变量格式	功能
[]	空方括号表示当前 lambda 匿名函数中不导入任何外部变量。
[=]	只有一个 = 等号，表示以值传递的方式导入所有外部变量；
[&]	只有一个 & 符号，表示以引用传递的方式导入所有外部变量；

.与->的区别

.主要用于类对象，->用与指针引用其成员

class A {
    int a;
}
A p;
A *q;
p.a;	// 对象
q->a;	// 指针

for(auto &i:s)和for(auto i:s)的区别

前者是引用类型，可以对s进行修改，后者不能修改s，形如void swap(int a, int b) 与 void swap(int &a, int &b)

数学问题

最大公约数

辗转相除法

int gcd(int a, int b) {
	if(b == 0) return a;
	return gcd(b, a % b);
}

最小公倍数

根据最大公约数得出最小公倍数

步骤：

先求得a与b的最大公约数d
用a * b / d结果就是要求得的最小公倍数，为了防止数据溢出，也可以写为a / d * b

对分数的处理

#include<bits/stdc++.h>
using namespace std;

int gcd(int a, int b) {
	if(b == 0) return a;
	else gcd(b, a % b);
}

struct Fraction {
	int up, down;	//分子、分母
}p[3];

//对分数进行处理
Fraction reduction(Fraction result) {
	if(result.down == 0) {	//分子为0 
		result.down = 1;
	}
	if(result.down < 0) {
		result.down = -result.down;
		result.up = -result.up;
	}
	else {
		//约分化简 
		int d = gcd(result.up, result.down);	//最大公约数 
		result.up = result.up / d;
		result.down = result.down / d;
	}
	return result;
}

//分数加法 
Fraction add(Fraction f1, Fraction f2, Fraction result) {
	result.up = f1.up * f2.down + f2.up * f1.down;
	result.down = f1.down * f2.down;
	return reduction(result);
}

//分数乘法
Fraction mult(Fraction f1, Fraction f2,Fraction result) {
	
	result.up = f1.up * f2.up;
	result.down = f1.down * f2.down;
	return reduction(result);
}

//输出
void showResult(Fraction res) {
	res = reduction(res);	//化简
	if(res.down == 1) cout<<res.up<<endl;	//分母为1，输出整数
	else cout<<res.up<<"/"<<res.down<<endl;
} 

int main() {
	p[0].up = 10; 
	p[0].down = 4;
	p[1].up = 7;
	p[1].down = 3;
	showResult(p[0]);
	showResult(p[1]);
	showResult(add(p[0], p[1], p[2]));
	showResult(mult(p[0], p[1], p[2]));
	return 0;
}
//输出
5/2
7/3
29/6
35/6

素数

素数即在2~n-1范围内大于1并且只有1和自身两个约数的数，我们可以缩小范围至2~sqrt(n)

普通方法求素数，时间复杂度是O(n * sqrt(n))，如果数据量超过了10⁵则不行了

#include<bits/stdc++.h>
using namespace std;
//求解100以内的素数 v

int maxn = 101;
int num = 0;
int res[101];
bool p[101];
 
bool isPrime(int n) {
	for(int i = 2; i <= sqrt(n); i++) {
		if(n % i == 0) return false;
	}
	return true;
}

void Build_Prime() {
	
	for(int i = 2; i < maxn; i++) {
		if(isPrime(i)) {
			res[num++] = i;
//			p[i] = true;
		}
	}	
}

int main() {
	Build_Prime();	//建表
	for(int i = 0; i < num; i++) {
		cout<<res[i]<<" ";
	} 
	return 0;
}
//输出
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

埃氏筛法

#include<bits/stdc++.h>
using namespace std;
//求解100以内的素数

const int maxn = 101;
int num = 0;
int res[maxn] = {0};
bool p[101];	//初始化都是0，即false

void Build_Prime() {
	for(int i = 2; i <= maxn; i++) {
		if(p[i] == 0) {
			res[num++] = i;	//存素数 
//			p[i] = true;
//			4 6 8 10...
//			6 9 12 15...
//			8 12 16...
			for(int j = i * i; j <= maxn; j += i) {
				p[j] = 1;	//存判断条件 
			}
		}
	}
}

int main() {
	Build_Prime();	//建表
	for(int i = 0; i < num; i++) {
		cout<<res[i]<<" ";
	}
	return 0;
}

质因子分解

先获取n以内的素数表，再定义一个结构体

struct factor {
    int x;	//因子
    int cnt;	//该因子个数
};

对sqrt(n)以内的数进行判断能否对n取余，如果能就代表是n的因子，
不断对这个数取余并操作，得到这个因子的个数，
操作到最后得到的n如果是1，则取余完成，如果不是1，则n是一个素数，只有两个因子，一个是1，另一个是它本身

大整数四则运算

对于一个大整数，应该将其存入数组中，再进行操作

#include<bits/stdc++.h>
using namespace std;

struct bign {
	int d[1000];
	int len;
	bign() {
		memset(d, 0, sizeof(d));
		len = 0;
	}
};

//将整数转化为数组 
bign change(char ch[] ) {
	bign a;
	a.len = strlen(ch);
	for(int i = 0; i < a.len; i++) {
		a.d[i] = ch[a.len - i - 1] - '0';
	}
	return a;
}
//加法 
bign add(bign a, bign b) {
	bign c;
	int carry = 0;	//进位 
	for(int i = 0; i < a.len || i < b.len; i++) {
		int temp = a.d[i] + b.d[i] + carry;
		c.d[c.len++] = temp % 10;
		carry = temp / 10;
	}
	if(carry != 0) {	//当两个数相加到最高位时，可能会进一位 
		c.d[c.len++] = carry;
	}
	return c; 
}

//减法
bign sub(bign a, bign b) {
	bign c;
	for(int i = 0; i < a.len || i < b.len; i++) {
		if(a.d[i] < b.d[i]) {
			a.d[i + 1]--;	//高位借1 
			a.d[i] += 10;
		}
		c.d[c.len++] = a.d[i] - b.d[i];
	}
	while(c.len - 1 >= 1 && c.d[c.len - 1] == 0) {	//当最高位是0时去掉 
		c.len--;
	} 
	return c;
} 

//乘法,与学过的乘法不同 
bign mult(bign a, int b) {
	bign c;
	int carry = 0;
	for(int i = 0; i < a.len; i++) {
		int temp = a.d[i] * b + carry;
		c.d[c.len++] = temp % 10;
		carry = temp / 10;
	}
	while(carry != 0) {	//乘法进位可能不止一位 
		c.d[c.len++] = carry % 10;
		carry /= 10; #
	}
	return c;
}

//除法
int r = 0;
bign divide(bign a, int b) {	//r为余，初始应为0 
	bign c;
	
	c.len = a.len;	//被除数和商长度一一对应，相等 
	for(int i = a.len - 1; i >= 0; i--) {	//从高位开始 
		r = r * 10 + a.d[i];
		if(r < b) c.d[i] = 0;
		else {
			c.d[i] = r / b;
			r = r % b;
		}
	}
	//去掉高位的0 
	while(c.len - 1 >= 1 && c.d[c.len - 1] == 0) {
		c.len--;
	}
	return c;
}
 
void print(bign a) {
	for(int i = a.len - 1; i >= 0; i--) {
		printf("%d", a.d[i]);
	} 
}

int main() {
	char str1[1000], str2[1000];
	cin>>str1>>str2;
	bign a = change(str1);
	bign b = change(str2);
	print(add(a, b));
	cout<<endl;
	print(sub(a, b));
	cout<<endl;
	print(divide(a, 4));
	cout<<endl;
	cout<<"余数："<<r<<endl; 
	print(mult(a, 11));
	return 0;
}

高精阶乘

#include<bits/stdc++.h>
using namespace std;

const int N = 1e4 + 10;
int a[N];
int index = 1;	//表示最大位所在的位置，初始为个位，在a[1]处 

int main() {
	int n;
	cin >> n;
	a[1] = 1;
	for (int i = 1; i <= n; i++) {
		int t = 0;	//进位的数 
		for (int j = 1; j <= index; j++) {
			a[j] = a[j] * i + t;
			t = a[j] / 10;
			a[j] = a[j] % 10;
		}
		while (t > 0) {	//进位 
			a[index + 1] = t % 10;
			t /= 10;
			index++;
		}
	}
	for (int i = index; i >= 1; i--) {
		cout << a[i];
	}
	return 0;
}

高精加法

a + b

#include<bits/stdc++.h>
using namespace std;

const int N = 1e4 + 10;
char a[N], b[N];
int p[N], q[N], res[N];

int main() {
	cin >> a >> b;
	int la = strlen(a);
	int lb = strlen(b);
	for (int i = 0; i < la; i++) {
		p[i] = a[la - i - 1] - '0';
	}
	for (int i = 0; i < lb; i++) {
		q[i] = b[lb - i - 1] - '0';
	}
	int len = max(la, lb);
	int t = 0;	//进位的数 
	for (int i = 0; i < len; i++) {
		res[i] = p[i] + q[i] + t;
		t = res[i] / 10;
		res[i] = res[i] % 10;
	}
	if (t == 1) cout << 1;
	for (int i = len - 1; i >= 0; i--) {
		cout << res[i];
	}
	return 0;
}

posted @ 2024-03-13 18:15 Liu-RC 阅读(32) 评论(0) 收藏举报

刷新页面返回顶部

猪头少年