浅谈回滚莫队

Luogu P5906 回滚莫队&不删除莫队

看题，考虑用莫队的写法来做。

我们发现，对于当前区间 \([l,r]\)，我们进行删除操作时很麻烦，不能直接得到，所以我们考虑用增加替换掉删除操作。

首先对序列分块。

对于要查询的区间在一个块里的，我们可以直接暴力搞出来

int cul(int l,int r){
  int res=0;
  for(int i=l;i<=r;i++){
    minnl[a[i]]=INF;
    maxxr[a[i]]=0;
  }
  for(int i=l;i<=r;i++){
    minnl[a[i]]=min(minnl[a[i]],i);
    maxxr[a[i]]=max(maxxr[a[i]],i);
    res=max(res,maxxr[a[i]]-minnl[a[i]]);
  }
  return res;
}

不在同一个块里呢？

先看回滚莫队的原理：

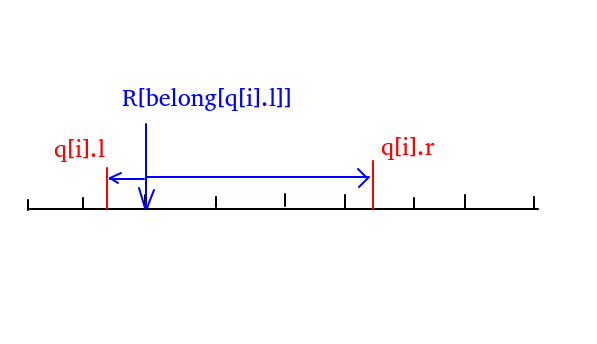
回滚莫队就是把起点设在要查询的区间的左端点块内的最右端，这样就避免了删除操作。

如果上一次查询的区间的左端点和这一次查询的区间的左端点在同一个块里呢？那是不是要再算一遍呢？显然不用，对于当前块的右端点，我们可以继续向右添加（因为要查询的块已经按右端点排好序了），对于当前块的左端点，我们要让她回到她这个块的最右端的位置，我们记下操作前的值，然后直接赋回原值就好了，这就是“删除”操作。

#include<bits/stdc++.h>
using namespace std;
inline int read(){
  int ans=0,f=1;char ch=getchar();
  while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
  while(isdigit(ch)){ans=(ans<<3)+(ans<<1)+ch-48;ch=getchar();}
  return ans*f;
}
const int N=2e5+5,INF=0x3f3f3f3f;
int n,block,m;
int a[N],b[N];
int rt1[N],rt2[N];
int lt1[N],lt2[N];
int maxx=0;
int belong[N],L[N],R[N];
struct lzz{
  int id,l,r;
}q[N];
bool cmp(lzz x,lzz y){
  if(belong[x.l]==belong[y.l]) return x.r<y.r;
  return belong[x.l]<belong[y.l];
}
void build(int x){
  block=sqrt(n);
  for(int i=1;i<=n;i++) belong[i]=(i-1)/block+1;
  int num=belong[n];
  for(int i=1;i<=num;i++){
    L[i]=R[i-1]+1;
    R[i]=min(n,L[i]+block-1);
  }
}
int ans[N];
void addr(int x){
  rt1[a[x]]=rt2[a[x]]=max(rt1[a[x]],x);
  lt1[a[x]]=lt2[a[x]]=min(lt1[a[x]],x);
  maxx=max(rt1[a[x]]-lt1[a[x]],maxx);
}
void addl(int x){
  rt1[a[x]]=max(rt1[a[x]],x);
  lt1[a[x]]=min(lt1[a[x]],x);
  maxx=max(rt1[a[x]]-lt1[a[x]],maxx);
}
void del(int x){
  rt1[a[x]]=rt2[a[x]];
  lt1[a[x]]=lt2[a[x]];
}
int minnl[N],maxxr[N];
int cul(int l,int r){
  int res=0;
  for(int i=l;i<=r;i++){
    minnl[a[i]]=INF;
    maxxr[a[i]]=0;
  }
  for(int i=l;i<=r;i++){
    minnl[a[i]]=min(minnl[a[i]],i);
    maxxr[a[i]]=max(maxxr[a[i]],i);
    res=max(res,maxxr[a[i]]-minnl[a[i]]);
  }
  return res;
}
int main(){
  n=read();
  for(int i=1;i<=n;i++) b[i]=a[i]=read();
  build(n);
  sort(b+1,b+1+n);
  int len=unique(b+1,b+1+n)-(b+1);
  for(int i=1;i<=n;i++){
    a[i]=lower_bound(b+1,b+1+len,a[i])-b;
  }
  m=read();
  for(int i=1;i<=m;i++) q[i].l=read(),q[i].r=read(),q[i].id=i;
  sort(q+1,q+1+m,cmp);
  int l=1,r=0;
  for(int i=1;i<=m;i++){
    if(belong[q[i-1].l]!=belong[q[i].l]){
      r=R[belong[q[i].l]];
      l=r+1;
      for(int j=1;j<=len;j++){
	rt1[j]=rt2[j]=0;
	lt1[j]=lt2[j]=INF;
      }
      maxx=0;
    }
    if(belong[q[i].l]==belong[q[i].r]){
      ans[q[i].id]=cul(q[i].l,q[i].r);
      continue;
    }
    while(r<q[i].r) addr(++r);
    int tmp=maxx;
    int tmpl=l;
    while(tmpl>q[i].l) addl(--tmpl);
    ans[q[i].id]=maxx;
    maxx=tmp;
    while(tmpl<l) del(tmpl++);
  }
  for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
  return 0;
}