浅谈线段树活用
SP1716 GSS3 - Can you answer these queries III
线段树求最大子段和
我们考虑对于每个区间维护四个值:sum、suml、sumr、res,分别存区间和、从左端点开始的最大子段和、从右端点开始的最大子段和、这个区间的最大子段和。
sum 的维护都会,对于 suml 和 sumr 有两种情况:
-
suml就等于左儿子的suml。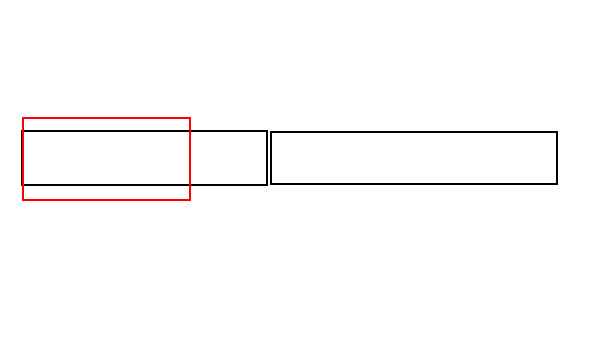
-
suml等于左儿子的区间和+右儿子的suml。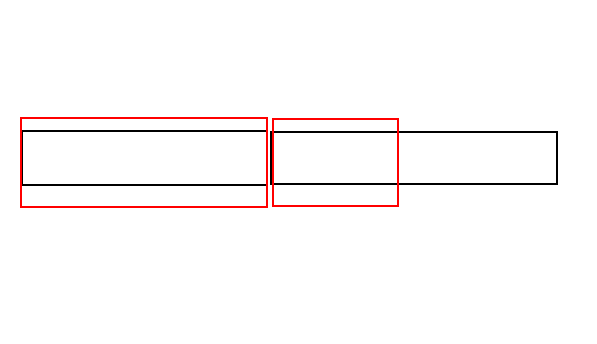
sumr 同理。对于所有情况取 \(max\) 即可。
有了这些东西怎么来得出答案呢?
答案分为三种情况:
-
res等于左儿子的res。 -
res等于右儿子的res。 -
res等于左儿子的sumr+ 右儿子的suml。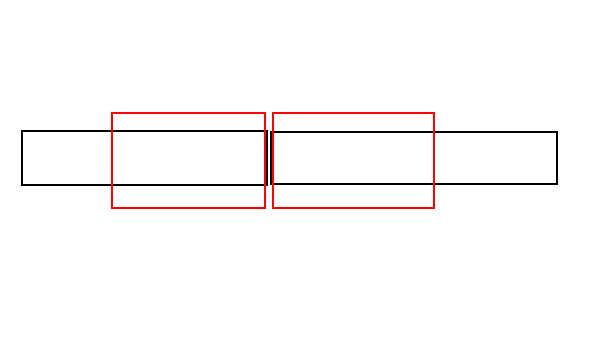
对于所有情况取 \(max\) 即可。
综上,我们解决了这题。
#include<bits/stdc++.h>
#define ls x<<1
#define rs x<<1|1
using namespace std;
inline int read(){
int ans=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
while(isdigit(ch)){ans=(ans<<3)+(ans<<1)+ch-48;ch=getchar();}
return ans*f;
}
const int N=5e4+5;
int n,Q;
int a[N];
struct QK{
int sum,suml,sumr,res;
}seg[N<<2];
void merge(int x){
seg[x].sum=seg[ls].sum+seg[rs].sum;
seg[x].suml=max(seg[ls].suml,seg[ls].sum+seg[rs].suml);
seg[x].sumr=max(seg[rs].sumr,seg[rs].sum+seg[ls].sumr);
seg[x].res=max(seg[ls].res,max(seg[rs].res,seg[ls].sumr+seg[rs].suml));
}
void build(int x,int l,int r){
if(l==r){
seg[x].sum=seg[x].suml=seg[x].sumr=seg[x].res=a[l];
return;
}
int mid=l+r>>1;
build(ls,l,mid);
build(rs,mid+1,r);
merge(x);
}
void update(int x,int l,int r,int p,int v){
if(l==r){seg[x].sum=seg[x].suml=seg[x].sumr=seg[x].res=v;return;}
int mid=l+r>>1;
if(p<=mid) update(ls,l,mid,p,v);
else update(rs,mid+1,r,p,v);
merge(x);
}
QK query(int x,int l,int r,int xl,int xr){
if(xl<=l&&xr>=r) return seg[x];
int mid=l+r>>1;
if(xr<=mid) return query(ls,l,mid,xl,xr);
if(xl>mid) return query(rs,mid+1,r,xl,xr);
QK res,tmpl=query(ls,l,mid,xl,xr),tmpr=query(rs,mid+1,r,xl,xr);
res.sum=tmpl.sum+tmpr.sum;
res.suml=max(tmpl.suml,tmpl.sum+tmpr.suml);
res.sumr=max(tmpr.sumr,tmpr.sum+tmpl.sumr);
res.res=max(tmpl.sumr+tmpr.suml,max(tmpl.res,tmpr.res));
return res;
}
int main(){
n=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
Q=read();
while(Q--){
int opt=read(),x=read(),y=read();
if(opt) printf("%d\n",query(1,1,n,x,y).res);
else update(1,1,n,x,y);
}
return 0;
}
SP6779 GSS7 - Can you answer these queries VII
高配版,移到了树上进行操作
我们只用树剖一下,然后按之前的做法维护即可。
注意下细节就可以了(调了1小时)。
#include<bits/stdc++.h>
#define ls x<<1
#define rs x<<1|1
using namespace std;
inline int read(){
int ans=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
while(isdigit(ch)){ans=(ans<<3)+(ans<<1)+ch-48;ch=getchar();}
return ans*f;
}
const int N=1e5+5;
struct QK{
int sum,suml,sumr,res,cov;
}seg[N<<2];
int lazy[N<<2];
int n,Q,a[N];
int hd[N],nx[N<<1],to[N<<1],tot;
void adde(int u,int v){
nx[++tot]=hd[u];to[tot]=v;hd[u]=tot;
nx[++tot]=hd[v];to[tot]=u;hd[v]=tot;
}
int fa[N],son[N],sz[N],dep[N];
void dfs1(int u,int father){
fa[u]=father;sz[u]=1;dep[u]=dep[father]+1;
for(int i=hd[u];i;i=nx[i]){
int v=to[i];
if(v==father) continue;
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>sz[son[u]]) son[u]=v;
}
}
int top[N],dfn[N],nfd[N],dfstime;
void dfs2(int u,int anc){
dfn[u]=++dfstime;top[u]=anc;nfd[dfstime]=u;
if(son[u]) dfs2(son[u],anc);
for(int i=hd[u];i;i=nx[i]){
int v=to[i];
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
void update(int x,int l,int r,int v){
seg[x].sum=v*(r-l+1);
seg[x].res=seg[x].sumr=seg[x].suml=max(0,seg[x].sum);
lazy[x]=v;seg[x].cov=1;
}
void pushdown(int x,int l,int r){
int mid=l+r>>1;
if(seg[x].cov){
update(ls,l,mid,lazy[x]);
update(rs,mid+1,r,lazy[x]);
lazy[x]=seg[x].cov=0;
}
}
void merge(QK &x,QK l,QK r){
x.sum=l.sum+r.sum;
x.suml=max(l.suml,l.sum+r.suml);
x.sumr=max(r.sumr,r.sum+l.sumr);
x.res=max(l.res,max(r.res,l.sumr+r.suml));
}
void update(int x,int l,int r,int xl,int xr,int v){
if(xl<=l&&xr>=r){
update(x,l,r,v);
return;
}
pushdown(x,l,r);
int mid=l+r>>1;
if(xl<=mid) update(ls,l,mid,xl,xr,v);
if(xr>mid) update(rs,mid+1,r,xl,xr,v);
merge(seg[x],seg[ls],seg[rs]);
}
void build(int x,int l,int r){
if(l==r){
seg[x].sum=a[nfd[l]];
seg[x].suml=seg[x].sumr=seg[x].res=max(0,seg[x].sum);
lazy[x]=0;
return;
}
int mid=l+r>>1;
build(ls,l,mid);
build(rs,mid+1,r);
merge(seg[x],seg[ls],seg[rs]);
}
QK query(int x,int l,int r,int xl,int xr){
if(xl<=l&&xr>=r) return seg[x];
pushdown(x,l,r);
int mid=l+r>>1;
if(xr<=mid) return query(ls,l,mid,xl,xr);
if(xl>mid) return query(rs,mid+1,r,xl,xr);
QK res;
merge(res,query(ls,l,mid,xl,xr),query(rs,mid+1,r,xl,xr));
return res;
}
void chainmodify(int x,int y,int v){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
update(1,1,n,dfn[top[x]],dfn[x],v);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
update(1,1,n,dfn[x],dfn[y],v);
}
void clear(QK &x){
x.sum=x.suml=x.sumr=x.res=0;
}
QK chainquery(int x,int y){
QK res,L,R;
clear(L);clear(R);clear(res);
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]){
merge(R,query(1,1,n,dfn[top[y]],dfn[y]),R);
y=fa[top[y]];
}
else{
merge(L,query(1,1,n,dfn[top[x]],dfn[x]),L);
x=fa[top[x]];
}
}
if(dep[x]>dep[y]) merge(L,query(1,1,n,dfn[y],dfn[x]),L);
else merge(R,query(1,1,n,dfn[x],dfn[y]),R);
swap(L.suml,L.sumr);
merge(res,L,R);
return res;
}
int main(){
n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<n;i++){
int x=read(),y=read();
adde(x,y);
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
Q=read();
while(Q--){
int opt=read(),x=read(),y=read();
if(opt==1) printf("%d\n",chainquery(x,y).res);
else chainmodify(x,y,read());
}
return 0;
}
[SHOI2008]堵塞的交通
线段树维护区间连通
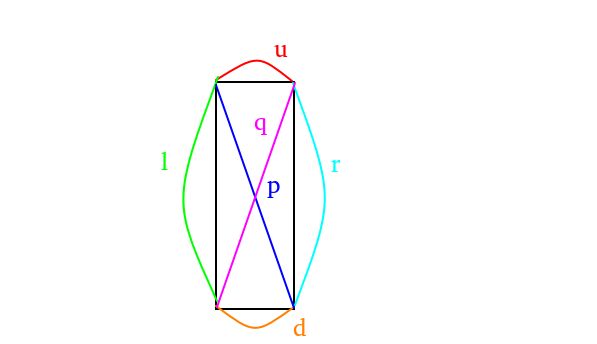
考虑维护每一列的区间连通性,以每一列为叶子节点建树,并定义以下变量:
- \(l\) 左上角到左下角是否连通
- \(r\) 右上角到右下角是否连通
- \(u\) 左上角到右上角是否连通
- \(d\) 左下角到右下角是否连通
- \(p\) 左上角到右下角是否连通
- \(q\) 左下角到右上角是否连通
- \(left\) 当前区间的左端点
- \(right\) 当前区间的右端点
如图:
同时,定义 \(con[i][0/1]\) 数组表示第 \(1/2\) 行的第 \(i\) 列和 \(i+1\) 列是否连通。
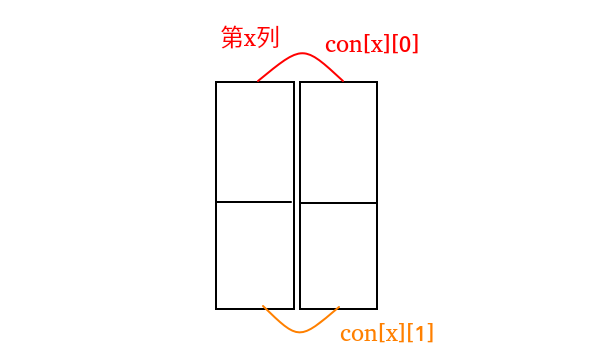
初始时,
对于叶子节点:
- \(l=r=1\)(自己到自己)
- \(u=d=p=q=0\)
对于所有节点,\(con[x][0/1]=0\)
考虑怎么合并两个区间的状态。(这里只考虑区间内的路径,对于区间外使区间连通的路径不考虑)
对于 \(l\) (\(r\) 同理)有红青两条路径。
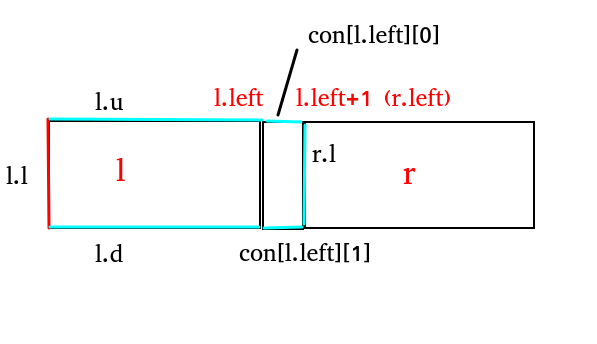
x.l=l.l|(l.u&con[l.right][0]&r.l&con[l.right][1]&l.d);
x.r=r.r|(r.u&con[l.right][0]&l.r&con[l.right][1]&r.d);
对于 \(u\)(\(d\) 同理)有红青两条路径。
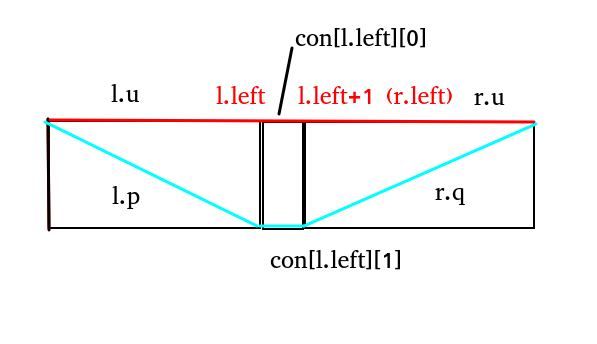
x.u=(l.u&con[l.right][0]&r.u)|(l.p&con[l.right][1]&r.q);
x.d=(l.d&con[l.right][1]&r.d)|(l.q&con[l.right][0]&r.p);
对于 \(p\) (\(q\) 同理)有红青两条路径。
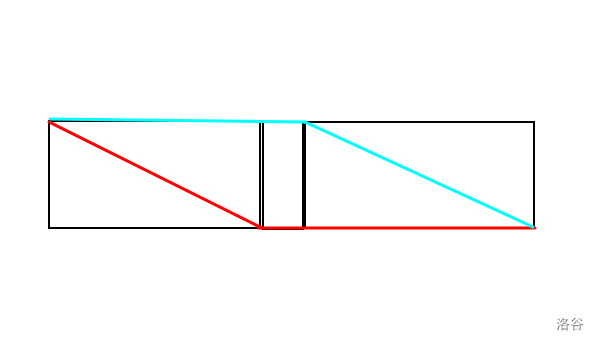
x.p=(l.p&con[l.right][1]&r.d)|(l.u&con[l.right][0]&r.p);
x.q=(l.q&con[l.right][0]&r.u)|(l.d&con[l.right][1]&r.q);
整个合并函数:
void merge(QK &x,QK l,QK r){
x.left=l.left;
x.right=r.right;
x.l=l.l|(l.u&con[l.right][0]&r.l&con[l.right][1]&l.d);
x.r=r.r|(r.u&con[l.right][0]&l.r&con[l.right][1]&r.d);
x.u=(l.u&con[l.right][0]&r.u)|(l.p&con[l.right][1]&r.q);
x.d=(l.d&con[l.right][1]&r.d)|(l.q&con[l.right][0]&r.p);
x.p=(l.p&con[l.right][1]&r.d)|(l.u&con[l.right][0]&r.p);
x.q=(l.q&con[l.right][0]&r.u)|(l.d&con[l.right][1]&r.q);
}
对于修改,我们分为同行修改和同列修改,同行修改改 \(con[x][0/1]\),同列修改改 \(l,r,q,p\)。同行修改改完后要合并一下。
void update1(int x,int l,int r,int p,int h,int val){
int mid=l+r>>1;
if(mid==p){
con[p][h]=val;
merge(seg[x],seg[ls],seg[rs]);
return;
}
if(mid>=p) update1(ls,l,mid,p,h,val);
else update1(rs,mid+1,r,p,h,val);
merge(seg[x],seg[ls],seg[rs]);
}
void update2(int x,int l,int r,int p,int val){
if(l==r){
seg[x].l=seg[x].r=seg[x].p=seg[x].q=val;
return;
}
int mid=l+r>>1;
if(mid>=p) update2(ls,l,mid,p,val);
else update2(rs,mid+1,r,p,val);
merge(seg[x],seg[ls],seg[rs]);
}
询问是正常的区间询问
QK query(int x,int l,int r,int xl,int xr){
if(xl<=l&&xr>=r) return seg[x];
int mid=l+r>>1;
if(mid<xl) return query(rs,mid+1,r,xl,xr);
if(mid>=xr) return query(ls,l,mid,xl,xr);
QK res=seg[x];
merge(res,query(ls,l,mid,xl,xr),query(rs,mid+1,r,xl,xr));
return res;
}
最后答案判断要分为 \([1,c1],[c1,c2],[c2,n]\) 三个区间来判断,像写 \(merge\) 函数一样大力讨论就好了。(画不动图了)
if(s[0]=='A'){
int flag=0;
QK L=query(1,1,n,1,c1),MID=query(1,1,n,c1,c2),R=query(1,1,n,c2,n);
if(r1==1&&r2==1) flag=MID.u|(L.r&MID.q)|(R.l&MID.p)|(L.r&MID.d&R.l);
if(r1==1&&r2==2) flag=MID.p|(L.r&MID.d)|(R.l&MID.u)|(L.r&MID.q&R.l);
if(r1==2&&r2==1) flag=MID.q|(L.r&MID.u)|(R.l&MID.d)|(L.r&MID.p&R.l);
if(r1==2&&r2==2) flag=MID.d|(L.r&MID.p)|(R.l&MID.q)|(L.r&MID.u&R.l);
printf(flag?"Y\n":"N\n");
}
代码:
#include<bits/stdc++.h>
#define ls x<<1
#define rs x<<1|1
using namespace std;
inline int read(){
int ans=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
while(isdigit(ch)){ans=(ans<<3)+(ans<<1)+ch-48;ch=getchar();}
return ans*f;
}
const int N=1e5+5;
struct QK{
int left,right;
int l,r,u,d,q,p;
}seg[N<<2];
int n;
int con[N][2];
void merge(QK &x,QK l,QK r){
x.left=l.left;
x.right=r.right;
x.l=l.l|(l.u&con[l.right][0]&r.l&con[l.right][1]&l.d);
x.r=r.r|(r.u&con[l.right][0]&l.r&con[l.right][1]&r.d);
x.u=(l.u&con[l.right][0]&r.u)|(l.p&con[l.right][1]&r.q);
x.d=(l.d&con[l.right][1]&r.d)|(l.q&con[l.right][0]&r.p);
x.p=(l.p&con[l.right][1]&r.d)|(l.u&con[l.right][0]&r.p);
x.q=(l.q&con[l.right][0]&r.u)|(l.d&con[l.right][1]&r.q);
}
void build(int x,int l,int r){
seg[x].left=l,seg[x].right=r;
if(l==r){
seg[x].u=seg[x].d=1;
return;
}
int mid=l+r>>1;
build(ls,l,mid);
build(rs,mid+1,r);
merge(seg[x],seg[ls],seg[rs]);
}
void update1(int x,int l,int r,int p,int h,int val){
int mid=l+r>>1;
if(mid==p){
con[p][h]=val;
merge(seg[x],seg[ls],seg[rs]);
return;
}
if(mid>=p) update1(ls,l,mid,p,h,val);
else update1(rs,mid+1,r,p,h,val);
merge(seg[x],seg[ls],seg[rs]);
}
void update2(int x,int l,int r,int p,int val){
if(l==r){
seg[x].l=seg[x].r=seg[x].p=seg[x].q=val;
return;
}
int mid=l+r>>1;
if(mid>=p) update2(ls,l,mid,p,val);
else update2(rs,mid+1,r,p,val);
merge(seg[x],seg[ls],seg[rs]);
}
QK query(int x,int l,int r,int xl,int xr){
if(xl<=l&&xr>=r) return seg[x];
int mid=l+r>>1;
if(mid<xl) return query(rs,mid+1,r,xl,xr);
if(mid>=xr) return query(ls,l,mid,xl,xr);
QK res=seg[x];
merge(res,query(ls,l,mid,xl,xr),query(rs,mid+1,r,xl,xr));
return res;
}
int main(){
n=read();
build(1,1,n);
while(1){
char s[N];
cin>>s;
if(s[0]=='E') break;
int r1=read(),c1=read(),r2=read(),c2=read();
if(c1>c2) swap(r1,r2),swap(c1,c2);
if(s[0]=='O'){
if(r1==r2) update1(1,1,n,c1,r1-1,1);
else update2(1,1,n,c1,1);
}
if(s[0]=='C'){
if(r1==r2) update1(1,1,n,c1,r1-1,0);
else update2(1,1,n,c1,0);
}
if(s[0]=='A'){
int flag=0;
QK L=query(1,1,n,1,c1),MID=query(1,1,n,c1,c2),R=query(1,1,n,c2,n);
if(r1==1&&r2==1) flag=MID.u|(L.r&MID.q)|(R.l&MID.p)|(L.r&MID.d&R.l);
if(r1==1&&r2==2) flag=MID.p|(L.r&MID.d)|(R.l&MID.u)|(L.r&MID.q&R.l);
if(r1==2&&r2==1) flag=MID.q|(L.r&MID.u)|(R.l&MID.d)|(L.r&MID.p&R.l);
if(r1==2&&r2==2) flag=MID.d|(L.r&MID.p)|(R.l&MID.q)|(L.r&MID.u&R.l);
printf(flag?"Y\n":"N\n");
}
}
return 0;
}
未完待续……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号