关于 DP 的一些内容
0.关于
动态规划是编程解题的一种重要手段。1951 年美国数学家 R.Bellman 等人,根据一类多阶段问题的特点,把多阶段决策问题变换为一系列互相联系的单阶段问题,然后逐个加以解决。与此同时,他提出了解决这类问题的“最优化原理”,从而创建了解决最优化问题的一种新方法:动态规划。
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。
我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
1.基本概念
· 阶段:把所给问题的求解过程恰当地分成若干个相互联系的阶段,以便于求解。过程不同,阶段数就可能不同。描述阶段的变量称为阶段变量,常用 k 表示。阶段的划分,一般是根据时间和空间的自然特征来划分,但要便于把问题的过程转化为多阶段决策的过程。
· 状态:状态表示每个阶段开始面临的自然状况或客观条件,它不以人们的主观意志为转移,也称为不可控因素。通常一个阶段有若干个状态,状态通常可以用一个或一组数来描述,称为状态变量。
· 决策:表示当过程处于某一阶段的某个状态时,可以做出不同的决定,从而确定下一阶段的状态,这种决定称为决策。不同的决策对应着不同的数值,描述决策的变量称决策变量。
· 状态转移方程:动态规划中本阶段的状态往往是上一阶段的状态和上一阶段的决策的结果,由第 i 段的状态 f(i) ,和决策 u(i) 来确定第 i+1 段的状态。状态转移表示为 F(i+1) = T(f(i),u(i)) ,称为状态转移方程。
· 策略:各个阶段决策确定后,整个问题的决策序列就构成了一个策略,对每个实际问题,可供选择的策略有一定范围,称为允许策略集合。允许策略集合中达到最优效果的策略称为最优策略。
动态规划必须满足最优化原理与无后效性。
· 最优化原理:“一个过程的最优决策具有这样的性质:即无论其初始状态和初始决策如何,其今后诸策略对以第一个决策所形成的状态作为初始状态的过程而言,必须构成最优策略”。也就是说一个最优策略的子策略,也是最优的。
· 无后效性:如果某阶段状态给定后,则在这个阶段以后过程的发展不受这个阶段以前各个状态的影响。
举个栗子
来看一道题目。
可怜的可乐机要回家,已知小可乐机在 左下角 (1,1) 位置,家在 右上角 (n,n) 坐标处。小可乐机走上一个格子 (i,j) 会花费一定的体力 a[i][j],而且小可乐机只会往家的方向走,也就是只能往上,或者往右走。小可乐机想知道他回到家需要花费的最少体力是多少, 求你帮帮小可乐机吧qwq
例如下图所示,格子中的数字代表走上该格子花费的体力:
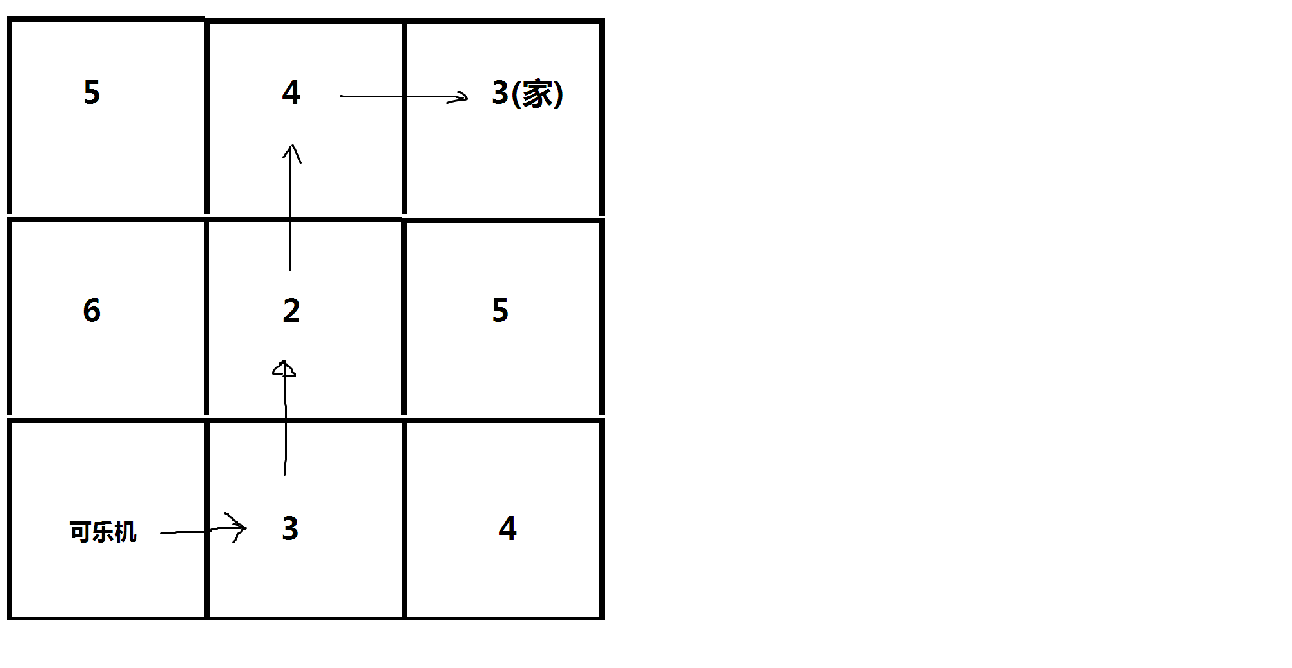
对于该图来说,最优策略已在图上标出,最少花费体力为:3 + 2 + 4 + 3 = 123 + 2 + 4 + 3 = 12。
我们把走到一个点看做一个状态,对小可乐机来说,走到一个点只有两种方式,一个是从下面走到该点,一种是从左边走到该点。那么点 (i,j) 要么是从 (i-1,j) 走到 (i,j),要么是从点 (i,j-1) 走到 (i,j)。
所以从哪个点走到 (i,j) 就是一个 决策。接下来,我们用 dp(i,j) 来代表走到点 (i,j) 一共花费的最少体力。
我们需要花费最少力气走到家,所以可以得到状态转移方程:dp(i,j) = min(dp(i-1,j), dp(i,j-1)) + a[i][j] 。根据转移方程,我们可以推出走到每个点花费的最少体力。
对于图中的边界点,要在转移前加上判断是否为边界,如:点 (1,3) 只能从点 (1,2) 走过来,点 (3,1) 只能从点 (2,1) 走过来等等。
动态规划的题目的核心是写出状态转移方程,对于一个动态规划的题目,如果我们能写出转移方程那么代码实现就变得简单多了。大部分的动态规划题目,在计算出转移方程后,可以用类似于递推的循环结构,来写出代码。
主要代码
int a[100][100]; // a数组代表在点(i,j)花费的体力
int dp[100][100]; // dp数组代表走到点(i,j)一共花费的最少体力
dp[1][1] = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (i == 1 && j == 1)
{
continue;
}
else if (i == 1) //边界点
{
dp[i][j] = dp[i][j-1] + a[i][j];
}
else if (j == 1) //边界点
{
dp[i][j] = dp[i-1][j] + a[i][j];
}
else
{
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + a[i][j]; //转移方程
}
}
}
01背包
01背包的主要思路是从后往前一次看当前这个物品选不选
那么有:
如果剩下的容量装不下这个物品:\(dp(i,j)=dp(i-1,j)\) (表示不选)
否则有 \(dp(i,j)=max(dp(i-1,j),dp(i-1,j-w_i)+v_i)\)
// 通过记忆化搜索实现的代码
#include <bits/stdc++.h>
#define MAXN 4005
#define MAXW 5005
using namespace std;
int n, W, w[MAXN], v[MAXN], dp[MAXN][MAXW];
int solve(int n, int W) // first n items. weight W
{
if(n == 0) // 如果没有物品了,那么就肯定得不到任何价值了,所以在这里return 0(边界条件)
return 0;
if(dp[n][W] != -1)
return dp[n][W];
if(W < w[n])
return solve(n - 1, W);
else
return max(solve(n - 1, W), solve(n - 1, W - w[n]) + V[n]);
}
int main()
{
memset(dp, -1, sizeof(dp));
scanf("%d %d", &n, &W);
for(int i = 1; i <= n; i++)
scanf("%d %d", &w[i], &v[i]);
printf("%d\n", solve(n, W));
return 0;
}
// 通过DP实现的代码
#include <bits/stdc++.h>
#define MAXN 4005
#define MAXW 5005
using namespace std;
int n, W, w[MAXN], v[MAXN], dp[MAXN][MAXW];
int main()
{
memset(dp, -1, sizeof(dp));
scanf("%d %d", &n, &W);
for(int i = 1; i <= n; i++)
scanf("%d %d", &w[i], &v[i]);
for(int i = 1; i <= n; i++)
for(int j = 0; j <= W; j++)
{
if(j < W[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]=max(dp[i-1][j]), dp([i-1][j-w[i]])+v[i]);
}
cout << dp[n][W] << endl;
return 0;
}
空间优化
我们仔细看这个01背包的递推式:
\(
dp[i][j]=
\left\{
\begin{array}{**lr**}
dp[i-1][j], & j<w[i]\\
max(dp[i-1][j], dp[i-1][j-w[i]]+v[i]) &
\end{array}
\right.
\)
可以发现dp[i][j]至于dp[i-1][多少多少]有关系,所以可以只用两行就可以存下来。
于是空间就只需要\(O(2*W)\)啦
#include <bits/stdc++.h>
#define MAXN 4005
#define MAXW 5005
using namespace std;
int n, W, w[MAXN], v[MAXN], dp[2][MAXW];
int main()
{
scanf("%d %d", &W, &n);
for(int i = 1; i <= n; i++)
scanf("%d %d", &w[i], &v[i]);
for(int i = 1; i <= n; i++)
for(int j = 0; j <= W; j++)
{
if(j < w[i])
dp[i%2][j]=dp[(i-1)%2][j];
else
dp[i%2][j]=max(dp[(i-1)%2][j], dp[(i-1)%2][j-w[i]]+v[i]);
}
cout << dp[n%2][W] << endl;
return 0;
}
最长不下降子序列
给你一个序列,让你求其中最长不下降子序列的长度[1];
仔细思考一下,我们想出来一个状态转移方程:
那代码就是这样写的啦:
#include <bits/stdc++.h>
using namespace std;
#define MAXN 10005
int a[MAXN], dp[MAXN];
int main()
{
memset(dp, 0, sizeof(dp));
int N;
scanf("%d", &N);
for(int i = 1; i <= N; i++)
scanf("%d", &a[i]);
for(int i = 1; i <= N; i++)
{
dp[i] = 1;
for(int j = 1; j < i; j++)
if(a[i] >= a[j])
dp[i] = max(dp[i], dp[j] + 1);
}
int ans = 0;
for(int i = 1; i <= N; i++)
ans = max(ans, dp[i]);
cout << ans << endl;
return 0;
}
一个序列,满足 \(a[i]>=a[j] \text{ }\text{ }\text{ }\text{ }\text{ } 1 \leq j \leq n\) ↩︎


 浙公网安备 33010602011771号
浙公网安备 33010602011771号