对角矩阵的压缩存储

对角矩阵即在矩阵A中，所有的非零元素都集中在以主对角线为中心的区域中。

由于对角矩阵的特殊性：对于矩阵元素a(i,j)!=0，|i-j|<=b。所以当半带宽为d时，则非零元素有(2*d+1)*n-(1+d)*d个。

非零元素中出现在主对角线上的(a(i,i),1<=i<=n)，当|i-j|>1时，元素a(i,j)=0。

由此可知一个k对角线矩阵(k为奇数)满足下述条件：

若|i-j|>(k-1)/2，则元素a(i,j)=0

若|i-j|<=(k-1)/2，则元素非0

将对角矩阵压缩存储

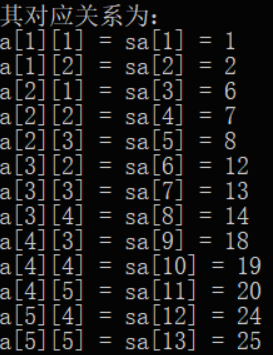
设一数组store[]有n*(2d+1)个元素来存储矩阵，元素store[k]与矩阵元素a[i,j]间有如下关系：store[1+(d-1)*(i-1)+j-1] = a(i,j)

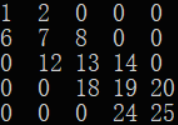
如下图这么一个矩阵