数值分析

目录

• 第 2 章
  • 多项式插值法
  • 拉格朗日插值法
  • 牛顿插值法
  • 埃尔米特插值法
• 第 3 章
  • 范数
  • 内积
• 第 8 章
  • 幂法与反幂法
  • 反幂法：
  • 豪斯霍尔德变换(Householder)
  • 吉文斯变换(Givens)
  • QR分解
  • QR方法

第 2 章

多项式插值法

拉格朗日插值法

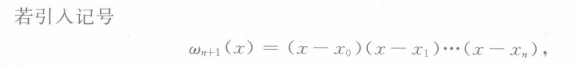
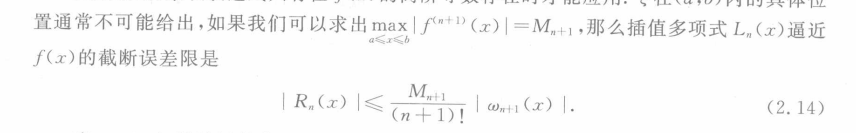
牛顿插值法

均差

插值公式

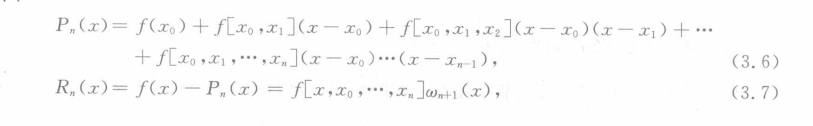
埃尔米特插值法

• 三点三次埃尔米特插值

给定三点信息和一点的导数值信息
利用牛顿插值多项式 + 导数值修正，使得得到的插值多项式满足上述两条件

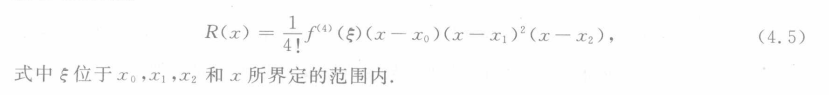
• 两点三次埃尔米特插值

给定两点及其导数信息
类似于拉格朗日插值多项式，构造函数开关使得对应位置在合适的时候取 1 或者 0
列式子好列，但是函数开关不好求，下面推导出来的公式尽可能的记住吧

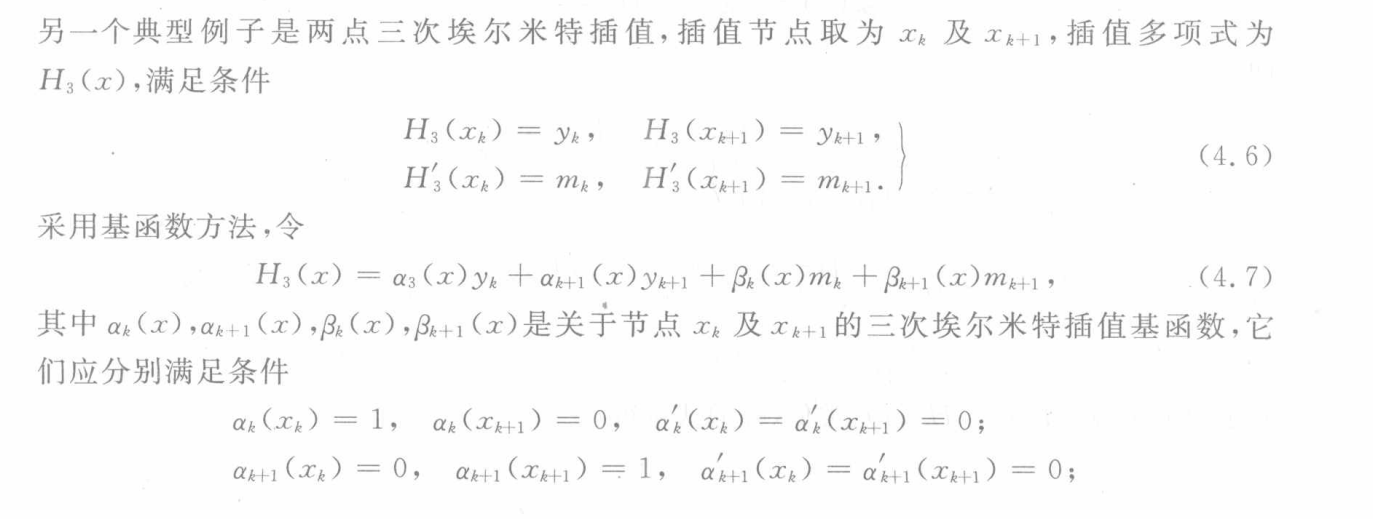
第 3 章

范数

内积

---

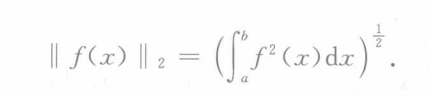
第 8 章

幂法与反幂法

规范后的幂法：书P248

$ u_k $ 表示迭代后的特征向量，$ \mu_k $ 表示特征向量

反幂法：

书P251

在近似值处求解：

书P253

$ u_k $ 表示特征向量，$ \lambda = \lambda_{近似} + \frac{1}{\mu} $

豪斯霍尔德变换(Householder)

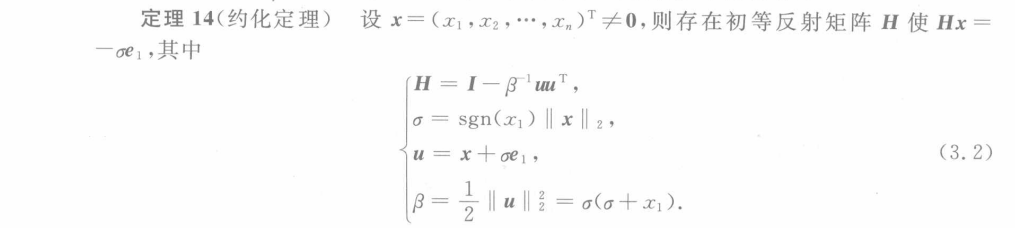
吉文斯变换(Givens)

书P257

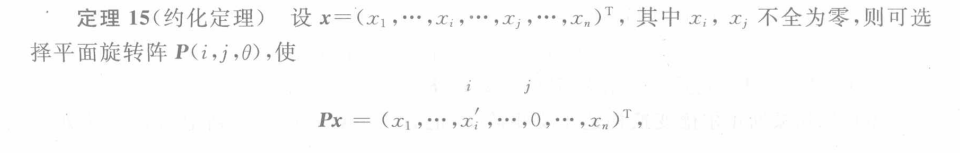
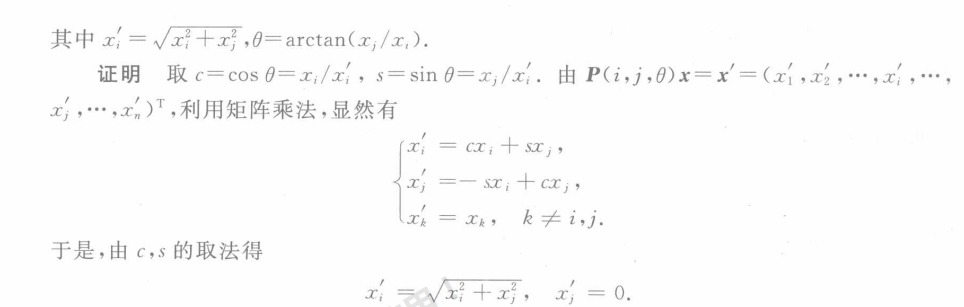
QR分解

书P258

QR方法