后缀自动机SAM
后缀自动机
好怪的东西,但是好像很牛的样子。刚听完视频,但是意犹未尽。
后缀自动机开 2n 空间
对于每一个节点,当前节点代表的后缀子串,长度最大的是len[p],最小的是len[p]-len[fa[p]]
节点字串数量len[p]-len[fa[p]]
后缀链有种后缀匹配的感觉
板子:
const int N = 1e5 + 5;
int tot = 1, np = 1;
int fa[N], ch[N][26], len[N], cnt[N];
void insert(int c){
int p = np;
np = ++tot;
len[np] = len[p] + 1;
cnt[np] = 1;
for(; p && !ch[p][c]; p = fa[p]) ch[p][c] = np;
if(p == 0) fa[np] = 1;// 1
else{
int q = ch[p][c];
if(len[q] == len[p]+1)// 2
fa[np] = q;
else{// 3
int nq = ++tot;
len[nq] = len[p] + 1;
fa[nq] = fa[q];
fa[q] = nq;
fa[np] = nq;
for(; p && ch[p][c] == q; p = fa[p]) ch[p][c] = nq;
memcpy(ch[nq], ch[q], sizeof(ch[q]));
}
}
return ;
}
具体过程:
仅以下面的模板题,说说后缀自动机插入一个字符时应当执行的操作:
p-回跳指针,np-新点,q链接点,nq新链接点
初始,tot=1,p=1
首先对于新输入的字符,肯定在上一次的最后插入一个新的位置,即 p = np; np = ++tot; np为新点的位置
之后更新这个新的点的最长串长度 len[np] = len[p] + 1; 和出现次数: cnt[p] = 1;
之后我们得为新点建边,为什么得全局建边呢?因为我们想节约空间,让前面的旧点利用这个新点。那为哪些点建边呢?因为考虑的是后缀,当后缀存在重复的情况,那么就可以均连在当前新点上。那么建边的语句就是:for(;p&&!ch[p][c];p=fa[p]) ch[p][c]=np; 已经处理了的fa指针就是最好的寻找目标,fa[i]指向i的上一层的节点
这一语句结束之后有三种情况会出现
1.p=0 说明当前这个边所代表的字符是新出现的字符,我们需要更新其的fa[np]=1
1.p!=0 说明这个边所代表的字符是早已出现过的字符
合法性: 子节点的最短串的最长后缀=父节点的最长串
对此,我们需要判断之前设置的点是否合法,令 q=ch[p][c]指向目前的p的下一层q
2.1 当len[q]=lne[p]+1时,合法。我们只需要更新 fa[np]=q;
2.2 当len[q]!=lne[p]+1时,不合法,我们需要复制出一个新的 q 节点 nq,之后更新相关信息。至于为啥要新建一个?因为之前建的那个不合法,具体见视频。
下为需要更新的信息的图片展示
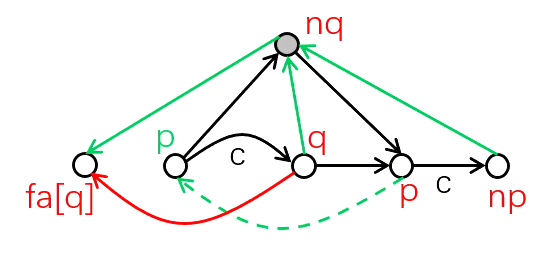
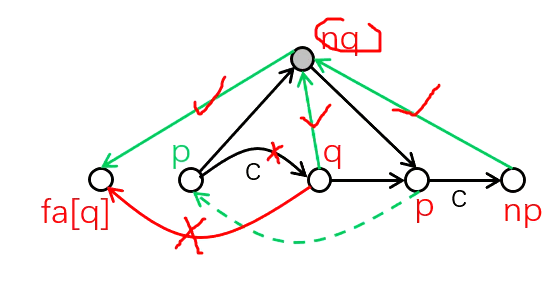
int nq=++tot;//nq是新链接点
len[nq]=len[p]+1;
//重建nq,q,np的链接边
fa[nq]=fa[q]; fa[q]=nq; fa[np]=nq;
//指向q的转移边改为指向nq
for(;p&&ch[p][c]==q;p=fa[p])ch[p][c]=nq;
//从q发出的转移边复制给nq
memcpy(ch[nq],ch[q],sizeof(ch[q]));
至此,当前节点的插入工作完成
例题
2023ACM暑假训练day 9 后缀自动机SAM
模板-子串出现次数
求子串出现次数大于1的子串的长度乘以次数的最大值
洛谷 P3804 【模板】后缀自动机(SAM)
下面的板子来源于董晓算法,强推其b站讲解
//邻接表写法
// Luogu P3804 【模板】后缀自动机 (SAM)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N=2e6+10;
char str[N];
vector<int> e[N];//邻接表
LL cnt[N],ans;
int tot=1,np=1;
//fa链接边终点,ch转移边终点,len最长串长度
int fa[N],ch[N][26],len[N];
void extend(int c){
//p回跳指针, np新点, q链接点, nq新链接点
int p=np; np=++tot;//p指向旧点, np是新点
len[np]=len[p]+1; cnt[np]=1;//子串出现次数
//p沿链接边回跳,从旧点向新点建转移边
for(;p&&!ch[p][c];p=fa[p]) ch[p][c]=np;
//1.如果c是新字符,从新点向根节点建链接边
if(p==0)fa[np]=1;
else{//如果c是旧字符
int q=ch[p][c];//q是链接点
//2.若链接点合法,从新点向q建链接边
if(len[q]==len[p]+1) fa[np]=q;
//3.若链接点不合法,则裂开q点,重建两类边
else{
int nq=++tot;//nq是新链接点
len[nq]=len[p]+1;
//重建nq,q,np的链接边
fa[nq]=fa[q]; fa[q]=nq; fa[np]=nq;
//指向q的转移边改为指向nq
for(;p&&ch[p][c]==q;p=fa[p]) ch[p][c]=nq;
//从q发出的转移边复制给nq
memcpy(ch[nq],ch[q],sizeof(ch[q]));
}
}
}
void dfs(int u){
for(auto v : e[u]){
dfs(v);
cnt[u]+=cnt[v];
}
if(cnt[u]>1)ans=max(ans,cnt[u]*len[u]);
}
int main(){
scanf("%s",str);
for(int i=0;str[i];i++) extend(str[i]-'a');
for(int i=2;i<=tot;i++) e[fa[i]].push_back(i);
dfs(1);
printf("%lld\n",ans);
return 0;
}
//链式前向星写法
// Luogu P3804 【模板】后缀自动机 (SAM)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N=2e6+10;
char str[N];
struct edge{int v,ne;}e[N];
int h[N],idx;//链式前向星
LL cnt[N],ans;
int tot=1,np=1;
//fa链接边终点,ch转移边终点,len最长串长度
int fa[N],ch[N][26],len[N];
void extend(int c){
//p回跳指针, np新点, q链接点, nq新链接点
int p=np; np=++tot;//p指向旧点, np是新点
len[np]=len[p]+1; cnt[np]=1;//子串出现次数
//p沿链接边回跳,从旧点向新点建转移边
for(;p&&!ch[p][c];p=fa[p])ch[p][c]=np;
//1.如果c是新字符,从新点向根节点建链接边
if(p==0)fa[np]=1;
else{//如果c是旧字符
int q=ch[p][c];//q是链接点
//2.若链接点合法,从新点向q建链接边
if(len[q]==len[p]+1)fa[np]=q;
//3.若链接点不合法,则裂开q点,重建两类边
else{
int nq=++tot;//nq是新链接点
len[nq]=len[p]+1;
//重建nq,q,np的链接边
fa[nq]=fa[q]; fa[q]=nq; fa[np]=nq;
//指向q的转移边改为指向nq
for(;p&&ch[p][c]==q;p=fa[p])ch[p][c]=nq;
//从q发出的转移边复制给nq
memcpy(ch[nq],ch[q],sizeof(ch[q]));
}
}
}
void add(int a,int b){
e[++idx]={b,h[a]};
h[a]=idx;
}
void dfs(int u){
for(int i=h[u];i;i=e[i].ne){
int v=e[i].v;
dfs(v);
cnt[u]+=cnt[v];
}
if(cnt[u]>1) ans=max(ans,cnt[u]*len[u]);
}
int main(){
scanf("%s",str);
for(int i=0;str[i];i++) extend(str[i]-'a');
for(int i=2;i<=tot;i++) add(fa[i],i);
dfs(1);
printf("%lld\n",ans);
return 0;
}
判断两个字符串的最长公共子串
见hdu提交,思路与下一题一样
2. Longest Common Substring
采用vjudge提交
这里利用了kmp算法的思想,对于一个字符串建后缀自动机,之后对于另一个字符串暴力匹配,利用fa指针回溯,同时统计一个匹配成功数equ,随时更新最大值。
//>>>Qiansui
#include<map>
#include<set>
#include<list>
#include<stack>
#include<cmath>
#include<queue>
#include<deque>
#include<cstdio>
#include<string>
#include<vector>
#include<utility>
#include<iomanip>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<functional>
#define ll long long
#define ull unsigned long long
#define mem(x,y) memset(x,y,sizeof(x))
#define debug(x) cout << #x << " = " << x << endl
#define debug2(x,y) cout << #x << " = " << x << " " << #y << " = "<< y << endl
//#define int long long
inline ll read()
{
ll x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-48;ch=getchar();}
return x*f;
}
using namespace std;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef pair<ull,ull> pull;
typedef pair<double,double> pdd;
/*
两个字符串的最大公共子串
*/
const int maxm=25e4+5,inf=0x3f3f3f3f,mod=998244353,N=maxm<<1;
ll ans=0,len[N];
int fa[N],ch[N][26],tot=1,np=1;
string s,t;
void insert(int c){
int p=np;
np=++tot;
len[np]=len[p]+1;
for(;p && !ch[p][c];p=fa[p]) ch[p][c]=np;
if(p==0) fa[np]=1;
else{
int q=ch[p][c];
if(len[q]==len[p]+1) fa[np]=q;
else{
int nq=++tot;
len[nq]=len[p]+1;
fa[nq]=fa[q];
fa[q]=nq;
fa[np]=nq;
for(;p && ch[p][c]==q;p=fa[p]) ch[p][c]=nq;
memcpy(ch[nq],ch[q],sizeof(ch[q]));
}
}
return ;
}
void solve(){
cin>>s>>t;
for(auto x:s) insert(x-'a');
ll p=1,c,equ=0;
for(int i=0;i<t.size();++i){
c=t[i]-'a';
if(ch[p][c]){
p=ch[p][c];
++equ;
}else{
while(p && !ch[p][c]) p=fa[p];
if(p){
equ=len[p]+1;
p=ch[p][c];
}else{
equ=0;p=1;
}
}
ans=max(ans,equ);
}
cout<<ans<<'\n';
return ;
}
signed main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
int _=1;
// cin>>_;
while(_--){
solve();
}
return 0;
}
相关资料
模板+视频讲解
学习主要来源
https://www.cnblogs.com/dx123/p/16151908.htm
杂
https://www.luogu.com.cn/blog/Kesdiael3/hou-zhui-zi-dong-ji-yang-xie


 浙公网安备 33010602011771号
浙公网安备 33010602011771号