NURBS__IFEM（1）

壳单元的应变推导

单元内任意一点的位移定义

单元的应变是由各单元结点位移在局部坐标自由度上的偏导，因此需要先表达壳体内任意一点的位移

变形前壳体内任意一点的位置： $$X(\theta^{1},\theta^{2},\theta^{3})=F(\theta^{1},\theta^{2})+\theta^{3}A_3(\theta^{1},\theta^{2}))$$ 变形后壳体内任意一点的位置： $$x(\theta^{1},\theta^{2},\theta^{3})=f(\theta^{1},\theta^{2})+\theta^{3}a_3(\theta^{1},\theta^{2}))$$

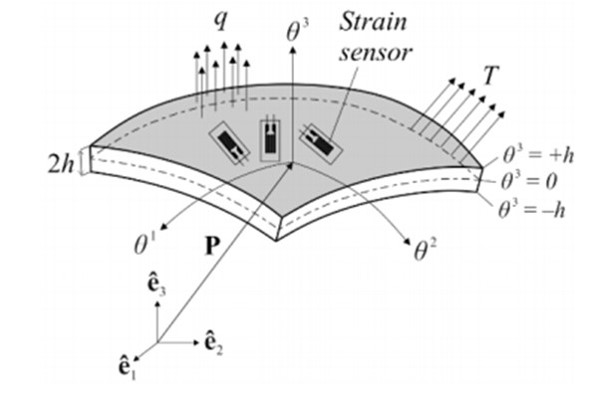
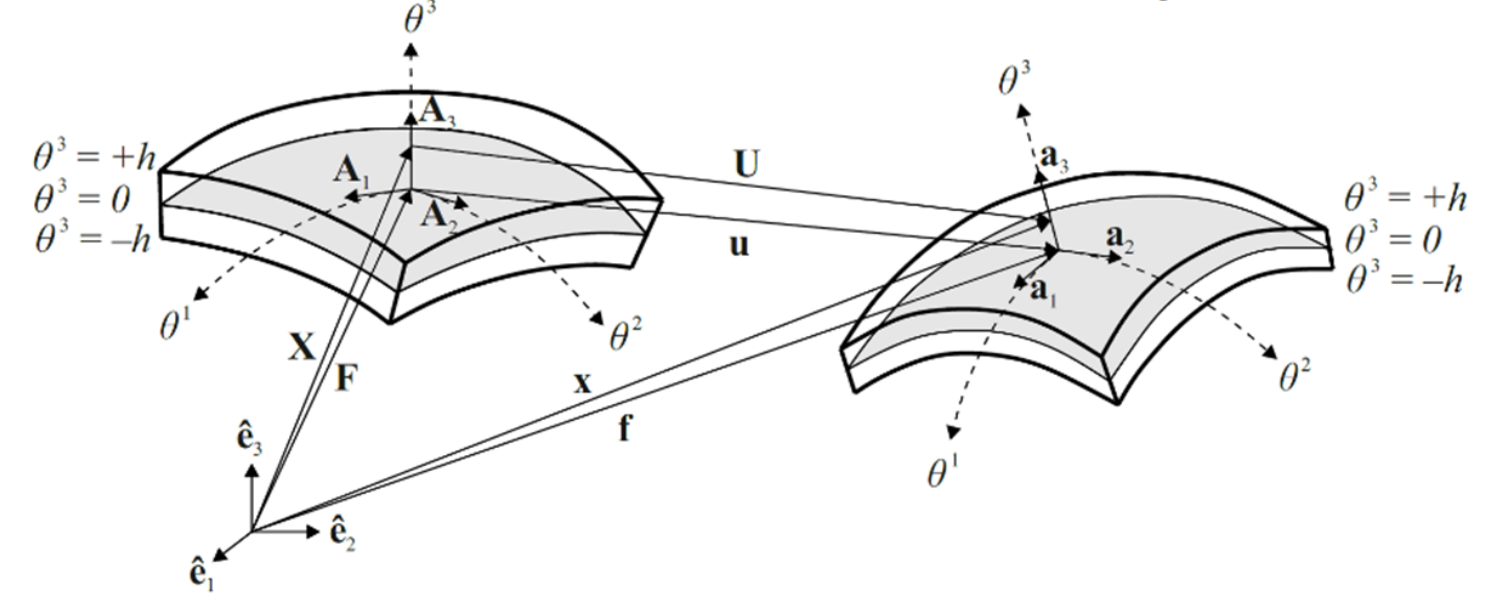
其中，\(f、F\)向量表示变形前后中面任意一点的位置，\(A_{\alpha}=F_{,\alpha}(\alpha=1,2)\),\(A_3=\frac{A_1\times A_2}{||A_1\times A_2||}\)

任意一点的位置可以由\(\theta_1,\theta_2,\theta_3\)表示，\(A_3\)向量可以由\(A_1和A_2\)的叉乘表示。

---

值得注意的是:

• \(A_{\alpha}\)是\(F_{\alpha}\)在等参坐标系坐标轴对应的偏导数;
• \(a_3=A_3+ \theta \times A_3\)
• 壳内任意一点的位移向量可以表示为：\(U=x-X=f-F+ \theta^3( \theta \times A_3)\)

显然\(f-F\)表示结点的直线位移，\(\theta^3( \theta \times A_3)\)表示转角位移。那么问题来了，这个\(a_3\)向量为什么这么表示？现已知旋转向量：

\[\theta=\chi_1 A_1+ \chi_2 A_2 \]

\(\chi_1\)和\(\chi_2\)表示对应\(A_\alpha\)的转动系数，注意是系数！不是角度！！ 不是角度！！！不是角度！！！！

---

假设\(a\)坐标系绕着\(A_2\)转动了\(k\)度，对应的转动系数应该是\(sin(k)\)，是因为\(k\)特别小，所以才无穷小成为一个度数，在几何意义上，我们其实是不能把他理解成一个度数来理解这个数学逻辑的。（类似于\(\displaystyle \lim_{x \to 0} sinx=x\)）

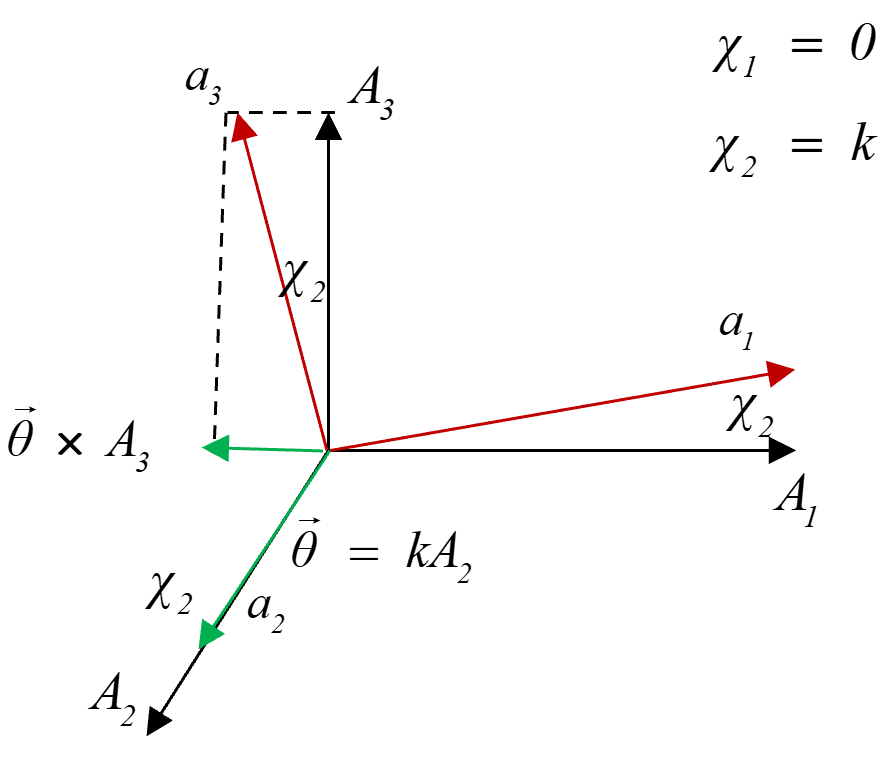
其实通过右图这个简单的例子，我们可以看到，在此情况下，变形后，厚度方向的向量\(a_3\)的表示确实如此。当\(\chi_1\)开始有值的时候，\(\theta \times A_3\)会在\(xy\)平面内顺时针或者逆时针转动。

\[\chi_1=\frac{(a_2-A_2)\bullet A_3}{||A_1\times A_2||}=\frac{u_{,2}\bullet A_3}{||A_1\times A_2||} \]

\[\chi_2=\frac{(a_1-A_1)\bullet A_3}{||A_1\times A_2||}=-\frac{u_{,1}\bullet A_3}{||A_1\times A_2||} \]

于是壳体内任意一点位移向量经过化解又有：

\[U=f-F+\theta^3 (\theta \times A_3)=u+\theta^3 (\theta \times A_3) \]

至此我们推导到出了壳体上，任意一点的位移的向量表示方法。

曲面任意一点的内应变表示

我们得到位移向量之后，根据应变的定义，只需要对等参数坐标系3个直线自由度方向求偏导，既\(\theta _1 ,\theta_2,\theta_3\),可以得到对应的应变表示。令，\((\bullet)_{,\alpha}= \frac{\partial (\bullet)}{\partial\theta^{\alpha}}\)

现在通过对\(U\)在\(\theta_1,\theta_2,\theta_3\)上求偏导获得应变表达，整体还是根据链式规则求偏导，需要注意的是：

1. 这里向量的之间的乘积方式，是点成还是叉乘要搞清楚。
2. 我们一定要注意U向量在图上是哪段,要注意，我们做最小二乘的时候，是在哪个坐标系下面进行的。
3. 求完偏导之后我们到的是一个应变向量，需要通过一组基函数获得在\(\theta_1,\theta_2,\theta_3\)上的分向量。（ps: 我在协变基这边理解了很长时间，之前以为是坐标变化，自己把自己推翻了。现在我觉得这个协变基的作用就是这样的。）
4. 待续！后面我加个例题，加深协变和逆变的理解

\[U_{,\alpha}=u_{,\alpha}+\theta_3(\theta_{,\alpha}\times A_3+\theta\times A_{3,\alpha}) \]

\[U_{,3}=\theta \times A_3 \]

我们需要在变形前局部坐标系\((\theta_1,\theta_2,\theta_3)\)下的表达应变，显然利用\(X_{,(\theta_1,\theta_2,\theta_3)}\)可以求出协基。

\[g_{\alpha}=X_{,\alpha}=A_{\alpha}+\theta^3A_{3,\alpha} \]

\[g_3=X_{,3}=A_3 \]

平面内的理论应力表达可以得到：

\[\begin{vmatrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \gamma_{12} \\ \end{vmatrix} = \begin{vmatrix} U_{,1}g_1\\ U_{,2}g_2\\ U_{,1}g_2+U_{,2}g_1\\ \end{vmatrix} = \begin{vmatrix} e_1 \\ e_2 \\ e_3 \\ \end{vmatrix} +\theta^3 \begin{vmatrix} \kappa_4 \\ \kappa_5 \\ \kappa_6 \\ \end{vmatrix} \]

在厚度方向的剪切应变，即\(\gamma_{13},\gamma_{23}\)可以表示为：

\[\gamma_{\alpha,3}=U_{,\alpha}\bullet g_3+U_{,3}\bullet g_{\alpha} \]

把这个式子展开，我们可以看到\(\gamma_{\alpha,3}\)为0

至此我们得到了壳体上任意一点的理论应变表达。就那\(xx,yy,xy\)三个，即：\(xy\)平面内的薄膜应变、弯曲应变和横向剪切。