曲线曲面基础

曲线曲面基础

隐式和参数表示

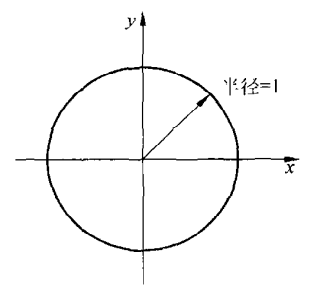
圆的归一化表示

对于一个圆心位于远点的单位圆周，可以由方程: \({f(x,y)=x^2+y^2-1=0}\) 来描述,见下图

在参数表示形式中，曲线上点的每个坐标分量均被表示为一个独立参数的显函数

$${ C(u)=(x(u),y(u)),a\leq u\leq b }$$

\({ C(u) }\)是一个独立变量u的矢值函数。区间\({ [a,b] }\)是任意的。于是，对上图的圆采用参数形式表示可以表示为：

$${ x(u)=cos(u)}$$ $${ y(u)=sin(u)}$$ $${ 0\leq u \leq \frac{\pi}{2}}$$

利用换元法，得到另一种等参表示：

$${ x(t)=\frac{1-t^2}{1+t^2}}$$ $${ y(t)=\frac{2t}{1+t^2}}$$ $${ 0\leq u \leq \frac{\pi}{2}}$$

复制格式

球的归一化处理

$${ x(u,v)=sin(u)cos(v)}$$ $${ y(u,v)=sin(u)sin(v)}$$ $${ z(u,v)=cos(u)}$$ $${0\leq u \leq 2\pi;0\leq v \leq \pi}$$

沿着经线和纬线的速度矢量，通过叉乘可以得到曲面上某点处的单位法式\({N}\):

\[{N=\frac{S_u×S_v}{|S_u×S_v|}} \]

曲面在一点处存在法矢和切平面是曲面的几何性质，和曲面的参数化没有关系。因此，尽管不同的参数化会产生不同的偏导矢量，但是只要法式的模不为零，那么N都是一样的。注意：在plor点，也就是极点的位置，即使没有速度偏导矢量，也是存在法式的，因此这个时候不能用叉乘的式子算。

幂基曲线

• 利用多项式逼近表示曲线的方法1
  一条\({n}\)次曲线的幂基表示形式是：

\[C(u)=(x(u),y(u),z(u))=\sum_{n}^{i=0}a_iu^{i},0\leq u\leq 1 \]

其中\({a=(x_i,y_i,z_i)}\)是矢量，因此\({x(u),y(u),z(u)}\)可以分别表示出来。注意到，这里我们用到的就是显函数的表达，\({u}\)可以看作是曲线上点向量与\({x}\)轴的夹角。写成矩阵：

\[{C(u)=\begin{vmatrix}a_0 & a_1 & ... & a_n \\\end{vmatrix} \begin{vmatrix} 1 \\ u\\ ...\\ u^{n}\\ \end{vmatrix}}\]

对\({C(u)}\)求导，

\[C^{i}(u)=\begin{vmatrix} a_1 & a_2 & ... & a_n \\ \end{vmatrix} \begin{vmatrix} 1 \\ 2u\\ 3u^2\\ ...\\ nu^{n-1} \end{vmatrix},i=1\]

显然，当对\(C(u)\)求\({n}\)阶导，可以得到：

\[{C^{n}=n!a_n} \]

其中\({a_n}\)就是幂基表示形式中的系数矢量。（解释：\({a_n}\)是关于某点的坐标矢量哦。）
若给定\({u_0}\),于是我们就有了：
当\({n=1}\):\({C(u_0)=au_0+a_0}\)
当\({n=2}\):\({C(u_0)=a_0+u_0(a_1+a_2u_0)}\)
当\({n=3}\):\({C(u_0)=a_0+u(a_1+u(a_2+a_3u))}\)
...

幂基函数的缺点：

• 形状不够自然，传递的几何特征很少。设计者需要指定两端的端点条件
• 处理次多项式的算法更多是代数风格，而不是几何。
• 数值计算上，不是好形式。此形式精度上会受舍入误差的影响。

Bezier贝塞尔曲线

• 利用多项式逼近表示曲线的方法2
  B方法克服了以上的缺点。一条\({n}\)次Bczicr曲线可以表示为：

\[{C(u)=\sum_{n}^{i=0}B_{i,n}(u)P_i,0\leq u\leq 1} \]

其中基函数就是著名的贝塞尔多项式,\({P}\)叫做控制点

\[{B_{i,n}(u)=\frac{n!}{i!(n-i)!}u^{i}(1-u)^{n-i}} \]

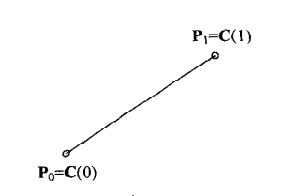
当\({n=1}\)时，\({B_{i,n}(u)=B_{0,1}P_0+B_{1,1}P_1}\)

其中：

\({B_{0,1}=1-u}\)

\({B_{1,1}=u}\)

因此：\({C(u)=(1-u)P_0+uP_1}\)

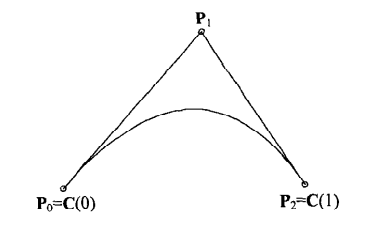
当\({n=2}\)时，\({B_{i,n}(u)=B_{0,2}P_0+B_{1,2}P_1+B_{2,2}P_2}\)

其中：

\({B_{0,2}=(1-u)^2}\)

\({B_{1,2}=2u(1-u)}\)

\({B_{2,2}=u^2}\)

因此：\({C(u)=(1-u)^2 P_0+2u(1-u)P_1+u^2P_2}\)

1. 由\(P_0,P_1,P_2\)组成的组成的多边形，称为控制多边形，很好的逼近了曲线的形状。
2. \({P_0=C(0),P_2=C(1)}\) 首尾都是以01为结尾
3. 曲线是包含在3点组成的三角形内的。

几何不变性：贝塞尔曲线进行变换时，只对控制点进行变化即可。（贝塞尔曲线属于B样条曲线的特例）

基函数的性质

1. 非负性：基函数和所有的\(i,n\)都是大于0的。
2. 规范性：换句话说就是值域和区间在\([0,1]\)
3. 端点性：第首尾个基函数的因变量分别对应为0，1
4. 最大值：在区间内只达到最大值一次
5. 对称性：关于\({u=1/2}\)对称。

贝塞尔方法相对于幂基的方法来说，贝塞尔形式的几何意义更强，前者更适合做曲线的交互设计。设计者通过控制点可以比幂基形式中的系数更直观的控制曲线形状。其缺点是计算效率差一点。

有理Bezier贝塞尔曲线

尽管多项式有很多优点，但是很多重要的曲线，曲面类型，如圆，椭圆，双曲线，圆柱面和圆锥面等等，无法精确地用多项式表达。例如：在\(xy\)平面内圆心在原点的单位圆周就无法用用多项式坐标函数精确的表示。证明采用反证法

由经典数学可知，包括圆在内的所有二次曲线，可以用有理函数（即：两个多项式相除）来表示

\[{x(u)=\frac{X(u)}{W(u)},y(u)=\frac{Y(u)}{W(u)}} \]

\(n\)次有理贝塞尔曲线的定义为：

\[{C(u)=\frac{\sum_{i=0}^{n}B_{i,n}w_i P_i}{\sum_{i=0}^{n}B_{i,n}w_i}} \]

其中\(w_i\)是权银子，\(\sum_{i=0}^{n}B_{i,n}\)是普通的标量函数。于是有：

\[{C(u)=\sum_{i=0}^{n}R_{i,n}(u)P_i} \]

\[{R_{i,n}(u)=\frac{w_iB_{i,n}(u)}{\sum_{i=0}^{n}B_{i,n}(u)w_i}} \]

其中\(R_{i,n}(u)\)是这种形式的曲线的有理基函数

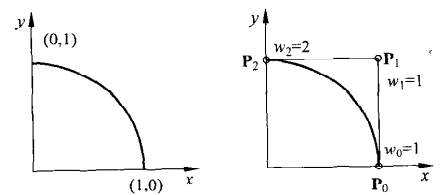
圆心在原点，半径为1的圆可以表示为：

\[{x(u)=\frac{1-u^2}{1+u^2}};y(u)=\frac{2u}{1+u^2} \]

\(C(u)=(x(u),y(u))\),现在推导二次有理贝塞尔表示其1/4圆弧。已知：

\({P_0=(0,0),P_1=(1,1),P_2=(0,1)}\)，求权因子。

\[{W(u)=1+u^2=\sum_{i=0}^{n}B_{i,2}(u)w_i}=C(u)=(1-u)^2 w_0+2u(1-u)w_1+u^2w_2 \]

令\(u=0\),得到\(w_0=1\)

令\(u=1\),得到\(w_1=2\)

令\(u=1/2\),得到\(w_2=1\)

到这里我就得到了他的权重。

二维空间的线，可以理解成为三维空间的线在二维空间的投影。于是我们利用齐次坐标，用\(n+1\)维空间中的多项式曲线来表达\({n}\)维空间中的一条有理数曲线。第\(n+1\)维度我们用权重来表示。
控制P于是有

\[P=H{P^{w}=H(X,Y,Z,W)=(\frac{X}{W},\frac{Y}{W},\frac{Z}{W})} \]

其中，点的方向为\((X,Y,Z)\)

---

问题回到圆弧中来，我们已知了二维空间中\(P_0,P_1,P_2\)的坐标以及权重\(w_0,w_1,w_2\)，于是我们的三维控制点：

\[P_{0}^{w}=w_0P_0=(1,0,1) \]

\[P_{1}^{w}=w_1P_1=(1,1,1), \]

\[P_{2}^{w}=w_2P_1=(0,2,2) \]

三维空间中非有理的抛物弧线，将其投影到二维平面上，即得所讨论的圆弧.

\[C^{W}(u)=(1-u)^2 P_{0}^{w}+2u(1-u)P_{1}^{w}+u^2 P_{2}^{w} \]

当\(u=1/2\)时:

\[C^{W}(1/2)=(1-u)^2 P_{0}^{w}+2u(1-u)P_{1}^{w}+u^2 P_{2}^{w}=(\frac{3}{4},1,\frac{5}{4}) \]

将其投影到到二维平面内，已知\(W=1+u^2=\frac{5}{4}\),（别忘了，炒个冷饭，这个就是有理曲线表达的的分母）即：

\[P=(\frac{3}{4}/W,\frac{5}{4}/W)=(\frac{3}{5},\frac{4}{5}) \]

接下来我们用其他形式来表示\(C(\frac{1}{2})\),验证一下对不对。使用已知的二维表达式

\[{x(u)=\frac{1-u^2}{1+u^2}};y(u)=\frac{2u}{1+u^2} \]

\[{C(1/2)=(x(1/2),y(1/2))=(\frac{3}{5},\frac{4}{5})} \]

证毕！

---

B样条基函数

仅由一段多项式或者有理多项式曲线段组成的曲线往往还是不能满足实际应用的要求，譬如：

1. 当需要满足约束条件很多时，需要使用高次曲线，例如，为了贝塞尔曲线通过\(n\)个数据，需要采用\(n-1\)次的曲线。但是，高次曲线用计算机处理时效率比较低，而且数值稳定性差
2. 为了精确拟合一些复杂的形状，需要采用高次曲线
3. 单独一段曲线或者曲面不适合交互形状设计。尽管通过控制顶点或者权重因子来改变有理贝塞尔形状，但是不具有局限性。

以上问题，可以通过分段多项式或者分段有理多项式表示的曲线或者曲面来解决。

这么一点文字，写了很久！还是不习惯这种编辑方式。
未完待续...，