"在线"卷积plus-从cdq分治到多叉与高维dft

"在线"卷积plus-从cdq分治到多叉与高维dft

假定与引入

不妨让我们呆在一个可以 \(O(1)\) 计算且便于 \(dft\) 的域上(如 \(F_{998244353}\))

半在线卷积形如

已知序列 \(\{f\}\), 求 \(\{fg\}\) 但 \(g_n\) 仅在 \((fg)_{n-1}\) 被计算出后才给出

全在线卷积形如

求 \(\{fg\}\) 但 \(f_n, g_n\) 仅在 \((fg)_{n-1}\) 被计算出后才给出

贡献图解

为了便于理解下面所讲解的内容, 这里先解释如何理解所谓的 "贡献图"

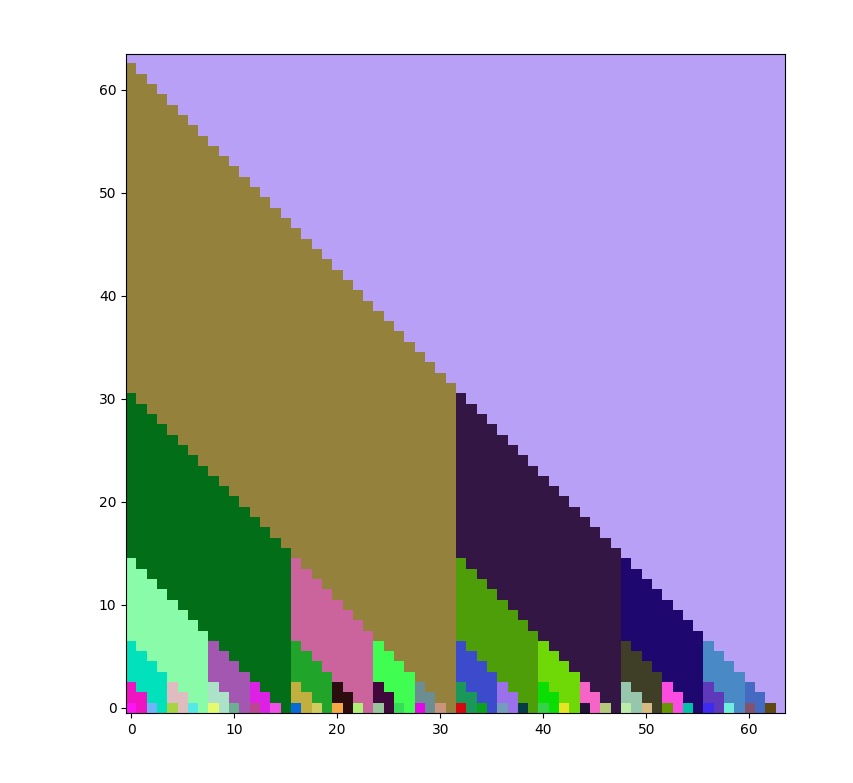
以长度为 8 的卷积图为例

此处应该有图

图上坐标为\((f_x,g_y)\) 的点对应 \(f_x \times g_y\), 卷积得到的 \((fg)_i\) 就是对斜线 \(x+y=i\) 求和.

那么我们的半在线计算过程就是

计算红色部分(\(x+y=0\))的和得到 \((fg)_0\) 进而得到 \(g_1\) 的值(如果是全在线此时才会得到 \(f_1\) 的值)

计算黄色部分(\(x+y=1\))的和得到 \((fg)_1\) 进而得到 \(g_2\) 的值(如果是全在线此时才会得到 \(f_2\) 的值)

计算浅绿色部分(\(x+y=2\))的和得到 \((fg)_2\) 进而得到 \(g_3\) 的值(如果是全在线此时才会得到 \(f_3\) 的值)

省略...

计算橙色(\(x+y=6\))的和得到 \((fg)_{6}\) 进而得到 \(g_{7}\) 的值(如果是全在线此时才会得到 \(f_{7}\) 的值)

计算米黄色(\(x+y=7\))的和得到 \((fg)_7\)

双向规约

半在线卷积和全在线卷积是容易双向规约的.

首先全在线卷积显然严格强于半在线卷积, 因此我们的问题实际上就是全在线卷积如何归约到半在线卷积

可以考虑一个倍增的思路, 检查其贡献形式.

此处应该有图

我们的计算过程就是, 考虑先计算出红色部分全在线卷积的答案, 然后易于用一次卷积计算橙色部分的贡献，紫色部分的贡献就可以看成两个(\(f\) 前半部分已知算 \(g\) 后半部分和 \(g\) 前半部分已知算 \(f\) 后半部分,这两个需要同步进行的)半在线卷积, 计算完后得到了浅绿色边框框住的全在线卷积的答案, 然后可以再用同样的方式加倍.

由图可以发现, 不妨设全在线卷积复杂度为 \(T_l\), 半在线卷积复杂度为 \(T_s\)

可以规约为 \(T_l(n) = T_l(n/2) + O(n\log n) + 2T_s(n/2)\)

显然半在线卷积不会弱于卷积, 所以我们不妨假设其复杂度 \(T_s(n)\ge O(n\log n), T_s(n) \ge 2T_s(n/2)\)

故原式可以写为 \(T_l(n) = T_l(n/2) + T_s(n)\) 显然这不会超过 \(2T_s(n)\) 故这两个东西同阶, 如果半在线卷积能以 \(T(n)\) 的复杂度解决则全在线卷积同样可以.

因此下面主要讲半在线卷积如何做.

cdq分治

拆成两段, 先算左边, 然后算左对右的贡献, 然后算右边.

其贡献图解也就是

此处应该有图

其中每种颜色代表一次卷积产生的贡献.

其复杂度为 \(T(n)=2T(n/2)+O(n\log n)\)

解得 \(T(n)=O(n\log^{2}n)\)

值得注意的是, 使用 \(dft\) 的乘法是循环卷积, 而我们注意到我们贡献的形式是长 \(2n\) 的序列卷上长 \(n\) 的序列然后提取后半部分, 那我们的 \(dft\) 长度只需要做到 \(2n\) 因为溢出的部分我们正好不要, 这对之后的做法至关重要.

此处应该有图

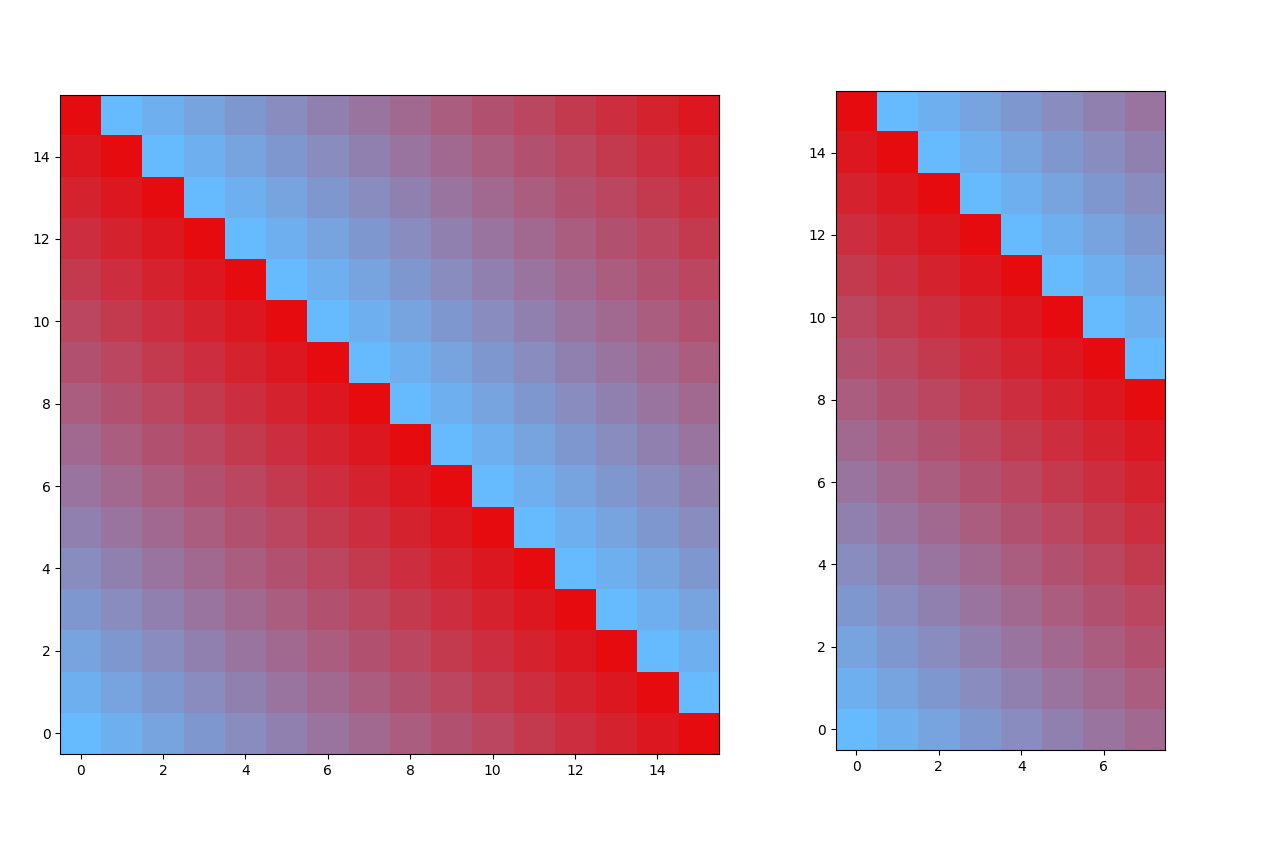
如图,左图是 \(16\times16\) 的完整循环卷积,右图是由于后半部分为 \(0\) 删去留下的 \(16\times8\) 贡献图, 其中颜色相同的块在循环卷积中贡献到同一部分.

对于截断卷积(以及正常卷积)而言, 为了使溢出不破坏结果, 必须把贡献限制在左下角的三角形中(蓝到红第一次渐变的部分), 但实际的贡献是一个矩形(最难处理右上角), 因此 \(dft\) 的长度必须超过两个多项式的 \(\deg\) 之和.

多叉分治

能不能再给力一点啊?

我们注意到 \(dft\) 之后的点值形式容易计算之间的贡献, 只要最后 \(idft\) 就好了.

考虑拆成 \(B\) 段, 每次计算前面的段对本段的贡献, 然后算本段, 不难发现这样我们会做 \(O(B)\) 次长度为 \(O(n/B)\) 的 \(dft\) 和 \(idft\) 以及 \(O(B^2)\) 次长度为 \(O(n/B)\) 的点乘.

其贡献图解也就是

此处应该有图

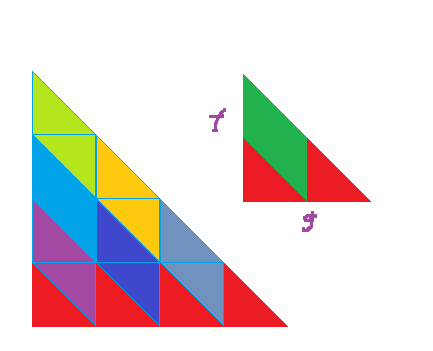
其中左下部分是四叉分治, 右上是正常二叉分治(作为对比), 红色三角即为向下分治, 每种颜色(除红色)代表一次 \(dot\) 所积累的贡献

(更具体的, 参考图解, 一般来说是 \(2B-2\) 次长度 \(2n/B\) 的 \(dft\) 以及其一半次数的 \(idft\) 以及 \(\dfrac{B(B-1)}{2}\) 次长度为 \(2n/B\) 的点乘)

因此复杂度为 \(T(n)=BT(n/B)+O(nB)+O(n\log n)\)

解得 \(B=O(\log n)\) (根据某人的说法最好取大一点因为 \(dft\) 一般比 \(\frac{1}{2}\log n\) 次 \(dot\) 慢)此时有 \(T(n)=O(\dfrac{n\log^2n}{\log \log n})\)

递归结构

能不能再给力一点啊?

回顾上一张图, 我们惊奇的发现块之间的贡献同样是一个半在线卷积的形式/惊奇/惊奇/惊奇

那么块之间的贡献我们可以同样用一个半在线卷积跑, 这是一个递归的结构, 有点类似区间静态半群查询.

这里的跑的块是 \(dft\) 之后的点值, 因为这样之间的乘法才能做到 \(O(len)\)

另一个理解的视角就是这是高维 \(dft\).

考虑到我们在 cdq 部分提及的循环卷积问题, 这部分每块的长度就是 \(2n/B\)

复杂度是 \(T(n)=BT(n/B)+(2n/B)T(B)+O(n\log n)\) .

一个可能的平衡是取 \(B=\sqrt n\) 这样就有 \(T(n) = 3T(\sqrt n)+O(n \log n)\), 解得 \(T(n) = O(n\log^{\frac{log 3}{log 2}}n)\)

此时 \(dft\) 的维度(最大)是 \(O(\log \log n)\) 维.

能不能再给力一点啊?

显然原式两支并不平衡, 所以我们可以直接在这个式子上做的更好.

令 \(l=\log_2 n\), \(H(l)=T(n)/n\) ,则有 \(H(n)=H(n-b)+2H(b)+O(n)\)

这个式子可以 dp 求最小转移点, 不过我们还是稍微推一下看看到底长什么样.(感谢 kyee 和热心 u群群友.)

令 \(a=\frac{n}{b}\)

\(H(n) \le \sum_{i=0}^{a} (2H(b)+O(n))\)

\(H(n) \le 2aH(n/a) + O(na)\)

不妨令 \(n=2^{\frac{k(k+1)}{2}+r}\), 其中 \(r\le k+1\)

则取 \(a=2^k\) ,令 \(P(k)=H(2^{\frac{k(k+1)}{2}})\)

有 \(P(k)=2^{k+1}P(k-1)+O(2^\frac{k(k+3)}{2})\)

解得 \(P(k)=O(k2^{\frac{(k+1)(k+2)}{2}})\) 这一点容易通过归纳法验证.

\(r\) 部分容易通过一次分治处理, 我们有

\(H(n)=2^{r+1}P(k)+O(2^{\frac{k(k+1)}{2}+r+r})\)

\(H(n)=O(k2^{\frac{k(k+1)}{2}+r+(k+2)})=O(n2^{\sqrt{2\log_2n}}{\sqrt{\log_2{n}}})\)

那么原式复杂度不会高于 \(T(n)=nH(log_2 n)=O(n\log n2^{\sqrt{2\log_2\log_2n}}\sqrt{\log \log n})\)

其他参考资料

https://www.cnblogs.com/Elegia/p/vDH07-relaxed-multiplication.html (EI blog)

https://hly1204.blog.uoj.ac/blog/7319 (hly1204 blog)

https://judge.yosupo.jp/submission/304264 (一份对 \(O(n\log n2^{\sqrt{2\log_2\log_2n}}\sqrt{\log \log n})\) 半在线卷积的实现)