树链剖分——(难度终于下来了|码量略大
这个东西——真 的 不 难!
(要不是太困了这玩意早学完了
板子:
代码见提交页。
注意:树剖求LCA复杂度为 \(O(n \log n)\),再套线段树复杂度为 \(O(n \log^2 n)\)。
主要题型:
树链剖分主要是将 树上区间问题,转化为能用 线段树 解决的问题。
-
点权改边权
-
树剖求LCA
-
线段树的更多复杂操作(难点在线段树
-
换根
警钟敲烂:
- 在修改的时候一定要将输入序改为dfs序!!!
典例:
1. 将点权改边权:
代码见提交页。
主要思想:将每条边的边权转化为当前边深度较深的端点上,在区间操作的时候将:
query(1,id[x],id[y]);
改为:
query(1,id[x]+1,id[y]);
2.树剖还可以求 LCA 哦!
时间复杂度 \(O(\log n)\)。
主要操作就是我们将两个点不断地跳 \(top\)。
实际上在 树剖模板 和其他大多数 树剖套线段树 中,树上两点之间操作就是逐步向上跳到两点 LCA 的时候顺便进行区间操作罢了。
其实这道题树上倍增+LCA也可,用树剖主要是求 LCA(其实大可不必。
3. 巧妙转化:
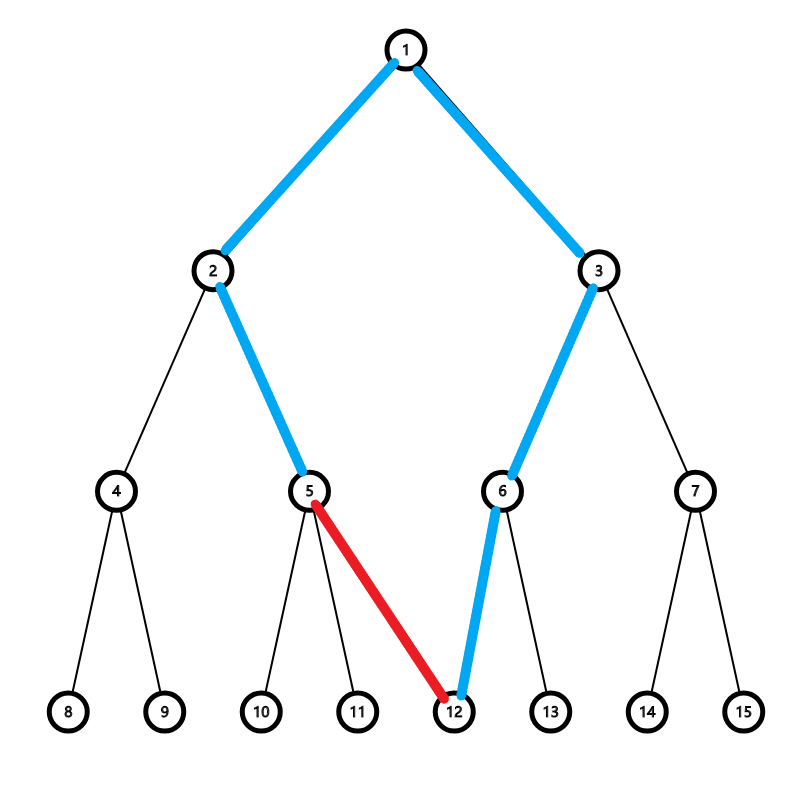
要想让新边 \(E(u,v)\) 生效,必须要割掉一些边。需要割掉的边就是 \(u\) 到 \(v\) 路径上的任意一条边,如下图如所示:
4. 树上染色问题:
维护该【区间颜色段数】,【区间左端点颜色】,【区间右端点颜色】。
接下来便是细节:
push_up 的时候需要加入:
if (tree[u*2].rc==tree[u*2+1].lc) tree[u].w--;
在树上区间询问向上跳的时候考虑维护两个变量:\(lpos\) 和 \(rpos\) 分别代表两点 \(x\) 和 \(y\)(这里认为 \(dep[x]>dep[y]\))向上跳时的起点。
同时在线段树询问操作时维护当前询问区间左端点颜色和右端点颜色:
if (l<=tree[u].l&&r>=tree[u].r) {
if (l==tree[u].l) LC=tree[u].lc;
if (r==tree[u].r) RC=tree[u].rc;
return tree[u].w;
}
接下来在 \(x\) 向上跳的过程中利用我们刚才维护的变量进行去重:
inline ll tree_sum(ll x,ll y) {
ll ans=0;
ll lpos=0,rpos=0;//
while (top[x]!=top[y]) {
if (dep[top[x]]<dep[top[y]]) swap(x,y),swap(lpos,rpos);//
ans=(ans+query(1,id[top[x]],id[x]));
if (RC==lpos) ans--;
lpos=LC;
x=fa[top[x]];
}
if (dep[x]>dep[y]) swap(x,y),swap(lpos,rpos);
ans+=query(1,id[x],id[y]);
if (lpos==LC) ans--;//
if (rpos==RC) ans--;//
return ans;
}
代码后面加斜杠的代表去重操作。
5. 线段树维护区间 从左到右/从右到左 极差
考虑维护区间【最大值】和【最小值】以便维护区间 【从左到右】/【从右到左】 极差:
push_up 操作:
st[root].maxx=max(st[root*2].maxx,st[root*2+1].maxx);
st[root].minn=min(st[root*2].minn,st[root*2+1].minn);
st[root].lmax=max(max(st[root*2].lmax,st[root*2+1].lmax),st[root*2+1].maxx-st[root*2].minn);
st[root].rmax=max(max(st[root*2].rmax,st[root*2+1].rmax),st[root*2].maxx-st[root*2+1].minn);
push_down 操作:
inline void push_down(int root){
int k=st[root].tag;
st[root].tag=0;
st[root*2].maxx+=k;
st[root*2].minn+=k;
st[root*2+1].maxx+=k;
st[root*2+1].minn+=k;
st[root*2].tag+=k;
st[root*2+1].tag+=k;
}
需要线段树合并操作,否则:
不用线段树合并操作分类讨论极为毒瘤
6. 树链剖分在无修改时改离线
小技巧:观察到只有查询操作,无修改操作,考虑离线!
先离线,然后根据询问的颜色大小由大到小排序,维护区间最大颜色值,该大小颜色全部查询完毕之后,将该颜色在线段树上修改为极小值。
7. 换根树剖
主要解决【修改/查询】以某点为根的子树的问题。
我们先以 \(1\) 结点为根进行树剖操作。
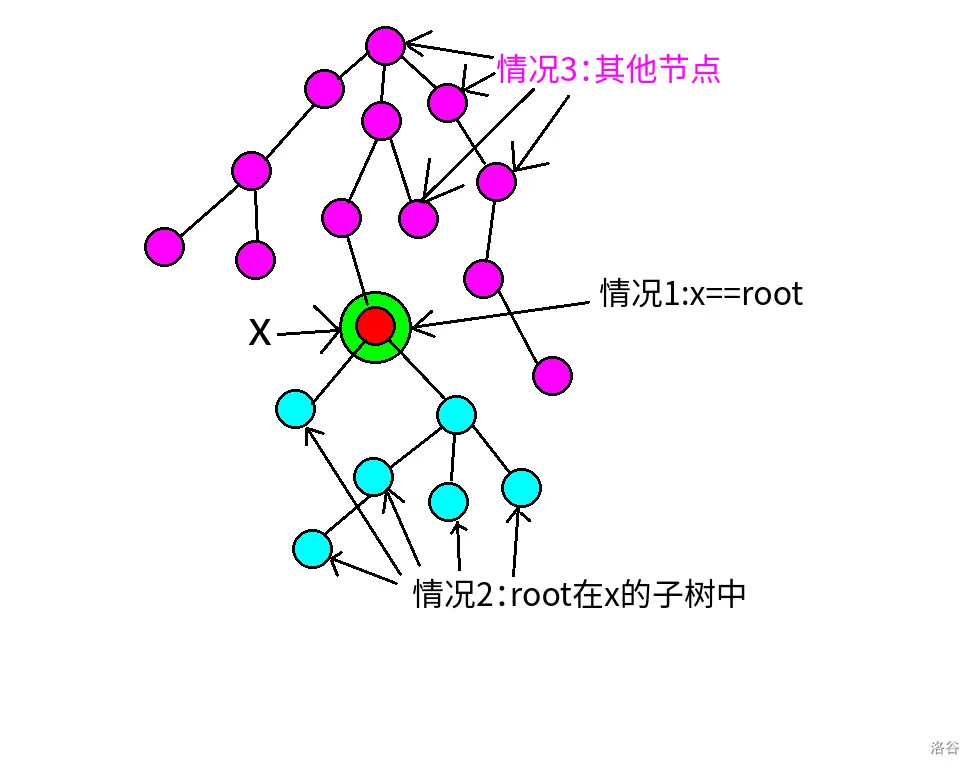
接下来分三种情况考虑:
- 当前要询问的节点就是当前根:
查询值就是区间最小值。
- 询问点是当前根的祖先:
查询值为 整棵树的权值 除去 根方向的子树
- 剩下的情况(当前与根无关):
正常操作即可
情况如下所示:
对应到代码上就是:
inline ll lcason(ll x,ll y) {
while (top[x]!=top[y]) {
if (dep[top[x]]<dep[top[y]]) swap(x,y);
if (fa[top[x]]==y) return top[x];//root在以x为根的子树的轻链中情况
x=fa[top[x]];
}
if (dep[x]>dep[y]) swap(x,y);
return son[x];
}
inline ll tree_min(ll x) {
ll temp=lcason(x,root);
if (x==root) return tree[1].w;
else if (dep[x]<dep[root]&&fa[temp]==x) return min(query(1,1,id[temp]-1),query(1,id[temp]+siz[temp],n));//跳过 root 方向子树部分
else return query(1,id[x],id[x]+siz[x]-1);
}
比上一道题多的就是求 LCA。
方法:
-
如果 \(x,y\) 都在 \(root\) 的子树内,那么 \(\texttt{LCA}\) 显然为 \(\texttt{LCA}(x,y)\)。
-
如果 \(x,y\) 只有一个在 \(r\) 的子树内,那么 \(\texttt{LCA}\) 肯定为 \(r\)。
-
如果 \(x,y\) 都不在 \(r\) 的子树内,我们可以先找到 \(p=\texttt{LCA}(x,r)\),\(q=\texttt{LCA}(y,r)\)。如果 \(p\) 和 \(q\) 不相同,那么我们选择其中较深的一个;如果 \(p\) 和 \(q\) 相同,那么 \(\texttt{LCA}\) 就是 \(p\) 或 \(q\)。
综上所述,我们可以发现我们要求的 \(\texttt{LCA}\) 就是 \(\texttt{LCA}(x,y)\),\(\texttt{LCA}(x,r)\),\(\texttt{LCA}(y,r)\) 这三者中深度最大的!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号