【网络流（瘤）】——用普及的代码诠释着的noi级的难度

前言：原本以为这个算法应该和二分图难度差不多（哎不就是一个 dfs + 一个 bfs 吗，就这？），结果难度远超人想象。

上次本人在【二分图】笔记中说到这（二分图）可能是写过的最详尽的笔记了，这不？更详尽的来了。

以下【算法内容】按难度升序排列

难点主要在于算法的理解和建模，建模才是最重要的。

最大流：

最常用算法：dinic

对于 dinic 算法讲解的比较好的博客：

洛谷日报 ||题解1号||视频一号||视频2号

接下来代码中 dinic 时间复杂度为 $O(n^2m)$。

模板：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inf 0x7fffffff
const ll maxn=500010;
ll n,m,s,t,cnt=1,ans;
ll head[maxn],dis[maxn],now[maxn];
struct edge {ll to,next,w;}e[maxn];
inline void add(ll u,ll v,ll w) {
	e[++cnt].w=w;
	e[cnt].to=v;
	e[cnt].next=head[u];
	head[u]=cnt;
	e[++cnt].w=0;
	e[cnt].to=u;
	e[cnt].next=head[v];
	head[v]=cnt;
}
inline ll bfs() {  
	for(register int i=1;i<=n;i++) dis[i]=inf;
	queue<int> q;
	q.push(s);
	dis[s]=0;
	now[s]=head[s];
	while(!q.empty()) {
		int x=q.front();
		q.pop();
		for(register int i=head[x];i;i=e[i].next) {
			int v=e[i].to;
			if(e[i].w>0&&dis[v]==inf) {
				q.push(v);
				now[v]=head[v];
				dis[v]=dis[x]+1;
				if(v==t) return 1;
			}
		}
	}
	return 0;
}
inline ll dfs(ll u,ll sum) { //sum代表流到这个点的时候还剩多少流量
	if (u==t) return sum;
	ll k,res=0;
	for (ll i=now[u];i&&sum;i=e[i].next) {
		now[u]=i;
		ll v=e[i].to;
		if (e[i].w>0&&(dis[v]==dis[u]+1)) {
			k=dfs(v,min(e[i].w,sum));
			if (k==0) dis[v]=inf;
			e[i].w-=k;
			e[i^1].w+=k;
			res+=k;
			sum-=k;
         //sum减去每一条边分走的流量，当sum为零的时候意味着无法继续做贡献，break掉就好。
		}
		
	}
	return res;
}
inline ll in() {
    char a=getchar();
	ll t=0,f=1;
	while(a<'0'||a>'9') {if (a=='-') f=-1;a=getchar();}
    while(a>='0'&&a<='9') {t=(t<<1)+(t<<3)+a-'0';a=getchar();}
    return t*f;
}
signed main() {
	n=in(),m=in();s=in(),t=in();
	for (ll i=1;i<=m;++i) {
		ll u=in(),v=in(),w=in();
		add(u,v,w);
	}
	while (bfs()) {
		ans+=dfs(s,inf);
	}
	printf("%lld",ans);
	return 0;
}

要点：

$now_i$ 为当前弧优化：我们每次 dfs 时都会把每条找到的增广路“榨干”，即下一次这条增广路不会再对答案产生贡献，所以下次再遍历的时候就直接从这条边开始遍历就可以了。
sum的用处在代码上标注。
与 KM 不同的就是在其基础上分层后再进行找增广路。分层的原因：优化时间复杂度
为什么要建反边：如果乱序遍历增广路，则可能找到的答案不是最大流，那么我们在遍历的时候，如果一次找到的增广路并不是我们真正要的那一条，若不建反边，则程序会不可逆的出现错误。而建了反边之后，如果这一次我们找错了增广路，下一次还要经过其中一条已经用过的边时，还可以无影响的找到我们需要的增广路。

通俗的话来讲就是：小流量不小心流到了大流量的管道里面，使得大流量管道在之后没法让大流量通过那么多了。我们当然不可能主动地让小流量往小管道里跑，但是我们可以这样做：假如我的小流量真的不小心流到你的大流量管道里面了，我可以做一个标记：虽然我占用了您的大流量管道，但是现在我的小流量管道是空着的，您但用无妨。

总体来讲：bfs 判断是否还有增广路+还原 $now$ 数组+分层；dfs 找这条增广路的贡献。

最小割：

定理：最大流 $=$ 最小割

视频证明与讲解

输出方案：

从 $s$ 跑 dfs 对其可到达的点（某条边可通过当且仅当其容量 $w$ 大于 $0$）染色为黑，否则为白，则若一个边两端点为一黑一白，则作为方案之一输出。

证明：

最小割跑完的残余网络已经使一些边不连通，这相当于有一些边已经被割掉了，所以这些边就是割边。

一个写得很好的博客

例题：Sabotage

最大流+最小割经典建模&做题笔记：

题单

拆点：

核心思想：将对点的限制转化为对边的限制

1. 建容量为一的边满足题目的【唯一性】限制，拆点建边满足容量限制。

例题：P2472 [SCOI2007] 蜥蜴

建图：

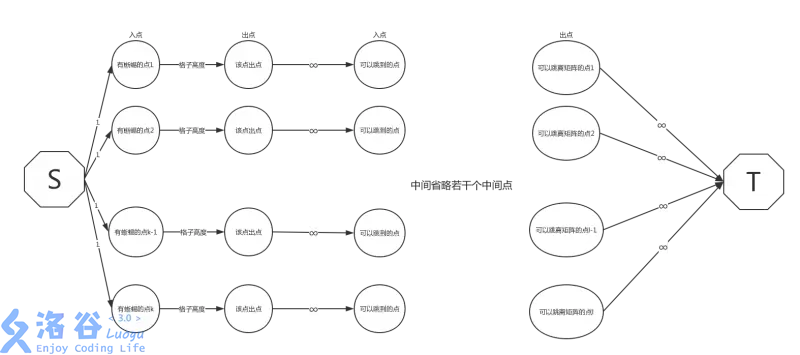
容量为一的边代表每个柱子上只能有一个蜥蜴。

容量为每个柱子上的使用次数的边表示对柱子使用次数的限制。

其他的边建无限大表示希望尽量多的蜥蜴逃生（不做对图的限制）

2.例题：P3254 圆桌问题

2. 拆点并建容量为一的边满足题目限制。

例题：P1402 酒店之王

建图：

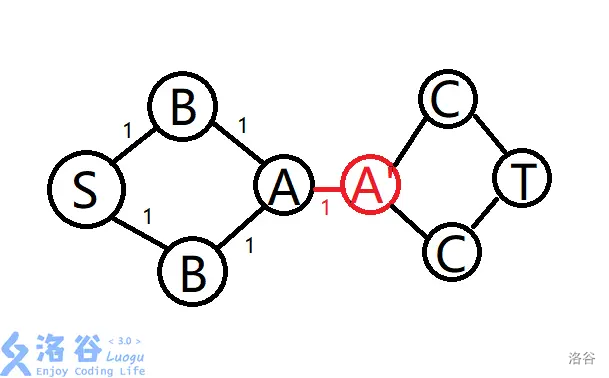
将所有的每个人喜欢的房间与每个人连边，再将每个人拆点，将每个人拆出来的第二个点与每一个他喜欢的菜连边。该图边权全部为一。

将人拆点代表每个人只选一种菜和一个房间。

为什么不按人—> 房—> 菜的顺序连边呢？

如果直接连的话体现不出来人与菜的直接对应关系，若拆点的话则会很麻烦。

3. 求最小割边数量转化为最小割割点数量时将每个点拆点连边。

例题：P1345 [USACO5.4]奶牛的电信Telecowmunication

题意简述：求一张无向带权图使其源点汇点不连通的最小割点数量。

建图：我们将每个点拆成两个并将他们两个中间连一条边权为一的边代表割点代价为一。

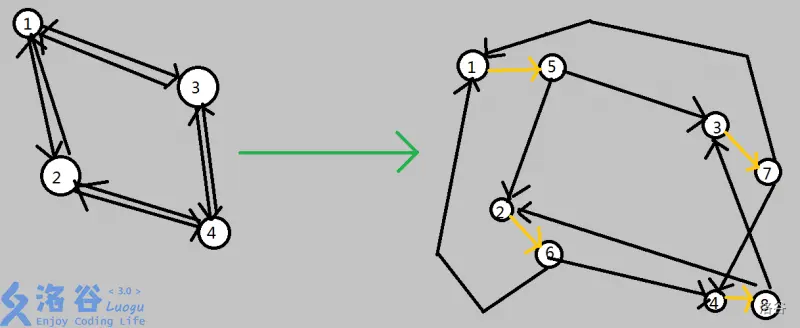
这样建图后最小割数量肯定会转化为割掉的点的数量，因为原图最小割一定大于等于割点数量（画图可自证），所以现图为了最小化代价，肯定要选择两点之间的边进行割边，所以割掉的边的数量一定是割掉的点的数量。

4. 求最小割时拆点建边以去重

例题：P3866 [TJOI2009] 战争游戏

分析题意，意思是不能让敌人通过格子之间的移动走出边界，而阻止敌军从一个格子到另一个子的途径是什么——花费敌军要到的格子所需的代价来建墙。

由此如果我们把每个格子之间都建一条边权为终点格子的建墙代价的边，再将源点连向每个敌人边权为无穷大，再把每个边界点向汇点连无穷大的边，最后求一下这张图的最小割不就是答案了吗？（以上建边均不包含起点或终点为障碍或终点为敌人的情况，原因显然。）

于是错误的解法诞生了，如下图所示：

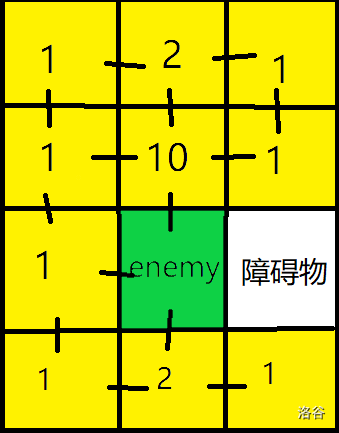
这个看似很对的解法虽然很接近正解了，但为什么是错的呢？

这样建图的话，如果有多个敌人的话，向敌人周围的格子建边可能会产生重复，比如三个敌人坐标分别为 $(i,j),(i+1,j-1),(i+1,j+1)$，此时我们想要在 $(i+1,j)$ 建墙的话，因为三个敌人都向这个坐标连过边，这样不就产生重复了吗。

于是，我们使用拆点法。

将每个坐标（障碍格除外），拆分成两个点，分别作为入点和出点，边权为这个坐标修墙的代价，再将出点向其他他相邻的非障碍且非敌人格的入点连边权为无穷大的边，最后将边界点的出点向汇点连边权为无穷大的边，将源点向敌人格的入点连边权为无穷大的边。

这样就解决了边权重复计算的问题。

最终答案就是这张图的最小割。

Question：

这样的建边每两个空格子之间会建两条边，不会导致边权计算重复吗？

首先，不这样建边的话显然是错误的，因为不能覆盖所有情况（比如我只能到一个格子而不能从一个格子出去）。其次这样建边只有每个格子拆出来的两个点之间才有非无限的的连边（最小割一定只会割这些边），并且是单向边，起点和终点只会有起点的出点向终点的入点连的边，即为边权值会计算一次，不会产生重复。

建无限大边权的边意义是什么？

因为我们要求最小割，就要保持图的联通，但是我们又不能因为这些为了保持图联通而不对答案产生贡献边影响答案，所以建无穷大的边，这样我们求最小割的时候才不会选上这些边。

（类）最大权闭合图

1. 最大权闭合图模板：

例题：P2762 太空飞行计划问题，P3410 拍照

简化题意：有 $m$ 个人，$n$ 种使用需要付费的仪器，花费分别为 $V_{n_i}$。这 $m$ 个人每个人做实验，完成后分别会得到 $w_{m_i}$ 的盈利，但会使用 $k_{m_i}$ 种仪器。一个仪器被多次使用时只需收费一次，请你安排一些人去做实验使的总获利最大。

像这种题意的题目，就是最大权闭合图模型。

建图：

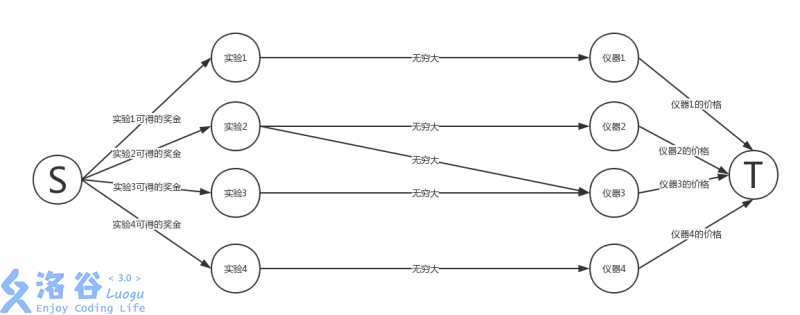
这样建图之后答案即为所有任务的盈利和 $-$ 新建图的最小割。

证明：

如果我们选择了 $p$ 个人让他们不做实验，那么则需要付剩下的 $m-p$ 个人所需的全部仪器的费用。转化到图上，即是构成了这张图的一个割，这个可以画图自证。那么此时的利润即为 $m-p$ 个人的利润 $-$ 这 $m-p$ 个人仪器费用 $=\sum w-p$ 个不工作的人的利润 $-$ 这 $(m-p)$ 个人仪器费用 $=\sum w-$ 这张图的割。

为了利润更大，则减去最小割即可。

证毕。

例题2：P2805 [NOI2009] 植物大战僵尸

拓扑+最大闭合权图

其实比较简单，不要想复杂，找对逻辑关系。

一种建图方法：将正边权的与源点相连，将负边权取绝对值与汇点相连。

例题3：P3749 [六省联考 2017] 寿司餐厅

最大权闭合图可以在有需要的情况下中间划分三部分，当前物品正收益，当前物品负收益，当前物品所属类收益。

例题4：P3153 [CQOI2009]跳舞

两种拆点方式：

first：

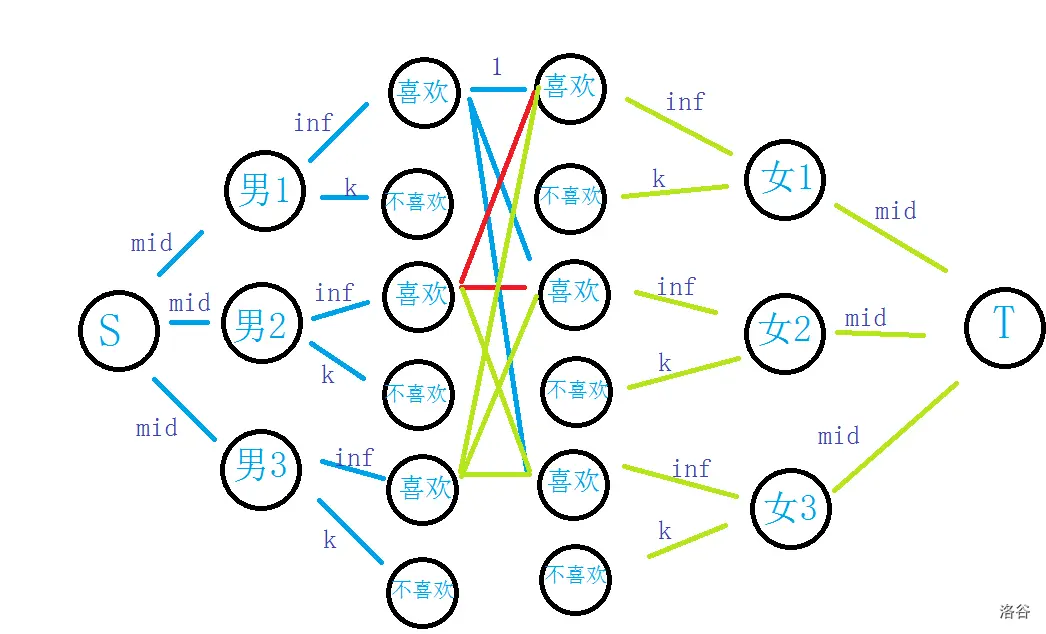
中间边权为1

second：

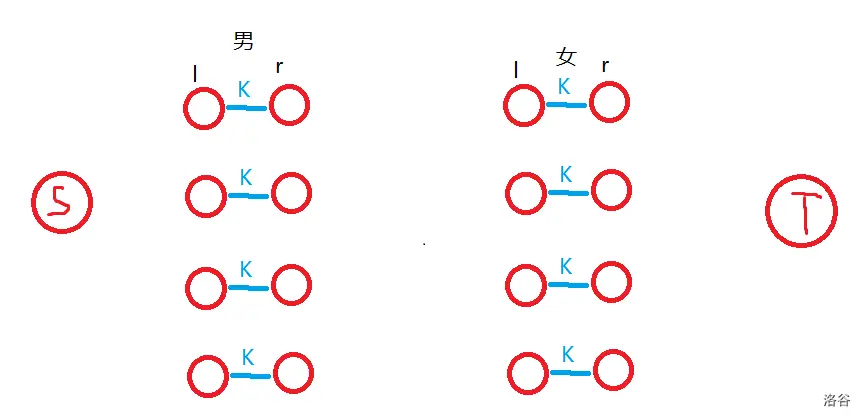
l —> r,r —> l

2.可花费代价不选某花费

例题1：P3872 [TJOI2010]电影迷

如果我们将正点权和负点权分类，将正点权连向负点权，再将源点和正点权联通，负点权和汇点联通，就是模板了，但是这里有一个条件：花一定价钱可以不选某个花费。

解决方案：将正点权与负点权连的边设为选了其一不选其二的代价，接下来正常做即可，原理和模板一样。

负点权能向正点权连边的原因和、可参照模板分析。

例题2： P4177 [CEOI2008] order

做法和刚才一样，可以多付几次租金去抵消一次购买。

组合权值模型：

此类题型的共同点首先是将每个物品连向 $s$ 代表一种选的情况及其费用/利益，连向 $t$ 代表另一种选的情况和费用/利益，利用最小割去解决费用最小问题。对于要求利益最大的话，就总权值$-$最小割（如例1）

例题1：P4313 文理分科

首先考虑一种简单情况：

S 代表选文科，T 代表选理科

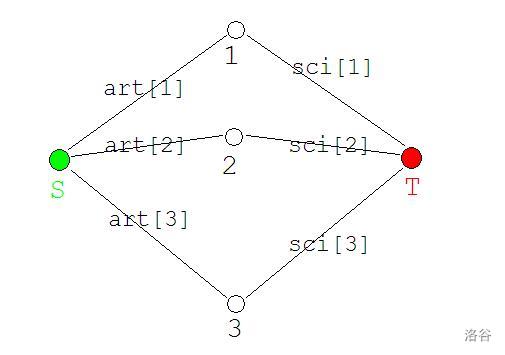
很显然，这张图的答案即为 权值和-最小割。

割掉的边即为不选。

接下来考虑情况：

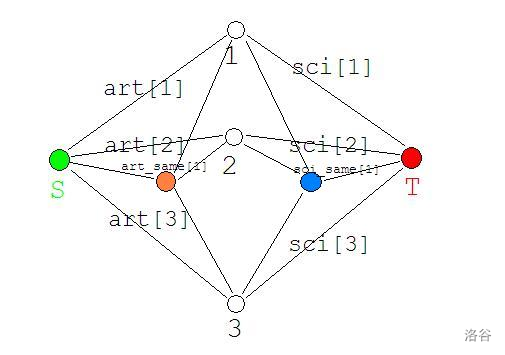
我们发现如果我们在保证最小割的前提下，割断了 $art_1$，那么为了图在此基础上不连通，则 $S$ 与橙点之间的边一定要被割掉，否则割掉 $art_1$ 就是无意义的。同理，如果我们割掉了 $S$ 与橙点之间的边，那么 $art_i$ 也一定要被割掉。

由此上面的图就是我们的建图方式，其中有标记的边边权即为标记，无标记的边中，$S$ 与橙点之间连的权值为橙点相连的点组合在一起产生的贡献。蓝点和 $T$ 同理。

一道此模型转化而来的好题：Biologist

所以由这道题的经验，以后再求最值的时候可以联想到割掉边即为不选的情况，以此建模。

例题2：P1935 [国家集训队]圈地计划

黑白染色思想+模板

黑白染色：

发现只有黑色点能影响白色，白色同理。

所以我们只需将黑点的 $A$ 和 $B$ 交换即可。

后面就是模板。

（类）组合权值模型

例题：水塘 Pool construction

一道真的很值得做的好题！！

题目让我们求费用最小值，于是我们可以尝试最小割，让割掉的作为费用。

观察到一个格子要么是水塘，要么是草地，所以如果我们想要将一个格子的属性变化的话，一定要把它在图中割掉。所以我们不妨将源点连向每一个格子，再将每一个格子连向汇点，源点连向格子代表把这个格子变成草地需要花费的费用，格子连向汇点代表这个格子变成水洼的费用。为了让图变的不连通，我们一定要割掉其中一个，这就代表着花费/不花费钱去改变/不改变该格子属性。

接下来就是将赋容量了。

根据我们刚才连边的意义，如果这个格子原本是草地，那么源点向他的连边为 $0$，意味着它本来就是草地，（变成草地）不需要花费任何费用；连向汇点的边容量就要为 $d$，代表花费 $d$ 去将他变为水洼。如果这个格子是水洼同理，源点向其连边容量 $f$，它向汇点连边容量 $0$。

但这还没完，还需要建围栏。

于是我们将每一个格子向其相邻格子连一个容量 $b$ 的边，如果两个格子属性不同，只有割掉这条边才能使图不连通，否则不需要割。

双人关联模型：

例题：[SHOI2007] 善意的投票 / [JLOI2010] 冠军调查

建图方式：

将源点连向不睡觉的，将睡觉的连向汇点，然后将每队朋友之间建双向边，所有建的边边权都为一。

考虑为什么是对的？

当一个人改变自己意见的同时不没有人原本和自己意愿相同，显然成立。

如果不满足上述情况，那么这就体现出建双向边的含义了，建双向边能在一个人改变自己意愿又违背了原本和自己意愿相同的人的时候，原本和自己意愿相同的人仍能通过边来找到刚刚这个人，意味着还需再割一条边。

与二分图结合：

例题：P2774 方格取数问题

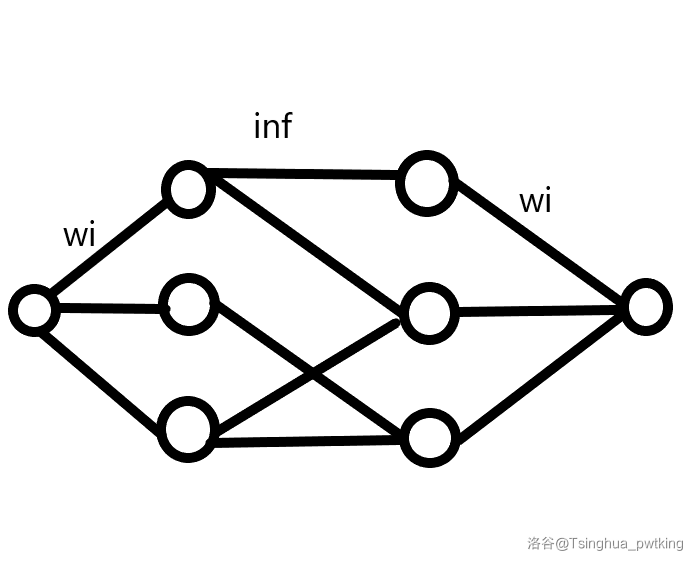
法一：将图黑白染色，发现只有不同颜色的格子才会互相约束，所以将黑点向其相邻白点连边权 inf 边，将源点与黑点连黑点边权边，将白点与汇点连白点边权边。
答案即为 $\sum w-$ 最小割。
法二：不进行染色，直接像刚才一样对每个点向其相邻点进行连边，但这样会产生重复，所以答案为 $\sum w- \frac {1}{2}$ 最小割。

建图如图所示：

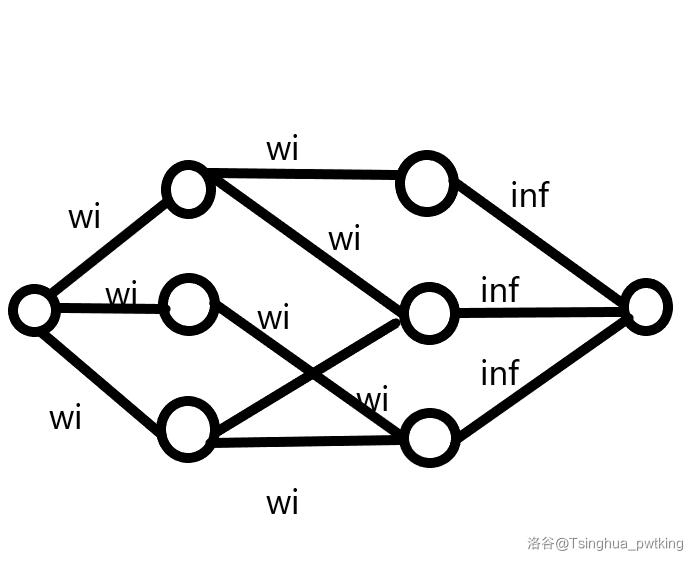
警钟敲烂：

这种建图是毫无意义的，最小割/最大流永远只会为左边的 $\sum w_i$。

原因可手模

与二分结合

通常会二分一个建边的门槛来跑最大流观察是否符合答案要求

P2402 奶牛隐藏

二分阈值，用阈值建边达成限制

P3425 [POI2005]KOS-Dicing

看到"最大值最小",显然要二分最少赢多少场。

源点向每一个比赛连一条流量为1的边，表明每个比赛只能赢一次

每个比赛向2位选手各连一条流量为1的边，表明每个比赛只能有一个人赢

最后每个选手向汇点连一条流量为mid的边，如果总流量>=比赛数，那么这个做
法可行

等等，要输出方案！

每一个比赛向哪一个选手连的边流量是1，就代表这个选手赢了

多源多汇问题

P3163 [CQOI2014]危桥

题目中提及到有两个源点和两个汇点，我们可以建一个超级源点 $s$ 和一个超级汇点 $t$。

将 $s$ 连向 $a_1,b_1$，将 $a_2,b_2$ 连向 $t$，边权分别都为 $a_n,b_n$。

其他的点与点之间的连边为两点之间可通过次数。

可是这样是错误的：

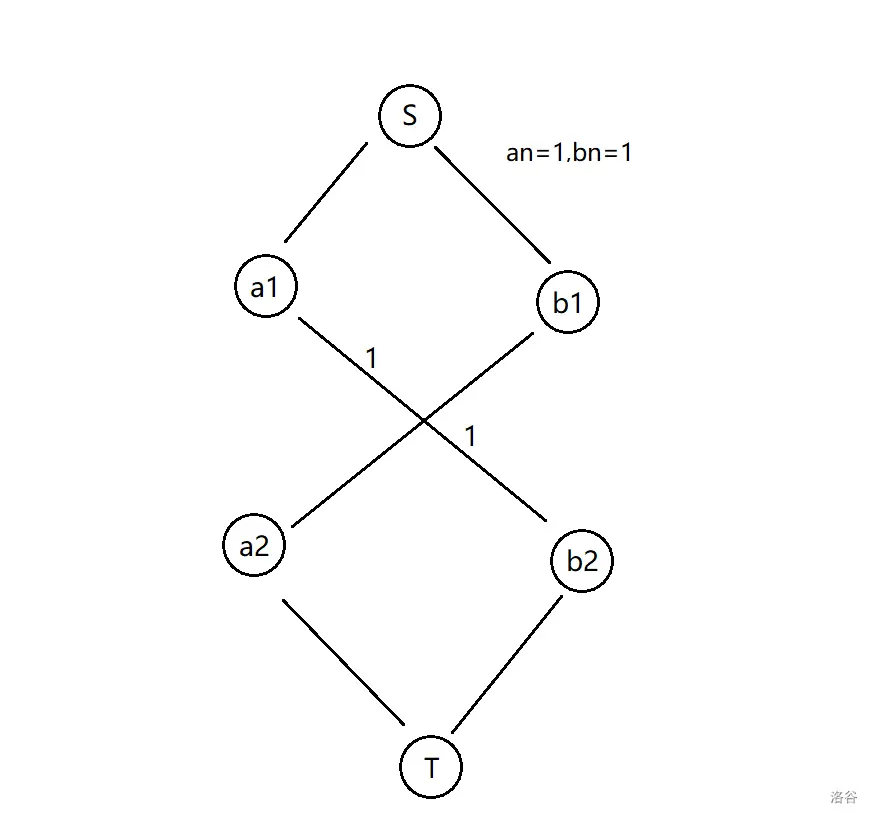
因为可能从 $a_1$ 起始的流量流到了 $b_2$。

所以将 $b_1,b_2$ 的位置调换一下，其他连变不变再跑一次最大流，如果也满足要求，输出 $yes$。

网格图黑白染色：

通常使用条件：

某次操作会使自身坐标相邻的产生权值变化。

不定源汇点问题

电视网络 Cable TV Network

想出如何连边很容易：将每个点拆点，输入的每条边的 $(u,v)$ 正常从出点连向入点连上双向边，最后跑最小割即可。

问题是这道题无法确定源汇点！

如果建立虚拟源汇点的话，那么为保持图联通必须要把源点向所有入点都连边，把所有出点向汇点连边，但这样最小割的答案就改变了；而我们又无法在图中找到合适的源汇点保证答案最小。

这时我们可以枚举源汇点，把所有的点作为源汇点的情况全部跑一边取最小值即可

费用流

主要思想：将dinic/KM的 bfs 部分换成 spfa。

为什么 dfs 部分需要 $vis$ 数组？

原 dinic 算法 bfs 将图进行分层，而 spfa 无法进行分层，所以需 $vis$ 判重。

目前最优模板（zwk费用流）：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inf 0x7fffffff
const ll maxn=100010;
ll n,m,s,t;
ll head[maxn],dis[maxn],vis[maxn];
ll inq[maxn];
struct edge {ll to,next,w,cost;}e[maxn];
ll cnte=1,cur[maxn];
ll Cost,ans;
inline void add(ll u,ll v,ll w,ll c) {
	e[++cnte].to=v,e[cnte].w=w,e[cnte].cost=c,e[cnte].next=head[u],head[u]=cnte;
	e[++cnte].to=u,e[cnte].w=0,e[cnte].cost=-c,e[cnte].next=head[v],head[v]=cnte;
}
inline bool spfa() {
	queue<ll> q;
	for (ll i=0;i<=n;++i) dis[i]=inf,cur[i]=head[i];
	q.push(s);
	dis[s]=0,inq[s]=1;
	while (!q.empty()) {
		ll u=q.front();
		q.pop();
		inq[u]=0;//加inq作用：优化运行效率
		for (ll i=head[u];i;i=e[i].next) {
			ll v=e[i].to;
			if (e[i].w>0&&dis[v]>dis[u]+e[i].cost) {
				dis[v]=dis[u]+e[i].cost;
				if (!inq[v]) q.push(v),inq[v]=1;
			}
		}
	}
	return (dis[t]!=inf);
}
inline ll dfs(ll u,ll sum) {
	vis[u]=1;
	if (u==t) return sum;
	ll tmp=0,used=0;
	for (ll i=cur[u];i;i=e[i].next) {
		cur[u]=i;
		ll v=e[i].to;
		if (e[i].w>0&&dis[v]==dis[u]+e[i].cost&&(!vis[v]||v==t)&&(tmp=dfs(v,min(e[i].w,sum-used)))) {
			e[i].w-=tmp,e[i^1].w+=tmp;
			Cost+=e[i].cost*tmp;
			used+=tmp;
			if (used>=sum) break;
		}
	}
	vis[u]=0;//小优化，加上之后快20ms
	return used;
}
inline void dinic() {
	ans=Cost=0;
	while (spfa()) ans+=dfs(s,inf);

//此处在不影响正确性情况下优化运行效率
}
inline ll in() {
    char a=getchar();
	ll t=0,f=1;
	while(a<'0'||a>'9') {if (a=='-') f=-1;a=getchar();}
    while(a>='0'&&a<='9') {t=(t<<1)+(t<<3)+a-'0';a=getchar();}
    return t*f;
}
signed main() {
	n=in(),m=in(),s=in(),t=in();
	for (ll i=1;i<=m;++i) {
		ll u=in(),v=in(),w=in(),c=in();
		add(u,v,w,c);
	}
	dinic();
	printf("%lld %lld",ans,Cost);
	return 0;
}

注意！注意！注意！

while (spfa()) ans+=dfs(s,inf);

这一句只能在求单张图费用流使用，多张图的话需要在每次跑的时候加

memset(vis,0,sizeof(vis));

或者在 dinic 函数部分改为：

while (spfa()) {
        ans+=dfs(s,inf);
        memset(vis,0,sizeof(vis));
		while (vis[t]);{
			memset(vis,0,sizeof(vis));
			ans+=dfs(s,inf);
		}
	}

警钟敲烂：因为spfa不能跑负环，所以这个算法不能跑带负环的图。

系列trick（不含最大流部分已包含的）：

主要题单

更巧妙の拆点

1. 最小路径覆盖：

P2469 [SDOI2010]星际竞速

设源点 $s$ 意味起点，汇点 $t$ 作为任务结束点。

将每个星球拆点为 $u,u+n$，分别代表每个点作为任务起始点和任务终止点。将源点向 $u+n$ 连 $a_i$ 代价，容量为 $1$ 代表瞬移到 $u$，再将 $s$ 连向 $u$ 费用 $0$ 容量 $1$ 表示任选一个星球作为起点，将每条路径 $E(u,v,w)$ 连边 $u \to v$ 费用 $w$，容量 $1$ 代表航线，最后将所有 $u_i \to t$ 费用 $0$ 流量 $1$。

2. 拆点满足单点多个任务需求：

P1251 餐巾计划问题

每一天既要使用毛巾又要产生脏毛巾并进行清洗或重购，于是我们可以将一天拆为早上（$day_i$）和晚上（$day_i+n$）两个点，代表早上需要新毛巾，晚上产生脏毛巾。

送到快洗部属于结束点操作，连向i+m天后的起始点，费用为f（表示餐巾洗好了，可使用）
送到慢洗部属于结束点操作，连向i+n天后的起始点，费用为s
延期送洗属于结束点操作，连向i+1的结束点，不需费用。

解释一下这一步：因为如果没有上述操作那么根据前两个操作，当天产生的毛巾必须在 $i+n$ 或 $i+m$ 天后使用，致使不能延期使用，所以此操作可实现毛巾储存；而新买的毛巾即买即用即可，没必要储存。

购买新的餐巾的操作也应是连向每天起始点的边，目前并没有确定从哪连的，但费用为p。

以上操作流量均为 inf.

接下来要将汇点向 $day_i$ 连边，源点向 $day_i+n$ 连边。

为什么这样练呢？很不符合人的直觉啊。

将源点/汇点向每个点联通的主要作用之一还有：将图能将流量从源点流向汇点。而本题刚刚提到的连边大多数为从 $day_i+n$ 连向 $day_i$。所以为了图的连通性，应这样连。

3.拆点满足多个状态

P2053 [SCOI2007] 修车

最大的难点为每个人等待时间受前面人的影响。

于是我们将每个工人拆成 $n$ 个点，分别将每个车连向每层的每个工人，代表这个车倒数第 $k,k \in[1,n]$ 个人来修所需时间。于是费用为倒数第 $k$ 人修所等待的时间。最后将源点向每个车连边，每层工人向汇点连边保持图联通即可。

4. 与二分图匹配思想，黑白染色思想结合的高级双重拆点

P4142 洞穴遇险

主要思想：拆点，黑白染色。

首先能想到的是只在 $x+y$ 为奇数的格子上放柱子，原因显然。

接下来转化题意：求最小不稳定数不就是求放柱子能减少的最大不稳定数，于是我们现在着力解决放柱子能减少的最大不稳定数。

题目已经暗示我们要黑白染色，于是网格点被染为两类： $x+y$ 为奇数（我们称为黑点）和 $x+y$ 为偶数（我们称为白点）。

于是想到一个错误但能为正解提供思路的想法：

我们考虑类似二分图匹配的方式：因为每个偶数格子只能被选一次，所以将源点向每个黑点连边。在将每个能放柱子的黑点向每个与他相邻白点连边，再将每个白点向汇点连边。但是因为每个黑点上的柱子只会占用他相邻的两个柱子，所以将黑点拆点作为入点和出点，将黑点的入点与出点之间连容量为 $2$ 的边代表每个黑点只会占用他相邻的两个白点。

这个做法看似很对，但是有个很显然的问题：无法保证它占用的连个白点位置是否满足形状要求，于是这个做法陷入僵局了。

但我们只需要在此基础上满足最后图形形状限制就好了，怎么做呢？

既然我们将黑点拆点满足了黑点只能占两个白点的限制，那我们考虑用类似的方法也满足白点限制就行了。但显然拆点是无能为力了，观察到每个黑点只会占用相邻的两个处于不同奇偶性列数的白点，于是我们试试黑白染色：我们再将处于奇数列白点染为灰色，否则仍为白点。

这时我们可以将灰点连向黑点，再将黑点连向白点，容量为 $1$。只不过此时我们黑点入点与出点之间的边容量需要改为 $1$；将源点向汇点连边，将白点向汇点连边。

总结：

将源点向每个灰点连费用 $0$ 容量 $1$ 的边代表每个灰点只能选一次。
将灰点向他每个相邻的黑点的入点连费用 $0$ 容量 $1$ 的边代表每个灰点只能匹配一个黑点。
将黑点的入点和出点之间连费用 $w_{x,y}$ 容量 $1$ 的边代表每个黑点只能选一次且费用为该点权值（$(x,y)$ 为该点坐标）。
将黑点出点向他每个相邻的白点连费用 $0$ 容量 $1$ 的边代表每个黑点只会占用一个白点。
最后将白点向汇点连费用 $0$ 容量 $1$ 的边代表每个白点只选一次。

以上连边均不包含已经坍塌的点。

拆边：

1.拆边满足多种任务需求

例题：P2045 方格取数加强版

拆点的套路很 trick，不再赘述，但是在拆点的过程中我们发现虽然一个格子里的数只为答案贡献一次，但他可以无限次走，如果单点拆除的两个点之间只连容量 $1$ 费用 $w_i$ 的边则无法实现多次经过该点。

于是我们再建一条容量 $inf$ 费用 $0$ 的边代表这个点可以无数次经过。

2. 两点之间的连边费用每次不同时

P4307 [JSOI2009] 球队收益 / 球队预算

观察到每次每个队伍赢了之后多付出的费用不同，于是拆边，拆成 每个队伍最多能赢几次 条边，每条边费用为每次增加的费用，容量为一。

接下来源点连每场比赛，费用 $0$ 容量 $1$，代表每个比赛只能比一次且只能赢一次。再将每个比赛分别向 $2$ 个比赛球队连边，费用 $0$ 容量 $1$，代表每场球队只能有一个赢。

Transportation

拆边裸题，和上题做法一样，每条边建不同费用

打破常规の跳点（一流对多流）

这类问题就是解决用单流解决区间覆盖的问题

例一：P3980 [NOI2008] 志愿者招募

这道题最大的难点就是如何连边才达到区间覆盖的效果。

于是我们不妨将源点向 $1$ 连费用 $0$ 容量 inf 的边，$n+1$ 向汇点连通费用 $0$ 容量 inf 的边保证图的联通。然后将每一天连一条边代表每一天的人数需求。

但我们发现天数之间的连边容量如果设置成 $a_i$ 的话会导致某一天限流，于是我们可以将容量设置为 $inf-a_i$，这样不会被限流，而且代表某天到某天的要求人数减少或增多，满足需求。

对于一次花费必须连续让他工作，所以我们可以将工作起始日向终止日连边代表 这个人为满足第 $v$ 天的工作贡献流量 。费用为这个人的费用，容量 inf。

如下图所示：

。

例2：P3358 最长k可重区间集问题

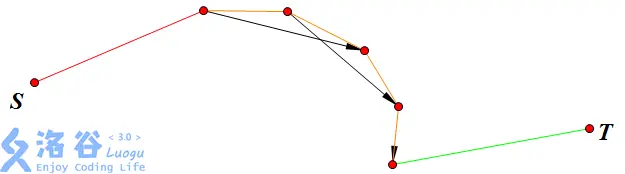经典的一流对多流的问题。

问题实质上的限制就是不能有不能有超过 $k$ 个线段重合，于是为了实现线段能“区间覆盖”，采用一流对多流。

将线段离散化，将每个横坐标之间连一个费用 $0$ 容量 $k$ 表示限流，再将每条线段的 $l \to r$，费用 $-len_{l,r}$，容量 $1$。

例3：P3357 最长k可重线段集问题

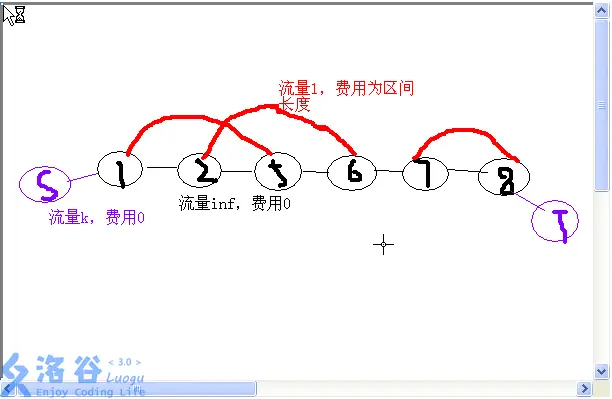
与例 2 不同的是这回将坐标改成坐标系了，但是一样的道理，将其转换在 $x$ 轴上即可

与二分图结合：

二分图带权最大匹配模板
P3440 [POI2006]SZK-Schools（其实也是模板）

建图方式的优化：

April Fools' Problem (medium)

首先有一种很显然的连边方式：

将 $a_i$ 和 $b_i$ 分开排列，将源点连向所有 $a_i$，容量 $1$ 代表每个 $a_i$ 只能选一次，费用 $a_i$，将每个 $a_i$ 连向每一个 $b_j,j\ge i$，容量 $1$，费用 $0$。再将每个 $b_j$ 连向汇点。

但是显然这样不能满足只选 $k$ 个数，所以我们将汇点拆点为 $t_0$ 和 $t$，将所有的 $b_j$ 连向 $t_0$，再将 $t_0$ 连向 $t$，费用 $0$ 容量 $k$ 以满足选数的个数限制。

但是此时复杂度又超了！

仔细观察发现其实我们将 $a_i$ 连向每个 $b_j$ 的实质是让源点向 $a_i$ 连的边与 $b_j$ 连的边连通以达到选每个数的目的，但其实完全没必要，我们可以把所有的 $a$ 和 $b$ 缩成一个点 $i$。将源点向每个 $i$ 连边，费用 $a_i$ 容量 $1$，将每个 $i$ 向 $t_0$ 连费用 $b_i$ 容量 $1$ 的边，最后将每一个 $i\in[1,n)$ 向 $i+1$ 连费用 $0$ 容量 $1$ 的边代表我可以选所有比当前 $i$ 更大的 $i+x$。

无固定源汇点问题：

和最大流时候其实思路都通用。

例题

题意简述：

给定一个 $n$ 点 $m$ 条边的有向无环图，你需要求出两组点 $(u_1,v_1)$，$(u_2,v_2)$ 使得 $u_1$ 到 $v_1$ 的路径与 $u_2$ 到 $v_2$ 的路径不相交且这两条路径长度和（经过的点数和）最大。注意：两条路径的起点和终点也不能重合。

输入：

第一行一个 $T$，代表数据组数。

接下来每一组数据第一行为 $n,m$，接下来的 $m$ 行每一行两个数 $u,v$ 代表一条有向边。

输出：

对于每组数据输出一个整数代表这两条路径的最大和。

显然是个网络流题，考虑使用费用流。

观察到本题没有给定源汇点，然而如果我们挨个枚举的话显然直接 T 飞。

我们考虑新建一个虚拟源点 $s'$，一个总源点 $s$ 和一个汇点 $t$。将 $s'$ 向每个点连容量 $1$ 费用 $0$ 的边代表每个点（入点，后面会说到）作为起点只能使用一次，再将 $s$ 连向 $s'$ 容量为 $2$ 费用 $0$ 代表需要两个起点。
因为这里已经限过流了，所以 $t$ 无需再限流。

无固定源汇点的问题解决了，接下来解决路径不相交问题。

将每个点拆点为入点和出点，入点和出点之间连容量 $1$ 费用 $-1$，这样限制了每个点的经过次数只有一次，因为是最小费用流，所以费用设为 $-1$，最后结果取相反数就行了。输入的边将出点连向入点即可，费用 $0$ 容量 $1$ 限制每条边只能走一次。

最后将每个出点连向 $t$，费用 $0$ 容量 $1$ 代表每个点作为终点也只能使用一次。

上下界网络流

这个东西确实非！常！难！理！解！。

~~这才是正儿八经的【省选/noi-】吧~~

笔记链接||题单

有源汇上下界最大流：

模板题：P5192 Zoj3229 Shoot the Bullet|东方文花帖|【模板】有源汇上下界最大流

对思路的理解：

声明：我们以下所说的【新图】指的是我们在原图的基础上为满足流量平衡加边形成的图，而【旧图】指的是未进行加边的原图。【旧图】是【新图】的子图。

首先：

真实上界$-$真实的流量$=$ 虚拟上界（新建图的容量（即原上界-原下界））$-$虚拟流量（在新图中跑出来的）

是显然成立的。

所以原图其实和新图在意义上是等价的，只是新图我们强制让它满足了下界。

所以可以认为新图跑出的答案是【可行额外流】

而此时 $t\to s$ 的连边正好帮我们再平衡流量的同时，又加上了下界，所以真正的最终可行流结果是 $t\to s$ 反边上的流量。

但是我们要求的是【最大流】。

最后再将 $t\to s$ 删去（只删他及他的反边即可）。

Q&A：

为什么要将 $t \to s$？

根据网络流的概念，除了源点及汇点以外，其他的点流量应平衡，即：出流量=入流量。源点应满足只有出流量没有入流量，汇点应满足只有入流量没有出流量。而我们为平衡流量建了一个新的源汇点，所以我们现在也应该将原源汇点当作普通点处理，所以 $t\to s$ 满足其流量平衡。

为什么要在跑完一次之后再进行跑一次？

很显然，我们看似在新图跑的是【最大流】，但实际上是为了其在满足下界+满足流量平衡的情况下的一种可行流（因为我们新建了一车边，并且源汇点也是新建的）。所以我们跑出的【最大流】并不是我们以为的【最大流】，而是一种可行流，而可行流不一定最大。

跑完一次之后为什么要在【跑完的新图的基础上】再【在旧图上】跑一次？

这张图已经满足了流量平衡，而你现在如果在新建一张图，显然不一定仍满足条件。

有源汇上下界最小流：

模板：P4843 清理雪道

思想其实和最大流一样，只是一个是【可行流+可浮动流】，另一个是【可行流-可浮动流】。

警告⚠⚠⚠：

跑最小流的时候：

一定不要用费用流模板来跑！！！！

（跑最大流的时候可以用费用流模板）

会出现玄学死循环

原因玄学。

最小流方法其二：

除了在【上下界网络流】标题上放的学习笔记上写的一种意外还有一种：

首先 $t\to s$，跑一次最大流。
删去 $t\to s$ 这条边（全删，包括 $e[cnt].next,e[cnt].w,e[cnt].to$ 及其反边），将当前源点设为【原汇点】，当前汇点设为【原源点】（这个注意不要搞混）。
再跑一次最大流，答案就是【第一次跑出的 $e[cnt].w-$ 第二次跑出的 $ans$】。

第二条的原理：跑最大流的时候不对调，实现我【能上浮多少】，我们将原源汇点对调，这样实现【能下浮多少】，即我能正着来，我就能反着回去。

有源汇上下界费用流

这里通常指的是【有源汇上下界可行流最小费用流】。

模板：P4043 [AHOI2014/JSOI2014]支线剧情

这个东西其实跟我们的【有源汇最大流/可行流】的流程一样，只是多了一个费用。

唯一的区别就是答案为：跑出的费用 $+$ 所有边下界 $\times $ 该边费用。

为什么要加【所有边下界 $\times $ 该边费用】？

我们跑出的费用只是一个满足上下界的【额外费用】，因为我们新加的边没有费用。所以要再加上原有下界费用，来满足我的答案是建立在满足下界基础之上的。

那为什么跑最大流的时候不用加呢？

根据跑最大流的原理，我跑出的流量都会在他的反边上体现，但费用不会，所以我们就只能用跑出的费用值进行计算，而我们跑出的费用值时额外费用值，所以需要再加上下界。

为什么不常/没有听说过【有源汇上下界最大流最小费用流】或者【有源汇上下界最小流最小费用流】呢？

根据跑最大流/最小流的经验，我们应当二次跑费用流，但是此时残余网络上可能会出现【负费用环】，而导致死循环，所以就要有一个新的网络流方式【模板】有负圈的费用流来消除负环影响，但这样将会非常麻烦，所以一般不会这样出题。

上下界网络流经典trick：

什么，trick？

还想要 trick？

这玩意先理解透了会打板子吧，毕竟这玩意确实太难。

trick的话，先占坑，后期【可能】会补

终于，终于可以end了（两个多星期啊）

posted @ 2023-06-06 18:30 Pwtking 阅读(154) 评论(1) 收藏举报

刷新页面返回顶部

NOI2024游记

Pwtkingのblogs

【网 络 流（瘤）】——用普及的代码诠释着的noi级的难度

最大流：

要点：

最小割：

最大流+最小割经典建模&做题笔记：

拆点：

核心思想：将对点的限制转化为对边的限制

1. 建容量为一的边满足题目的【唯一性】限制，拆点建边满足容量限制。

2. 拆点并建容量为一的边满足题目限制。

3. 求最小割边数量转化为最小割割点数量时将每个点拆点连边。

4. 求最小割时拆点建边以去重

Question：

（类）最大权闭合图

1. 最大权闭合图模板：

2.可花费代价不选某花费

组合权值模型：

（类）组合权值模型

双人关联模型：

与二分图结合：

警钟敲烂：

与二分结合

多源多汇问题

网格图黑白染色：

不定源汇点问题

费用流

系列trick（不含最大流部分已包含的）：

更巧妙の拆点

1. 最小路径覆盖：

2. 拆点满足单点多个任务需求：

3.拆点满足多个状态

4. 与二分图匹配思想，黑白染色思想结合的高级双重拆点

拆边：

1.拆边满足多种任务需求

2. 两点之间的连边费用每次不同时

打破常规の跳点（一流对多流）

与二分图结合：

建图方式的优化：

无固定源汇点问题：

上下界网络流

有源汇上下界最大流：

有源汇上下界最小流：

警告⚠⚠⚠：

一定不要用费用流模板来跑！！！！

一定不要用费用流模板来跑！！！！

一定不要用费用流模板来跑！！！！

最小流方法其二：

有源汇上下界费用流

上下界网络流经典trick：

end

公告

【网络流（瘤）】——用普及的代码诠释着的noi级的难度