LG - P3573

给定一个 \(n\) 个点，\(m\) 条边的有向无环图，每条边长度都是 \(1\)。

请找到一个点，使得删掉的这个点之后剩余的图中的最长路径最短。

首先考虑暴力，可以枚举删掉哪一个点，之后再在拓扑排序上 DP，然后取一个 \(\max\) 即可，时间复杂度\(O(n(n+m))\)。

显然，这样太不优秀了，发现每次删除点的时候有很多地方是重复的，考虑通过重复部分简化。

首先，考虑已经被处理过的点的集合为 \(A\)，剩余点为 \(B\)。

考虑这样一个东西的最长路径，以下记 \(dped_a\) 表示以 \(a\) 节点为终点的最长路径的长度，\(dpst_a\) 表示以 \(a\) 节点为起点的最长路径的长度。

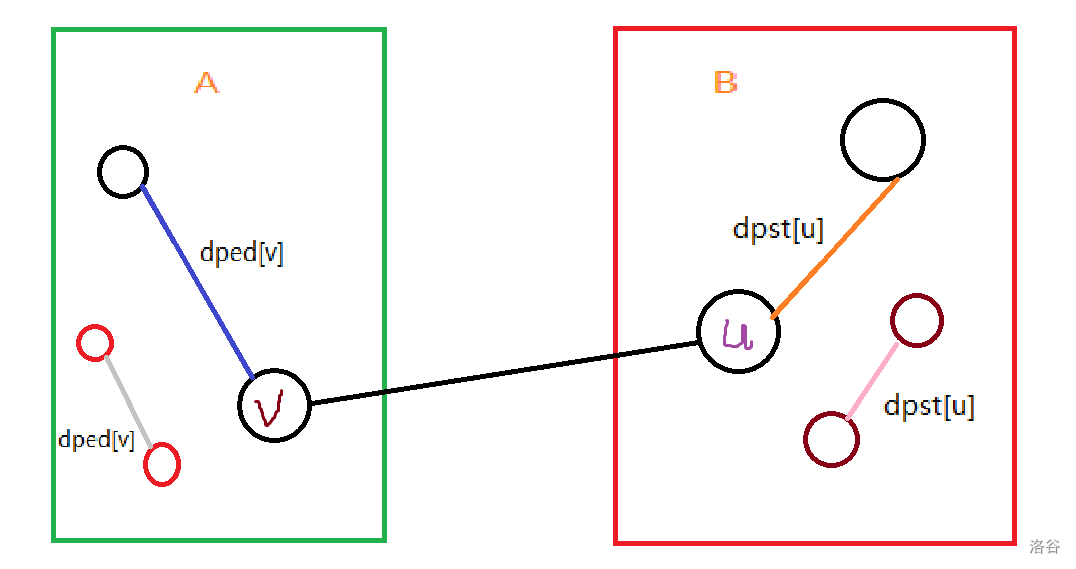
根据这个图片，可以得出，整个图的最长路径应该在 \(dped_v(v\ 在A中)\)，\(dpst_u(u\ 在B中)\)，\(dped_v+1+dpst_u(v\ 在A中,u\ 在B中,且\ v,u\ 有边)\)。

那么就需要将所有的边都算上，否则答案并不完全，第 \(3\) 类仅仅被计算了一部分。

考虑什么时候边不会被算上。对于一条 \(v\rightarrow u\) 的边，当且仅当 \(u\) 比 \(v\) 先进入集合 \(A\) 中，才不会算上这条边。

因此，要求就是对于每一条边 \(u\rightarrow v\)，\(u\) 都要比 \(v\) 提前进如集合 \(A\)。

这不就是拓扑排序的基本要求嘛，正好在求解 \(dped,dpst\) 的过程中，搞一个拓扑序就可以了。

那这样的话，只需要考虑一个点如何从 \(B\) 转化到 \(A\) 了，可以分成 \(3\) 步，首先，将这点从 \(B\) 中拿出来，然后处理删除这个点的结果，最后将这个点加入 \(A\)。

考虑如何将这个点从 \(B\) 中拿出来，对于整体来讲，减少了 \(2,3\) 部分的，直接删掉即可。

然后处理结果，直接取 \(1,2,3\) 三种结果的最大值结果。

考虑如何将这个点加入 \(A\)，增加了 \(1,3\) 部分的，直接加入即可。

于是，我们需要一个支持 单点加入/删除，求全局最大值 的数据结构，可以使用一个带修堆来维护。

\(code：\)

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+1000;


#define L(i,j,k) for(int i=j;i<=k;i++)
int n,m;

queue<int> Queue;

vector<int> edge[N],backedge[N];

int in[N],backin[N];

vector<int> tp;

int dpst[N];//以 i 为起点的最长路径
int dped[N];//以 i 为终点的最长路径

struct QUEUE{
	priority_queue<int> Q1,Q2;
	void push(int x){Q1.push(x);}
	void pop(int x){Q2.push(x);}
	int top(){while(!Q2.empty()&&Q1.top()==Q2.top()){Q1.pop();Q2.pop();}return Q1.top();}
}Q;

int main(){
	
#ifndef ONLINE_JUDGE
	freopen("in.in","r",stdin);
#endif
	
//	ios::sync_with_stdio(0);
	
	cin>>n>>m;
	
	
	
	L(i,1,m){
		int u,v;
		cin>>u>>v;
		edge[u].push_back(v);
		backedge[v].push_back(u);
		in[v]++;backin[u]++;
	}
	
	
	L(i,1,n)if(!in[i])tp.push_back(i),Queue.push(i);
	
	while(!Queue.empty()){
		int u=Queue.front();
		Queue.pop();
		for(int v: edge[u]){
			if(!(--in[v])){
				dpst[v]=max(dpst[v],dpst[u]+1);
				tp.push_back(v);
				Queue.push(v);
			}
		}
	}
	
	
	L(i,1,n)if(!backin[i])Queue.push(i);
	
	while(!Queue.empty()){
		int u=Queue.front();
		Queue.pop();
		for(int v: backedge[u]){
			if(!(--backin[v])){
				dped[v]=max(dped[u]+1,dped[v]);
				Queue.push(v);
			}
		}
	}
	
	
	
	L(i,1,n)Q.push(dped[i]);
	int ans=Q.top(),anspoint=0;
	
	for(int u: tp){
		Q.pop(dped[u]);
		for(int v: backedge[u])Q.pop(dpst[v]+dped[u]+1);
		int Max=Q.top();
		if(Max<=ans){
//			cout<<Max<<' '<<ans<<'\n';
			ans=Max;
			anspoint=u;
		}
		for(int v: edge[u])Q.push(dpst[u]+dped[v]+1);
		Q.push(dpst[u]);
	}
	cout<<anspoint<<' '<<ans<<'\n';
	return 0;
}