Date 2025.10.6
在 Print 之前
这场比赛打的不好,T1 没判边界挂了 \(50 pts\),T2、T3 都只打了 \(60 pts\),总的来说不算太好。
A - 玩具

P.S. \(n \le 100000 \quad t \le 100000 \quad w_{i} \le 100 \quad k_{i} \le 100\)
说真的这题我做了 \(90 min\),原本以为很简单(事实上也是)但还是想了很久。
不难发现,只需要在每次处理前缀和的余数时记录一下位置,便可以二分解决。
时间复杂度:\(O(n \times k \times logn)\)。
Code
#include <bits/stdc++.h>
#define pll pair<ll,ll>
#define pld pair<ld,ld>
typedef long long ll;
typedef long double ld;
typedef int praise_long_long;
namespace io {
using namespace std;
inline ll read() {
char x=getchar();
ll ans=0,f=1;
while(x<'0'||x>'9') {
if(x=='-') {
f*=(-1);
}
x=getchar();
}
while(x>='0'&&x<='9') {
ans*=10;
ans+=(x-'0');
x=getchar();
}
return ans*f;
}
inline void print(ll x) {
if(x<0) {
putchar('-');
x=-x;
}
if(x>=10) {
print(x/10);
putchar(x%10+'0');
}
else {
putchar(x+'0');
}
}
}
using namespace io;
const ll N=1e5+5,mod=1e9+7,inf=2e18;
const ld eps=1e-6;
struct node {
ll l,r,kl,wl;
} b[N];
ll n,m,a[N],s,sum[N];
bool vis[105];
vector<ll> num,f[105][105];
inline void solve() {
m=read(),n=read();
for(ll i=1;i<=n;i++) {
a[i]=read();
sum[i]=sum[i-1]+a[i];
}
for(ll i=1;i<=m;i++) {
b[i]={read(),read(),read(),read()};
if(!vis[b[i].kl]) {
num.push_back(b[i].kl);
}
vis[b[i].kl]=1;
}
for(auto it : num) {
for(ll i=0;i<=n;i++) {
f[it][sum[i]%it].push_back(i);
}
}
s=read();
for(ll i=1;i<=m;i++) {
ll l=b[i].l,r=b[i].r,kl=b[i].kl;
bool fl=0;
for(ll j=0;j<kl;j++) {
ll pl=0,pr=f[kl][j].size()-1,cntl=-1,cntr=-1;
while(pl<=pr) {
ll mid=(pl+pr>>1);
if(f[kl][j][mid]>=l-1) {
cntl=mid;
pr=mid-1;
}
else {
pl=mid+1;
}
}
pl=cntl+1,pr=f[kl][j].size()-1;
while(pl<=pr) {
ll mid=(pl+pr>>1);
if(f[kl][j][mid]<=r) {
cntr=mid;
pl=mid+1;
}
else {
pr=mid-1;
}
}
if(cntr-cntl>=1&&cntl>=0&&cntr>=0) {
fl=1;
break;
}
}
if(fl) {
s+=b[i].wl;
}
else {
s-=b[i].wl;
}
}
print(s);
}
praise_long_long main() {
// freopen("toy.in","r",stdin);
// freopen("toy.out","w",stdout);
ll T=1;
// T=read();
while(T--) {
solve();
}
return 0;
}
/**/
B - 序列
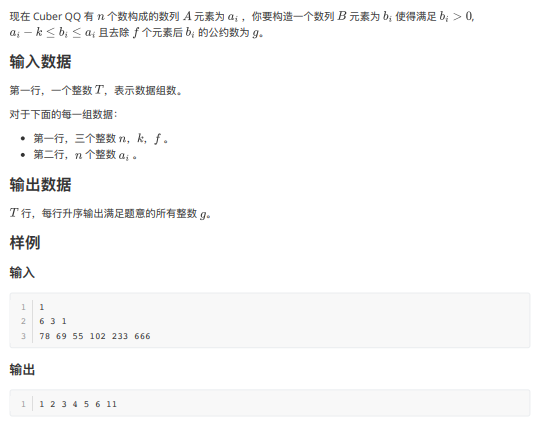
先把每种时间有几个 \(a_i\) 统计出来,做一遍前缀和,那么对于每个 \(g\) 合法的 \(a_i\) 区间是类似于 \([g, g + k] \cup [2g, 2g + k] \dots\) 的区间,所以可以利用前缀和和差分来实现。
时间复杂度:\(O(A \ln A)\),其中 \(A\) 为 \(a_i\) 的最大值。
Code
#include <bits/stdc++.h>
#define pll pair<ll,ll>
#define pld pair<ld,ld>
typedef long long ll;
typedef long double ld;
typedef int praise_long_long;
namespace io {
using namespace std;
inline ll read() {
char x=getchar();
ll ans=0,f=1;
while(x<'0'||x>'9') {
if(x=='-') {
f*=(-1);
}
x=getchar();
}
while(x>='0'&&x<='9') {
ans*=10;
ans+=(x-'0');
x=getchar();
}
return ans*f;
}
inline void print(ll x) {
if(x<0) {
putchar('-');
x=-x;
}
if(x>=10) {
print(x/10);
putchar(x%10+'0');
}
else {
putchar(x+'0');
}
}
}
using namespace io;
const ll N=2e6+5,mod=1e9+7,inf=2e18;
const ld eps=1e-6;
ll n,kl,f,a[N],mx,sum[N],num[N];
vector<ll> ans;
inline void solve() {
n=read(),kl=read(),f=read();
ans.clear();
mx=0;
memset(sum,0,sizeof(sum));
memset(num,0,sizeof(num));
for(ll i=1;i<=n;i++) {
a[i]=read();
mx=max(mx,a[i]);
num[a[i]]++;
sum[max(1ll,a[i]-kl)]++;
sum[a[i]+1]--;
}
for(ll i=1;i<=mx;i++) {
num[i]+=num[i-1];
sum[i]+=sum[i-1];
}
for(ll i=1;i<=mx;i++) {
if(i<=kl) {
if(num[mx]-num[i-1]>=n-f) {
ans.push_back(i);
}
}
else {
ll cnt=0,numl=i;
while(numl<=mx) {
cnt+=sum[numl];
numl+=i;
}
if(cnt>=n-f) {
ans.push_back(i);
}
}
}
for(auto it : ans) {
print(it);
putchar(' ');
}
puts("");
}
praise_long_long main() {
// freopen("seq.in","r",stdin);
// freopen("seq.out","w",stdout);
ll T=1;
T=read();
while(T--) {
solve();
}
return 0;
}
/**/
C - 文件
鄙人在洛谷上写了篇题解,这里直接复制。
暴力
事实上暴力十分简单,在每次交换时只是交换位置的话会更快一些。
时间复杂度:\(O(q\times n \times m)\)。
Code
#include <bits/stdc++.h>
#define pll pair<ll,ll>
#define pld pair<ld,ld>
typedef long long ll;
typedef long double ld;
typedef int praise_long_long;
namespace io {
using namespace std;
inline ll read() {
char x=getchar();
ll ans=0,f=1;
while(x<'0'||x>'9') {
if(x=='-') {
f*=(-1);
}
x=getchar();
}
while(x>='0'&&x<='9') {
ans*=10;
ans+=(x-'0');
x=getchar();
}
return ans*f;
}
inline void print(ll x) {
if(x<0) {
putchar('-');
x=-x;
}
if(x>=10) {
print(x/10);
putchar(x%10+'0');
}
else {
putchar(x+'0');
}
}
}
using namespace io;
const ll N=1e3+5,mod=1e9+7,inf=2e18;
const ld eps=1e-6;
ll num[N][N],n,m,q;
pll kl[N][N];
string a[N][N];
inline void solve() {
cin>>n>>m>>q;
for(ll i=1;i<=n;i++) {
for(ll j=1;j<=m;j++) {
cin>>a[i][j];
num[i][j]=(i-1)*m+j;
}
}
while(q--) {
ll x,y,xl,yl,len,cl;
cin>>x>>y>>xl>>yl>>len>>cl;
for(ll i=0;i<len;i++) {
for(ll j=0;j<cl;j++) {
swap(num[x+i][y+j],num[xl+i][yl+j]);
}
}
}
for(ll i=1;i<=n;i++) {
for(ll j=1;j<=m;j++) {
ll num1=num[i][j]%m,num2=(num[i][j]-num1)/m+1;
if(num1==0) {
num2--;
num1+=m;
}
cout<<a[num2][num1]<<' ';
}
cout<<'\n';
}
}
praise_long_long main() {
// freopen("file.in","r",stdin);
// freopen("file.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
ll T=1;
// T=read();
while(T--) {
solve();
}
return 0;
}
/**/
正解
我们可以想象一下,每次只交换两个不相交的两个相同长宽的矩形就像不像在一块布上剪下两块交换后缝好?
不难发现,如果能够只在四边进行操作,而不在内部每一个点上进行转换,时间复杂度会大大降低,但什么数据结构能够在 \(O(1)\) 的复杂度内大面积交换呢?
如果是一维的转换我们可以想到链表,那么二维转换我们可以想到四向链表,在每次访问时只需要修改四周指向的位置,时间复杂度就减下来了。
时间复杂度:\(O(q \times (n+m))\)。
Code
#include <bits/stdc++.h>
#define pll pair<ll,ll>
#define pld pair<ld,ld>
typedef long long ll;
typedef long double ld;
typedef int praise_long_long;
namespace io {
using namespace std;
inline ll read() {
char x=getchar();
ll ans=0,f=1;
while(x<'0'||x>'9') {
if(x=='-') {
f*=(-1);
}
x=getchar();
}
while(x>='0'&&x<='9') {
ans*=10;
ans+=(x-'0');
x=getchar();
}
return ans*f;
}
inline void print(ll x) {
if(x<0) {
putchar('-');
x=-x;
}
if(x>=10) {
print(x/10);
putchar(x%10+'0');
}
else {
putchar(x+'0');
}
}
}
using namespace io;
const ll N=1e3+5,mod=1e9+7,inf=2e18;
const ld eps=1e-6;
struct List {
ll left,right,up,down,val;
} lst[N*N];
ll n,m,q;
string a[N][N];
inline void insert(ll val) {
ll num=val%(m+2),numl=val/(m+2);
ll up=(numl-1)*(m+2)+num,down=(numl+1)*(m+2)+num,left=val-1,right=val+1;
lst[val]={left,right,up,down,val};
}
inline ll find(ll rt,ll sp) {
for(ll i=lst[rt].right;;i=lst[i].right) {
sp--;
if(!sp) {
return lst[i].val;
}
}
return 0;
}
inline void query(ll x,ll y,ll xl,ll yl,ll len,ll cl) {
ll num=find(x*(m+2),y),numl=find(xl*(m+2),yl);
ll kl=num,kll=numl;
for(ll i=1;i<=len;i++) {
ll p1=lst[kl].left,p2=lst[kll].left;
swap(lst[p1].right,lst[p2].right);
swap(lst[kl].left,lst[kll].left);
if(i==len) {
break;
}
kl=lst[kl].down,kll=lst[kll].down;
}
for(ll i=1;i<=cl;i++) {
ll p1=lst[kl].down,p2=lst[kll].down;
swap(lst[p1].up,lst[p2].up);
swap(lst[kl].down,lst[kll].down);
if(i==cl) {
break;
}
kl=lst[kl].right,kll=lst[kll].right;
}
for(ll i=1;i<=len;i++) {
ll p1=lst[kl].right,p2=lst[kll].right;
swap(lst[p1].left,lst[p2].left);
swap(lst[kl].right,lst[kll].right);
if(i==len) {
break;
}
kl=lst[kl].up,kll=lst[kll].up;
}
for(ll i=1;i<=cl;i++) {
ll p1=lst[kl].up,p2=lst[kll].up;
swap(lst[p1].down,lst[p2].down);
swap(lst[kl].up,lst[kll].up);
if(i==cl) {
break;
}
kl=lst[kl].left,kll=lst[kll].left;
}
}
inline void output(ll x) {
for(ll i=lst[x].right;i!=x+m+1;i=lst[i].right) {
ll xl=(lst[i].val)/(m+2),yl=(lst[i].val)%(m+2);
cout<<a[xl][yl]<<' ';
}
cout<<'\n';
}
inline void solve() {
cin>>n>>m>>q;
for(ll i=1;i<=m;i++) {
lst[(n+1)*(m+2)+i]={0,0,n*(m+2)+i,0,(n+1)*(m+2)+i};
lst[i]={0,0,0,m+2+i,i};
}
for(ll i=1;i<=n;i++) {
lst[i*(m+2)]={0,i*(m+2)+1,0,0,i*(m+2)};
lst[i*(m+2)+m+1]={i*(m+2)+m,0,0,i*(m+2)+m+1};
}
for(ll i=1;i<=n;i++) {
for(ll j=1;j<=m;j++) {
cin>>a[i][j];
insert(i*(m+2)+j);
}
}
while(q--) {
ll x,y,xl,yl,len,cl;
cin>>x>>y>>xl>>yl>>len>>cl;
query(x,y,xl,yl,len,cl);
}
for(ll i=1;i<=n;i++) {
output(i*(m+2));
}
}
praise_long_long main() {
// freopen("file.in","r",stdin);
// freopen("file.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);
ll T=1;
// T=read();
while(T--) {
solve();
}
return 0;
}
/**/
D - 排列
事实上我们可以考虑先想一下简化版,假设每个约束条件为 \(b\) 强制在 \(a\) 的后面,\(c\) 强制在 \(b\) 的后面,与原题区别在于强制要求了 \(a,c\) 的顺序。那么这道题就变成了拓扑排序的板子题,因为保证存在解,又给定了顺序,因此直接拓扑即可。
现在重新考虑一下这道题,由于每个约束条件 \(a,c\) 的地位一模一样,因此我们将他们称为 \(e\),将 \(b\) 成为 \(m\),此时一个约束条件的在序列中的出现情况共有3种:\(eem,eme,mee\) 但是只有第二种情况时该约束条件才会产生1的贡献,由于三种条件太复杂,我们又发现 \(mee\) 这种情况可以通过类似于刚才的拓扑排序直接跳过不会出现,也就是说我们可以先保证每一个 \(m\) 都不会在两个 \(e\) 都没出现的时候出现。具体地,我们对于每一个条件,将两个 \(e\) 同时向 \(m\) 连边,当删除其中一条边时,同时删除另一条,这样虽然图建出来可能有环,但题目保证有解,因此一定存在合法拓扑序,这样删边也就能同时拆环了。
Code
#include <bits/stdc++.h>
#define pll pair<ll,ll>
#define pld pair<ld,ld>
typedef long long ll;
typedef long double ld;
typedef int praise_long_long;
namespace io {
using namespace std;
inline ll read() {
char x=getchar();
ll ans=0,f=1;
while(x<'0'||x>'9') {
if(x=='-') {
f*=(-1);
}
x=getchar();
}
while(x>='0'&&x<='9') {
ans*=10;
ans+=(x-'0');
x=getchar();
}
return ans*f;
}
inline void print(ll x) {
if(x<0) {
putchar('-');
x=-x;
}
if(x>=10) {
print(x/10);
putchar(x%10+'0');
}
else {
putchar(x+'0');
}
}
}
using namespace io;
const ll N=1e5+5,mod=1e9+7,inf=2e18;
const ld eps=1e-6;
struct node {
ll al,bl,cl;
} a[N];
ll n,m,du[N],l=1,r,ans[N],vis[N];
vector<pll> g[N];
vector<ll> v[N];
queue<ll> q;
inline void tosort() {
for(ll i=1;i<=n;i++) {
if(!du[i]) {
q.push(i);
}
}
while(!q.empty()) {
ll d=q.front();
q.pop();
ll val1=0,val2=0;
for(auto it : g[d]) {
ll al=it.first,cl=it.second;
if(vis[al]&&vis[cl]) {
continue;
}
if(vis[al]) {
if(vis[al]<=l) {
val1++;
}
if(vis[al]>=r) {
val2++;
}
}
if(vis[cl]) {
if(vis[cl]<=l) {
val1++;
}
if(vis[cl]>=r) {
val2++;
}
}
}
for(auto it : v[d]) {
ll al=a[it].al,bl=a[it].bl,cl=a[it].cl;
if(vis[al]) {
if(!vis[bl]) {
if(vis[al]<=l) {
val2++;
}
if(vis[al]>=r) {
val1++;
}
}
}
if(vis[cl]) {
if(!vis[bl]) {
if(vis[cl]<=l) {
val2++;
}
if(vis[cl]>=r) {
val1++;
}
}
}
if(!vis[al]&&!vis[cl]) {
du[bl]--;
if(!du[bl]) {
q.push(bl);
}
}
}
if(val1>=val2) {
vis[d]=l;
l++;
}
else {
vis[d]=r;
r--;
}
if(l>r) {
break;
}
}
}
inline void solve() {
r=n=read(),m=read();
for(ll i=1;i<=m;i++) {
a[i]={read(),read(),read()};
v[a[i].al].push_back(i);
v[a[i].cl].push_back(i);
g[a[i].bl].push_back({a[i].al,a[i].cl});
du[a[i].bl]++;
}
tosort();
for(ll i=1;i<=n;i++) {
ans[vis[i]]=i;
}
for(ll i=1;i<=n;i++) {
print(ans[i]);
putchar(' ');
}
}
praise_long_long main() {
// freopen("permutation.in","r",stdin);
// freopen("permutation.out","w",stdout);
ll T=1;
// T=read();
while(T--) {
solve();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号