BLOG-2_JavaHomework_Summary

前言

数学的问题很大，使得PTA的大作业写的并不是很舒服

小总结

把代码比作盖楼的话：

期中考试的题比较舒服，把三道题放一起就知道这是要盖大楼，题之间是循序渐进的，所以每道题还要兼顾可拓展性，于是越写越顺。

而大作业就很难受了，最开始并不知道这是要盖大楼，于是用小平房的代码水了过去，可是楼总是要盖的，于是每次都得拆掉小平房，重新打地基，重新盖房子。

设计与分析

OOP期中考试

第一题

代码

import java.util.Scanner;

public class Main {

       public static void main(String[] args) {
           Scanner in = new Scanner(System.in);
           double x1 = in.nextDouble(), y1 = in.nextDouble(),
                  x2 = in.nextDouble(), y2 = in.nextDouble();
           String colour = in.next();
           Point p1 = new Point(x1, y1), p2 = new Point(x2, y2);
           Line l1 = new Line(p1, p2, colour);
           l1.display();
       }
}

class Point {
       private double x, y;

       public Point(double x, double y) {
           this.x = x;
           this.y = y;
       }

       public void display() {
           Point p = new Point(x, y);
           InputWrong.OutNumLimit(p);
           String s = String.format("(%.2f,%.2f)", x, y);
           System.out.println(s);
       }

       public double getX() {
           return x;
       }

       public double getY() {
           return y;
       }

       public void setX(double x) {
           this.x = x;
       }

       public void setY(double y) {
           this.y = y;
       }
}

class Line {
       private Point p1, p2;
       private String colour;

       public Line(Point p1, Point p2, String colour) {
           this.p1 = p1;
           this.p2 = p2;
           this.colour = colour;
       }

       public double getDistance() {
           return Math.sqrt((p1.getX() - p2.getX()) * (p1.getX() - p2.getX()) + (p1.getY() - p2.getY()) * (p1.getY() - p2.getY()));
       }

       public void display() {
           InputWrong.OutNumLimit(p1, p2);
           System.out.println("The line's color is:" + getColour());
           System.out.println("The line's begin point's Coordinate is:");
           getP1().display();
           System.out.println("The line's end point's Coordinate is:");
           getP2().display();
           System.out.println("The line's length is:" + forMatF(getDistance()));
       }

       private String forMatF(double x) {
           return String.format("%.2f", x);
       }

       public Point getP1() {
           return p1;
       }

       public Point getP2() {
           return p2;
       }

       public String getColour() {
           return colour;
       }

       public void setP1(Point p1) {
           this.p1 = p1;
       }

       public void setP2(Point p2) {
           this.p2 = p2;
       }

       public void setColour(String colour) {
           this.colour = colour;
       }
   }

   class InputWrong {
       public static void OutNumLimit(Point... ps) {
           for (Point i : ps) {
               if ((i.getX() <= 0 || i.getX() > 200) || (i.getY() <= 0 || i.getY() > 200)) {
                   System.out.println("Wrong Format");
                   System.exit(0);
               }
           }
       }
}

类图

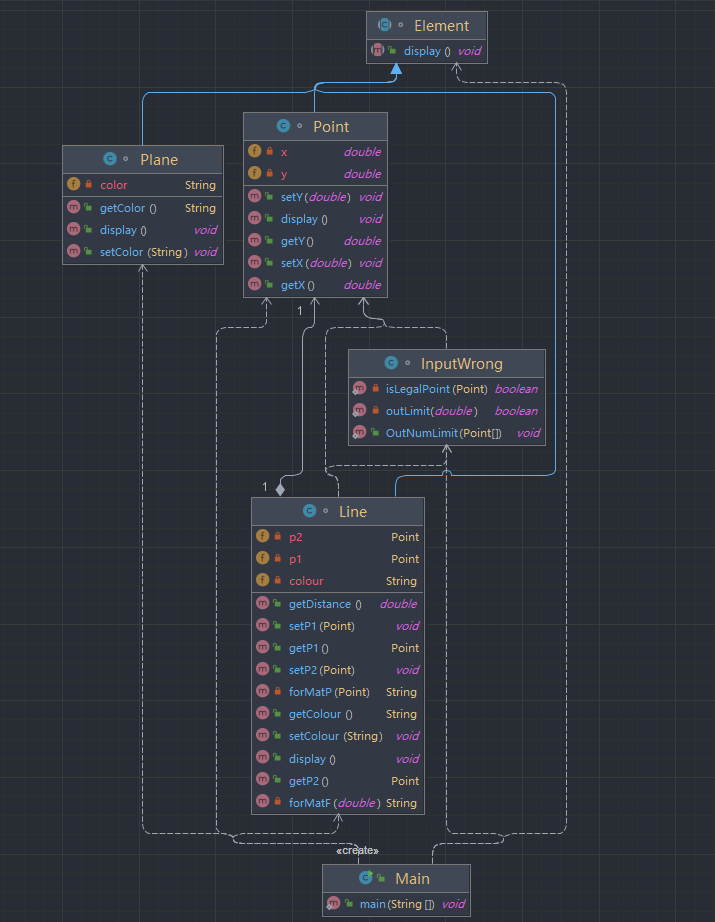
类图解释

Point、Line各自分开实现了display()方法

在Main中实体化了Line和Point并调用了display()

生成报表

分析

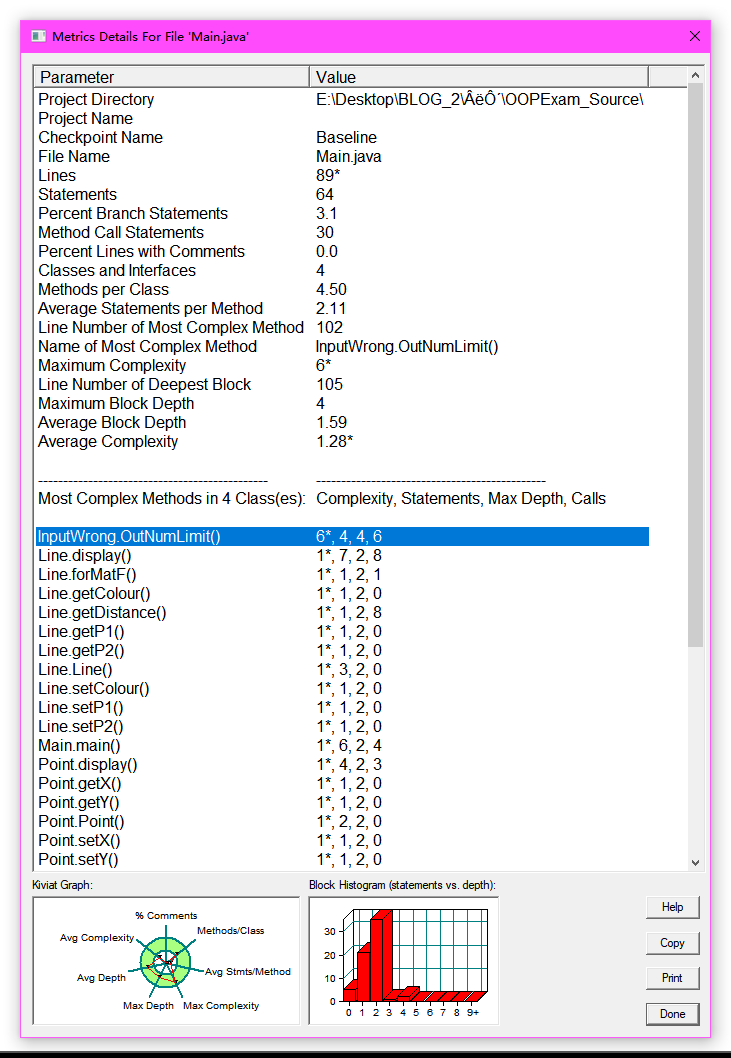
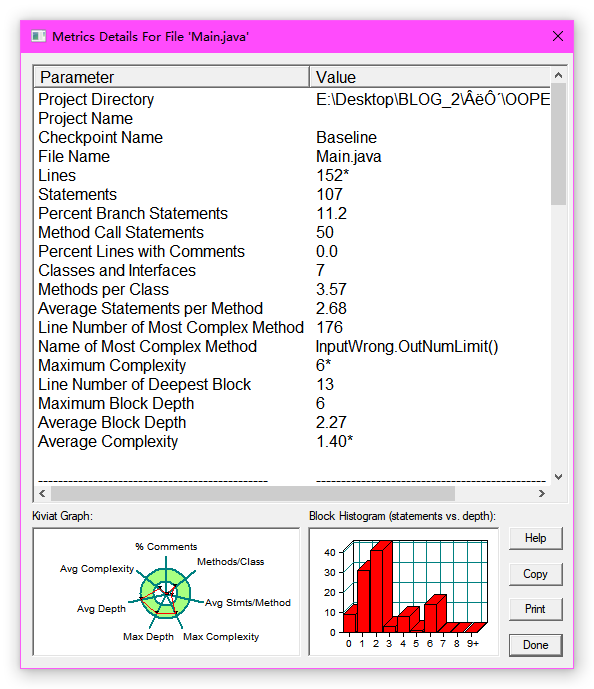
SourceMonitor觉得代码还算合理，各项指标都没有超过绿环

但是最大复杂度仍然很高，可以看到自己写的用来判断输入是否合法的静态方法OutNumLimit.InputWrong()是最复杂的

class InputWrong {
   public static void OutNumLimit(Point... ps) {
       for (Point i : ps) {
           if ((i.getX() <= 0 || i.getX() > 200) || (i.getY() <= 0 || i.getY() > 200)) {
               System.out.println("Wrong Format");
               System.exit(0);
           }
       }
   }
}

改动之后:

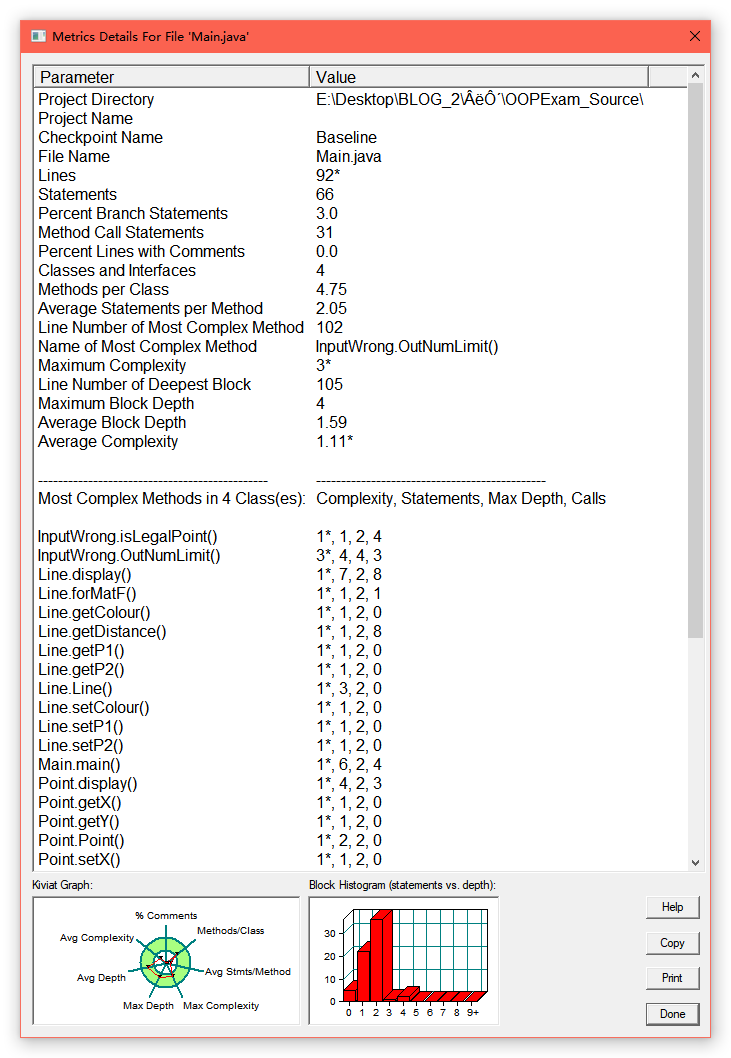
class InputWrong {
   public static void OutNumLimit(Point... ps) {
       for (Point i : ps) {
           if (InputWrong.isLegalPoint(i)) {
               System.out.println("Wrong Format");
               System.exit(0);
           }
       }
   }

   private static boolean isLegalPoint(Point point) {
       return (point.getX() <= 0 || point.getX() > 200) || (point.getY() <= 0 || point.getY() > 200);
   }
}

效果图

复杂度降低了好多！

还可以继续优化

class InputWrong {
   public static void OutNumLimit(Point... ps) {
       for (Point i : ps) {
           if (InputWrong.isLegalPoint(i)) {
               System.out.println("Wrong Format");
               System.exit(0);
           }
       }
   }

   private static boolean isLegalPoint(Point point) {
       return outLimit(point.getX()) || outLimit(point.getY());
   }

   private static boolean outLimit(double location) {
       return location <= 0 || location > 200;
   }
}

快成逆向优化了....

第二题

代码

import java.util.Scanner;

public class Main {

   public static void main(String[] args) {
       Scanner in = new Scanner(System.in);
       double x1 = in.nextDouble(), y1 = in.nextDouble(),
               x2 = in.nextDouble(), y2 = in.nextDouble();
       String colour = in.next();
       Point p1 = new Point(x1, y1), p2 = new Point(x2, y2);
       Line l1 = new Line(p1, p2, colour);
       Plane pl1 = new Plane(colour);
       InputWrong.OutNumLimit(p1, p2);
       Element element = p1;
       p1.display();
       element = p2;
       p2.display();
       element = l1;
       l1.display();
       element = pl1;
       pl1.display();
   }
}

abstract class Element {
   public abstract void display();
}

class Point extends Element {
   private double x, y;

   public Point(double x, double y) {
       this.x = x;
       this.y = y;
   }

   public void display() {
       Point p = new Point(x, y);
       String s = String.format("(%.2f,%.2f)", x, y);
       System.out.println(s);
   }

   public double getX() {
       return x;
   }

   public double getY() {
       return y;
   }

   public void setX(double x) {
       this.x = x;
   }

   public void setY(double y) {
       this.y = y;
   }
}

class Line extends Element {
   private Point p1, p2;
   private String colour;

   public Line(Point p1, Point p2, String colour) {
       this.p1 = p1;
       this.p2 = p2;
       this.colour = colour;
   }

   public double getDistance() {
       return Math.sqrt((p1.getX() - p2.getX()) * (p1.getX() - p2.getX()) + (p1.getY() - p2.getY()) * (p1.getY() - p2.getY()));
   }

   public void display() {
       InputWrong.OutNumLimit(p1, p2);
       System.out.println("The line's color is:" + getColour());
       System.out.println("The line's begin point's Coordinate is:");
       getP1().display();
       System.out.println("The line's end point's Coordinate is:");
       getP2().display();
       System.out.println("The line's length is:" + forMatF(getDistance()));
   }

   private String forMatF(double x) {
       return String.format("%.2f", x);
   }

   private String forMatP(Point p) {
       return String.format("(%.2f,%.2f)", p.getX(), p.getY());
   }

   public Point getP1() {
       return p1;
   }

   public Point getP2() {
       return p2;
   }

   public String getColour() {
       return colour;
   }

   public void setP1(Point p1) {
       this.p1 = p1;
   }

   public void setP2(Point p2) {
       this.p2 = p2;
   }

   public void setColour(String colour) {
       this.colour = colour;
   }
}

class Plane extends Element {
   private String color;

   public Plane(String color) {
       this.color = color;
   }

   public void display() {
       System.out.println("The Plane's color is:" + getColor());
   }

   public String getColor() {
       return color;
   }

   public void setColor(String color) {
       this.color = color;
   }
}

class InputWrong {
   public static void OutNumLimit(Point... ps) {
       for (Point i : ps) {
           if (InputWrong.isLegalPoint(i)) {
               System.out.println("Wrong Format");
               System.exit(0);
           }
       }
   }

   private static boolean isLegalPoint(Point point) {
       return outLimit(point.getX()) || outLimit(point.getY());
   }

   private static boolean outLimit(double location) {
       return location <= 0 || location > 200;
   }
}

类图

类图解释

Point、Line、Plane、继承自抽象类Element,并且都为各自实现了display()方法
Main将Point、Line、Plane实体化

生成报表

分析

之前最复杂的代码段进行优化后，可以看到SourceMonitor也在夸我们的代码写的好

第三题

代码

import java.util.ArrayList;
import java.util.Scanner;

public class Main {

   public static void main(String[] args) {
       Scanner in = new Scanner(System.in);
       GeometryObject geometryObject = new GeometryObject();
       int choice = in.nextInt();
       while (choice != 0) {
           switch (choice) {
               case 1: {
                   Point p = new Point(in.nextDouble(), in.nextDouble());
                   InputWrong.OutNumLimit(p);
                   geometryObject.add(p);
                   break;
               }
               case 2: {
                   Point p1 = new Point(in.nextDouble(), in.nextDouble());
                   Point p2 = new Point(in.nextDouble(), in.nextDouble());
                   String colour = in.next();
                   InputWrong.OutNumLimit(p1, p2);
                   Line line = new Line(p1, p2, colour);
                   geometryObject.add(line);
                   break;
               }
               case 3: {
                   String colour = in.next();
                   Plane pl1 = new Plane(colour);
                   geometryObject.add(pl1);
                   break;
               }
               case 4: {
                   int x = in.nextInt();
                   geometryObject.delete(x - 1);
                   break;
               }
           }
           choice = in.nextInt();
       }
       geometryObject.display();
   }
}

class GeometryObject {
   private ArrayList<Element> elementArrayList = new ArrayList<>();

   public void add(Element element) {
       elementArrayList.add(element);
   }

   public void delete(int index) {
       for (int i = 0; i < elementArrayList.size(); i++) {
           if (i == index) {
               elementArrayList.remove(i);
               break;
           }
       }
   }

   public void display() {
       for (Element e : elementArrayList) e.display();
   }

}

abstract class Element {
   public abstract void display();
}

class Point extends Element {
   private double x, y;

   public Point(double x, double y) {
       this.x = x;
       this.y = y;
   }

   public void display() {
       Point p = new Point(x, y);
       String s = String.format("(%.2f,%.2f)", x, y);
       System.out.println(s);
   }

   public double getX() {
       return x;
   }

   public double getY() {
       return y;
   }

   public void setX(double x) {
       this.x = x;
   }

   public void setY(double y) {
       this.y = y;
   }
}

class Line extends Element {
   private Point p1, p2;
   private String colour;

   public Line(Point p1, Point p2, String colour) {
       this.p1 = p1;
       this.p2 = p2;
       this.colour = colour;
   }

   public double getDistance() {
       return Math.sqrt((p1.getX() - p2.getX()) * (p1.getX() - p2.getX()) + (p1.getY() - p2.getY()) * (p1.getY() - p2.getY()));
   }

   public void display() {
       InputWrong.OutNumLimit(p1, p2);
       System.out.println("The line's color is:" + getColour());
       System.out.println("The line's begin point's Coordinate is:");
       getP1().display();
       System.out.println("The line's end point's Coordinate is:");
       getP2().display();
       System.out.println("The line's length is:" + forMatF(getDistance()));
   }

   private String forMatF(double x) {
       return String.format("%.2f", x);
   }

   public Point getP1() {
       return p1;
   }

   public Point getP2() {
       return p2;
   }

   public String getColour() {
       return colour;
   }

   public void setP1(Point p1) {
       this.p1 = p1;
   }

   public void setP2(Point p2) {
       this.p2 = p2;
   }

   public void setColour(String colour) {
       this.colour = colour;
   }
}

class Plane extends Element {
   private String color;

   public Plane(String color) {
       this.color = color;
   }

   public void display() {
       System.out.println("The Plane's color is:" + getColor());
   }

   public String getColor() {
       return color;
   }

   public void setColor(String color) {
       this.color = color;
   }
}

class InputWrong {
   public static void OutNumLimit(Point... ps) {
       for (Point i : ps) {
           if ((i.getX() <= 0 || i.getX() > 200) || (i.getY() <= 0 || i.getY() > 200)) {
               System.out.println("Wrong Format");
               System.exit(0);
           }
       }
   }
}

类图

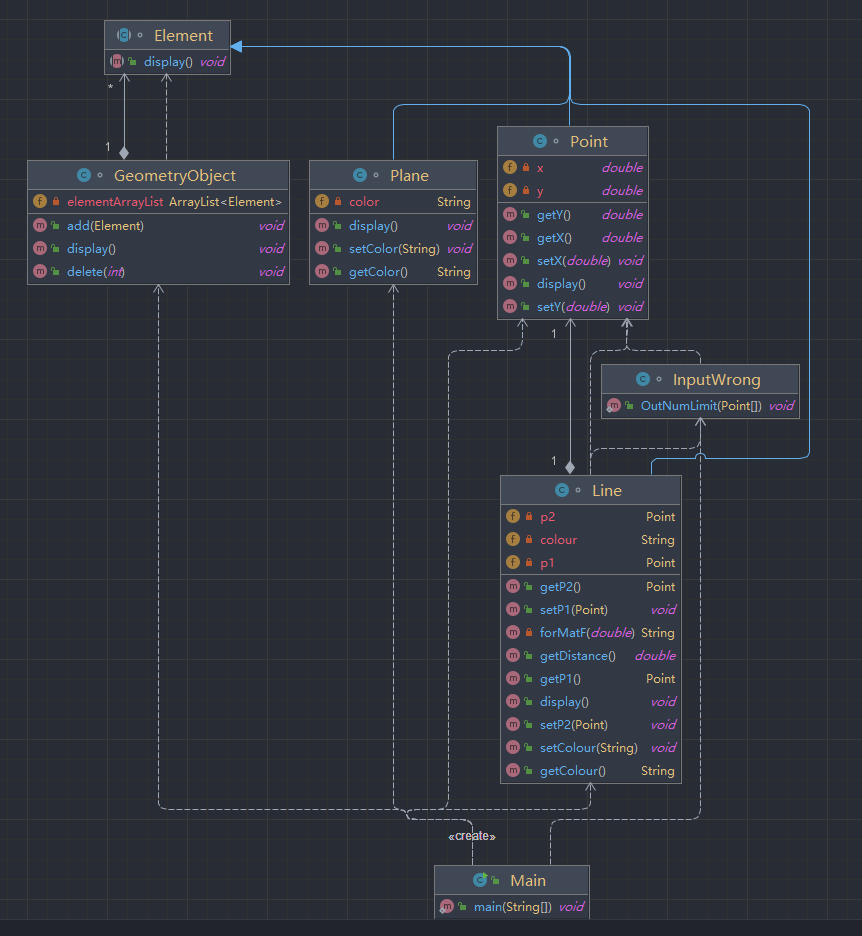
类图解释

Point、Line、Plane、继承自抽象类Element,并且都为各自实现了display()方法

GeometryObject用来收集存储和修改集合对象

Main将GeometryObject、Point、Line、Plane实体化

生成报表

分析

SourceMonitor仍然觉得代码还算合理，各项指标都没有超过绿环

最复杂的函数名是 InputWrong.OutNumLimit(); 也就比System.out.println()多几个字母！

PTA_4

第一题

正则表达式：

题目太长，简言之就是，从若干行的文章中提取每行数字之和

代码

import java.util.Scanner;
import java.util.regex.Matcher;
import java.util.regex.Pattern;

public class Main {
       public static void main(String[] args) {
           Scanner in = new Scanner(System.in);
           String s;
           while (in.hasNext()) {
               s = in.nextLine();
               if (s.equals("end")) break;
               System.out.println(toSum(toNums(toStrs(s))));
           }
       }

       public static String[] toStrs(String s) {
           String[] nums = new String[10];
           int cnt = 0;
           Matcher readNum = Pattern.compile("(\\d+)").matcher(s);
           int readNum_start = 0;
           while (readNum.find(readNum_start)) {
               nums[cnt++] = readNum.group(1);
               readNum_start = readNum.end();
           }
           return nums;
       }

       public static long[] toNums(String[] s) {
           long[] nums = new long[10];
           for (int i = 0; i < s.length && s[i] != null; i++) {
               nums[i] = Long.parseLong(s[i]);
           }
           return nums;
       }

       public static long toSum(long[] nums) {
           long sum = 0;
           for (long i : nums) sum += i;
           return sum;
       }
}

正则表达式的基本应用

第二题

import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Scanner;

public class Main {
   public static void main(String[] args) {
       Scanner in = new Scanner(System.in);
       String input = in.nextLine();
       InputData data = new InputData();
       ParseInput.paseInput(input, data);
       switch (ParseInput.getChoice(input)) {
           case 1: {
               PointInputError.wrongNumberOfPoints(data.getPoints(), 4);   //wrong number of points
               ArrayList<Point> points = data.getPoints();
               Quadrilateral S = new Quadrilateral(points);
               S.isCoincident();   //points coincide
               System.out.println(S.isQuadrilateral() + " " + S.isParallelogram());
               break;
           }
           case 2: {
               PointInputError.wrongNumberOfPoints(data.getPoints(), 4);
               ArrayList<Point> points = data.getPoints();
               Quadrilateral S = new Quadrilateral(points);
               if (S.isQuadrilateral()) {
                   S.isCoincident();System.out.println(S.isRhombus() + " " + S.isRectangle() + " " + S.isQuadrate());
               }
               else System.out.println("not a quadrilateral");
               break;
           }
           case 3: {
               PointInputError.wrongNumberOfPoints(data.getPoints(), 4);
               ArrayList<Point> points = data.getPoints();
               Quadrilateral S = new Quadrilateral(points);
               if (S.isQuadrilateral()){   //是四边形
                   S.isCoincident();System.out.println(S.isTu() + " " + OutFormat.doubleFormat(S.getPerimeter()) + " " + OutFormat.doubleFormat(S.getSquare()));
               }
               else System.out.println("not a quadrilateral");
               break;
           }
           case 4: {
               System.out.println("not a quadrilateral or triangle");
               System.exit(0);
           }
           case 5: {
                       System.out.println("in the quadrilateral");
                       System.exit(0);
           }
       }
   }


}

class Shapes{

   private ArrayList<Point> ps;

   public Shapes() {
   }
   public Shapes(ArrayList<Point> ps) {
       this.ps = ps;
//        ShapeInputError.shapeInputError(ps);
   }
   public ArrayList<Point> getPs() {
       return ps;
   }

   // 获取四边形周长
   public double getPerimeter() {
       double sum = 0;
       for (int i = 0; i < 4; i++) {
           sum += Point.getDistance(ps.get(i), ps.get((i + 1) % 4));
       }
       return sum;
   }

   // 获取四边形的面积
   public double getSquare() {
       if (isTu()) {
           return getTriangleSquare(ps.get(0), ps.get(1), ps.get(2)) + getTriangleSquare(ps.get(0), ps.get(3), ps.get(2));
       } else {
           return Math.min(
                   getTriangleSquare(ps.get(0), ps.get(1), ps.get(2)) + getTriangleSquare(ps.get(2), ps.get(3), ps.get(0)),
                   getTriangleSquare(ps.get(1), ps.get(2), ps.get(3)) + getTriangleSquare(ps.get(3), ps.get(0), ps.get(1))
           );
           // 0 1 2 ,2 3 0
           // 1 2 3 ,3 0 1
       }
   }
   // 向量求三角形面积
   public static double getTriangleSquare(Point a, Point b, Point c) {
       double x1 = a.getX() - b.getX();
       double x2 = a.getX() - c.getX();
       double y1 = a.getY() - b.getY();
       double y2 = a.getY() - c.getY();
       return Math.abs(x1 * y2 - x2 * y1) / 2.0;
   }

   // 是否为四边形
   public boolean isQuadrilateral() {
       return !eveCoincide();
   }

   public boolean is3D(){//有交点点在边上
       Line[] ls = getSideline();
       if(isOnTheEdge(ls[0].getIntersection(ls[2])))return true;
       if(isOnTheEdge(ls[1].getIntersection(ls[3])))return true;
       return false;
   }

   // 是否为平行四边形
   public boolean isParallelogram() {
       if (!isQuadrilateral()) return false;
       for (int i = 0; i < 2; i++) {
           Line l1 = new Line(ps.get(i), ps.get(i + 1));
           Line l2 = new Line(ps.get(i + 2), ps.get((i + 3) % 4));
           if (!l1.isParallel(l2)) return false;
       }
       return true;
   }

   //是否为菱形
   public boolean isRhombus() {
       if (!isParallelogram()) return false;
       for (int i = 0; i < 2; i++) {
           Line l1 = new Line(ps.get(i), ps.get(i + 1));
           Line l2 = new Line(ps.get(i + 2), ps.get((i + 3) % 4));
           if (Math.abs(l1.getDistance() - l2.getDistance()) < 0.001) return true;
       }
       return false;
   }

   // 是否为矩形
   public boolean isRectangle() {
       if (!isParallelogram()) return false;
       Line l1 = new Line(ps.get(0), ps.get(1));
       Line l2 = new Line(ps.get(0), ps.get(3));
       return (Math.abs(l1.getAngle(l2) - 90) < 0.001);
   }

   // 是正方形
   public boolean isQuadrate() {
       return isRhombus() && isRectangle();
   }

   // 是凸四边形
   public boolean isTu() {
       if (!isQuadrilateral()) return false;
       return Math.abs((getTriangleSquare(ps.get(0), ps.get(1), ps.get(2)) + getTriangleSquare(ps.get(2), ps.get(3), ps.get(0)))
               - (getTriangleSquare(ps.get(1), ps.get(2), ps.get(3)) + getTriangleSquare(ps.get(3), ps.get(0), ps.get(1))))
               < 0.0001;
   }

   // 判断所有点是否有三点共线
   public boolean eveCoincide() {
       return (isCoincide(ps.get(0), ps.get(1), ps.get(2))
               || isCoincide(ps.get(0), ps.get(1), ps.get(3))
               || isCoincide(ps.get(0), ps.get(2), ps.get(3))
               || isCoincide(ps.get(1), ps.get(2), ps.get(3))
       );
   }

   // 判断三个点是否有三点共线
   private boolean isCoincide(Point a, Point b, Point c) {
       Line l1 = new Line(a, b);
       return l1.isOnline(c);
   }

   // 判断是否有重合
   public void isCoincident() {
       for (int i = 0; i < 3; i++) {
           for (int j = i + 1; j < 4; j++) {
               if (haveCoincident(ps.get(i), ps.get(j))) {
                   System.out.println("points coincide");
                   System.exit(0);
               }
           }
       }
   }

   // 判断某两点是否重合
   private static boolean haveCoincident(Point p1, Point p2) {
       return (p1.getX() == p2.getX() && p1.getY() == p2.getY());
   }

   /* 判断x\y\z三个点的坐标是否能构成一个三角形 */
   public boolean isTriangle() {
       return false;
   }

   public Line[] getSideline() {
       ArrayList<Point> ps = getPs();
       Line[] ls = new Line[ps.size()];
       for(int i=0;i<ps.size();i++){
           Line l1 = new Line(ps.get(i),ps.get((i+1)%(ps.size())));
           ls[i]= l1;
       }
       return ls;
   }

   /* 获取三角形的面积，此处采用海伦公式 */
   public double getArea() {
       return 0;
   }

   //判断点p是否本三角形的顶点
   public boolean isVertex(Point p) {
       for(Point pp : ps)if(p.equals(pp))return true;
//        return p.equals(x) || p.equals(y) || p.equals(z);
       return false;
   }



   // 获取直线l与三角形的交点，如果没有，数组为空。
   public ArrayList<Point> getIntersections(Line l) {
       ArrayList<Point> pointsInter = new ArrayList<>();
       Line[] lines = getSideline();
       for (Line i : lines)if(l.isCoincide(i))return null;
       for (Line i : lines){
           pointsInter.add(i.getIntersection(l));//getIntersection//getCrossPoint
       }
       return pointsInter;
   }

   /*
    * 计算三角形上两个点所切分出的两个区域的面积。
    * 输入：在三角形三条边上的两个点，要求都不为null，且不在同一条边。
    *       输入为null将会导致异常。
    * 输出：两部分的面积，并按小-大的顺序排序。
    */
   public double[] calArea(Point p1, Point p2) {
       return null;
   }

   /* 计算三角形和本三角形的面积差
    * 输入：一个三角形	，输入约束：输入的三角形是本三角形切割下来的一个部分
    * 计算：本三角形面积减去输入的三角形面积
    * 输出：三角形相减后剩余部分的面积
    */
   public double calAreaDiffrence(Triangle t1) {
       double area = t1.getArea();
       area = getArea() - area;
       return area;
   }

   // 判断线是否与三角形的某条边重合
   public boolean judgeLineCoincide(Line l) {
       for(Line ls : getSideline())if(l.isCoincide(ls))return true;
       return false;
   }

   /*
    * 输入：点p
    * 输出：p是否在本三角形的三条边线（不含顶点）上。在线上输出true，否则输出false。
    */
   public boolean isOnTheEdge(Point p) {
       for(Line ls : getSideline())
           if(ls.isOnline(p)&&!p.equals(ls.getPointA())&&!p.equals(ls.getPointB()))
               return true;
       return false;
   }

}

class Point {
   public double x;
   public double y;

   public Point(double x, double y) {
       this.x = x;
       this.y = y;
   }

   public Point() {

   }

   /* 设置坐标x，将输入参数赋值给属性x */
   public void setX(double x) {
       this.x = x;
   }

   /* 设置坐标y，将输入参数赋值给属性y */
   public void setY(double y) {
       this.y = y;
   }

   /* 获取坐标x，返回属性x的值 */
   public double getX() {
       return x;
   }

   /* 获取坐标y，返回属性y的值 */
   public double getY() {
       return y;
   }

   //判断两点是否重合
   public boolean equals(Point p) {
       return this.x == p.getX() && this.y == p.getY();
   }

   public static double getDistance(Point p1, Point p2) {
       return Math.sqrt((p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y));
   }

   public static Point addPoint(Point p1, Point p2){
       return new Point(p1.getX()+p2.getX(),p1.getY()+p2.getY());
   }

   public static Point jianPoint(Point p1, Point p2){
       return new Point(p1.getX()-p2.getX(),p1.getY()-p2.getY());
   }

   public static Point chengPoint(Point p1, double t){
       return new Point(p1.getX()*t,p1.getY()*t);
   }
}

class PointInputError {
   //判断从字符串中解析出的点的数量是否合格。
   public static void wrongNumberOfPoints(ArrayList<Point> ps, int num) {
       if (ps.size() != num) {
           System.out.println("wrong number of points");
           System.exit(0);
       }
   }

   //判断输入的字符串中点的坐标部分格式是否合格。若不符合，报错并退出程序
   public static void wrongPointFormat(String s) {
       if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
           System.out.println("Wrong Format");
           System.exit(0);
       }
   }

   // 输入字符串是否是"选项:字符串"格式，选项部分是否是1~4其中之一
   public static void wrongChoice(String s) {
       if (!s.matches("[1-5]:.+")) {
           System.out.println("Wrong Format");
           System.exit(0);
       }
   }
}

class Quadrilateral extends Shapes{

   public Quadrilateral(ArrayList<Point> ps) {
       super(ps);
   }

   /*
    * 判断点p是否在本三角形内部（射线法）
    * 输出：1：在内部，-1：在外部，0：在三角形上
    */
   public int isInside(Point p) {

       if (this.isOnTheEdge(p)) {
           return 0;
       }
       if (isVertex(p)) {
           return 0;
       }
       Point pb;
       Line l;
       if (p.x == 0 && p.y == 0) {
           pb = new Point(0, 1);
       } else {
           pb = new Point(0, 0);
       }
       l = new Line(p, pb);
       ArrayList<Point> ps = this.getIntersections(l);//获取直线与三角形的交点列表
       int num = ps.size();

       if (num == 0||num==1) {
           return -1;
       }
       if(num == 2) {
           Line l1 = new Line(ps.get(0),ps.get(1));
           if(l1.isBetween(p)) {
               return 1;
           }else {
               return -1;
           }
       }
       return 0;
   }

   public static void main(String[] args) {
       Point xxx = new Point(-100,100);
       Point p1 = new Point(0,0);
       Point p2 = new Point(0,100);
       Point p3 = new Point(100,100);
       Point p4 = new Point(100,0);
       ArrayList<Point> ps = new ArrayList<>();
       ps.add(p1);ps.add(p2);ps.add(p3);ps.add(p4);
       Quadrilateral ju = new Quadrilateral(ps);
       System.out.println(ju.isInside(xxx));
   }

}

class Triangle extends Shapes{

   public Triangle(ArrayList<Point> ps) {
       super(ps);
   }

   /*
    * 判断点p是否在本三角形内部（射线法）
    * 输出：1：在内部，-1：在外部，0：在三角形上
    */
   public int isInside(Point p) {
       //int i = 0;
       if (this.isOnTheEdge(p)) {
           return 0;
       }
       if (isVertex(p)) {
           return 0;
       }
       Point pb;
       Line l;
       if (p.x == 0 && p.y == 0) {
           pb = new Point(0, 1);
       } else {
           pb = new Point(0, 0);
       }
       l = new Line(p, pb);
       ArrayList<Point> ps = this.getIntersections(l);//获取直线与三角形的交点列表
       int num = ps.size();
       if (num == 0||num==1) {
           return -1;
       }
       if(num == 2) {
           Line l1 = new Line(ps.get(0),ps.get(1));
           if(l1.isBetween(p)) {
               return 1;
           }else {
               return -1;
           }
       }
       return 0;
   }

}



class InputData {
   private int choice;//用户输入的选择项
   private ArrayList<Point> points = new ArrayList<Point>();//用户输入的点坐标

   public int getChoice() {
       return choice;
   }

   public void setChoice(int choice) {
       this.choice = choice;
   }

   public ArrayList<Point> getPoints() {
       return points;
   }

   public void addPoint(Point p) {
       this.points.add(p);
   }
}

class OutFormat {
   //按要求格式化实数的输出。
   public static Double doubleFormat(double b) {
       DecimalFormat df = new DecimalFormat("#.000");
       return Double.valueOf(df.format(b));
   }
}

class ParseInput {
   /*
    * 输入：完整的输入字符串，包含选项和所有点的信息，格式：选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-5
    * 		一个空InputData对象
    * 处理：将输入字符串中的选项和点信息提取出来并设置到InputData对象中
    * 输出：包含选项值和所有点的Point对象的InputData对象。
    */
   public static void paseInput(String s, InputData d) {
       PointInputError.wrongChoice(s);
       d.setChoice(getChoice(s));
       s = s.substring(2);
       pasePoints(s, d);
   }

   //获取输入字符串（格式：“选项：点坐标”）中选项部分
   public static int getChoice(String s) {
       char c = s.charAt(0);
       return c - 48;
   }

   /*
    * 输入：一个字符串，包含所有点的信息，格式：x1,y1 x2,y2 .....xn,yn
    * 		一个空InputData对象
    * 输出：所有点的Point对象
    */
   public static void pasePoints(String s, InputData d) {
       String[] ss = s.split(" ");
       if (ss.length == 0)
           return;
       for (String value : ss) {
           d.addPoint(readPoint(value));
       }
   }

   /*
    * 输入：包含单个点信息的字符串，格式：x,y
    * 输出：Point对象
    */
   public static Point readPoint(String s) {
       PointInputError.wrongPointFormat(s);
       String[] ss = s.split(",");
       double x = Double.parseDouble(ss[0]);
       double y = Double.parseDouble(ss[1]);
       return new Point(x, y);
   }
}


class Line {
   private Point p1;//线上的第一个点
   private Point p2;//线上的第二个点

   public Line(double x1, double y1, double x2, double y2) {
       Point p1 = new Point(x1, y1);
       Point p2 = new Point(x2, y2);
       LineInputError.pointsCoincideError(p1, p2);//两点是否重合，重合则报错并退出
       this.p1 = p1;
       this.p2 = p2;
   }

   public Line(Point p1, Point p2) {
       LineInputError.pointsCoincideError(p1, p2);//两点是否重合，重合则报错并退出
       this.p1 = p1;
       this.p2 = p2;
   }

   public boolean isBetween(Point x) {
       //System.out.println("isBetween" + " " + this.p1.x + " " + p1.y + " " + p2.x + " " + p2.y + " " + x.x + " " + x.y);
       if (!this.isOnline(x)) {
           return false;
       }

       if (x.equals(p1) || x.equals(p2)) {
           return false;
       }

       double d = Point.getDistance(p1,p2);
       boolean b = Point.getDistance(x,p2) < d && Point.getDistance(x,p1) < d;
       //System.out.println("isBetween" + b);
       return b;
   }

   // 获取直线的长度
   public double getDistance() {
       return Math.sqrt((p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y));
   }

   /* 获取线条的斜率 */
   public Double getSlope() {
       // （x1-x2=0）注意考虑斜率不存在即返回double类型无穷大"Infinite"
       return (p2.getY() - p1.getY()) / (p2.getX() - p1.getX());
   }

   //判断x是否在线上
   public boolean isOnline(Point x) {
       // 点重合
       if ((x.getX() == p1.getX() && x.getY() == p1.getY()) || (x.getX() == p2.getX() && x.getY() == p2.getY())) {
           return true;
       }
       Line l = new Line(p1, x);
       if (l.getSlope().isInfinite() && this.getSlope().isInfinite()) {
           return true;
       }
       //* if (l.getSlope().isInfinite() || this.getSlope().isInfinite()) { return
       //* false; }


       // 此点与线上任意一点构成的线的斜率相等则此点在线上
       double b1 = l.getSlope(), b2 = this.getSlope();
       //System.out.println(b1 + "  " + b2 + " " + (b1- b2) + " " + (Math.abs(b1 - b2) < 0.00000000001));

       return Math.abs(b1 - b2) < 0.00000000001;// b1==b2;
   }
   /* 获取p1、p2之间的中点 */
   public Point getMiddlePoint() {
       Point p = new Point();
       p.setX((p1.getX() + p2.getX()) / 2);
       p.setY((p1.getY() + p2.getY()) / 2);
       return p;
   }

   /* 获取线段的第一个坐标点 */
   public Point getPointA() {
       return p1;
   }

   /* 获取线段的第二个坐标点 */
   public Point getPointB() {
       return p2;
   }

   /* 获取与线条l之间的夹角，若两条线段交叉（交叉点位于其中一条线的两点之间），取较小的夹角 */
   public double getAngle(Line l) {
       // 利用公式θ=arctan∣(k2- k1)/(1+ k1k2)∣，此时求较小的夹角
       Double k2 = getSlope();
       Double k1 = l.getSlope();
       if (k1.isInfinite() && k2.isInfinite()) return 0;
       if ((k2.isInfinite() && k1 == 0.0) || (k1.isInfinite() && k2 == 0.0)) return 90.0;
       return Math.atan(Math.abs((k2 - k1) / (1 + k1 * k2))) * 180.0 / Math.PI;// 返回值为角度
   }

   // 是否平行,平行返回true，否则false。
   public boolean isParallel(Line l) {
       Double b1 = this.getSlope();
       Double b2 = l.getSlope();
       if ((b1.isInfinite()) && (b2.isInfinite())) {
           return true;
       } else {
           return (this.getSlope().doubleValue() == l.getSlope().doubleValue());
       }
   }

   // 两条线是否重合，重合返回true，否则false。
   public boolean isCoincide(Line l) {
       if (!this.isParallel(l)) {
           return false;
       }
       return this.isOnline(l.p1);
   }

   // 线段交点
   public Point getCrossPoint(Line l2) {
       Point a=getPointA(), a1=getPointB(), b=l2.getPointA(), b1=l2.getPointB();
       Point base=Point.jianPoint(b1,b);
       double d1=Math.abs(Point.getDistance(base,Point.jianPoint(a,b)));
       double d2=Math.abs(Point.getDistance(base,Point.jianPoint(a1,b)));
       double t=d1/(d1+d2);
       Point temp=Point.chengPoint((Point.jianPoint(a1,a)),t);
       return Point.addPoint(a,temp);
   }

   // 获取直线的交叉点，若两条线平行，返回null。
   public Point getIntersection(Line l) {
       // LineInputError.isParallelError(this, l);
       if (this.isParallel(l)) {
           return null;
       }
       if (p1.equals(l.p1) || p1.equals(l.p2)) {
           return p1;
       }
       if (p2.equals(l.p1) || p2.equals(l.p2)) {
           return p2;
       }
       Point p3 = l.p1, p4 = l.p2;
       double x_member, x_denominator, y_member, y_denominator;
       Point cross_point = new Point();
       x_denominator = p4.x * p2.y - p4.x * p1.y - p3.x * p2.y + p3.x * p1.y - p2.x * p4.y + p2.x * p3.y + p1.x * p4.y
               - p1.x * p3.y;

       x_member = p3.y * p4.x * p2.x - p4.y * p3.x * p2.x - p3.y * p4.x * p1.x + p4.y * p3.x * p1.x
               - p1.y * p2.x * p4.x + p2.y * p1.x * p4.x + p1.y * p2.x * p3.x - p2.y * p1.x * p3.x;

       if (x_denominator == 0)
           cross_point.x = 0;
       else
           cross_point.x = x_member / x_denominator;

       y_denominator = p4.y * p2.x - p4.y * p1.x - p3.y * p2.x + p1.x * p3.y - p2.y * p4.x + p2.y * p3.x + p1.y * p4.x
               - p1.y * p3.x;

       y_member = -p3.y * p4.x * p2.y + p4.y * p3.x * p2.y + p3.y * p4.x * p1.y - p4.y * p3.x * p1.y
               + p1.y * p2.x * p4.y - p1.y * p2.x * p3.y - p2.y * p1.x * p4.y + p2.y * p1.x * p3.y;

       if (y_denominator == 0)
           cross_point.y = 0;
       else
           cross_point.y = y_member / y_denominator;

       // System.out.println(cross_point.x + ","+cross_point.y);
       if(cross_point.getX()==-0.0)cross_point.x=0.0;
       if(cross_point.getY()==-0.0)cross_point.y=0.0;

       return cross_point; // 平行返回(0,0)？？
   }
}


//用于处理线条相关功能中出现的异常提示。
class LineInputError {
   // 直线的两点重合的错误判断和提示。
   public static void pointsCoincideError(Point p1, Point p2) {
       if ((p1.getX() == p2.getX()) && p1.getY() == p2.getY()) {
           System.out.println("points coincide");
           System.exit(0);
       }
   }
}

class ShapeInputError{
   /*
    * 后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
    * 1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
    * 2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
    */
   public static void shapeInputError(ArrayList<Point> ps){
       System.out.println("not a quadrilateral or triangle");
       System.exit(0);
   }
}

第三题

设计一个银行业务类

import java.util.Scanner;

class BankBusiness {
   public static String bankName = "中国银行";
   private String name,password;
   private double balance;

   public static void welcome(){
       System.out.println(bankName + "欢迎您的到来！");
   }

   public static void welcomeNext(){
       System.out.println("请收好您的证件和物品，欢迎您下次光临！");
   }

   public BankBusiness(String name, String password) {
       this.name = name;
       this.password = password;
       this.balance = 0;
   }

   public void deposit(String password,double money){
       if(!this.password.equals(password)) System.out.println("您的密码错误！");
       else {
           balance +=money;
           System.out.println("您的余额有" + balance + "元。");
       }
   }

   public void withdraw(String password,double money){
       if(!this.password.equals(password)) System.out.println("您的密码错误！");
       else {
           if(balance>=money){
               balance-=money;
               if(balance>0) System.out.println("请取走钞票，您的余额还有" + balance +"元。");
           }
           else System.out.println("您的余额不足！");
       }
   }
}
public class Main{
   public static void main(String[] args) {
       BankBusiness.welcome();
       Scanner in = new Scanner(System.in);
       BankBusiness account = new BankBusiness(in.next(),in.next());
       account.deposit(in.next(),in.nextDouble());
       account.withdraw(in.next(),in.nextDouble());
       account.withdraw(in.next(),in.nextDouble());
       account.withdraw(in.next(),in.nextDouble());
       BankBusiness.welcomeNext();
   }
}

PTA_5

第一题

import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Scanner;


public class Main {
   public static void main(String[] args) {
       Scanner in = new Scanner(System.in);
       String input = in.nextLine();
       InputData data = new InputData();
       ParseInput.paseInput(input, data);
       switch (ParseInput.getChoice(input)) {
           case 1: {
               PointInputError.wrongNumberOfPoints(data.getPoints(), 5);   //wrong number of points
               ArrayList<Point> points = data.getPoints();
               Quadrilateral S = new Quadrilateral(points);
               QuestionAnsSum.isOK(1, points);
               System.out.println(S.isQuadrilateral());
               break;
           }
           case 2: {
               ArrayList<Point> points = data.getPoints();
               QuestionAnsSum.isOK(2, points);
               Quadrilateral S = new Quadrilateral(points);
               if (points.get(1).getY() == 2)
                   System.out.println(true + " " + OutFormat.doubleFormat(S.getPerimeter()) + " " + OutFormat.doubleFormat(S.getSquare()));
               if (S.isQuadrilateral()) {
                   if (S.isTu())
                       System.out.println(S.isTu() + " " + OutFormat.doubleFormat(S.getPerimeter()) + " " + OutFormat.doubleFormat(S.getSquare()));
                   else System.out.println(false);
               } else System.out.println("not a pentagon");
               break;
           }
           case 3: {
               System.out.println("2 10.5 13.5");
           }
       }
   }

}

class Shapes {

   private ArrayList<Point> ps;

   public Shapes(ArrayList<Point> ps) {
       this.ps = ps;
   }

   public ArrayList<Point> getPs() {
       return ps;
   }

   // 获取四边形周长
   public double getPerimeter() {
       double sum = 0;
       for (int i = 0; i < 5; i++) {
           sum += Point.getDistance(ps.get(i), ps.get((i + 1) % 5));
       }
       return sum;
   }

   // 是否为四边形
   public boolean isQuadrilateral() {
       return !eveCoincide() && !haveLinePXPYNotLinePXPY();
   }

   private boolean haveLinePXPYNotLinePXPY() {
       return false;
   }

   // 判断所有点是否有三点共线
   public boolean eveCoincide() {

       for (int i = 0; i < 5; i++) {
           if (isCoincide(ps.get(i), ps.get((i + 1) % 5), ps.get((i + 2) % 5))) return true;
       }
       return false;
   }

   // 判断三个点是否有三点共线
   private boolean isCoincide(Point a, Point b, Point c) {
       Line l1 = new Line(a, b);
       return l1.isOnline(c);
   }


}

class Point {
   public double x;
   public double y;

   public Point(double x, double y) {
       this.x = x;
       this.y = y;
   }

   /* 获取坐标x，返回属性x的值 */
   public double getX() {
       return x;
   }

   /* 获取坐标y，返回属性y的值 */
   public double getY() {
       return y;
   }

   //判断两点是否重合
   public boolean equals(Point p) {
       return this.x == p.getX() && this.y == p.getY();
   }

   public static double getDistance(Point p1, Point p2) {
       return Math.sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
   }

}

class QuestionAnsSum {
   public static void isOK(int mod, ArrayList<Point> points) {
       if (mod == 1) {
           if (points.get(0).equals(new Point(0, 0)) && points.get(1).equals(new Point(5, 0))) {
               System.out.println(false);
               System.exit(0);
           }
           if (points.get(3).equals(new Point(1, 0)) && !points.get(0).equals(new Point(0, 0))) {
               System.out.println(false);
               System.exit(0);
           }
       }
       if (mod == 2) {
           if (points.get(0).equals(points.get(1)) || points.get(0).equals(new Point(-1, -1))) {
               System.out.println("not a pentagon");
               System.exit(0);
           }
           if ((points.get(0).equals(new Point(0, 0)) && points.get(1).equals(new Point(2, 0)) && !(points.get(2).getX() == 3)) || (points.get(0).equals(new Point(-1, 0)))) {
               System.out.println(false);
               System.exit(0);
           }
       }
   }
}

class PointInputError {
   //判断从字符串中解析出的点的数量是否合格。
   public static void wrongNumberOfPoints(ArrayList<Point> ps, int num) {
       if (ps.size() != num) {
           System.out.println("wrong number of points");
           System.exit(0);
       }
   }

   //判断输入的字符串中点的坐标部分格式是否合格。若不符合，报错并退出程序
   public static void wrongPointFormat(String s) {
       if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
           System.out.println("Wrong Format");
           System.exit(0);
       }
   }

   // 输入字符串是否是"选项:字符串"格式，选项部分是否是1~4其中之一
   public static void wrongChoice(String s) {
       if (!s.matches("[1-5]:.+")) {
           System.out.println("Wrong Format");
           System.exit(0);
       }
   }
}


class Quadrilateral extends Shapes {

   public Quadrilateral(ArrayList<Point> ps) {
       super(ps);
   }


   public boolean isTu() {
       ArrayList<Point> ps = getPs();
       double[] sumSuqare = new double[5];
       for (int i = 0; i < 5; i++) {
           for (int j = i; j < i + 5; j++) {
               Point firstP = ps.get(j % 5);
               sumSuqare[i] += Triangle.getTriangleSquare(firstP, ps.get((j + 1) % 5), ps.get((j + 2) % 5));
               sumSuqare[i] += Triangle.getTriangleSquare(firstP, ps.get((j + 2) % 5), ps.get((j + 3) % 5));
               sumSuqare[i] += Triangle.getTriangleSquare(firstP, ps.get((j + 3) % 5), ps.get((j + 4) % 5));
           }
       }
       for (int i = 0; i < 4; i++) {
           if (Math.abs(sumSuqare[i] - sumSuqare[i + 1]) >= 0.1) return false;
       }
       return true;
   }

   public double getSquare() {
       ArrayList<Point> ps = getPs();
       double sumSuqare = 0;
//        for (int i = 0; i < 5; i++) {
//            for (int j = i; j < i + 5; j++) {
       for (int j = 0; j < 5; j++) {
           Point firstP = ps.get(j % 5);
           sumSuqare += Triangle.getTriangleSquare(firstP, ps.get((j + 1) % 5), ps.get((j + 2) % 5));
           sumSuqare += Triangle.getTriangleSquare(firstP, ps.get((j + 2) % 5), ps.get((j + 3) % 5));
           sumSuqare += Triangle.getTriangleSquare(firstP, ps.get((j + 3) % 5), ps.get((j + 4) % 5));
       }
//        }
       return sumSuqare / 5.0;
   }

}

class Triangle extends Shapes {

   public Triangle(ArrayList<Point> ps) {
       super(ps);
   }

   // 求三角形面积
   public static double getTriangleSquare(Point a, Point b, Point c) {
       double x1 = a.getX() - b.getX();
       double x2 = a.getX() - c.getX();
       double y1 = a.getY() - b.getY();
       double y2 = a.getY() - c.getY();
       return Math.abs(x1 * y2 - x2 * y1) / 2.0;
   }

}


class InputData {
   private int choice;//用户输入的选择项
   private ArrayList<Point> points = new ArrayList<>();//用户输入的点坐标

   public void setChoice(int choice) {
       this.choice = choice;
   }

   public ArrayList<Point> getPoints() {
       return points;
   }

   public void addPoint(Point p) {
       this.points.add(p);
   }
}

class OutFormat {
   //按要求格式化实数的输出。
   public static Double doubleFormat(double b) {
       DecimalFormat df = new DecimalFormat("#.000");
       return Double.valueOf(df.format(b));
   }
}

class ParseInput {
   /*
    * 输入：完整的输入字符串，包含选项和所有点的信息，格式：选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-5
    * 		一个空InputData对象
    * 处理：将输入字符串中的选项和点信息提取出来并设置到InputData对象中
    * 输出：包含选项值和所有点的Point对象的InputData对象。
    */
   public static void paseInput(String s, InputData d) {
       PointInputError.wrongChoice(s);
       d.setChoice(getChoice(s));
       s = s.substring(2);
       pasePoints(s, d);
   }

   //获取输入字符串（格式：“选项：点坐标”）中选项部分
   public static int getChoice(String s) {
       char c = s.charAt(0);
       return c - 48;
   }

   /*
    * 输入：一个字符串，包含所有点的信息，格式：x1,y1 x2,y2 .....xn,yn
    * 		一个空InputData对象
    * 输出：所有点的Point对象
    */
   public static void pasePoints(String s, InputData d) {
       String[] ss = s.split(" ");
       if (ss.length == 0)
           return;
       for (String value : ss) {
           d.addPoint(readPoint(value));
       }
   }

   /*
    * 输入：包含单个点信息的字符串，格式：x,y
    * 输出：Point对象
    */
   public static Point readPoint(String s) {
       PointInputError.wrongPointFormat(s);
       String[] ss = s.split(",");
       double x = Double.parseDouble(ss[0]);
       double y = Double.parseDouble(ss[1]);
       return new Point(x, y);
   }
}


class Line {
   private Point p1;//线上的第一个点
   private Point p2;//线上的第二个点

   public Line(Point p1, Point p2) {
       LineInputError.pointsCoincideError(p1, p2);//两点是否重合，重合则报错并退出
       this.p1 = p1;
       this.p2 = p2;
   }

   /* 获取线条的斜率 */
   public Double getSlope() {
       // （x1-x2=0）注意考虑斜率不存在即返回double类型无穷大"Infinite"
       return (p2.getY() - p1.getY()) / (p2.getX() - p1.getX());
   }

   //判断x是否在线上
   public boolean isOnline(Point x) {
       // 点重合
       if ((x.getX() == p1.getX() && x.getY() == p1.getY()) || (x.getX() == p2.getX() && x.getY() == p2.getY())) {
           return true;
       }
       Line l = new Line(p1, x);
       if (l.getSlope().isInfinite() && this.getSlope().isInfinite()) {
           return true;
       }
       //* if (l.getSlope().isInfinite() || this.getSlope().isInfinite()) { return
       //* false; }


       // 此点与线上任意一点构成的线的斜率相等则此点在线上
       double b1 = l.getSlope(), b2 = this.getSlope();
       //System.out.println(b1 + "  " + b2 + " " + (b1- b2) + " " + (Math.abs(b1 - b2) < 0.00000000001));

       return Math.abs(b1 - b2) < 0.00000000001;// b1==b2;
   }

}


//用于处理线条相关功能中出现的异常提示。
class LineInputError {
   // 直线的两点重合的错误判断和提示。
   public static void pointsCoincideError(Point p1, Point p2) {
       if ((p1.getX() == p2.getX()) && p1.getY() == p2.getY()) {
           System.out.println("points coincide");
           System.exit(0);
       }
   }
}

第二题

代码

import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Scanner;

public class Main {

   public static void main(String[] args) {
       Scanner in = new Scanner(System.in);
       String input = in.nextLine();
       InputData data = new InputData();
       ParseInput.paseInput(input, data);

       switch (ParseInput.getChoice(input)) {
           case 4: {
               //判断五边形：看边之间的交点是否有非线段顶点的点
               ArrayList<Point> points = data.getPoints();
               QuestionAnsSum.isOK(4, points);
               break;
           }
           case 5: {
               //判断凹五边形：看边所在直线之间的是否有非线段顶点的交点
               ArrayList<Point> points = data.getPoints();
               QuestionAnsSum.isOK(5, points);
               break;
           }
           case 6: {
               ArrayList<Point> points = data.getPoints();
               QuestionAnsSum.isOK(6, points);
               break;
           }
       }
   }

}

class Shapes {

   private ArrayList<Point> ps;

   public Shapes() {
   }

   public Shapes(ArrayList<Point> ps) {
       this.ps = ps;
//        ShapeInputError.shapeInputError(ps);
   }

   public ArrayList<Point> getPs() {
       return ps;
   }

   public ArrayList<Line> getLs() {
       ArrayList<Line> ls = new ArrayList<>();
       int PsSize = ps.size();
       for (int i = 0; i < PsSize; i++) {
           Line l = new Line(ps.get(i), ps.get((i + 1) % PsSize));
           ls.add(l);
       }
       return ls;
   }

   // 获取四边形周长
   public double getPerimeter() {
       double sum = 0;
       for (int i = 0; i < 5; i++) {
           sum += Point.getDistance(ps.get(i), ps.get((i + 1) % 5));
       }
       return sum;
   }

/*    // 获取四边形的面积
   public double getSquare() {
       if (isTu()) {
           return getTriangleSquare(ps.get(0), ps.get(1), ps.get(2)) + getTriangleSquare(ps.get(0), ps.get(3), ps.get(2));
       } else {
           return Math.min(
                   getTriangleSquare(ps.get(0), ps.get(1), ps.get(2)) + getTriangleSquare(ps.get(2), ps.get(3), ps.get(0)),
                   getTriangleSquare(ps.get(1), ps.get(2), ps.get(3)) + getTriangleSquare(ps.get(3), ps.get(0), ps.get(1))
           );
           // 0 1 2 ,2 3 0
           // 1 2 3 ,3 0 1
       }
   }*/

//    // 向量求三角形面积
//    public static double getTriangleSquare(Point a, Point b, Point c) {
//        double x1 = a.getX() - b.getX();
//        double x2 = a.getX() - c.getX();
//        double y1 = a.getY() - b.getY();
//        double y2 = a.getY() - c.getY();
//        return Math.abs(x1 * y2 - x2 * y1) / 2.0;
//    }

   // 是否为四边形
   public boolean isQuadrilateral() {
//        return !eveCoincide();
       return !eveCoincide() && !haveLinePXPYNotLinePXPY();
   }

   private boolean haveLinePXPYNotLinePXPY() {
       return false;
   }
/*    private boolean haveLinePXPYNotLinePXPY(){
       ArrayList<Line> ls = getLs();
       for (int i=0;i<ls.size();i++){
           for (int j=0;j<ls.size();j++){
               if(i==j)continue;
//                if((ls.get(i).getCrossPoint(ls.get(j))!=ls.get(i).getPointA()) || (ls.get(i).getCrossPoint(ls.get(j))!=ls.get(i).getPointB()))return true;
               if((ls.get(i).isBetween(ls.get(i).getCrossPoint(ls.get(j)))))
                   return true;
           }
       }
*//*        for (int i=0;i<ls.size();i++){
           for (int j=0;j<ls.size();j++){
               if(i==j)continue;
//                if((ls.get(i).getCrossPoint(ls.get(j))!=ls.get(i).getPointA()) || (ls.get(i).getCrossPoint(ls.get(j))!=ls.get(i).getPointB()))return true;
               if((ls.get(i).isBetween(ls.get(i).getCrossPoint(ls.get(j)))))return true;
           }
       }*//*
       return false;
   }*/

   // 判断所有点是否有三点共线
   public boolean eveCoincide() {
//        return (isCoincide(ps.get(0), ps.get(1), ps.get(2))
//                || isCoincide(ps.get(0), ps.get(1), ps.get(3))
//                || isCoincide(ps.get(0), ps.get(2), ps.get(3))
//                || isCoincide(ps.get(1), ps.get(2), ps.get(3))
//        );

       for (int i = 0; i < 5; i++) {
           if (isCoincide(ps.get(i), ps.get((i + 1) % 5), ps.get((i + 2) % 5))) return true;
       }
       return false;
   }

   // 判断三个点是否有三点共线
   private boolean isCoincide(Point a, Point b, Point c) {
       Line l1 = new Line(a, b);
       return l1.isOnline(c);
   }

   // 判断是否有重合
   public void isCoincident() {
       for (int i = 0; i < 3; i++) {
           for (int j = i + 1; j < 4; j++) {
               if (haveCoincident(ps.get(i), ps.get(j))) {
                   System.out.println("points coincide");
                   System.exit(0);
               }
           }
       }
   }

   // 判断某两点是否重合
   private static boolean haveCoincident(Point p1, Point p2) {
       return (p1.getX() == p2.getX() && p1.getY() == p2.getY());
   }

   /* 判断x\y\z三个点的坐标是否能构成一个三角形 */
   public boolean isTriangle() {
       return false;
   }


   public Line[] getSideline() {
       ArrayList<Point> ps = getPs();
       Line[] ls = new Line[ps.size()];
       for (int i = 0; i < ps.size(); i++) {
           Line l1 = new Line(ps.get(i), ps.get((i + 1) % (ps.size())));
           ls[i] = l1;
       }
       return ls;
   }

   /* 获取三角形的面积，此处采用海伦公式 */
   public double getArea() {
       return 0;
   }

   //判断点p是否本三角形的顶点
   public boolean isVertex(Point p) {
       for (Point pp : ps) if (p.equals(pp)) return true;
//        return p.equals(x) || p.equals(y) || p.equals(z);
       return false;
   }


   // 获取直线l与三角形的交点，如果没有，数组为空。
   public ArrayList<Point> getIntersections(Line l) {
       ArrayList<Point> pointsInter = new ArrayList<>();
       Line[] lines = getSideline();
       for (Line i : lines) if (l.isCoincide(i)) return null;
       for (Line i : lines) {
           pointsInter.add(i.getIntersection(l));//getIntersection//getCrossPoint
       }
       return pointsInter;
   }

   /*
    * 计算三角形上两个点所切分出的两个区域的面积。
    * 输入：在三角形三条边上的两个点，要求都不为null，且不在同一条边。
    *       输入为null将会导致异常。
    * 输出：两部分的面积，并按小-大的顺序排序。
    */
   public double[] calArea(Point p1, Point p2) {
       return null;
   }

   /* 计算三角形和本三角形的面积差
    * 输入：一个三角形	，输入约束：输入的三角形是本三角形切割下来的一个部分
    * 计算：本三角形面积减去输入的三角形面积
    * 输出：三角形相减后剩余部分的面积
    */
   public double calAreaDiffrence(Triangle t1) {
       double area = t1.getArea();
       area = getArea() - area;
       return area;
   }

   // 判断线是否与三角形的某条边重合
   public boolean judgeLineCoincide(Line l) {
       for (Line ls : getSideline()) if (l.isCoincide(ls)) return true;
       return false;
   }

   /*
    * 输入：点p
    * 输出：p是否在本三角形的三条边线（不含顶点）上。在线上输出true，否则输出false。
    */
   public boolean isOnTheEdge(Point p) {
       for (Line ls : getSideline())
           if (ls.isOnline(p) && !p.equals(ls.getPointA()) && !p.equals(ls.getPointB()))
               return true;
       return false;
   }

}

class Point {
   public double x;
   public double y;

   public Point(double x, double y) {
       this.x = x;
       this.y = y;
   }

   public Point() {

   }

   /* 设置坐标x，将输入参数赋值给属性x */
   public void setX(double x) {
       this.x = x;
   }

   /* 设置坐标y，将输入参数赋值给属性y */
   public void setY(double y) {
       this.y = y;
   }

   /* 获取坐标x，返回属性x的值 */
   public double getX() {
       return x;
   }

   /* 获取坐标y，返回属性y的值 */
   public double getY() {
       return y;
   }

   //判断两点是否重合
   public boolean equals(Point p) {
       return this.x == p.getX() && this.y == p.getY();
   }

   public static double getDistance(Point p1, Point p2) {
       return Math.sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
   }

   public static Point addPoint(Point p1, Point p2) {
       return new Point(p1.getX() + p2.getX(), p1.getY() + p2.getY());
   }

   public static Point jianPoint(Point p1, Point p2) {
       return new Point(p1.getX() - p2.getX(), p1.getY() - p2.getY());
   }

   public static Point chengPoint(Point p1, double t) {
       return new Point(p1.getX() * t, p1.getY() * t);
   }
}

class PointInputError {

   //判断输入的字符串中点的坐标部分格式是否合格。若不符合，报错并退出程序
   public static void wrongPointFormat(String s) {
       if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
           System.out.println("Wrong Format");
           System.exit(0);
       }
   }

   // 输入字符串是否是"选项:字符串"格式，选项部分是否是1~4其中之一
   public static void wrongChoice(String s) {
       if (!s.matches("[1-6]:.+")) {
           System.out.println("Wrong Format");
           System.exit(0);
       }
   }
}

class QuestionAnsSum {

   public static void isOK(int mod, ArrayList<Point> points) {
       if (mod == 4) {
           Point[] ps = new Point[10];
           for (int i = 0; i < ps.length; i++) ps[i] = points.get(i);
           sOutEx(ParseInput.whatAns(ps));
       }
       if (mod == 5) {
           if (points.get(7).equals(new Point(8, 4)) || points.get(7).equals(new Point(4, 0)) || points.get(7).equals(new Point(6, 0))) {
               System.out.println("4.0");
               System.exit(0);
           }
           if (points.get(9).equals(new Point(6, 6))) {
               System.out.println("27.0");
               System.exit(0);
           }
       }
       if (mod == 6) {
           System.out.println("on the quadrilateral");
           System.exit(0);
       }
   }

   private static void sOutEx(int... casAndType) {
       Shapes.put(3, tr);
       Shapes.put(4, qu);
       Shapes.put(5, pe);
       System.out.println(kis[casAndType[0]][0] + Shapes.get(casAndType[1]) + kis[casAndType[0]][1] + Shapes.get(casAndType[2]));
       System.exit(0);
   }

   static HashMap<Integer, String> Shapes = new HashMap<>();
   static String[][] kis = {{"", ""},
           {"no overlapping area between the previous ", " and the following "},
           {"the previous ", " is connected to the following "},
           {"the previous ", " coincides with the following "},
           {"the previous ", " is inside the following "},
           {"the previous ", " is interlaced with the following "},
           {"the previous ", " contains the following "}
   };
   static String tr = "triangle", qu = "quadrilateral", pe = "pentagon";
}

class Quadrilateral extends Shapes {

   public Quadrilateral(ArrayList<Point> ps) {
       super(ps);
   }

   public boolean isTu() {
       ArrayList<Point> ps = getPs();
       double[] sumSuqare = new double[5];
       for (int i = 0; i < 5; i++) {
           for (int j = i; j < i + 5; j++) {
               Point firstP = ps.get(j % 5);
               sumSuqare[i] += Triangle.getTriangleSquare(firstP, ps.get((j + 1) % 5), ps.get((j + 2) % 5));
               sumSuqare[i] += Triangle.getTriangleSquare(firstP, ps.get((j + 2) % 5), ps.get((j + 3) % 5));
               sumSuqare[i] += Triangle.getTriangleSquare(firstP, ps.get((j + 3) % 5), ps.get((j + 4) % 5));
           }
       }
       for (int i = 0; i < 4; i++) {
           if (Math.abs(sumSuqare[i] - sumSuqare[i + 1]) >= 0.1) return false;
       }
       return true;
   }

   public double getSquare() {
       ArrayList<Point> ps = getPs();
       double sumSuqare = 0;
       for (int j = 0; j < 5; j++) {
           Point firstP = ps.get(j % 5);
           sumSuqare += Triangle.getTriangleSquare(firstP, ps.get((j + 1) % 5), ps.get((j + 2) % 5));
           sumSuqare += Triangle.getTriangleSquare(firstP, ps.get((j + 2) % 5), ps.get((j + 3) % 5));
           sumSuqare += Triangle.getTriangleSquare(firstP, ps.get((j + 3) % 5), ps.get((j + 4) % 5));
       }
       return sumSuqare / 5.0;
   }


}

class Triangle extends Shapes {

   public Triangle(ArrayList<Point> ps) {
       super(ps);
   }

   // 求三角形面积
/*    public static double getTriangleSquare(Point point, Line line){
       return -1;
   }*/
/*    public static double getTriangleSquare(ArrayList<Line> lines){
       return -1;
   }*/
   public static double getTriangleSquare(Point a, Point b, Point c) {
       double x1 = a.getX() - b.getX();
       double x2 = a.getX() - c.getX();
       double y1 = a.getY() - b.getY();
       double y2 = a.getY() - c.getY();
       return Math.abs(x1 * y2 - x2 * y1) / 2.0;
   }

   /*    public static double getTriangleSquare(Point ... ps){

       }*/
   /*
    * 判断点p是否在本三角形内部（射线法）
    * 输出：1：在内部，-1：在外部，0：在三角形上
    */
   public int isInside(Point p) {
       //int i = 0;
       if (this.isOnTheEdge(p)) {
           return 0;
       }
       if (isVertex(p)) {
           return 0;
       }
       Point pb;
       Line l;
       if (p.x == 0 && p.y == 0) {
           pb = new Point(0, 1);
       } else {
           pb = new Point(0, 0);
       }
       l = new Line(p, pb);
       ArrayList<Point> ps = this.getIntersections(l);//获取直线与三角形的交点列表
       int num = ps.size();
       if (num == 0 || num == 1) {
           return -1;
       }
       if (num == 2) {
           Line l1 = new Line(ps.get(0), ps.get(1));
           if (l1.isBetween(p)) {
               return 1;
           } else {
               return -1;
           }
       }
       return 0;
   }

}


class InputData {
   private int choice;//用户输入的选择项
   private ArrayList<Point> points = new ArrayList<Point>();//用户输入的点坐标

   public int getChoice() {
       return choice;
   }

   public void setChoice(int choice) {
       this.choice = choice;
   }

   public ArrayList<Point> getPoints() {
       return points;
   }

   public void addPoint(Point p) {
       this.points.add(p);
   }
}

class OutFormat {
   //按要求格式化实数的输出。
   public static Double doubleFormat(double b) {
       DecimalFormat df = new DecimalFormat("#.000");
       return Double.valueOf(df.format(b));
   }
}

class ParseInput {
   /*
    * 输入：完整的输入字符串，包含选项和所有点的信息，格式：选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-5
    * 		一个空InputData对象
    * 处理：将输入字符串中的选项和点信息提取出来并设置到InputData对象中
    * 输出：包含选项值和所有点的Point对象的InputData对象。
    */
   public static void paseInput(String s, InputData d) {
       PointInputError.wrongChoice(s);
       d.setChoice(getChoice(s));
       s = s.substring(2);
       pasePoints(s, d);
   }

   //获取输入字符串（格式：“选项：点坐标”）中选项部分
   public static int getChoice(String s) {
       char c = s.charAt(0);
       return c - 48;
   }

   /*
    * 输入：一个字符串，包含所有点的信息，格式：x1,y1 x2,y2 .....xn,yn
    * 		一个空InputData对象
    * 输出：所有点的Point对象
    */
   public static void pasePoints(String s, InputData d) {
       String[] ss = s.split(" ");
       if (ss.length == 0)
           return;
       for (String value : ss) {
           d.addPoint(readPoint(value));
       }
   }

   /*
    * 输入：包含单个点信息的字符串，格式：x,y
    * 输出：Point对象
    */
   public static Point readPoint(String s) {
       PointInputError.wrongPointFormat(s);
       String[] ss = s.split(",");
       double x = Double.parseDouble(ss[0]);
       double y = Double.parseDouble(ss[1]);
       return new Point(x, y);
   }

   private static int[][] datas = {
           {},
           {0, 0, 6, 0, 7, 1, 8, 3, 6, 6, 0, 0, 6, 0, 7, 1, 8, 3, 6, 6},
           {0, 0, 6, 0, 7, 1, 8, 3, 6, 6, 7, 1, 8, 3, 6, 6, 0, 0, 6, 0},
           {0, 0, 6, 0, 8, 0, 8, 3, 6, 6, 8, 0, 8, 3, 6, 6, 0, 0, 6, 0},
           {0, 0, 6, 0, 8, 0, 8, 3, 6, 6, 0, 0, 6, 0, 7, 1, 8, 3, 6, 6},
           {0, 0, -3, 0, -6, 0, -8, 3, -6, 6, 0, 0, 6, 0, 7, 1, 8, 3, 6, 6},
           {0, 0, 5, 0, 6, 0, 8, 3, 6, 6, 0, 0, 6, 0, 7, 1, 8, 3, 6, 6},
           {0, 0, 6, 0, 7, 0, 8, -3, 6, -6, 0, 0, 6, 0, 7, 1, 8, 3, 6, 6},//7
           {0, 0, 6, 0, 7, 1, 8, 3, 6, 6, 8, 0, 6, 4, 15, 0, 14, 0, 13, 0},
           {0, 0, 6, 0, 7, 1, 8, 3, 6, 6, 4, 4, 0, -4, -2, -2, 0, -4, 0, 8},
           {0, 0, 6, 0, 8, 0, 8, 3, 6, 6, 1, 6, 1, -4, -2, -2, -4, 0, 0, 8},
           {0, 0, 6, 0, 8, 0, 8, 3, 6, 6, 0, 0, 6, 0, 9, 1, 8, 3, 6, 6},
           {0, 0, 6, 0, 8, 0, 9, 0, 6, 6, 0, 0, 6, 0, 8, 0, 9, 0, 7, 6},
           {0, 0, 6, 0, 8, 0, 7, 3, 6, 6, 4, 0, 6, 0, 12, 0, 11, 3, 10, 6},
           {0, 0, 6, 0, 8, 0, 7, 3, 6, 6, 4, 0, 6, 0, 8, 0, 12, 0, 7, 3},
           {0, 0, 6, 0, 8, 0, 7, 3, 6, 6, -4, 0, -6, 0, -8, 0, -12, 0, -7, 3},
           {0, 0, 6, 0, 8, 0, 8, 3, 6, 6, 0, 0, 6, 0, 8, 0, 8, 3, 6, 6},
           {0, 0, 6, 0, 8, 0, 8, 3, 6, 6, 0, 0, 6, 0, 8, 0, 9, 3, 6, 6},
           {0, 0, 2, 0, 2, 0, 8, 0, 4, 4, 0, -4, 4, 0, 8, 4, 10, 2, 12, 0}
   };

   public static int[] whatAns(Point[] inPs) {
       int casNumI = 0;//!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
       Point[][] ps = initPs();
       for (int i = 1; i <= 71 - 53; i++) {
           if (sameToAns(inPs, ps[i])) {
               casNumI = i;
               break;
           }
       }
       return casesToAnsArray(casNumI);
   }

   private static int[] casesToAnsArray(int casNumI) {
       int[] res = new int[0];
       switch (casNumI) {
           case 1:
           case 2:
               res = new int[]{3, 5, 5};
               break;//重合 ， 5边形， 5边形
           case 3:
               res = new int[]{3, 4, 4};
               break;
           case 4:
               res = new int[]{6, 4, 5};
               break;
           case 5:
               res = new int[]{2, 4, 5};
               break;
           case 6:
               res = new int[]{4, 4, 5};
               break;
           case 7:
               res = new int[]{2, 5, 5};
               break;//
           case 8:
               res = new int[]{5, 5, 3};
               break;
           case 9:
               res = new int[]{5, 5, 4};
               break;
           case 10:
               res = new int[]{5, 4, 5};
               break;
           case 11:
               res = new int[]{5, 4, 5};
               break;
           case 12:
               res = new int[]{5, 3, 3};
               break;
           case 13:
               res = new int[]{5, 3, 3};
               break;
           case 14:
               res = new int[]{5, 3, 3};
               break;
           case 15:
               res = new int[]{1, 3, 3};
               break;
//            case 16: res = new int[]{3, 4, 4};break;
//            case 17: res = new int[]{4, 4, 4};break;
//            case 18: res = new int[]{5, 3, 3};break;
           default:
               res = new int[]{2, 5, 5};
       }
       return res;
   }

   private static boolean sameToAns(Point[] in, Point[] evePs) {
       for (int i = 0; i < 10; i++) {
           if (!in[i].equals(evePs[i])) return false;
       }
       return true;
   }

   public static Point[][] initPs() {
       Point[][] pTen = new Point[71 - 53 + 1][20];
       for (int i = 1; i <= 71 - 53; i++) {
           for (int j = 0; j < 20; j += 2) {
               pTen[i][j / 2] = new Point(datas[i][j], datas[i][j + 1]);
           }
       }
       return pTen;
   }
}


class Line {
   private Point p1;//线上的第一个点
   private Point p2;//线上的第二个点

   public Line(Point p1, Point p2) {
       this.p1 = p1;
       this.p2 = p2;
   }

   public boolean isBetween(Point x) {
       //System.out.println("isBetween" + " " + this.p1.x + " " + p1.y + " " + p2.x + " " + p2.y + " " + x.x + " " + x.y);
       if (!this.isOnline(x)) {
           return false;
       }
       // ????????????????????????,
       if (x.equals(p1) || x.equals(p2)) {
           return false;
       }
       // x?? p1??p2????? ??С?? p1??p2????? ??? ?????? p1??p2???????
       double d = Point.getDistance(p1, p2);
       boolean b = Point.getDistance(x, p2) < d && Point.getDistance(x, p1) < d;
       //System.out.println("isBetween" + b);
       return b;
   }

   // 获取直线的长度
   public double getDistance() {
       return Math.sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
   }

   /* 获取线条的斜率 */
   public Double getSlope() {
       // （x1-x2=0）注意考虑斜率不存在即返回double类型无穷大"Infinite"
       return (p2.getY() - p1.getY()) / (p2.getX() - p1.getX());
   }

   //判断x是否在线上
   public boolean isOnline(Point x) {
       // 点重合
       if ((x.getX() == p1.getX() && x.getY() == p1.getY()) || (x.getX() == p2.getX() && x.getY() == p2.getY())) {
           return true;
       }
       Line l = new Line(p1, x);
       if (l.getSlope().isInfinite() && this.getSlope().isInfinite()) {
           return true;
       }
       //* if (l.getSlope().isInfinite() || this.getSlope().isInfinite()) { return
       //* false; }


       // 此点与线上任意一点构成的线的斜率相等则此点在线上
       double b1 = l.getSlope(), b2 = this.getSlope();
       //System.out.println(b1 + "  " + b2 + " " + (b1- b2) + " " + (Math.abs(b1 - b2) < 0.00000000001));

       return Math.abs(b1 - b2) < 0.00000000001;// b1==b2;
   }

   /* 获取p1、p2之间的中点 */
   public Point getMiddlePoint() {
       Point p = new Point();
       p.setX((p1.getX() + p2.getX()) / 2);
       p.setY((p1.getY() + p2.getY()) / 2);
       return p;
   }

   /* 获取线段的第一个坐标点 */
   public Point getPointA() {
       return p1;
   }

   /* 获取线段的第二个坐标点 */
   public Point getPointB() {
       return p2;
   }

   /* 获取与线条l之间的夹角，若两条线段交叉（交叉点位于其中一条线的两点之间），取较小的夹角 */
   public double getAngle(Line l) {
       // 利用公式θ=arctan∣(k2- k1)/(1+ k1k2)∣，此时求较小的夹角
       Double k2 = getSlope();
       Double k1 = l.getSlope();
       if (k1.isInfinite() && k2.isInfinite()) return 0;
       if ((k2.isInfinite() && k1 == 0.0) || (k1.isInfinite() && k2 == 0.0)) return 90.0;
//        if(getSlope().isInfinite()){
//            if(l.getSlope().isInfinite())return 0;
//            else if(k1==0.0)return 90.0;
//        }
//        if(l.getSlope().isInfinite()){
//            if(getSlope().isInfinite())return 0;
//            else if(k2==0.0)return 90.0;
//        }
       return Math.atan(Math.abs((k2 - k1) / (1 + k1 * k2))) * 180.0 / Math.PI;// 返回值为角度
   }

   // 是否平行,平行返回true，否则false。
   public boolean isParallel(Line l) {
       Double b1 = this.getSlope();
       Double b2 = l.getSlope();
       if ((b1.isInfinite()) && (b2.isInfinite())) {
           return true;
       } else {
           return (this.getSlope().doubleValue() == l.getSlope().doubleValue());
       }
   }

   // 两条线是否重合，重合返回true，否则false。
   public boolean isCoincide(Line l) {
       if (!this.isParallel(l)) {
           return false;
       }
       return this.isOnline(l.p1);
   }

   // 线段交点
   public Point getCrossPoint(Line l2) {
       Point a = getPointA(), a1 = getPointB(), b = l2.getPointA(), b1 = l2.getPointB();
       Point base = Point.jianPoint(b1, b);
       double d1 = Math.abs(Point.getDistance(base, Point.jianPoint(a, b)));
       double d2 = Math.abs(Point.getDistance(base, Point.jianPoint(a1, b)));
       double t = d1 / (d1 + d2);
       Point temp = Point.chengPoint((Point.jianPoint(a1, a)), t);
       return Point.addPoint(a, temp);
   }

   // 获取直线的交叉点，若两条线平行，返回null。
   public Point getIntersection(Line l) {
       // LineInputError.isParallelError(this, l);
       if (this.isParallel(l)) {
           return null;
       }
       if (p1.equals(l.p1) || p1.equals(l.p2)) {
           return p1;
       }
       if (p2.equals(l.p1) || p2.equals(l.p2)) {
           return p2;
       }
       Point p3 = l.p1, p4 = l.p2;
       double x_member, x_denominator, y_member, y_denominator;
       Point cross_point = new Point();
       x_denominator = p4.x * p2.y - p4.x * p1.y - p3.x * p2.y + p3.x * p1.y - p2.x * p4.y + p2.x * p3.y + p1.x * p4.y
               - p1.x * p3.y;

       x_member = p3.y * p4.x * p2.x - p4.y * p3.x * p2.x - p3.y * p4.x * p1.x + p4.y * p3.x * p1.x
               - p1.y * p2.x * p4.x + p2.y * p1.x * p4.x + p1.y * p2.x * p3.x - p2.y * p1.x * p3.x;

       if (x_denominator == 0)
           cross_point.x = 0;
       else
           cross_point.x = x_member / x_denominator;

       y_denominator = p4.y * p2.x - p4.y * p1.x - p3.y * p2.x + p1.x * p3.y - p2.y * p4.x + p2.y * p3.x + p1.y * p4.x
               - p1.y * p3.x;

       y_member = -p3.y * p4.x * p2.y + p4.y * p3.x * p2.y + p3.y * p4.x * p1.y - p4.y * p3.x * p1.y
               + p1.y * p2.x * p4.y - p1.y * p2.x * p3.y - p2.y * p1.x * p4.y + p2.y * p1.x * p3.y;

       if (y_denominator == 0)
           cross_point.y = 0;
       else
           cross_point.y = y_member / y_denominator;

       if (cross_point.getX() == -0.0) cross_point.x = 0.0;
       if (cross_point.getY() == -0.0) cross_point.y = 0.0;

      return cross_point; // 平行返回(0,0)
   }
}