AHUACM寒假集训VI(网络流)
luoguP2472.蜥蜴
题目大意:
\(R\times C(1\leq R,C\leq20)\)的网格上,每个格子有一个高度\(h_{ij}(1\leq h\leq3)\),每次有蜥蜴跳离这个格子,其高度就\(-1\),不能跳入任何高度为\(0\)的格子,蜥蜴在任何时刻也不能够站立在高度为\(0\)的格子上面,一开始一些高度不为\(0\)的格子上面有一些蜥蜴,蜥蜴一次最多跳跃距离为\(d(1\leq d\leq4)\)(欧几里得距离),蜥蜴在跳出网格前每一步都必须待在一个可以站立的柱子上,问最少有多少蜥蜴跳不出网格。
思路:
考虑网络流,源点\(S\)向每个初始有蜥蜴的格点连一条容量为1的边,每个能够跳出网格的格子向汇点\(T\)连一条容量为\(inf\)的边,每个网格向它一步能跳到的网格连一条容量为\(inf\)的边,每个网格的高度\(h_{ij}\)可以视作该点的容量,将其拆为出,入两个点即可,对这张图跑一边最大流,答案就是初始的蜥蜴总数\(-maxflow\)。
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxn = 3000010;
const int maxv = 1010;
int R, C, D;
int high[30][30];
char field[30][30];
struct edge {
int to, cap, rev;
};
vector<edge> G[maxv];
int level[maxv], iter[maxv];
void add_edge(int from, int to, int cap)
{
G[from].push_back(edge{ to,cap,(int)G[to].size() });
G[to].push_back(edge{ from,0,(int)G[from].size() - 1 });
}
void bfs(int s)
{
memset(level, -1, sizeof(level));
queue<int> que;
level[s] = 0;
que.push(s);
while (!que.empty())
{
int v = que.front();
que.pop();
for (int i = 0; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && level[e.to] < 0)
{
level[e.to] = level[v] + 1;
que.push(e.to);
}
}
}
}
int dfs(int v, int t, int f)
{
if (v == t)
return f;
for (int& i = iter[v]; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && level[v] < level[e.to])
{
int d = dfs(e.to, t, min(f, e.cap));
if (d > 0)
{
e.cap -= d;
G[e.to][e.rev].cap += d;
return d;
}
}
}
return 0;
}
int max_flow(int s, int t)
{
int flow = 0;
while (true)
{
bfs(s);
if (level[t] < 0)
return flow;
memset(iter, 0, sizeof(iter));
int f;
while ((f = dfs(s, t, INF)) > 0)
flow += f;
}
return flow;
}
int dis(int x1, int y1, int x2, int y2)
{
return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}
void solve()
{
//(i-1)*C+j:i行j列入
//(j-1)*C+j+R*C:i行j出
int ans = 0;
int S = R * C * 2 + 1, T = R * C * 2 + 2;
for (int i = 1; i <= R; i++)
{
for (int j = 1; j <= C; j++)
{
if (high[i][j] > 0)
{
int v = (i - 1) * C + j;
add_edge(v, v + R * C, high[i][j]);
for (int k = 1; k <= R; k++)
{
for (int l = 1; l <= C; l++)
{
int u = (k - 1) * C + l;
if (dis(i, j, k, l) <= D * D && !(k == i && l == j) && high[k][l] > 0)
add_edge(v + R * C, u, inf);
}
}
if (field[i][j] == 'L')
{
add_edge(S, v, 1);
ans++;
}
if (i <= D || i + D > R || j <= D || j + D > C)
add_edge(v + R * C, T, inf);
}
}
}
cout << ans - max_flow(S, T) << endl;
}
int main()
{
IOS;
char tmp;
cin >> R >> C >> D;
for (int i = 1; i <= R; i++)
{
for (int j = 1; j <= C; j++)
{
cin >> tmp;
high[i][j] = tmp - '0';
}
}
for(int i = 1; i <= R; i++)
{
for (int j = 1; j <= C; j++)
cin >> field[i][j];
}
solve();
return 0;
}
luoguP2053.修车
题目大意:
\(N(N\leq60)\)辆车,\(M(M\leq9)\)个修理工,第\(i\)辆车在第\(j\)个修理工处需要的修复时间为\(T_{ij}\),使所有车辆全部修复完毕所花费的平均时间最少(包括等待时间以及修理时间)。
思路:
平均时间最少也就是要最小化总时间,考虑在某个修理工处的一个修车安排的总时间是如何产生的。设一个修理工处的总时间为\(A\),修理的车辆先后为\(N_{1},N_{2},N_{3}\),于是就有\(A=N_{1}+(N_{1}+N_{2})+(N_{1}+N_{2}+N_{3})\),即\(A=N_{3}+2N_{2}+3N_{1}\),于是可以看出一个修理工处如果修\(k\)辆车,那么相当于所修里的车分别花费\(1\sim k\)倍的时间,于是我们对于每个修理工,可以将其拆为\(N\)个点,表示花费\(1\sim N\)倍的时间,将这\(NM\)个点向汇点\(T\)连容量为\(1\),费用\(0\)的边。之后对于每辆车,向每个修理工及其各倍数的点连一条容量为\(1\),费用为\(T_{ij}\times\)倍数的边,再从源点\(S\)向每辆车连容量为\(1\),费用为\(0\)的边,之后在这张图上跑流量为\(N\)的最小费用流即可求出最少的总时间。
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxv = 4010;
struct edge {
int to, cap, cost, rev;
};
int V;//顶点数
vector<edge> G[maxv];
int h[maxv], dist[maxv], prevv[maxv], preve[maxv];
void add_edge(int from, int to, int cap, int cost)
{
G[from].push_back(edge{ to, cap, cost, (int)G[to].size() });
G[to].push_back(edge{ from, 0, -cost, (int)G[from].size() - 1 });
}
int min_cost_flow(int s, int t, int f)//求s->t,f流之最小费用流,若不能再增广,返回-1,即无解
{
int res = 0;
memset(h, 0, sizeof(h));
while (f > 0)
{
priority_queue<PII, vector<PII>, greater<PII>> que;
memset(dist, inf, sizeof(dist));
dist[s] = 0;
que.push(PII(0, s));
while (!que.empty())
{
PII p = que.top();
que.pop();
int v = p.second;
if (dist[v] < p.first)
continue;
for (int i = 0; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && dist[e.to] > dist[v] + e.cost + h[v] - h[e.to])
{
dist[e.to] = dist[v] + e.cost + h[v] - h[e.to];
prevv[e.to] = v;
preve[e.to] = i;
que.push(PII(dist[e.to], e.to));
}
}
}
if (dist[t] == inf)
return -1;
for (int v = 1; v <= V; v++)
h[v] += dist[v];
int d = f;
for (int v = t; v != s; v = prevv[v])
d = min(d, G[prevv[v]][preve[v]].cap);
f -= d;
res += d * h[t];
for (int v = t; v != s; v = prevv[v])
{
edge& e = G[prevv[v]][preve[v]];
e.cap -= d;
G[v][e.rev].cap += d;
}
}
return res;
}
int N, M, C[70][20];
void solve()
{
//1~N:顾客
//k*N+1~(k+1)*N:k号修理工
int S = N * (M + 1) + 1, T = S + 1;
V = T;
for (int i = 1; i <= N; i++)
add_edge(S, i, 1, 0);
for (int i = 1; i <= M; i++)
{
for (int j = 1; j <= N; j++)
{
add_edge(i * N + j, T, 1, 0);
for (int k = 1; k <= N; k++)
add_edge(k, i * N + j, 1, C[k][i] * j);
}
}
cout << setiosflags(ios::fixed) << setprecision(2) << (double)min_cost_flow(S, T, N) / N << endl;
}
int main()
{
IOS;
cin >> M >> N;
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
cin >> C[i][j];
}
solve();
return 0;
}
luoguP3227.切糕
题目大意:
一个\(P\times Q\times R(1\leq P,Q,R\leq40)\)的长方体点阵,每个点\((x,y,z)\)上面有一个权值\(v(x,y,z)\),在每个\((x.y)\)处,选择且仅选择一个\(z\)值,获取权值\(v(x,y,z)\),但是在与\((x,y)\)相邻的坐标(\(4\)个方向)处所选择的\(z\)值与在\((x,y)\)处所选择的相差不能超过\(D\),求可以获得的最小总权值。
思路:
考虑没有限制\(D\)的时候,显然直接在每个\((x,y)\)处直接取\(v(x,y,z)\)最小的\(z\)即可,这样的选择亦可以转化为一个最小割模型,即对点阵中所有的点建点,从源点\(S\)向每个\((x,y,1)\)对应的点连一条容量为\(inf\)的边,之后对所有\((x,y,R)\)对应的点向汇点\(T\)连一条容量为\(v(x,y,R)\)的边,再对剩下的所有\((x,y,z)\)对应的点向\((x,y,z+1)\)对应的点连一条容量为\(v(x,y,z)\)的边即可。因为这样建图相当于每一个\((x,y)\)上都必须割去一个边,于是该图的最小割就是没有限制的情况下的答案了。
再考虑有约束\(D\)的情况,我们只需要再刚才的图上再加入几条新的边,即当\(z>D\)时,对所有的\((x,y,z)\)对应的点向其所有相邻坐标对应的\(z-D\)高度的点连一条容量为\(inf\)的边即可,加完这些边的新图的最小割就是带有限制的情况下的答案了。
设\(D=1\),下图的红色边是一条新加的边,这条边可以保证蓝色和紫色的两条边不会同时在最小割中被割去,因为如果同时割去,那么至少还要再割去一条\(S\to 1\to 2\to 3\)或者\(5\to 6\to S\)上的一条边,那么显然直接放弃紫色或者蓝色的边显然割会更小。
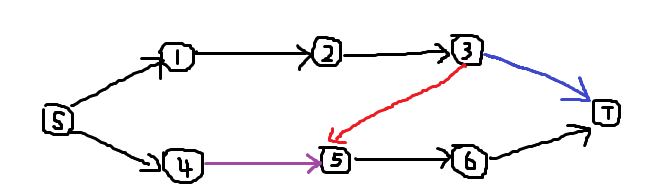
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxv = 70010;
struct edge {
int to, cap, rev;
};
vector<edge> G[maxv];
int level[maxv], iter[maxv];
int P, Q, R, D;
int V[50][50][50];
int di[4] = { 0,0,1,-1 };
int dj[4] = { 1,-1,0,0 };
void add_edge(int from, int to, int cap)
{
G[from].push_back(edge{ to,cap,(int)G[to].size() });
G[to].push_back(edge{ from,0,(int)G[from].size() - 1 });
}
void bfs(int s)
{
memset(level, -1, sizeof(level));
queue<int> que;
level[s] = 0;
que.push(s);
while (!que.empty())
{
int v = que.front();
que.pop();
for (int i = 0; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && level[e.to] < 0)
{
level[e.to] = level[v] + 1;
que.push(e.to);
}
}
}
}
int dfs(int v, int t, int f)
{
if (v == t)
return f;
for (int& i = iter[v]; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && level[v] < level[e.to])
{
int d = dfs(e.to, t, min(f, e.cap));
if (d > 0)
{
e.cap -= d;
G[e.to][e.rev].cap += d;
return d;
}
}
}
return 0;
}
int max_flow(int s, int t)
{
int flow = 0;
while (true)
{
bfs(s);
if (level[t] < 0)
return flow;
memset(iter, 0, sizeof(iter));
int f;
while ((f = dfs(s, t, inf)) > 0)
flow += f;
}
return flow;
}
inline int getnum(int i, int j, int k)
{
return P * Q * (k - 1) + Q * (i - 1) + j;
}
void solve()
{
int S = P * Q * R + 1, T = S + 1;
for (int i = 1; i <= P; i++)
{
for (int j = 1; j <= Q; j++)
{
for (int k = 1; k <= R; k++)
{
int v = getnum(i, j, k), u = getnum(i, j, k + 1);
if (k == 1)
add_edge(S, v, inf);
if (k == R)
add_edge(v, T, V[i][j][k]);
else
add_edge(v, u, V[i][j][k]);
if (k > D)
{
for (int l = 0; l < 4; l++)
{
int ni = i + di[l], nj = j + dj[l];
if (ni >= 1 && ni <= P && nj >= 1 && nj <= Q)
add_edge(v, getnum(ni, nj, k - D), inf);
}
}
}
}
}
cout << max_flow(S, T) << endl;
}
int main()
{
IOS;
cin >> P >> Q >> R >> D;
for (int i = 1; i <= R; i++)
{
for (int j = 1; j <= P; j++)
{
for (int k = 1; k <= Q; k++)
cin >> V[j][k][i];
}
}
solve();
return 0;
}
luoguP4174.最大获利
题目大意:
\(N(N\leq 5000)\)个基站,每个基站建设成本\(P_{i}(0\leq P_{i}\leq 100)\),\(M(M\leq50000)\)个用户,第\(i\)个用户希望使用\(A_{i}\),\(B_{i}\)两个基站,给使用费\(C_{i}(0\leq C_{i}\leq 100)\)。可以选择架设若干基站来满足若干用户的建设需求,求最大的收益(费用-成本)。
思路:
考虑获取某个使用费\(C_{i}\),那么就需要建设\(A_{i},B_{i}\),于是可以从\(C_{i}\)向\(A_{i},B_{i}\)连边。每个点有各自的权值,成本为负的,使用费为正的,于是对于所有\(C\)如此连边,求这张图的最大权闭合子图即可。
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxm = 50010;
const int maxn = 5010;
struct edge {
int to, cap, rev;
};
int N, M;
int P[maxn], A[maxm], B[maxm], C[maxm];
vector<edge>G[maxm * 3];
int level[maxm * 3], iter[maxm * 3];
LL sum = 0;
void add_edge(int from, int to, int cap)
{
G[from].push_back(edge{ to,cap,(int)G[to].size() });
G[to].push_back(edge{ from,0,(int)G[from].size() - 1 });
}
void bfs(int s)
{
memset(level, -1, sizeof(level));
queue<int> que;
level[s] = 0;
que.push(s);
while (!que.empty())
{
int v = que.front();
que.pop();
for (int i = 0; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && level[e.to] < 0)
{
level[e.to] = level[v] + 1;
que.push(e.to);
}
}
}
}
int dfs(int v, int t, int f)
{
if (v == t)
return f;
for (int& i = iter[v]; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && level[v] < level[e.to])
{
int d = dfs(e.to, t, min(f, e.cap));
if (d > 0)
{
e.cap -= d;
G[e.to][e.rev].cap += d;
return d;
}
}
}
return 0;
}
int max_flow(int s, int t)
{
int flow = 0;
while (true)
{
bfs(s);
if (level[t] < 0)
return flow;
memset(iter, 0, sizeof(iter));
int f;
while ((f = dfs(s, t, INF)) > 0)
flow += f;
}
return flow;
}
void solve()
{
//1~N:基站1~N
//N+1~N+M:各获益
int S = N + M + 1, T = N + M + 2;
for (int i = 1; i <= N; i++)
add_edge(i, T, P[i]);
for (int i = 1; i <= M; i++)
{
add_edge(N + i, B[i], inf);
add_edge(N + i, A[i], inf);
add_edge(S, N + i, C[i]);
}
cout << sum - max_flow(S, T) << endl;
}
int main()
{
IOS;
cin >> N >> M;
for (int i = 1; i <= N; i++)
cin >> P[i];
for (int i = 1; i <= M; i++)
{
cin >> A[i] >> B[i] >> C[i];
sum += C[i];
}
solve();
return 0;
}
CF653D.Delivery Bears
题目大意:
\(N(2\leq N\leq50)\)个点,\(M(1\leq M\leq500)\)条边的有向图,每条边有重量上限\(C_{i}(1\leq C_{i}\leq10^6)\),现有\(X(1\leq X\leq10^5)\)批重量相同的货物,你可以给定任意的重量,但是一批货物必须作为一个整体运送(即不能拆成若干重量更小的货物运送),求能够将全部\(X\)批货物从\(1\)运送到\(N\)的时的货物总重量最大为多少。
思路:
显然我们可以二分每批货物的重量\(w\),对于每个\(w\),我们将图中所有的权值由\(C_{i}\)变为\(\lfloor \frac{C_{i}}{w}\rfloor\),之后在图中跑最大流,如果\(maxflow\geq X\)就说明当前重量可行,否则不可行。
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxv = 60;
const int maxe = 510;
int N, M, X;
LL C[maxe];
int U[maxe], V[maxe];
struct edge {
int to;
LL cap;
int rev;
};
vector<edge> G[maxv];
int level[maxv], iter[maxv];
void add_edge(int from, int to, LL cap)
{
G[from].push_back(edge{ to,cap,(int)G[to].size() });
G[to].push_back(edge{ from,0,(int)G[from].size() - 1 });
}
void bfs(int s)
{
memset(level, -1, sizeof(level));
queue<int> que;
level[s] = 0;
que.push(s);
while (!que.empty())
{
int v = que.front();
que.pop();
for (int i = 0; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && level[e.to] < 0)
{
level[e.to] = level[v] + 1;
que.push(e.to);
}
}
}
}
int dfs(int v, int t, LL f)
{
if (v == t)
return f;
for (int& i = iter[v]; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && level[v] < level[e.to])
{
LL d = dfs(e.to, t, min(f, e.cap));
if (d > 0)
{
e.cap -= d;
G[e.to][e.rev].cap += d;
return d;
}
}
}
return 0;
}
LL max_flow(int s, int t)
{
LL flow = 0;
while (true)
{
bfs(s);
if (level[t] < 0)
return flow;
memset(iter, 0, sizeof(iter));
LL f;
while ((f = dfs(s, t, INF)) > 0)
flow += f;
}
return flow;
}
bool Check(double w)
{
for (int i = 1; i <= N; i++)
G[i].clear();
for (int i = 1; i <= M; i++)
add_edge(U[i], V[i], (LL)floor(C[i] / w));
return max_flow(1, N) >= X;
}
void solve()
{
double lo = 0, hi = INF;
for (int i = 1; i <= 100; i++)
{
double mid = (lo + hi) / 2;
if (Check(mid))
lo = mid;
else
hi = mid;
}
double ans = lo * X;
cout << setiosflags(ios::fixed) << setprecision(10) << ans << endl;
}
int main()
{
IOS;
cin >> N >> M >> X;
for (int i = 1; i <= M; i++)
cin >> U[i] >> V[i] >> C[i];
solve();
return 0;
}
luoguP4043.支线剧情
题目大意:
给定一张\(N(N\leq300)\)个点,\(M(M\leq15000)\)的\(DAG\),每条边上有一个费用,可以从\(1\)号点出发若干次,每次可以在任意一个点结束,求使将所有边都走过一遍所花费的最小费用。
思路:
建立源点\(S\)与汇点\(T\),\(S\)向\(1\)连一条容量为\(inf\),费用为\(0\)的边,表示可以从\(1\)出发若干次,\(1\sim N\)每个点向\(T\)连容量为\(inf\),费用为\(0\)的边,表示可以从任意一点结束若干次,对于原图中已经存在的边,连一条容量为\([1,inf]\),费用为原费用的边,表示所有边至少走\(1\)次。之后就是要求新图的最小费用可行流,建立超级源点\(SS\)与超级汇点\(ST\),对所有有上界\(c\),下界\(b\)的边\((u,v)\),从\(u\)到\(v\)连容量为\(c-b\)的边,从\(u\)向\(TT\)连容量为\(1\)的边,从\(SS\)向\(v\)连容量为\(1\)的边,这些边的费用\(d\)保持不变,最后再从\(T\)向\(S\)连一条容量为\(inf\),费用为\(0\)的边即可。之后求新图的最小费用最大流的费用\(-\)所有有上下界的边的费用总和即可。
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxv = 5010;
struct edge {
int to, cap, cost, rev;
};
int sum = 0;
int N, SS, TT, S, T;
int V;
vector<edge> G[maxv];
int h[maxv], dist[maxv], prevv[maxv], preve[maxv];
void add_edge(int from, int to, int cap, int cost)
{
G[from].push_back(edge{ to, cap, cost, (int)G[to].size() });
G[to].push_back(edge{ from, 0, -cost, (int)G[from].size() - 1 });
}
int min_cost_flow(int s, int t, int f)
{
int res = 0;
memset(h, 0, sizeof(h));
while (f > 0)
{
priority_queue<PII, vector<PII>, greater<PII>> que;
memset(dist, inf, sizeof(dist));
dist[s] = 0;
que.push(PII(0, s));
while (!que.empty())
{
PII p = que.top();
que.pop();
int v = p.second;
if (dist[v] < p.first)
continue;
for (int i = 0; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && dist[e.to] > dist[v] + e.cost + h[v] - h[e.to])
{
dist[e.to] = dist[v] + e.cost + h[v] - h[e.to];
prevv[e.to] = v;
preve[e.to] = i;
que.push(PII(dist[e.to], e.to));
}
}
}
if (dist[t] == inf)
break;
for (int v = 1; v <= V; v++)
h[v] += dist[v];
int d = f;
for (int v = t; v != s; v = prevv[v])
d = min(d, G[prevv[v]][preve[v]].cap);
f -= d;
res += d * h[t];
for (int v = t; v != s; v = prevv[v])
{
edge& e = G[prevv[v]][preve[v]];
e.cap -= d;
G[v][e.rev].cap += d;
}
}
return res;
}
void solve()
{
cout << min_cost_flow(SS, TT, INT_MAX) - sum << endl;
}
int main()
{
IOS;
cin >> N;
S = N + 1, T = S + 1;
SS = T + 1, V = TT = SS + 1;
int k, to, c;
add_edge(S, 1, inf, 0);
add_edge(T, S, inf, 0);
for (int i = 1; i <= N; i++)
{
add_edge(i, T, inf, 0);
cin >> k;
for (int j = 1; j <= k; j++)
{
cin >> to >> c;
sum += c;
add_edge(i, to, inf - 1, c);
add_edge(SS, to, 1, c);
add_edge(i, TT, 1, c);
}
}
solve();
return 0;
}
luoguP3980.志愿者招募
题目大意:
一向工作持续\(N(1\leq N\leq1000)\)天,共有\(M(1\leq M\leq10000)\)类志愿者,每个志愿者有属性\(s_{i},t_{i},c_{i}\),表示第\(i\)类志愿者在\([s_{i},t_{i}]\)这段时间内参与工作,招募一名该类志愿者需要花费\(c_{i}\)元,每个日期\(i\)需要的志愿者总数至少为\(A_{i}\),求最少花费。
思路:
我们设第\(i\)天参与工作的志愿者总数为\(P_{i}\),招募的第\(j\)类志愿者总数为\(X_{j}\),设第\(j\)类志愿者是否可以在第\(i\)天工作为\(m_{ij}\),于是有\(P_{i}=\sum_{m_{ij}=1} X_{j}\geq A_{i}\),我们设\(Y_{i}\)为第\(i\)天多招募的人数,因此\(A_{i}=\sum_{m_{ij}=1} X_{j}-Y_{i}\),我们可以得到这样的\(N\)个等式。
之后我们对它们做差分,设\(A_{0}=A_{N+1}=0\),求出所有的\(A_{i}-A_{i-1}(1\leq i\leq N+1)\),又对于每类志愿者,其工作时间是连续的一段,因此,每个\(X_{j}\)也是在连续的一段等式中所出现的,因此在差分后的\(N+1\)个等式中,\(X_{j}\)与\(-X_{j}\)各仅出现\(1\)次。同时可以发现,\(Y_{i}\)与\(-Y_{i}\)也各仅出现\(1\)次。我们可以把这每个等式两侧当成一个节点的流出与流入。这样我们可以为每个等式建立一个节点来建图:
对于每个节点\(i\),我们将等式左侧的\(A_{i}-A_{i-1}\)作为其流入,从源点\(S\)向其连一条容量为\(A_{i}-A_{i-1}\)费用为\(0\)的边(如果值为负数,改为向汇点\(T\)连容量为相反数的边),将等式右侧作为流出,由于签面提到的\(X,Y\)的性质,我们可对每个\(X,Y\)仅需对应连一条边(仅对应一个流入和流出),对于每个\(X_{i}\),我们连一条从\(s_{i}\)到\(t_{i}+1\)连一条容量为\(inf\),费用为\(c_{i}\)的边表示\(X_{i}\);而对于每个\(Y_{i}\),我们连一条从\(i\)到\(i-1\)连一条容量为\(inf\),费用为\(0\)的边表示\(Y_{i-1}\)。之后对这样的一张图求最小费用最大流即可。
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxv = 1010;
const int maxn = 1010;
struct edge {
int to, cap, cost, rev;
};
int sum = 0;
int N, M, S, T;
int V;//顶点数
int A[maxn];
vector<edge> G[maxv];
int h[maxv], dist[maxv], prevv[maxv], preve[maxv];
void add_edge(int from, int to, int cap, int cost)
{
//cout << from << "__" << to << "___" << cap << "__" << cost << endl;
G[from].push_back(edge{ to, cap, cost, (int)G[to].size() });
G[to].push_back(edge{ from, 0, -cost, (int)G[from].size() - 1 });
}
int min_cost_flow(int s, int t, int f)
{
int res = 0;
memset(h, 0, sizeof(h));
while (f > 0)
{
priority_queue<PII, vector<PII>, greater<PII>> que;
memset(dist, inf, sizeof(dist));
dist[s] = 0;
que.push(PII(0, s));
while (!que.empty())
{
PII p = que.top();
que.pop();
int v = p.second;
if (dist[v] < p.first)
continue;
for (int i = 0; i < G[v].size(); i++)
{
edge& e = G[v][i];
if (e.cap > 0 && dist[e.to] > dist[v] + e.cost + h[v] - h[e.to])
{
dist[e.to] = dist[v] + e.cost + h[v] - h[e.to];
prevv[e.to] = v;
preve[e.to] = i;
que.push(PII(dist[e.to], e.to));
}
}
}
if (dist[t] == inf)
break;
for (int v = 1; v <= V; v++)
h[v] += dist[v];
int d = f;
for (int v = t; v != s; v = prevv[v])
d = min(d, G[prevv[v]][preve[v]].cap);
f -= d;
res += d * h[t];
for (int v = t; v != s; v = prevv[v])
{
edge& e = G[prevv[v]][preve[v]];
e.cap -= d;
G[v][e.rev].cap += d;
}
}
return res;
}
void solve()
{
cout << min_cost_flow(S, T, inf) << endl;
}
int main()
{
IOS;
cin >> N >> M;
S = N + 2, V = T = S + 1;
for (int i = 1; i <= N; i++)
{
cin >> A[i];
int k = A[i] - A[i - 1];
if (k > 0)
add_edge(S, i, k, 0);
else
add_edge(i, T, -k, 0);
add_edge(i + 1, i, inf, 0);
}
add_edge(N + 1, T, A[N], 0);
int s, t, c;
for (int i = 1; i <= M; i++)
{
cin >> s >> t >> c;
add_edge(s, t + 1, inf, c);
}
solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号