CF873D Merge Sort
其实最优的方法其他的题解已经讲得很好了,本题解仅用于记录和分享一个新的思路。
这道题是让你输出符合条件的序列,而序列的每个数之间具有一定的逻辑关系,很容易想到拓扑排序,于是此题就变为,如何找出满足条件的逻辑关系。
我们可以先看一下操作次数最多的序列:
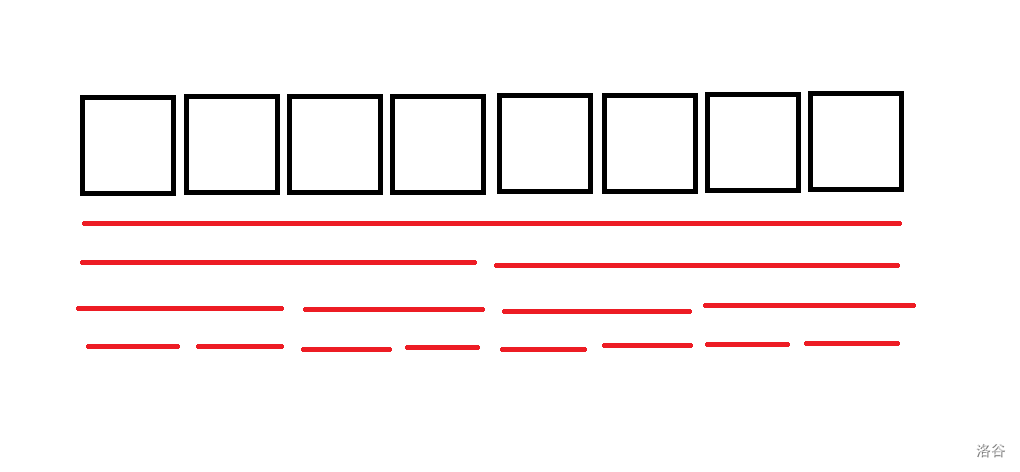
(每一条红线都是一次操作),我们可以删除一次操作,当且仅当左半边与右半边都排好序的情况下,即删除了所有子操作的情况下,使得左半边与右半边中间建一条边,如图:
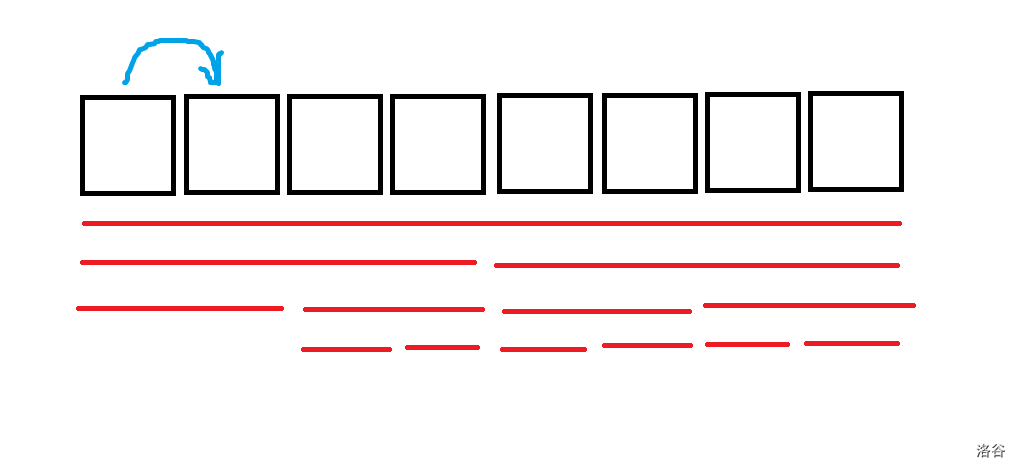
我们可以通过在\(1\)与\(2\)之间建一条边来删除\(1\)与\(2\)两者的操作
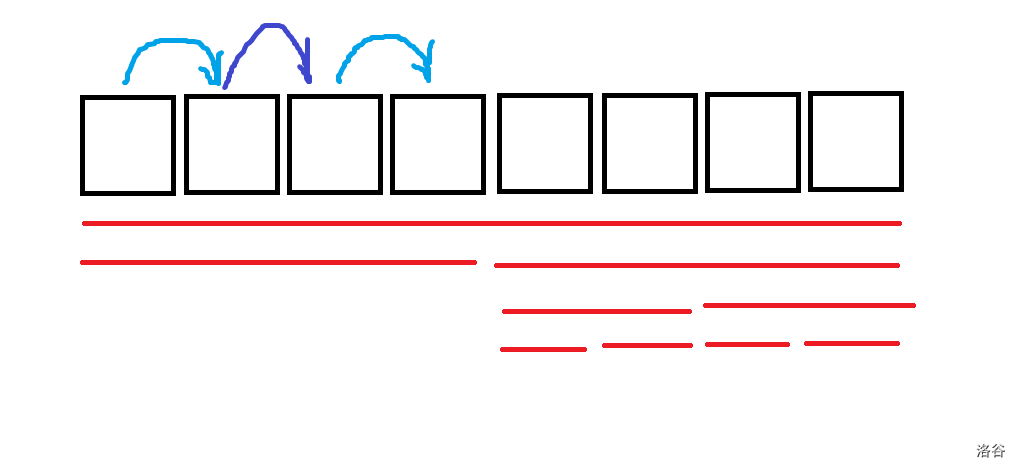
我们还可以通过在\(2\)与\(3\)之间建一条边来删除\(1\)与\(2\)之间,\(3\)与\(4\)之间的操作,但此时\(1\)与\(2\),\(3\)与\(4\)之间必须已经建边。
上述操作可以通过递归完成,最后再跑一边拓扑排序,复杂度\(O(nlogn)\)
#include<cstdio>
#include<iostream>
#include<queue>
using namespace std;
int n,k;
struct Edge
{
int to,nxt;
}e[100005];
int fir[100005],size;
int d[100005];
void add(int u,int v)
{
e[++size].to=v;
e[size].nxt=fir[u];
fir[u]=size;
++d[v];
}
int cnt;
void merge(int l,int r)
{
if(l==r-1)
{
return ;
}
int mid=(l+r)/2;
merge(l,mid);
merge(mid,r);
if(cnt>k)
{
add(mid-1,mid);
cnt-=2;
}
}
queue <int> q;
int ans[100005];
void top()
{
for(int i=n-1;i>=0;--i)
{
if(d[i]==0)
q.push(i);
}//一定要反向塞入,拓扑排序仅能保证逻辑关系,本题顺序非正即反,所以未建边的位置就是反的
cnt=0;
while(q.size())
{
int tmp=q.front();
q.pop();
ans[tmp+1]=++cnt;//我们建边和拓扑的是点的位置,根据出队顺序决定数字顺序
for(int i=fir[tmp];i;i=e[i].nxt)
{
--d[e[i].to];
if(d[e[i].to]==0)
q.push(e[i].to);
}
}
}
int main()
{
cin>>n>>k;
if(k%2==0||k>2*n-1)
{
printf("-1\n");
return 0;
}
cnt=2*n-1;
merge(0,n);
top();
for(int i=1;i<=n;++i)
{
printf("%d ",ans[i]);
}
printf("\n");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号