CF1373F Network Coverage

一个奇怪的思路。

在讲解题目之前，我们先来证明一个奇怪的东东：

任何一种的可行状态，必然可以变为一个至少有一个城市不用向上一个网络站获取连接（即该城市自给自足）的可行状态。
先假设有一个全部向左右获取连接的可行状态。

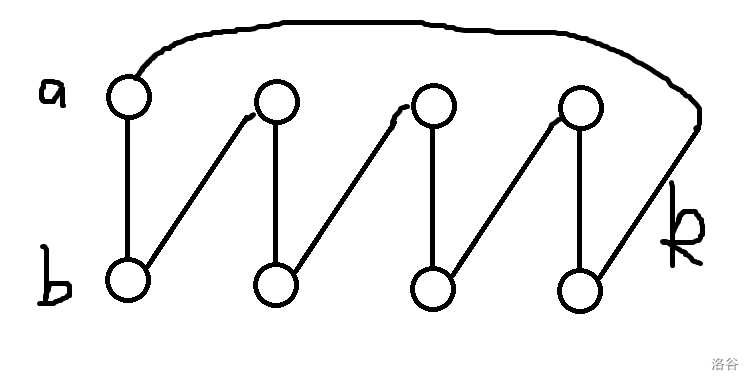
如图，假设k是所有\(bi\)为\(a(i+1)\)提供的连接中最小的一个，我们可以尝试删去\(k\)，那么\(b1\)到\(a1\)就增加了\(k\)，\(b1\)到\(a2\)就减少了一个小于等于\(k\)的数……具体如图：

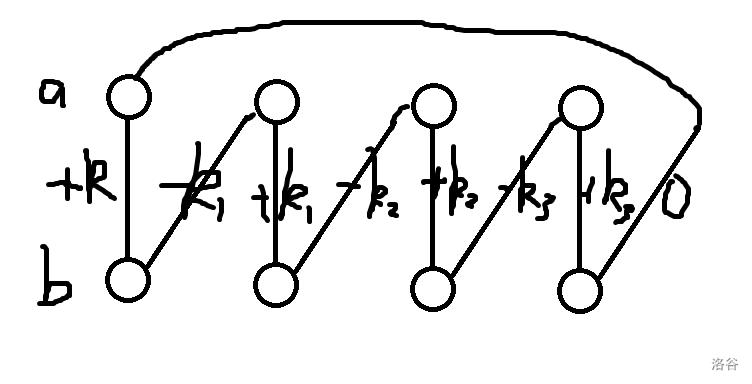
易得，\(k>=k1>=k2>=k3>=k(i-1)>=ki\)，因为\(k\)是其中最小的，所以没有连接会变成负数，也就是说情况依旧合法，由此得证。

因此，我们可以通过寻找这一个不从上一个网络站获取连接的点，再贪心，以消除后效性。因为贪心是线性的，所以我们接下来的问题就是，如何在\(n\)个城市中找出这一个自给自足的城市。

我们可以先看代码：

	for(int i=1;i<=n*2;++i)
	{
		if(b[i-1]-a[i-1]>0)
		a[i]-=b[i-1]-a[i-1];
		a[i]=max(a[i],0);
	}

这一步操作，实际上就是在破环成链后，贪心每个城市，使其能够从上一个网络站获取尽量多的连接，很容易就看出，这样的计算肯定是不全部正确的，因为第一个城市就没有考虑最后一个网络站对他的影响。

（下面的\(ai\)均已减去\(b(i-1)\)给它的连接数）

但是，我们可以判断一种情况，即在考虑\(a(i-1)>b(i-1)\)的情况下，此时，如果再选择将\(b(i-1)\)分给\(ai\)，只会是结果更差，而不能优化答案。如图：

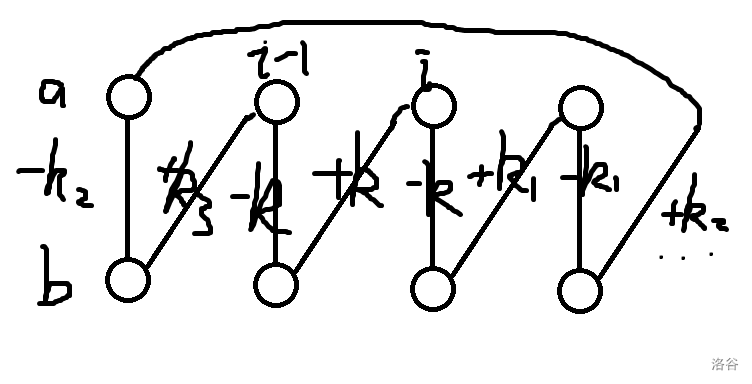
假设\(b(i-1)\)给予\(ai\) \(k\)个连接，我们依旧可以得知\(k>=k1>=k2>=k3>=k(i-1)>=ki\)，同时由于\(a(i-1)>b(i-1)\)，所以\(b(i-1)\)一定是用尽的，如果\(b(i-1)\)需要将\(k\)个连接给\(ai\)，那么\(a(i-1)\)就会少从\(b(i-1)\)获得\(k\)个。针对\(a(i-1)\)，我们可以发现它的连接增加了\(k3\)减少了\(k\)，因为\(k>=k3\)，所以\(a(i-1)\)获得的连接数只会更少，所以结果只能更差或不变。（\(a(i-1)\)本身就是不满足的）

所以我们就变相找到了自给自足的点，即寻找到的第一个\(a(i-1)>b(i-1)\)且\(ai<=bi\)的点。再在该点后贪心即可。

另外，我们可以发现，寻找自给自足的点的代码和贪心的代码实质上是一样的，所以我们可以一起进行。而判断是否成功的依据便是在自给自足点之后是否还有点的\(ai>bi\)，如果有，说明不成功，否则成功。

如还有不理解，可以结合代码食用：

#include<bits/stdc++.h>
using namespace std;
int t;
int n;
int a[4000005];
int b[4000005];
inline int read()
{
	char c=getchar();
	while(c<'0'||'9'<c)
	c=getchar();
	int x=0;
	while('0'<=c&&c<='9')
	{
		x*=10;
		x+=c-'0';
		c=getchar();
	}
	return x;
}
int main()
{
	t=read();
	while(t--)
	{
		n=read();
		for(int i=1;i<=n;++i)
		{
			a[i]=read();
			a[i+n]=a[i];
		}
		for(int i=1;i<=n;++i)
		{
			b[i]=read();
			b[i+n]=b[i];
		}
		if(n==2)
		{
			if(b[1]+b[2]>=a[1]+a[2])
			printf("YES\n");
			else
			printf("NO\n");
			continue;
		}
		for(int i=1;i<=n*2;++i)
		{
			if(b[i-1]-a[i-1]>0)
			a[i]-=b[i-1]-a[i-1];
			a[i]=max(a[i],0);//将判断自给自足点与贪心结合
		}
		bool ok=true;
		for(int i=n+1;i<=n*2;++i)
		{
			ok&=b[i]>=a[i];
		}//因为实际上在找到了自给自足点之后的贪心都是正确的，所以我们只需要随意找一个之后的点即可，而n+1~2n一定是正确的
		if(ok)
		printf("YES\n");
		else
		printf("NO\n");
	}
	return 0;
}

P.S.实际上本方法是在本蒟蒻交了这个奇怪的代码并 \(AC\) 之后才思考出来的思路，所以思路可能会有误，希望各位大佬积极指出。