OUC中国海洋大学2023计算机图形学期末复习笔记

image-20260122202625375

\(\alpha\)

重点导航

第一章 变换

绕任意轴旋转

第二章 光栅化

点是否在三角形内

Z-Buffer算法

第三章 着色

Bling-Phong

第四章 几何

贝塞尔曲线

第五章 光线追踪

Whitted-Style光线追踪算法递归结束条件

AABB包围盒求交

数学基础

点乘的应用

  • 判断两向量方向有多近
  • 求一个向量在另一个向量上的投影
  • 分解一个向量
  • 判断两向量是”同向“还是”逆向“

叉乘的应用

  • 判断左右
  • 判断内外

\[\begin{bmatrix}x_a \\y_a \\z_a\end{bmatrix} \times\begin{bmatrix} x_b \\ y_b \\ z_b\end{bmatrix}=\begin{bmatrix}y_az_b-y_bz_a\\z_ax_b - x_az_b\\x_ay_b - y_ax_b\end{bmatrix} \]

仿射变换

线性变化

这类变化，首先找到x和y怎么变得，得到两个线性表达式。然后将这个表达式切换成矩阵表达就可以了。关键是这四个变换矩阵。

缩放

我们发现 x = ax， b = by。简单

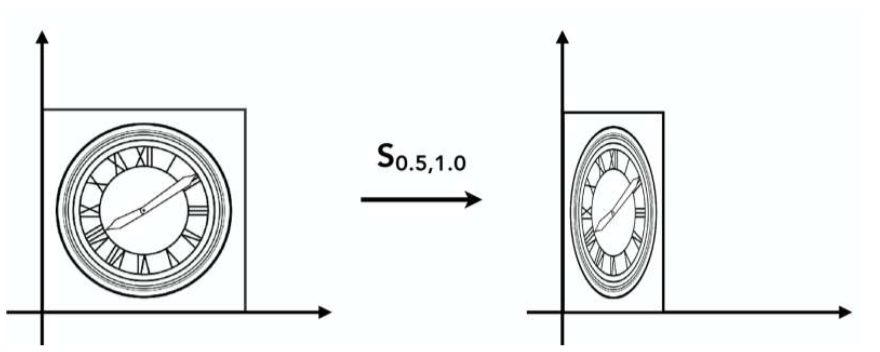
image-20260122204017666

\[\begin{bmatrix}x' \\ y'\end{bmatrix}\quad = \quad \begin{bmatrix} s_x&0 \\0& s_y\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} \]

这个三维也很简单，不说了

对称

y不变，x相反。这是y对称，x对称刚好反着来

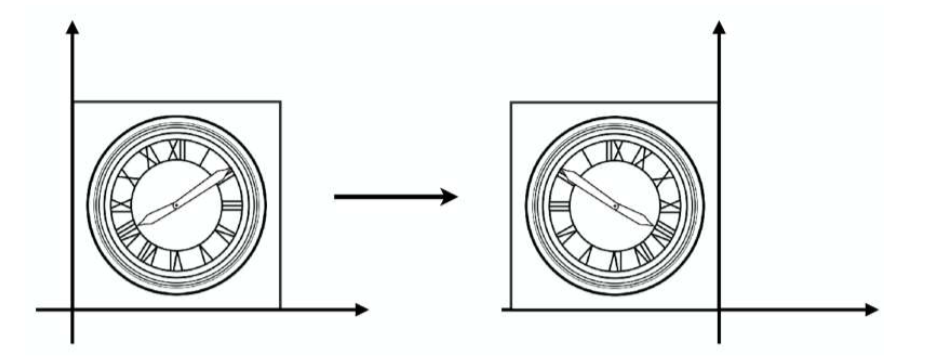
image-20260122204154130

\[\begin{bmatrix}x' \\ y'\end{bmatrix}\quad = \quad\begin{bmatrix}-1& 0\\0 & 1\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} \]

拓展到三维。关于哪个平面对称（比如ZoY），那么平面的两个坐标轴（yz）不变，剩下的一个坐标轴（X）相反即可

错切

我们取特殊点（0，1），错切变换后变成了（a，1）。取（0，0.5），得到（0.5a，0.5）。所以横坐标变成了（原来 + y*a）, 纵坐标不变

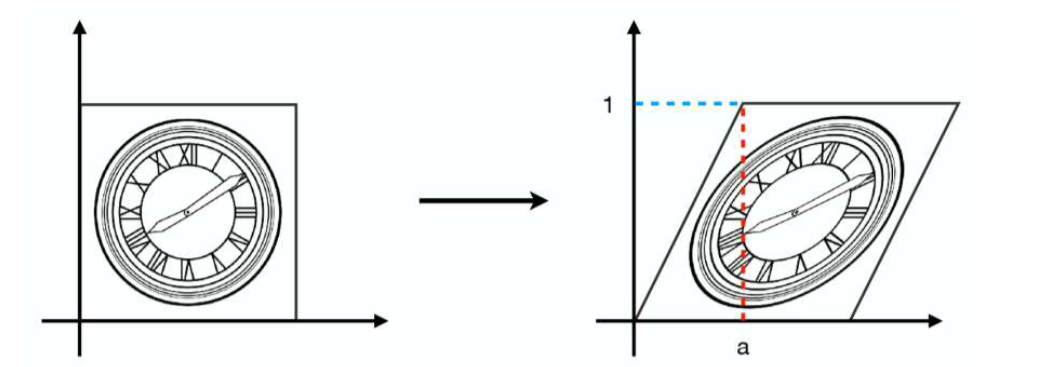
image-20260122204331398

\[\begin{bmatrix}x' \\ y'\end{bmatrix}\quad = \quad\begin{bmatrix}1 & a \\0 & 1\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} \]

旋转

二维

（1，0）变成了（cosα，sinα），

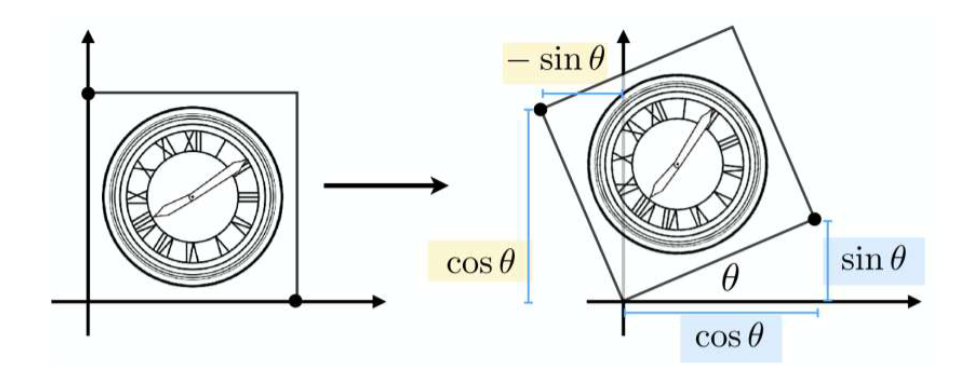
image-20260122205421977

\[\begin{bmatrix}x' \\ y'\end{bmatrix}\quad = \quad\begin{bmatrix}cos\theta & -sin\theta \\sin\theta & cos\theta\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} \]

三维

绕哪个轴旋转，哪个轴不变（横、纵），其余注意：关于Y轴旋转有所不同，取相反（-α）

image-20260122213409255

平移

齐次坐标

第三维是1代表点（x，y，1），第三位是0代表向量（x，y，0）

点 - 点 = 向量

向量 + 向量 = 向量

点 + 向量 = 点

点 + 点 = 点

平移变换

此时x = x+ tx， y = y+ty

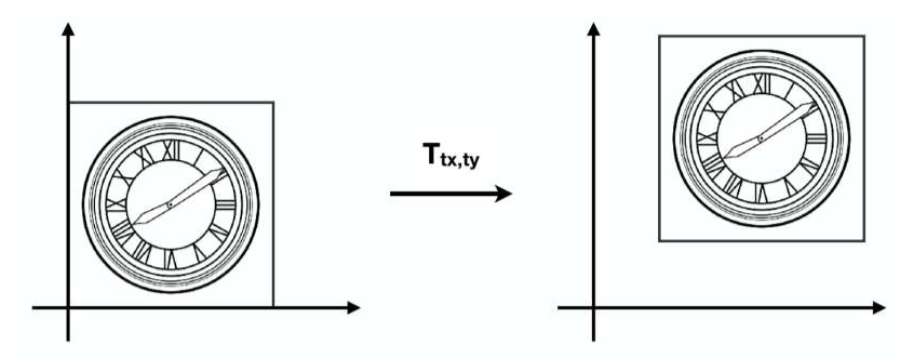
image-20260122210908628

利用齐次坐标，得到以下矩阵

\[\begin{bmatrix}1 & 0 & t_x\\0 & 1 & t_y\\0 & 0 & 1\end{bmatrix} \]

逆变换

旋转矩阵的逆变换

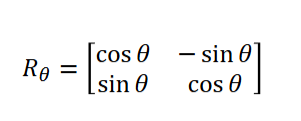
image-20260122211556581

组合变换

顺序很重要，从右往左

image-20260122211818196

例题

绕任意点C的旋转
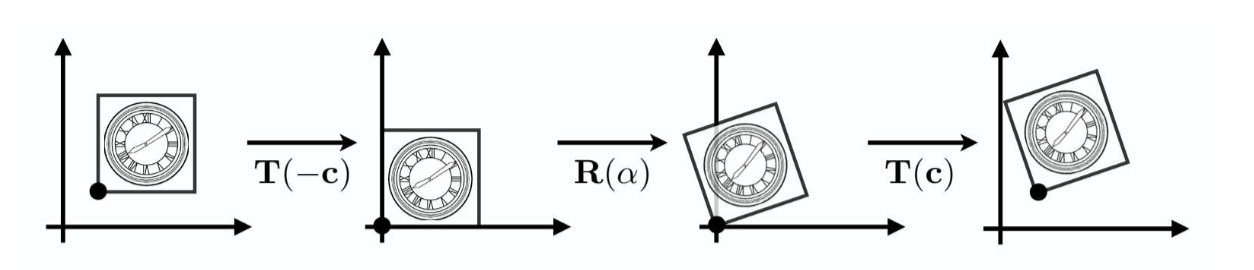
image-20260122211846543

我们先平移到原点，然后进行旋转，最后进行平移的逆运算

绕任意轴旋转
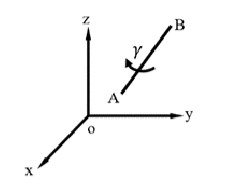
image-20260123134746630

设以三维空间中任意一条线段\(AB\) 为旋转轴，点\(P\)绕\(AB\)逆时针旋转$ γ$ 角，求旋转矩阵\(R_{AB}\)

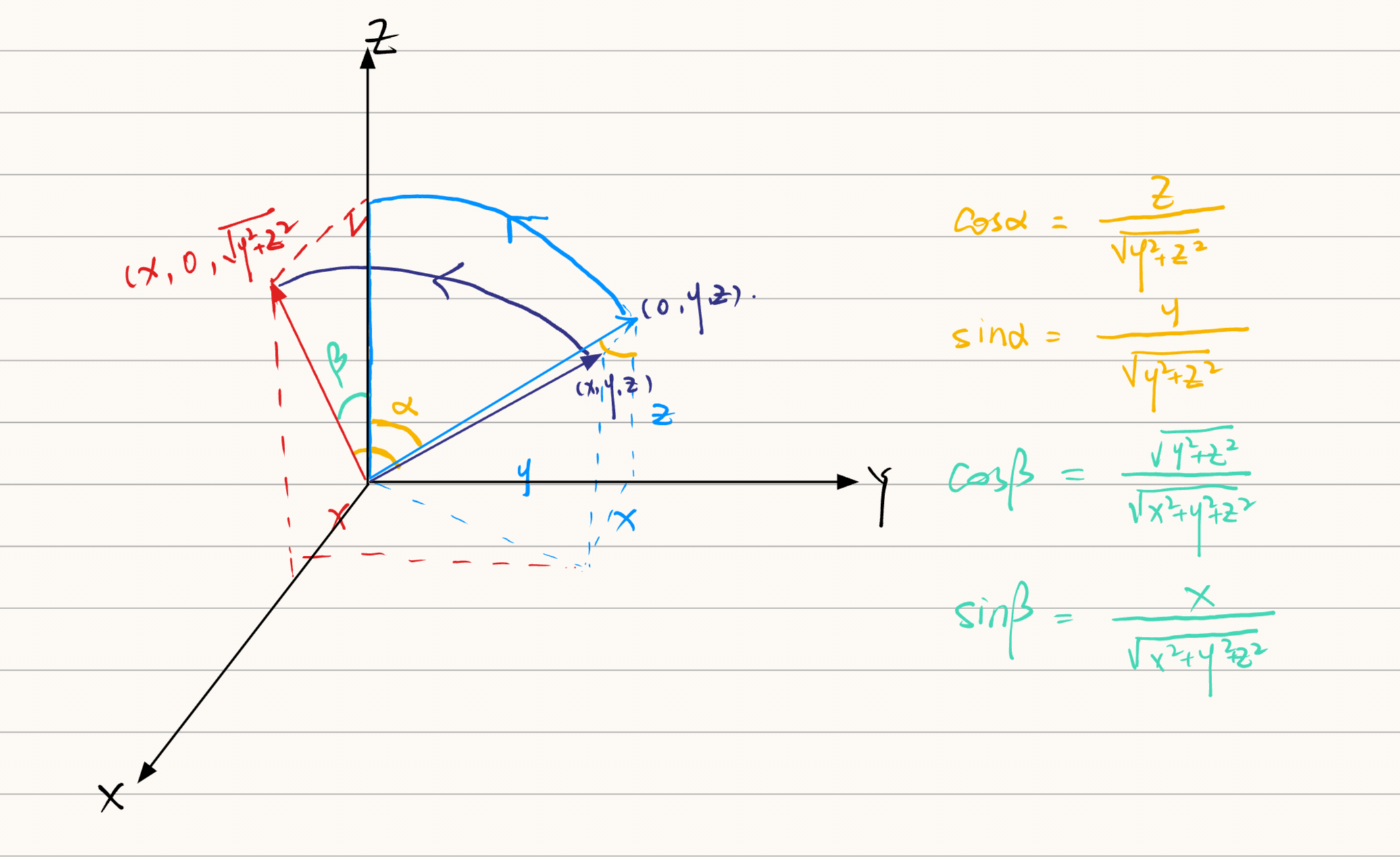
Screenshot_2026-01-23-15-43-34-211_com.orion.notein
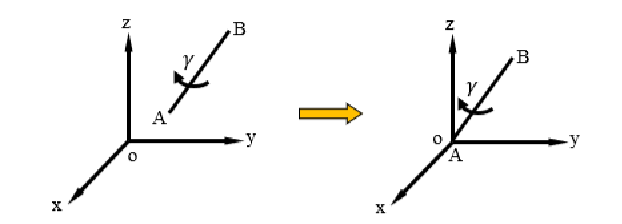
  1. 平移\(AB\) 到坐标原点
image-20260123135318856

\[T=\begin{bmatrix}1 &0 &0 & -x_A\\0 &1 &0 & -y_A\\0 &0 &1 & -z_A\\0 &0 &0 & 1\end{bmatrix} \]

  1. 绕 \(X\) 轴旋转 \(\alpha\) 到 \(ZoX\) 平面上

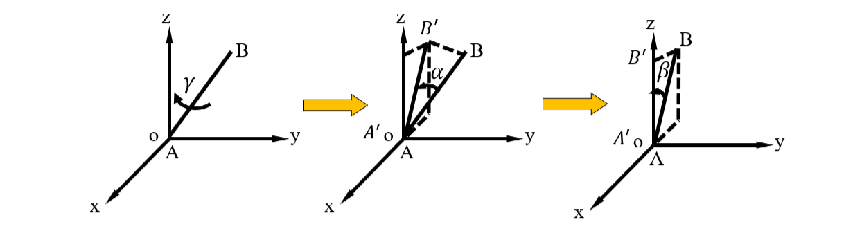
image-20260123145130511

\[R_x =\begin{bmatrix}1 &0 &0 &0\\0&cos\alpha &-sin\alpha &0\\0& sin\alpha&cos\alpha & 0\\0&0 &0 &1\end{bmatrix} \]

这个 α 怎么求呢？ 注意我们这里绕 X 轴旋转，所以在 YoZ 平面上观察。AB绕X轴旋转，投影在YoZ平面上的轨迹是一个圆。所以我们将AB投影到YoZ平面上，当投影的向量和 Z 轴重合的时候， AB就旋转到了 ZoX 平面。

即 cosα = \(\frac{z}{\sqrt{y^2+z^2}}\)

  1. 绕 \(Y\) 轴旋转 \(\beta\) 到 \(Z\) 轴上

\[R_y =\begin{bmatrix}cos\beta& 0& sin\beta&0\\0& 1&0 &0\\-sin\beta& 0&cos\beta &0\\0&0 &0 &1\end{bmatrix} \]

绕X轴旋转，那么X不会变，所以投影到ZoX平面上的新坐标（x’, y', z'）中的x' = x。然后 y‘ = 0，z = \(\sqrt{y^2 + z^2}\)，即z是原向量在YoZ平面投影的模长。

最终我们得到 cosβ = ...

  1. 绕 \(Z\) 轴旋转 $\gamma $ 角

\[R_z =\begin{bmatrix}cos\gamma& -sin\gamma & 0&0\\sin\gamma& cos\gamma& 0&0\\0& 0& 1& 0\\0&0 & 0&1\end{bmatrix} \]

  1. 执行绕 \(Y\) 轴旋转的逆变换，回到 \(ZoX\) 平面上的状态（\(R_y^{-1}\)）

  2. 执行绕 \(X\) 轴旋转的逆变换，回到 \(A\) 在原点的状态（\(R_x^{-1}\)）

  3. 执行平移的逆变换（略）

最后得到总方程组

\[R_{AB} = T^{-1}R_x^{-1}R_y^{-1}R_zR_yR_xT \]

考试的时候当然用上面方法写过程，罗德里格旋转公式算答案

\[V_{rot} = cos\theta \cdot \vec{v} + (1-cos\theta)(\vec{v} \cdot \vec{k}) \cdot \vec{k} + sin\theta \cdot \vec{k} \times \vec{v} \]

其中 v是给的任意向量，k是旋转轴的单位向量

光栅化成像

MVP变换

模型变换

目的：选景、安排好被拍人的位置

包含上面提到的仿射变换

视图变换

目的：找好相机的角度。如果模型和相机的位置都发生变化，如何保证照片不发生变化

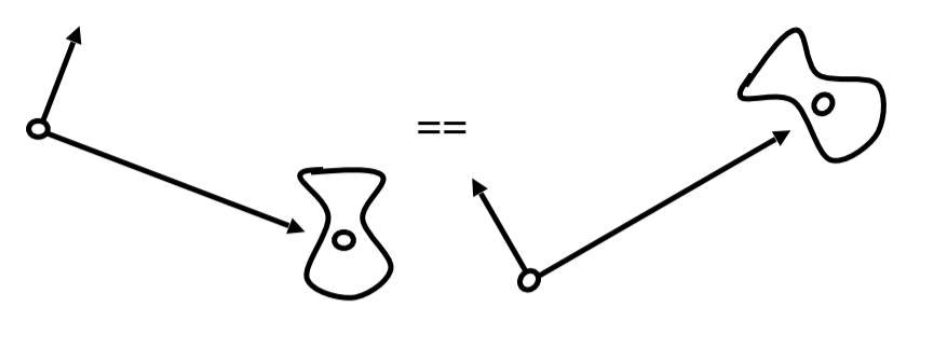
image-20260122215558459

在这里我们做的是 摆正 这个操作

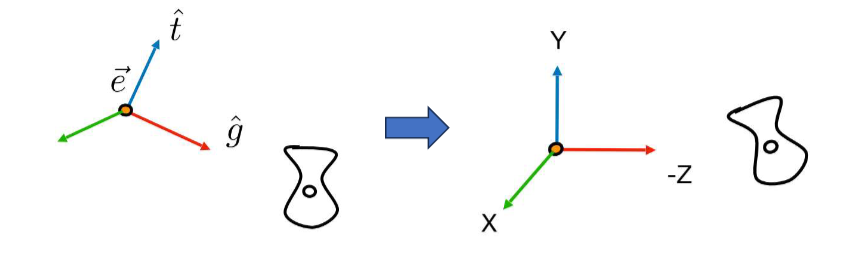
image-20260123190934037
  1. 平移到原点。这里平移距离都是 \(-\vec{e}\) 。
  2. 然后旋转三次

投影变换

目的：拍照

将3D图像变成二维的

正交投影

将相机放在原点，观察方向取 -z，向上方向取Y。

我们舍弃掉Z坐标，将结果平移和缩放到 \([-1, 1]^2\)的矩形内

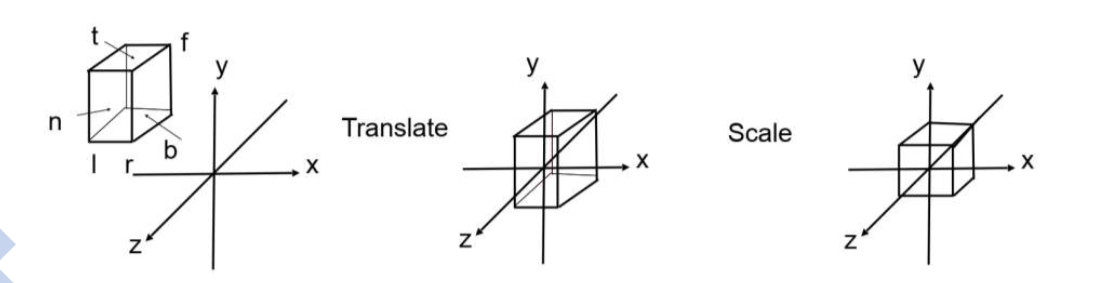
image-20260123191247098

透视投影

有近大远小的效果。平行线不再平行，其延长线相交到一点

我们做的好比把一个截头锥体挤压成一个立方体，然后做正交投影

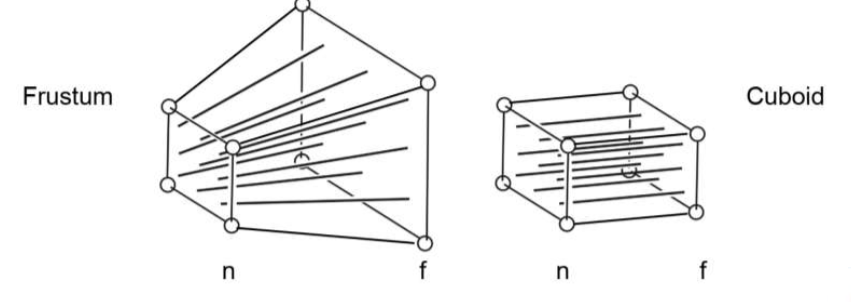
image-20260123191617893

这个矩阵应该不用记

屏幕空间

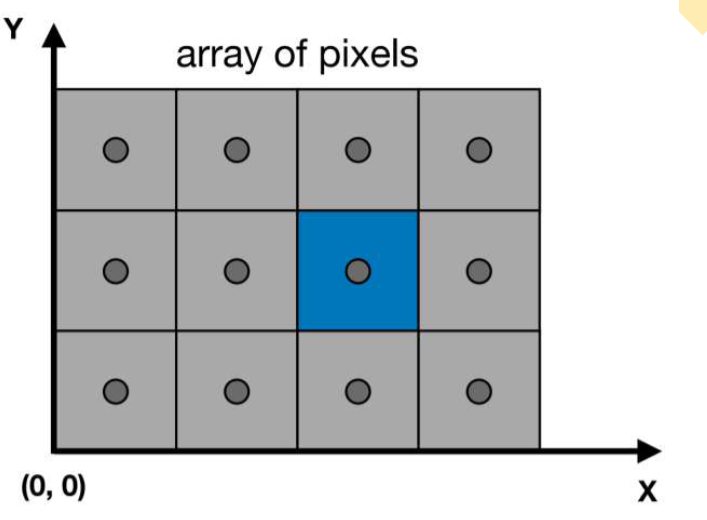
image-20260122215807950

像素索引、像素中心

像素索引位于左下角，由（0，0）到（width-1，height-1）

像素中心相对于索引来说是：（x+0.5， y+0.5）

屏幕覆盖区域

屏幕覆盖的区域由（0，0）到（width，height）

视口变换

将 $[-1, 1]\times [-1,1] $ 切换到屏幕空间$ [0, width] \times [0, height]$. 所以和 Z 坐标无关

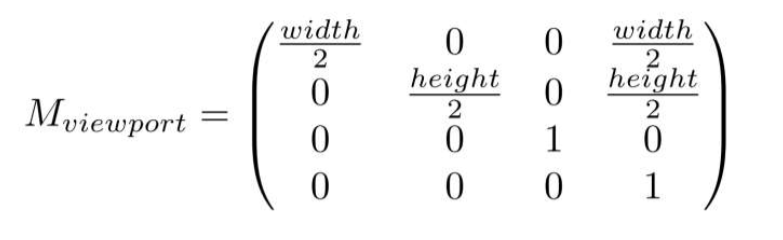
image-20260122220258150

多边形网格

三角网格性质

  • 三角网格一定是平面的

  • 内外定义清晰

  • 对内部的任一点方便做插值

采样——光栅化一个三角形

采样的定义

光栅化的最简单的方法：采样

给定一个连续的函数，在某点计算函数的值（离散化一个函数的过程）

举例

对时间（一维）、面积（二维）、方向（二维）、体积（三维）采样

二维采样
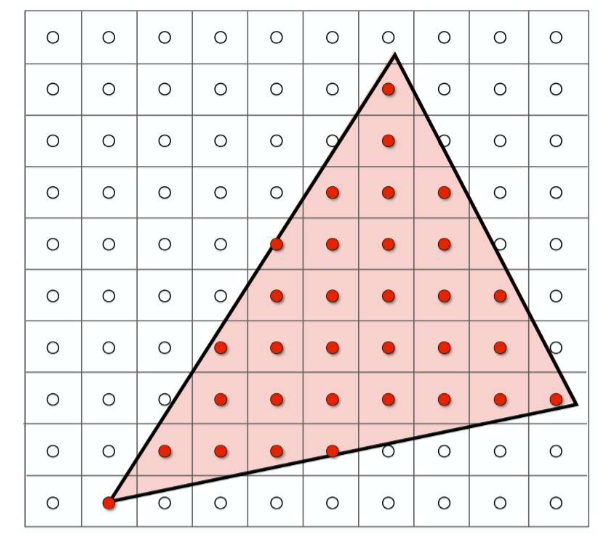
image-20260122221659071
点是否在三角形内
方法一：利用叉乘
image-20260123163610515
方法二：利用重心坐标
image-20260123163632689

走样

常见走样和成因

  • 锯齿：空间采样
  • 摩尔纹：欠采样的图像
  • 车轮错觉：时间采样

如何改善走样问题

信号变换的太快（高频），而采样频率太慢。所以也可以提高采样率来解决走样问题

反走样

原理

在采样前先过滤掉高频信息

方法

光栅化三角形反走样的边界，像素值为中间值。

image-20260122223300067

平均像素值通过三角形覆盖像素面积来计算

超级采样 vs 点采样

通过在一个像素中多次采样，计算他们的平均值作为平均像素值

点采样中一个像素中一个采样点

超级采样中一个像素 N*N个采样点，计算每个像素中N*N个采样点的平均值

遮挡/可见性——光栅化多个三角形

画家算法——由远及近

先画远处的物体，再画近处的物体

  1. 对场景中的多边形按深度进行排序（O(nlogn)）
  2. 按照深度从深到浅绘图
  3. 浅的覆盖到深的，需要再帧缓冲器中重写

Z-Buffer算法

思想

对每个采样点（像素）记录当前的最小Z值。

这里的Z是正的，力相机越近，Z越小

伪代码

我们需要一个帧缓冲器记录颜色值；和一个深度缓冲器记录深度值

for(each triangle T)
	for(each smaple (x,y,z) in T)
		if(z < zbuffer[x,y])
			framebuffer[x,y] = rgb;
			zbuffer[x,y] = z;
        else
    		;
  1. 遍历每个多边形（三角形）
  2. 遍历每个多边形的每个像素点
  3. 如果这点比屏幕上该点更浅（z比深度缓冲器更小）
    1. 更新颜色（帧缓冲器）和深度
复杂度

n个三角形复杂度为O(n)

问题
  1. 在线性时间内完成n个三角形的排序？
  2. 如果以不同顺序光栅化场景中的三角形，对结果是否由影响

着色

Bling-Phong反射模型

组成部分：名称、示意图、视觉效果、公式

着色计算与观察方向

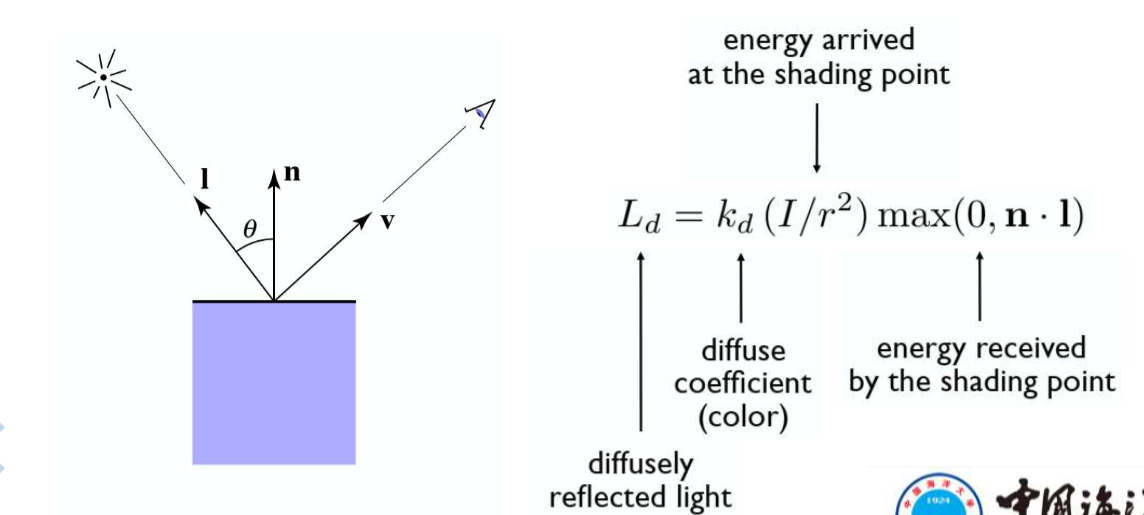
image-20260123192034401 $$L = L_a +L_d + L_s\\= k_aI_a + k_d(\frac{I}{r^2})max(0, \vec{n} \cdot \vec{l})~+~ k_s(\frac{I}{r^2})max(0, \vec{n} \cdot \vec{h})$$

漫反射

光沿各个方向均匀散射

兰伯特余弦定理

描述了有多少光/能量被接收到

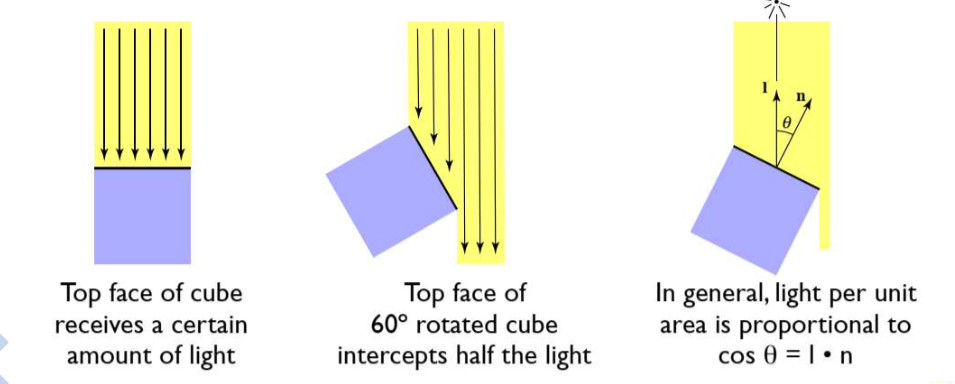
image-20260122225843271

着色与观察方向无关。主要表示物体接收到了多少光。

image-20260122230718456

镜面高光

越接近反射方向越明亮

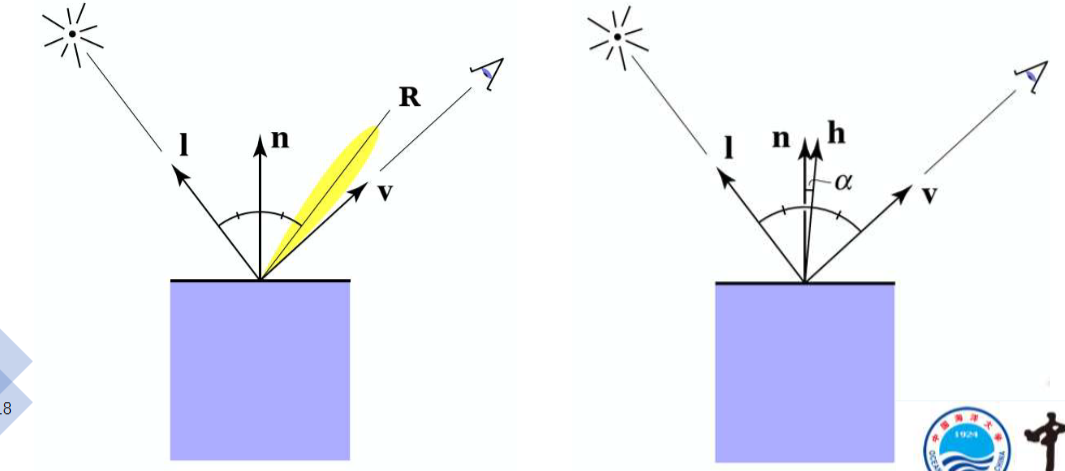
image-20260122230938818

半程向量

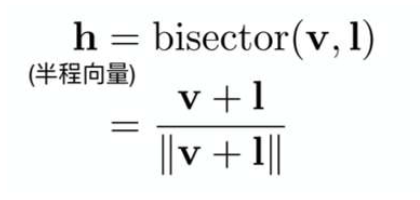
image-20260122231049263

公式

image-20260122231112400

环境光

不取决于任何其他因素

着色频率

面、顶点、像素：名称

法向量计算

面着色（Flat shading）

image-20260122231324437

三角形是平面的，得到一个面的法向量。

不适合光滑的表面

顶点着色（Gouraud shading）

三角形的顶点携带颜色信息

每一个顶点上有一个法向量

顶点法向量的计算

最好是从想要表示的集合体获取顶点法向量

否则，需要从三角形面获取顶点法向量（利用环绕顶点的面法向量取平均）

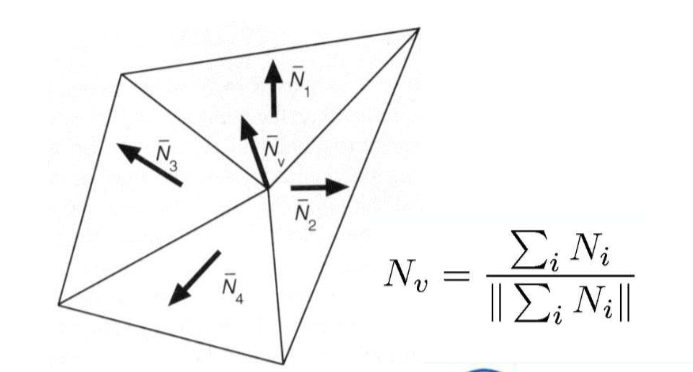
image-20260122231804122

像素着色（Phong shading）

插值得到法向量

在每个像素上计算着色模型

与Blinn-Phong反射模型区别开

像素法向量的计算

利用顶点法向量的中心插值得到（注意插值结果的归一化）

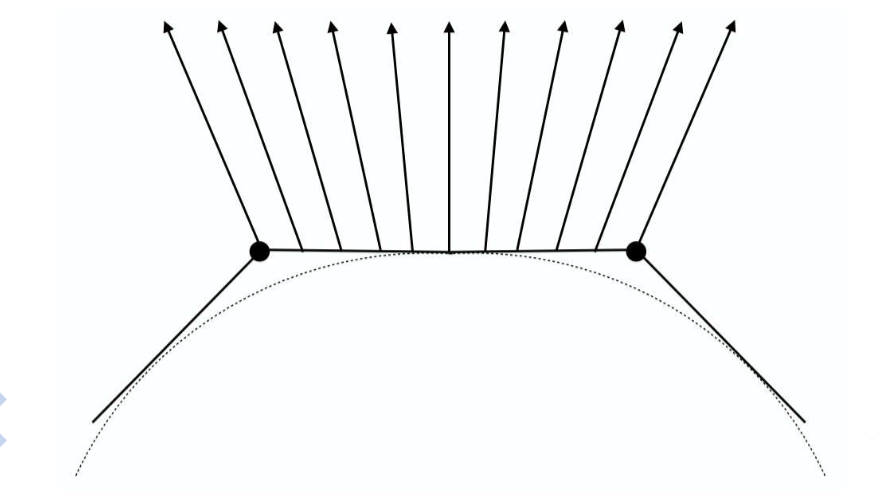
image-20260122231848842

纹理

纹理映射

三维空间中（模型）的表面上的一点总可以对应于二维图像（纹理）上的一点

每一个三角形顶点都分配有一个纹理坐标（u，v），三角形内部任一点的纹理坐标通过插值得到

插值的内容：纹理坐标、颜色、法向量

如何插值：重心坐标

重心坐标

分面积法求重心坐标

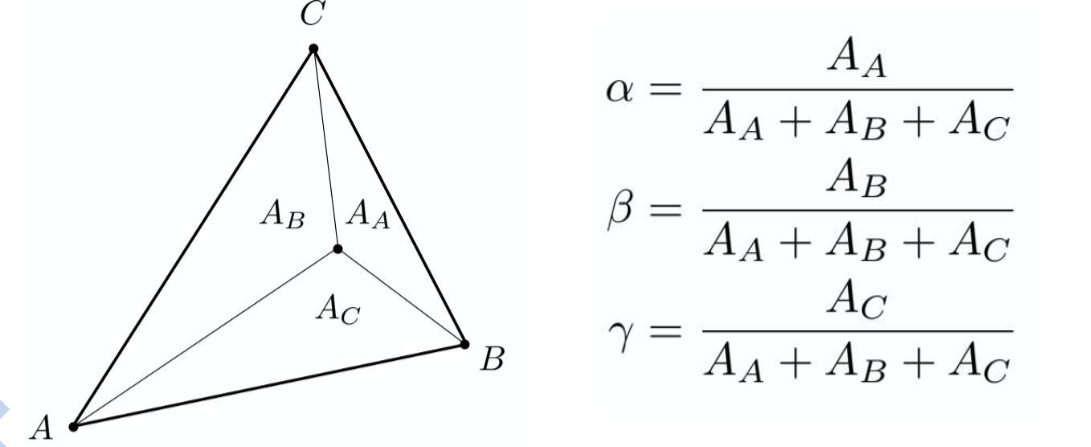
image-20260123100811910

注意到：α + β + γ = 1

计算

\[P = \alpha A + \beta B + \gamma C\\ \alpha + \beta + \gamma = 1 \implies \gamma = 1 - \alpha - \beta \]

代入消去 \(\gamma\)：

\[P = \alpha A + \beta B + (1 - \alpha - \beta)C \\P - C = \alpha(A - C) + \beta(B - C) \]

方程组变为：

\[\begin{cases} \alpha (x_A - x_C) + \beta (x_B - x_C) = x - x_C \\ \alpha (y_A - y_C) + \beta (y_B - y_C) = y - y_C \end{cases} \]

写成矩阵形式 \(M \mathbf{x} = \mathbf{b}\)：

\[\begin{bmatrix} x_A - x_C & x_B - x_C \\ y_A - y_C & y_B - y_C \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = \begin{bmatrix} x - x_C \\ y - y_C \end{bmatrix} \]

最后应用克莱姆法则得到 α 和 β

纹理应用的问题

方法、性质、异同、不足

纹理过小问题——纹理分辨率过小

如果纹理很小（分辨率不足），会出现不清晰的问题

纹理上的一个像素称为纹素。这个时候就一个纹理覆盖多个像素

解决方法：纹理放大（进行上采样）
最近邻方法

找最近的一个像素中心

双线性插值

找最近四个像素重心，进行三次线性插值。很简单

Bicubic

找邻近的16个像素中心

纹理过大问题——纹理分辨率过大

纹理很大，也就是说一个像素内对应多个纹理坐标，会产生走样问题（锯齿、摩尔纹）

也就是说纹理频率高，但是屏幕采样率低，导致高频信息丢失。

解决方法1：纹理缩小（对纹理进行下采样）
解决方法2：超采样（提高屏幕的采样率）
解决方法3：范围查询（提前过滤纹理的高频信息）
多级贴图：快速。近似，正方形范围查询

存在问题：

①log2 D 计算出的不是整数，不太平滑：使用三线性插值，两层的结果加权

②正方形受限：使用各向异性过滤或者EWA过滤

纹理应用

环境贴图：只影响着色

环境贴图包括：球形贴图和立方体贴图。

以下两种贴图在影响颜色的同时，纹理存储了高度/法线信息，用于伪造详细的几何形状

凹凸贴图

方法

添加表面细节但不改变任何几何信息（不会增加三角形的数目）

  • 在每个像素上扰动表面法线
  • 利用纹理定义每个纹素上的“高度偏移”
    • 改变法向量的过程：
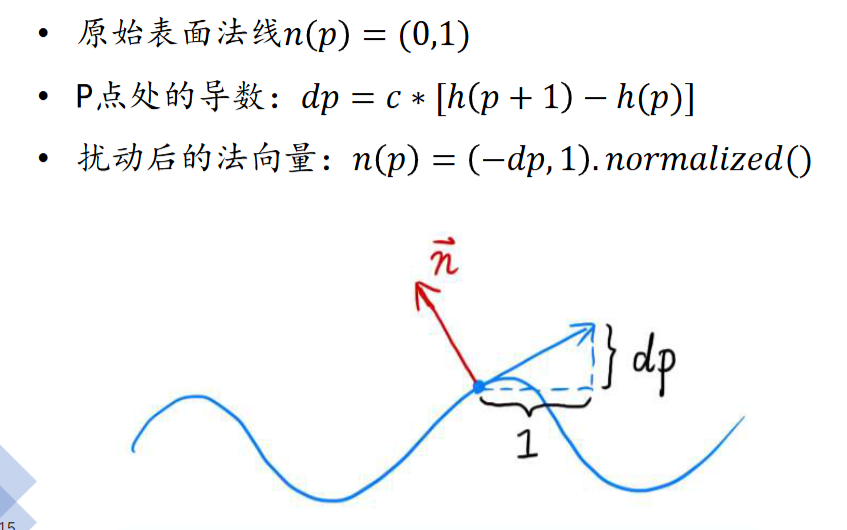
image-20260123105904823
问题
  • 在模型边缘不能很好的模拟凹凸效果
  • 阴影效果还是由真实的几何信息计算而出
image-20260123110354709

位移贴图

区别相对于位移贴图真正移动了三角形的顶点

问题
  • 对三角形数目的要求
  • 可以利用动态曲面细分来解决

几何表示

几何的表示形式

隐式

优点

  • 内外测试简单
  • 描述简洁
  • 适合做光面与表面的求交
  • 对于简单形状，描述准确，不存在采样误差
  • 易于处理拓扑结构

缺点

  • 采样困难
  • 复杂形状建模困难

例子

代数曲面、水平集、距离函数、构造实体几何、分形

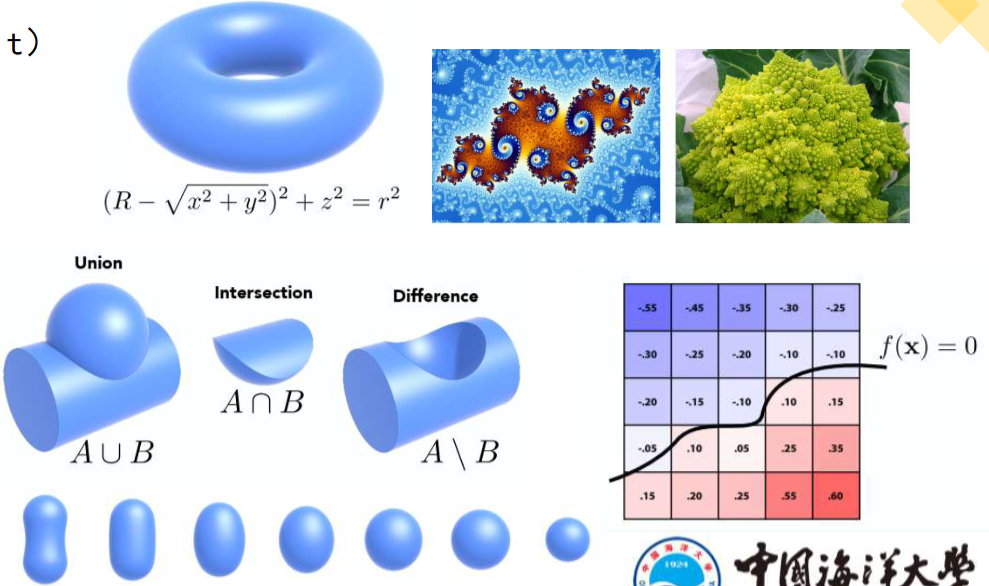
image-20260123111616879

显式

优点

采样简单

缺点

内外测试困难

例子

点云、多边形网格、细分、NURBS、OBJ文件、贝塞尔曲线

image-20260123111745673

贝塞尔曲线

公式、性质、优缺点、计算

de Casteljau算法：二次&三次

分段Bezier曲线连续性判断

基本概念

公式

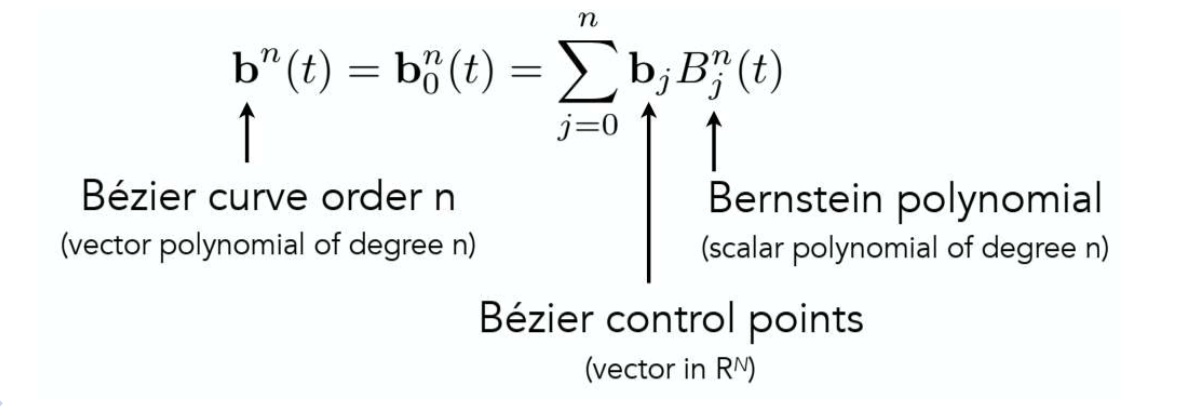
image-20260123120721802

性质

  • 仿射变换性质
    • 通过变换控制带你达到变换曲线的目的
  • 凸包性质
    • 曲线位于控制点的凸包内

优点

  • 形状控制直观，设计灵活，应用较为广泛

缺点

  • 控制顶点数较多时，多边形对曲线的控制能力较弱
  • 控制顶点数增多时，生成曲线的阶数也增高
  • 曲线拼接需要附加条件，不太灵活
  • 局部控制能力弱：因为贝塞尔基函数的值在（0，1）开区间内均不为0，曲线上任意一点都是所有给定顶点的加权平均
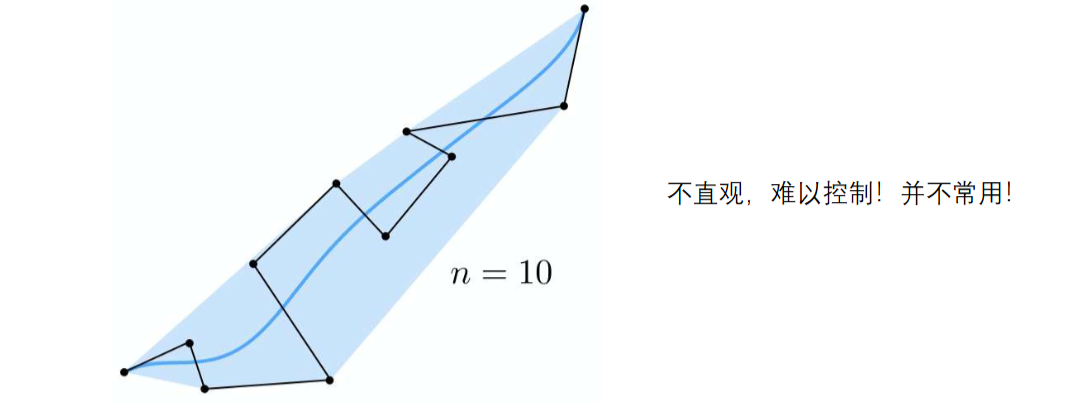
image-20260123124439155

二次贝塞尔曲线

考虑三个控制点，求t时刻对应的点

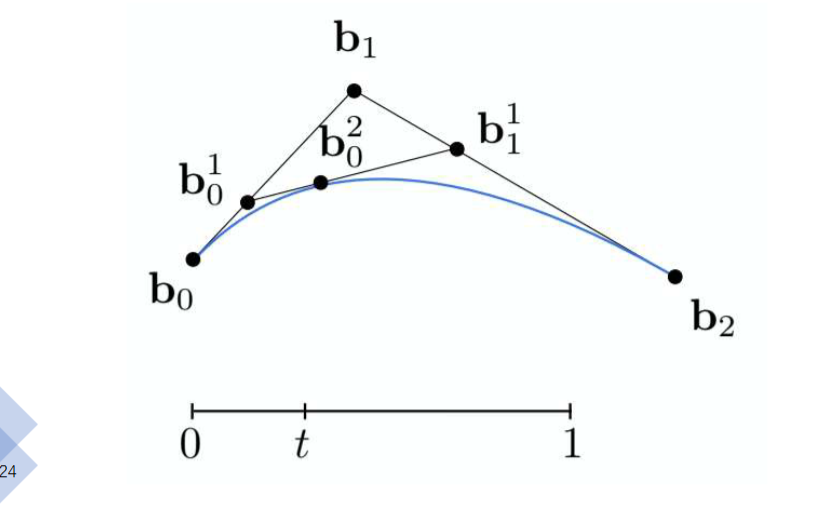
image-20260123115804298

我们进行了三次线性插值。

\[b_0^1 = t \cdot b_1 + (1-t) \cdot b_0 \\b_1^2 = t \cdot b_2 + (1-t)\cdot b_1\\b_0^2 = t \cdot b_0^1 + (i-t) \cdot b_1^2 \]

我们最终得到公式

\[b_0^2(t) = (1-t)^2b_0 + 2t(1-t)b_1 + t^2b_2 \]

三次贝塞尔曲线

考虑四个控制点

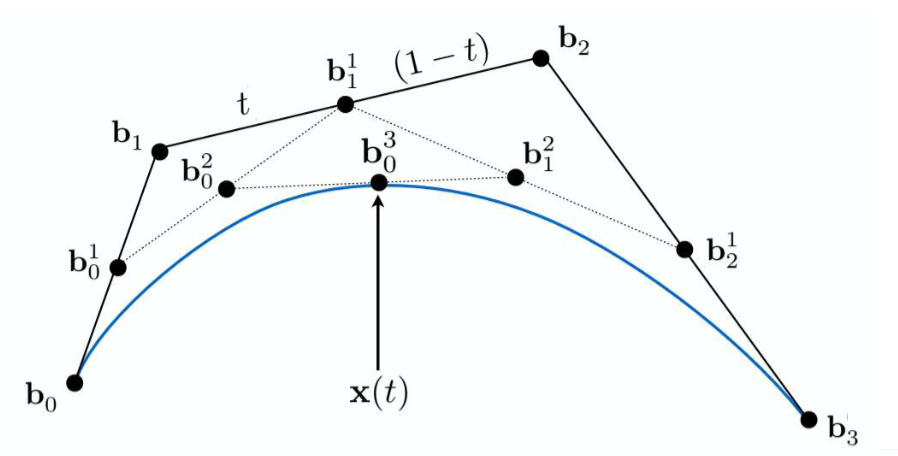
image-20260123120245163

进行六次线性插值

分段贝塞尔曲线的连续性

C0连续性

结尾和开头的值相同

\[a_n = b_0 \]

C1连续性

考虑接点处斜率相同

\[a_n = b_0 = \frac{1}{2}(a_{n-1}+b_1) \]

例题

image-20260123114825231

image-20260123165835280

几何处理

几何处理的常见任务

  • 重建：给定几何样本、重建表面

  • 上采样：通过插值提高分辨率（纹理放大、网格细分）

  • 下采样：降低分辨率，同时保持几何体的形状（纹理缩小）

  • 重采样：修改样本分布以提高质量。对于图像没这个问题，但是对于网格来说多边形的形状十分重要

  • 过滤：消除噪声或者强调重要特征

  • 形状分析：识别/理解重要的语义特征

网格细分

网格细分：Loop细分，CatMull-Clark细分（如何加点，适用范围及原因）

Loop细分

  • 针对三角形网格的常用细分方法
方法①：将一个三角形一分为四
image-20260123131537848
方法②：根据不同权重分配顶点位置

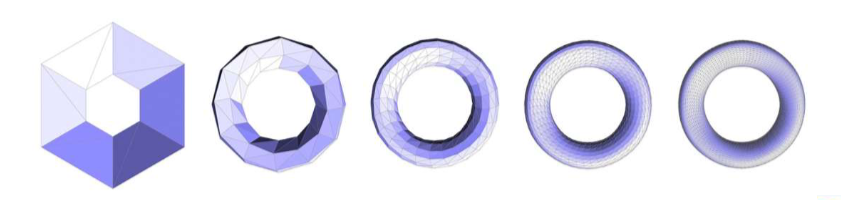
image-20260123131545737

  • 对于新顶点（重心插值）
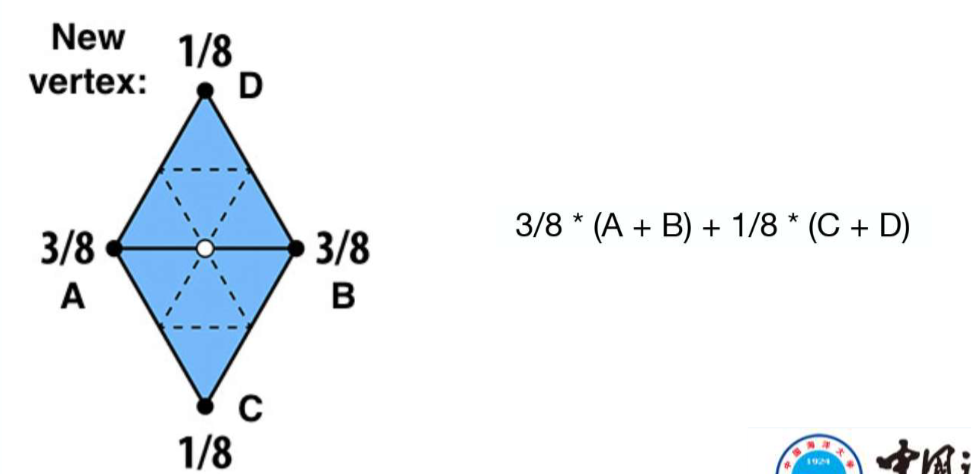
image-20260123131702656
  • 对于旧顶点

我先略。有点复杂

方法③：通过边操作进行Loop细分
  1. 以任意顺序分割原始网格的边
image-20260123132109303
  1. 反转接触新旧顶点的新边
image-20260123132149418
  1. 最后更新顶点位置

CatMull-Clark细分

  • 针对多边形网格，多用于四边形网格

方法

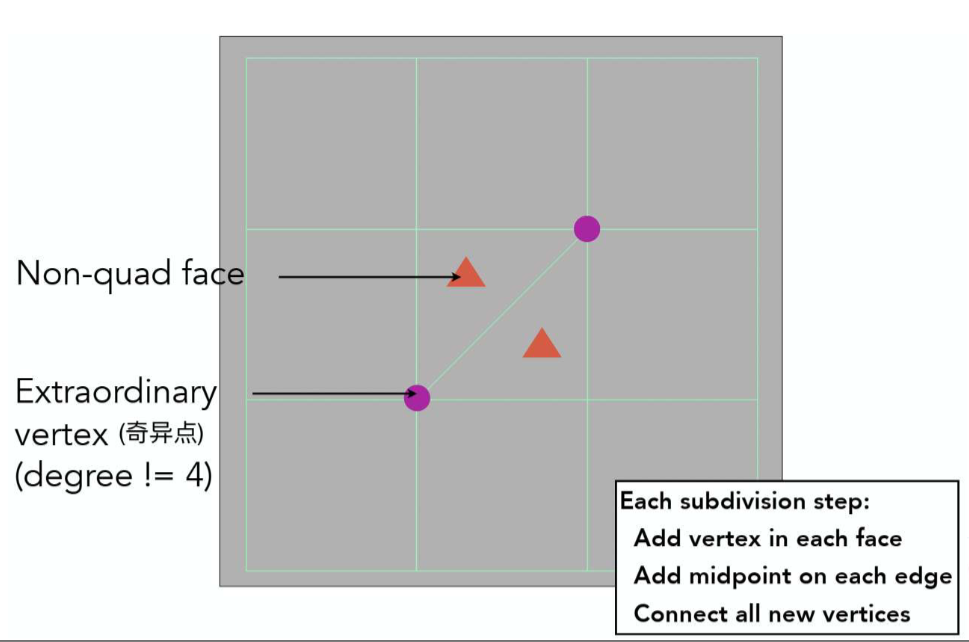
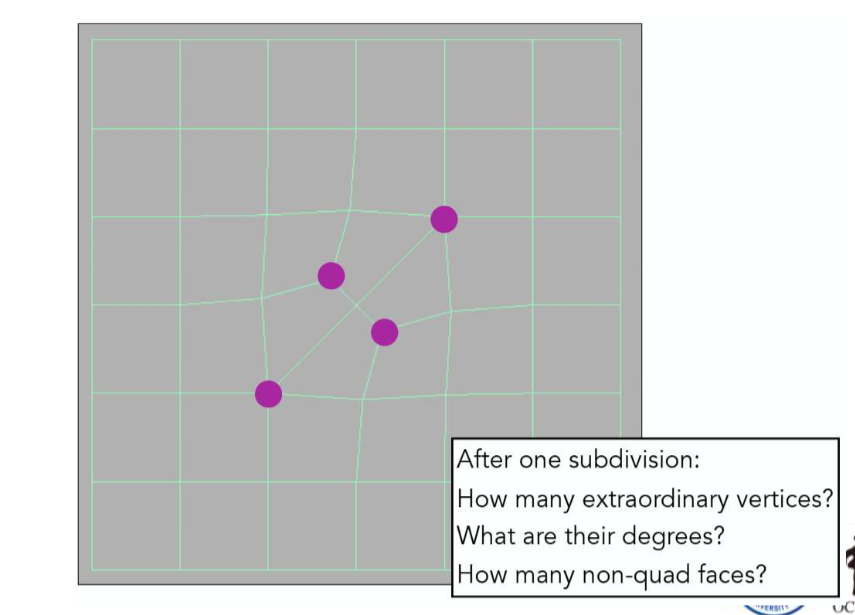
image-20260123134504144 image-20260123134518071

  1. 找奇异点（degree != 4）

  2. 添加面点

    • 取面内所有原始顶点的平均值，找到面心

  3. 添加边点

    • 边点 = （a+b+c+d）/ 4，其中a、b是边的两个端点；c、d是相邻两个面的面点

  4. 连接新顶点

光线追踪

光线投射算法

  1. 从视点或像素出发，仅对穿过像素的光线反向跟踪
  2. 当光线路径到达一个离视点最近的可见的不透明物体的表面时，停止追踪
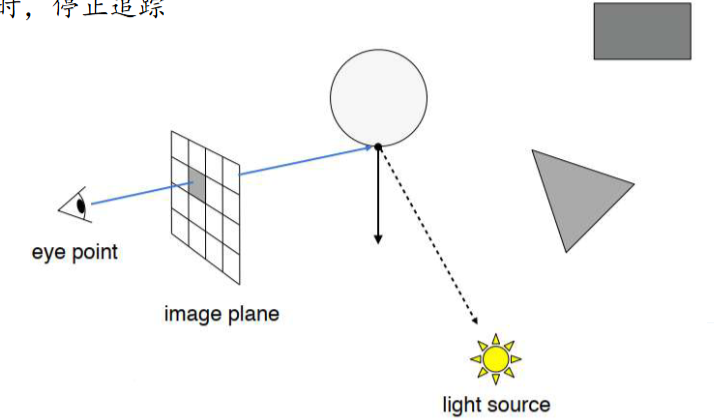
image-20260123155819918

Whitted-Style光线追踪算法

光线投射算法中：被追踪的光线仅从每个像素到离他最近的景物为止

光线追踪算法中：追踪多条光线在场景中的路径，以得到多个景物表面所产生的反射和折射影响

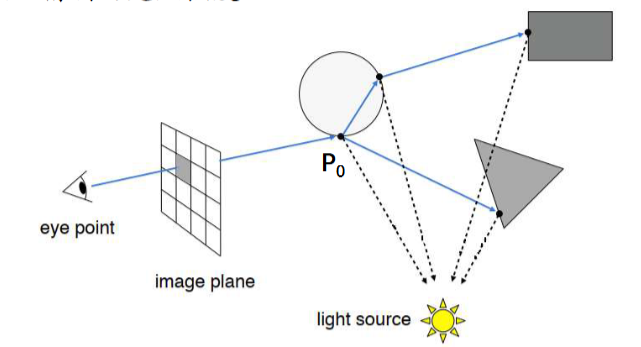
image-20260123161015874

方法

  1. 沿着到达视点的光线的相反方向追踪
  2. 经过屏幕上一像素点找出与视线所交的物体表面点P0
  3. 继续追踪，找出影响P0点光强的所有的光源
  4. 算出P0点上精确的光照强度

结束条件

  • 光线与光源相交
  • 光线与漫反射表面相交
  • 被追踪给的光线对第一个交点处的贡献趋近于0

光线与三角网格求交

动机

  • 渲染：可见性、阴影、光照的计算
  • 几何：内部/外部测试

Moller Trumbore算法

光线与包围盒求交

二维

  1. 分别计算光线与两对平行线的交点
  2. 求线段的交集，确定最后结果
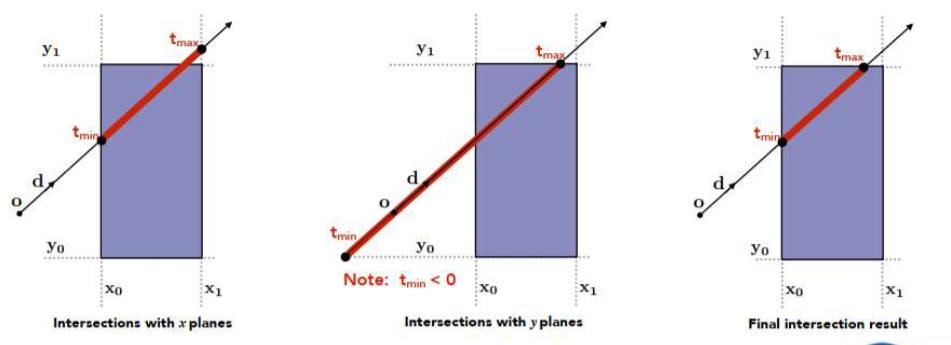
image-20260123161436852

三维——光线与轴对齐包围盒求交

  • 仅当光线进入所有成对平板时，光线进入到包围盒内
  • 光线离开任意一对平板时，即离开了包围盒
  1. 对每一对平板，计算 \(t_{min}\) 和 \(t_{max}\)
  2. 对包围盒， \(t_{enter}\) = \(max(t_{min})\) , \(t_{exit}\) = \(min(t_{max})\) （最晚进去的，最早出来的）
有交点的情况

\[t_{enter} < t_{exit} 并且 t_{exit} \ge 0 \]

利用AABB加速光线追踪

均匀空间划分（Grid）

算法
  • 确定包围盒
  • 构建均匀网格
  • 将物体存储在与物体重叠的相应网格中
  • 按照光线穿过的方向逐步地遍历网格；对于每一个网格，测试光线与该网格中存储的所有对象的交集

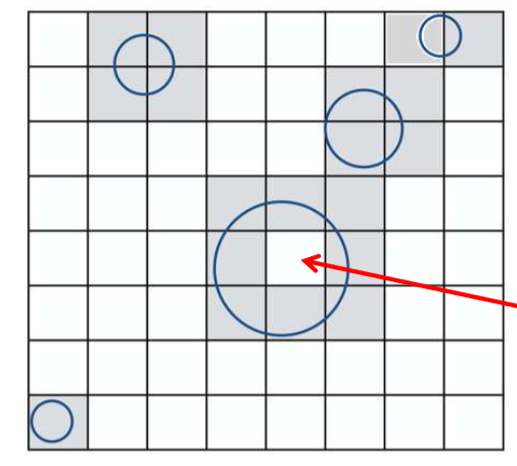
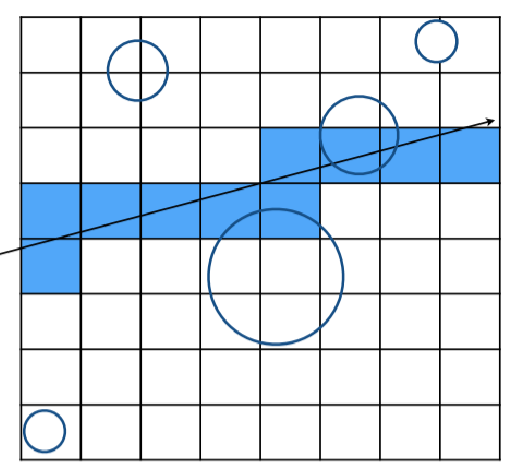
image-20260123165433423image-20260123165555685

适用场景：空间中存在大量物体，并且它们的大小和空间分布都比较均匀

不适用场景：“运动场中的茶壶”

空间划分（KD-Tree）

把空间划分成不重叠的区域

空间中的一个物体可能包含在不同的区域中

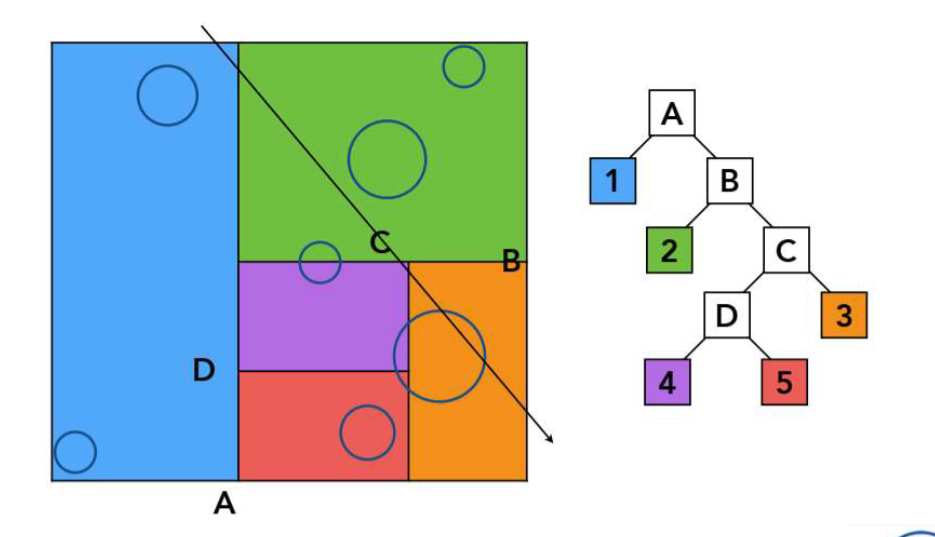
image-20260123165647805

物体划分（层次包围盒BVH）

把物体几何划分成不相交的子集

包含每个子集的包围盒在空间中可能存在重叠

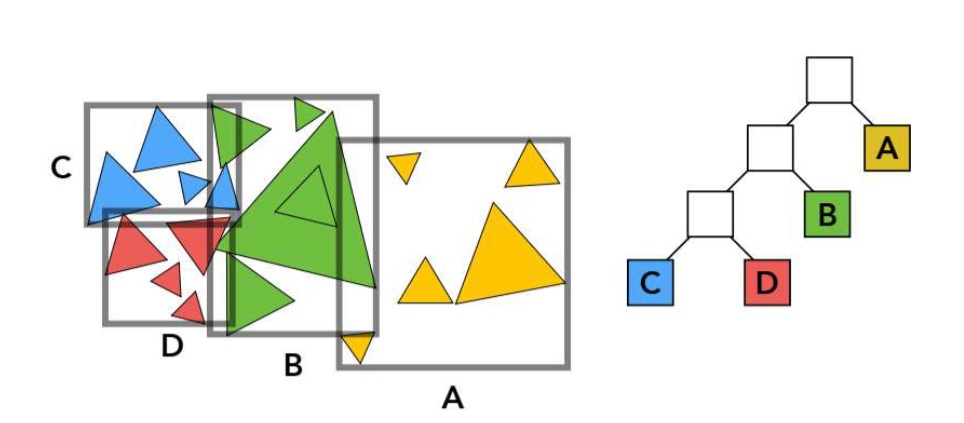
image-20260123165715122

路径追踪

Whitted Ray Tracing仅处理镜面反射和折射，而路径追踪的反射类型包括漫反射。

直接光照

向光源采样，无需RR

间接光照

半球随机采样，必须RR

  1. 从摄像机通过像素发射一条光线
  2. 找到光线与物体的交点 p
  3. 在 p 的半球面上 随机选择一个方向 发射下一条光线
  4. 为了防止光线无线弹射，引入俄罗斯轮盘赌。以概率P继续弹射，以 1-P停止并返回

动画与模拟

计算机动画的基本技术（概念、利弊）

正向运动学

动画师提供角度，计算机确定末端位置p

动画被描述为关于时间的角度参数值的函数

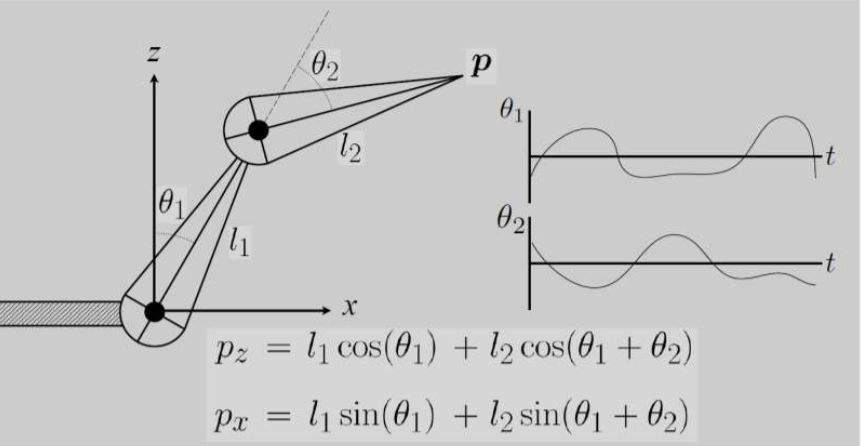
优点

  • 直接控制，非常方便
  • 很直观，容易实现

缺点

  • 动画可能与物理规律不一致
  • 艺术家需要耗费大量时间

逆向运动学

动画师提供末端位置p，计算机必须给出满足约束条件的关节角度

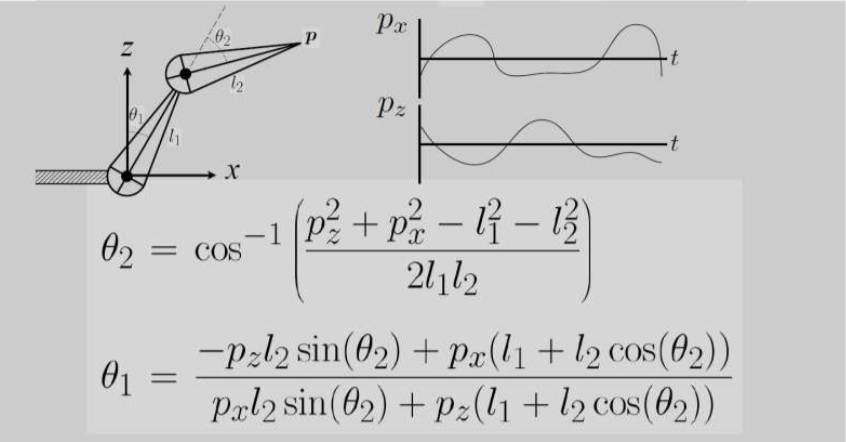
image-20260123183944803

缺点

  • 可能无解或有多个解

动画绑定

动画绑定是一组更高级别的对动画角色的控制操作，允许更快速和直观的修改姿势、变形、表情等。

缺点

  • 应用起来代价高
    • 人力成本高
    • 对艺术造诣和技术能力都有较高要求。我只能说确实

动作捕捉

动画捕捉是利用数据驱动的方式来创建动画序列。包括记录真实世界中人的行为，从收集到的数据中提取姿态，生成关于时间的函数

优点

  • 能够快速捕获大量真实数据
  • 生成的动画真实度高

缺点

  • 需要复杂和昂贵的前期配置
  • 捕获的动画可能不符合艺术需求，还需要后期修改

PPT上的题目

image-20260123185101946 image-20260123185134391 image-20260123185201481 image-20260123185210240 image-20260123185313133 image-20260123185351231 image-20260123185433957 image-20260123185451458 image-20260123185528282 image-20260123185908897
posted @ 2026-01-23 19:47  Pocon  阅读(18)  评论(0)    收藏  举报