中国海洋大学2023离散数学Ⅱ复习总大纲

图片需要挂梯子

第七章图

会求图中顶点的度、邻域、关联集，图的周长、围长

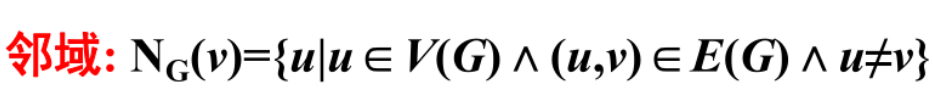
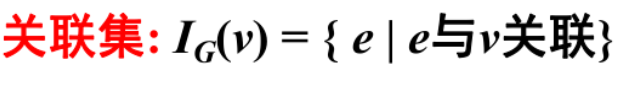
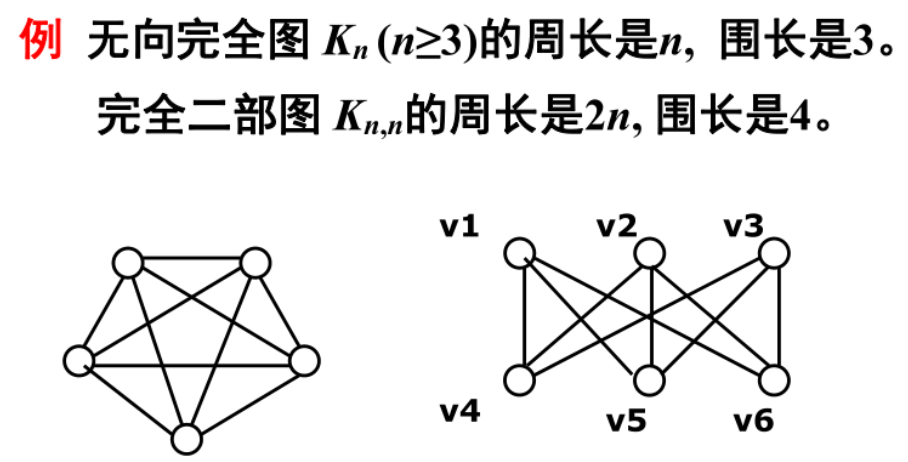
周长：最长圈的长度

围长：最短圈的长度

距离：u、v间短程线的长度（ d(u, v) ）

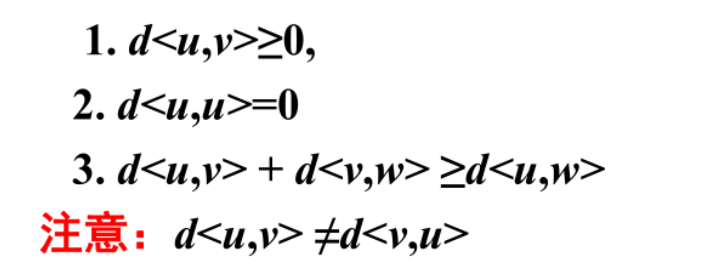
直径：两点间的最长距离（ d(G)= max{ d(u,v) } ）

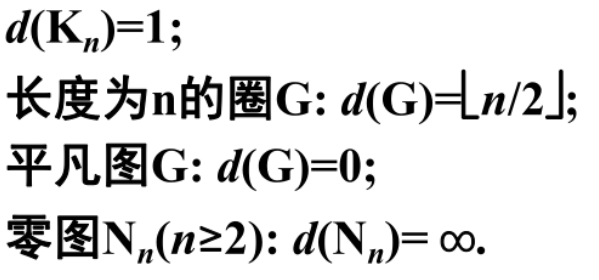
熟练掌握和应用（有向图、无向图）的握手定理

定理1：每个图中，顶点度数的总和等于边数的两倍

定理2：度数和等于边数乘2。有向图中入度和和出度和相同。

推论：在任何图中，奇数度顶点的个数是偶数

例题

理解简单图、零图、k-正则图、补图的概念

简单图：无环、无平行边

k-正则图：每个点的度数都是k。（利用握手定理求边数）

n阶完全图：n阶简单图

补图：点不变，边相补

自补图：具有 n 个顶点的自补图的个数为 2 个，n 满足 mod 4 = 0， 1

基图：有向图去掉方向

判定正整数列可否简单图画，并能至少给出两个不同构的图

判断是否可图化
1. 最大度是否小于点的个数
2. 是否满足握手定理（偶数个奇数度顶点）
判断是否可简单图化
Havel定理：把d排序后，找出度最大的点（设度为d1），把它与度次大的d1个点之间连边，然后这个点就可以不管了，一直继续这个过程，直到建出完整的图，或出现负度等明显不合理的情况。

同构图：两个图中的节点和边存在一一对应，且保持关联关系

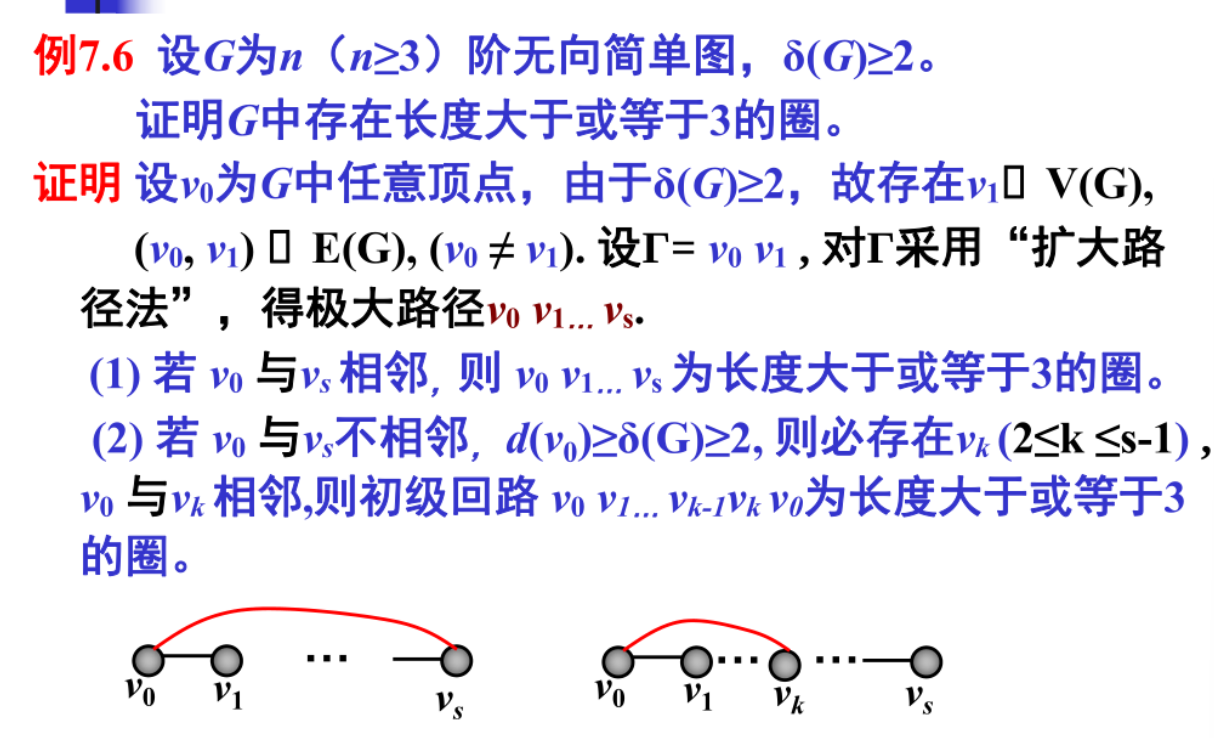
掌握极大路径及其相关习题和例题

熟练求出点连通度κ，边连通度λ；有向图的三种连通

点连通度：若破坏连通性，至少要删除多少个顶点
点割集

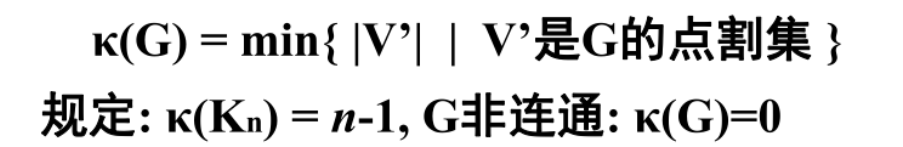
边连通度：若破坏连通性，至少要删除多少条边
边割集

3阶以上无向简单连通图G是2-连通图

<=> G中任意两个顶点之间有两条以上独立路径

<=> G中任意两个顶点共简单回路

<=> G中任意两个顶点之间有两条以上边不交路径

强连通：存在至少包含每个结点一次的回路

强分图（具有强连通性质的最大子图）——有向图的每一个结点位于仅且一个强分图中

强连通图的基图没有割边

单向连通：存在经过每个顶点至少一次的路

单侧分图（具有单侧连通性质的最大子图）

单向连通的基图一定是连通的

弱连通：不满足以上条件，但只有一个连通分支=>弱分图

掌握Whitney定理（κ，λ，δ三者之间的关系）

定理7.10 （Whitney定理）

\[\kappa \le \lambda \le \delta \]

推论：k -连通图一定是k-边连通图

定理7.11

n阶简单连通图的κ，λ，δ之间关系有且仅有3种可能

理解割点、桥

v是割点<=>{v}是割集<=>可以将图划分为2块，两块中点的任意路径都要经过该点

(u,v)是桥<=>{(u, v)}是边割集<=>可以将图划分为两块，两块中点的任意路径都要经过该边

掌握二部图的定义及判定定理（定理7.8），完全二部图的定义和性质

判定定理7.8：一个无向图是二部图当且仅当图中无奇圈

完全二部图是一种特殊的二分图，两部分中所有顶点都相连。

拉姆齐问题

建模
认识是原图、不认识是补图
运用鸽巢原理

重点课后习题

建模
度数1~n-1，人数1~n
鸽巢原理

第八章欧拉图与哈密顿图要点

掌握（半）欧拉图和（半）哈密顿图的定义

欧拉图定义

欧拉通路：经过图中所有边的简单通路

欧拉回路：经过图中所有边的简单回路

欧拉图：有欧拉回路的图

半欧拉图：非欧拉图，有欧拉通路

哈密顿图定义

哈密顿通路：经过图中所有顶点的初级通路（点不重）

哈密顿回路：经过图中所有顶点的初级回路

哈密顿图：有哈密顿回路的图

半哈密顿图：有哈密顿通路的图

能够判断是否是欧拉图（定理8.1-8.4）

定理8.1

G是欧拉图

<=> G中所有顶点都是偶数度

<=> G是若干个边不交的圈的并

定理8.2

G是半欧拉图

<=> G中恰有2个奇度顶点

定理8.3

G是有向欧拉图

<=>

<=> G是若干个边不交的有向圈的并

定理8.4

G是有向半欧拉图

<=> G中恰有2个奇度顶点，其中一个入度比出度大1，另一个出度比入度大1，其余顶点入度等于出度

能够判定是否是哈密顿图，即掌握哈密顿图的充分条件和必要条件（定理8.6及推论，定理8.7及推论）

定理8.6(无向哈密顿图的必要条件)

设G = <V, E>是无向哈密顿图，则对V的任意非空真子集V1，

\[P(G-V_1) \leqslant |V_1| \]

即删除这些顶点后剩下的连通分支数是否小于删除的点的数量

所以有割点或桥，就不是哈密顿图

此定理经常被用来判定图是非哈密顿图（分支数如果比删的点多就不是）

定理8.6推论（无向半哈密顿图的必要条件）

设G = <V, E>是无向哈密顿图，则对V的任意非空真子集V1，

\[P(G-V_1) \leqslant |V_1|+1 \]

定理8.7（哈密顿通路的充分条件）

若G是n（≥2）阶无向简单图，若对G中任意不相邻顶点u与v有

\[d(u) + d(v) \geqslant n-1 \]

则G存在哈密顿通路

定理8.7的推论1（哈密顿回路的充分条件1）

设G是n（≥3）阶无向简单图，若对G中任意不相邻顶点u与v有

\[d(u) + d(v) \geqslant n \]

则G是哈密顿图

定理8.7的推论1（哈密顿回路的充分条件2）

设G是n（≥3）阶无向简单图，若对G中任意顶点u有

\[d(u) \geqslant \frac{n}{2} \]

则G是哈密顿图

能够给出欧拉回路和哈密顿回路

例题

利用度数都为偶数可以做

哈密顿图的判定定理。利用反证法

看似是匹配问题，实际上是哈密顿回路

建模
满足哈密顿通路的充分条件
下结论

如K4

没说连通性

第九章树要点

掌握树的6个等价定义

G是树（连通无回路）

<=> G中任二顶点之间存在唯一路径

<=> G中无圈且m=n-1

<=> G连通且m=n-1 （点，边，度数和，知一求三）

<=> G连通且每条边均为桥

<=> G无圈，但在任二不同顶点之间增加新边，所得图含唯一的一个圈

这里可以和握手定理一起考察

定理9.2：任一n阶非平凡无向树至少有两片树叶

掌握生成树的概念

生成树T：T是G的生成子图，且T为树（点不变，边在原图中选）

树枝：生成树上的边

弦：原图中的边且不是生成树上的边

余树（或补）：原图减去生成树

余树不一定是树

6阶无向简单图G，边数为5，T的补有两种情况

T的补是生成树
T的补不连通且含圈

生成树的存在定理（定理9.3）

定理9.3：无向图具有生成树当且仅当G是连通的

T是G的生成子图。 T的阶是n。 T的边数是n-1

推论1：设G为n阶m条边的无向连通图，则m≥n-1

推论2：设T为n阶m条边的无向连通图G的一棵生成树，则T的余树中含m-n+1条边

推论3：设T是连通图G中一棵生成树，C为G中任意一圈。则余树和圈C必有交集

能求出图的生成树，掌握生成树的不同求法（破圈法。定理9.6，利用基本关联矩阵求生成树即定理10.3）

破圈法：若图中无圈，则图本身就是生成树。否则删去圈上的任一条边，这不破坏连通性。重复进行直到无圈为止，剩下的图是一棵生成树。

定理9.6

定理9.7

\[\tau(K_n) = n^{n-2}(n \ge 2) \]

定理10.3

列出矩阵的关联矩阵
删去一个边（悬挂边也可以删去，因为所有生成树必经过这个悬挂边）
- 注意不能删除桥，如果删除桥图不连通，不存在生成树
求n-1阶子式（选n-1条边）的秩。如满秩，则选中的边合并去掉的边可以生成一棵生成树

熟练求出基本割集系统和基本回路系统、求出断集空间和环路空间、计算断集空间和环路空间的维数

环路：G中圈或若干个边不重的圈的并

圈、简单回路都是环路，但环路不一定是回路

基本回路系统：一条弦加上树枝组成的回路为基本回路，基本回路的集合为基本回路系统

故余树中的任意一条边在且仅在一个回路中

定理9.11：设G为无向连通图，T是G的任意一棵生成树，则G中任一回路或为T的基本回路或为若干个基本回路的环合

定理9.12

\[设G是n阶m条边的无向连通图，则C_环是 Ω 的m-n+1维的子空间 \]

基本割集系统：一条树枝加上弦组成的割集为基本割集，所有割集的集合为基本割集系统

故树中的一条边在且仅在一个基本割集中

割集是断集，断集不一定是割集

定理9.17

\[设G是n阶m条边的无向连通图，则S_断为Ω的n-1维子空间 \]

掌握根树的定义、根数中顶点层数的定义

根树：顶点分3类的有向树（基图是树的有向图）

顶点v的层数：L(v) = 从树根到v路径长度

树高：h(T) = 顶点的最大层数
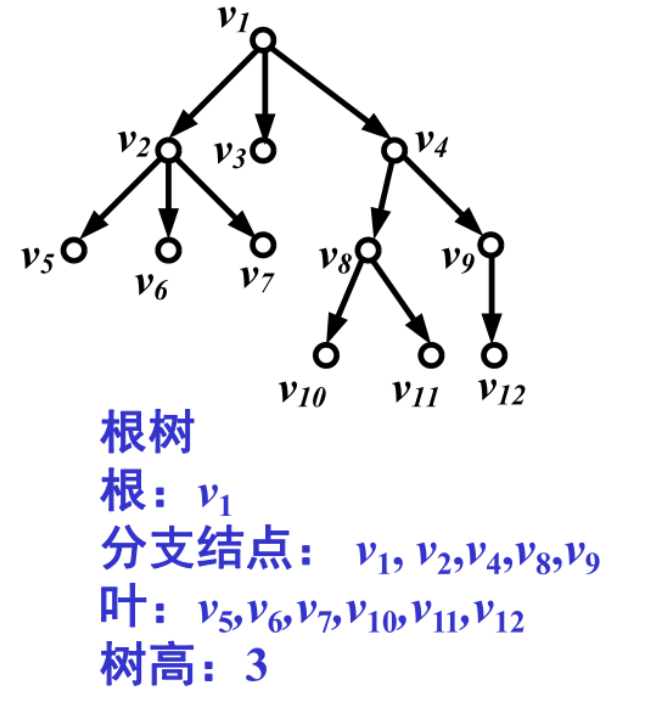根也算是分支点

r叉树、正则树、完全树的定义及定理

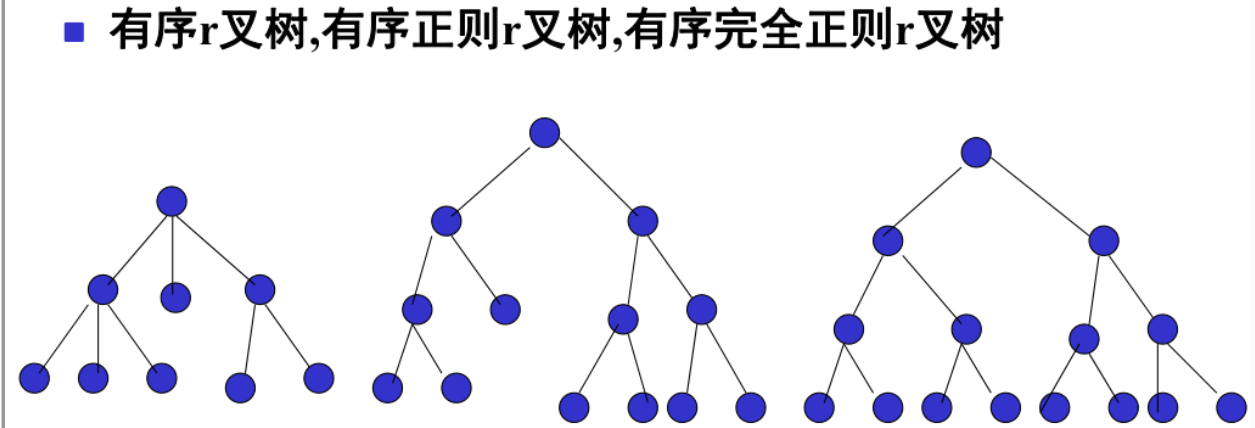
定理14.13： 设正则r（≥2）叉树T有i个分支点和t个树叶，则（r-1）i = t-1

即 m = t+i-1 = ri （出度等于入度）

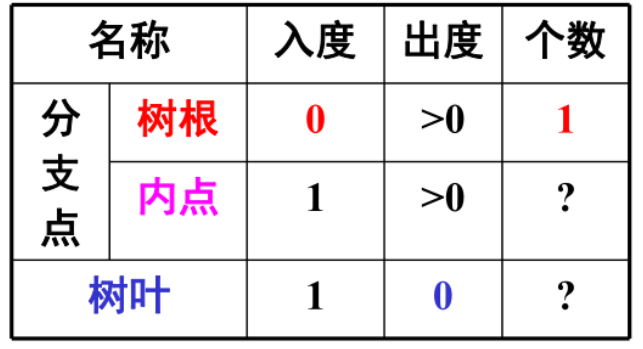
分支节点的出度均为r，树叶的出度为0。

根节点的入度是0，其他分支节点和树叶的入度是1

根子树：v是根树的一个结点且不是树根，称v及其所有后代的导出子图为以v为根的根子树

左（右）子树：2叉正则有序树每个分支点的左右两个儿子导出的根子树

前缀码

码字互相不为前缀的不等长编码

例题

正则r叉树的应用

1. 第一个接线板看作树根，每个接线板看作分支点，每盏灯作为树叶，构成正则四叉树

2. 利用定理14.13。取上界

生成树的数量（8个） kn的生成树有n^(n-2)个

计算环路空间和断集空间

应用定理14.13，和树的性质

设T为非平凡的无向树，Δ(T) ≥ k，证明至少有k片树叶

设v∈V(T)，且d(v)=△(T) ≥k（k≥1）。显然v为分支点，则它是割点。

设G'= T-v，则G'至少有k个连通分支。设T1,T2,…,Tk为G'的k个连通分支，易知它们
都是树。

若存在Ti为平凡树，则Ti具有唯一的顶点vi为T的树叶。若Tj不是平凡树，则

Tj至少有两片树叶，其中至少有一片是T的树叶，于是T至少有k片树叶。

第十章图的矩阵表示

写出给定图的（基本）关联矩阵、邻接矩阵，反之，根据关联矩阵和邻接矩阵画出图

关联矩阵：点与边的关系

无环有向图的关联矩阵：-1（边的起点），0（无关联），1（边的终点）

无环无向图的关联矩阵：1（有边向连），0（无相连）

注意关联矩阵不能表示自环

邻接矩阵：有向图点与点的关系

\[A(D) = [a_{ij}]_{n \cdot n}，a_{ij}=从v_i到v_j的边数 \]

掌握关联矩阵和邻接矩阵的性质

关联矩阵

有向图：

所有相加为0
一行的1相加为该点出度（d-），一行的-1为该点的入度（d+）

无向图：

每行和为点的度数
每列和为2

邻接矩阵

有向图：

每行和为出度
每列和为入度
主对角线为环的个数

相邻矩阵

利用基本关联矩阵求生成树，用邻接矩阵求通路及其可达矩阵P和连通矩阵

连通图的秩

用邻接矩阵求通路数

即闭包原理，利用矩阵的高次幂

可达矩阵

可达矩阵的性质

对角线都为1
强连通图所有元素都是1
对角块是连通分支的可达矩阵

第十一章平面图

理解平面图和平面嵌入的定义

可平面图：可以画在平面上，使得边与边不在非顶点处相交的图（表示图具有平面性质）

平面嵌入：将平面图画在平面上使得边于边不在非顶点处相交（平面图的一种表现形式，平面图的平面嵌入不唯一）（可平面嵌入<=>可球面嵌入）（任何平面嵌入的内部面都可以在另一种平面嵌入下成为外部面）

平面图：在平面上边于边不在非顶点处相交的图

约当曲线：自身不相交的，始点和终点重合的曲线。

约当定理：L是平面上的一跳约当曲线。平面的其余部分被分成了两个不相交的开集，分别称为L的内部和外部，则连接L的内部点和外部点的任何连续曲线必与L相交

区域：不含顶点与边的极大连通曲面，R

面：区域及其边界

面的次数：deg(R)=边界长度

悬挂边对面的次数贡献是2

外平面图：平面图的所有顶点可都在一个面的边界上

极大平面图的判定及其性质（定理11.4，参考PPT）

极大平面图：是平面图，但是在任意两个不相邻顶点之间加边就是非平面图

特点：

极大平面图一定连通
n ≥ 3 时，极大平面图不含有割点和桥

定理11.4：n（≥3）阶简单连通平面图是极大平面图 <=> ∀R，deg(R) = 3 =>不能加边而不交叉

定理11.5：n（≥4）阶极大平面图G中，δ(G) ≥ 3（区分简单平面图的定理）

极大外平面图

判定条件

性质

掌握并能应用欧拉公式（定理11.6，11.7）

欧拉公式：设G是连通平面图，则

\[\bold{n - m+r=2} \]

n是平面图的阶数，m是平面图的边数，r是平面图的面数

欧拉公式的推广：设G是平面图，则

\[\bold{n - m + r = 1 + p} \]

n是平面图的阶数，m是平面图的边数，r是平面图的面数，p是连通分支数

平面图的性质，定理11.2，定理11.8、11.9、11.10、11.11（掌握这四个定理的证明方法），定理11.12

定理11.2：

即次数和的边的数量*2（转化为握手定理，次数和即为度数和，面即为点）

边的次数*2又为点的度数和

故面的次数和 = 边*2 = 点的度数和

定理11.8：

\[\bold{设G是连通平面图，G的各面的次数至少是l(\ge3)，则m \le \frac{l}{l-2}(n-2)} \]

证明：利用欧拉定理

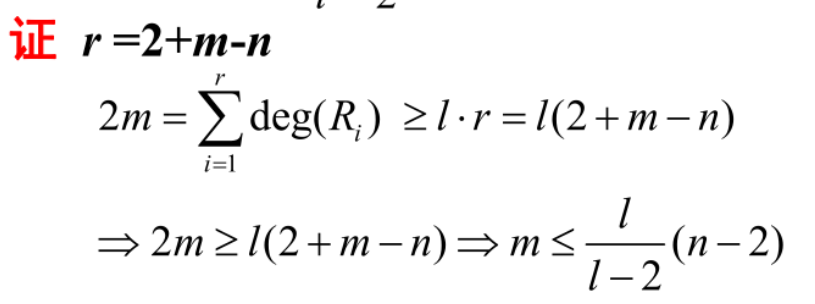
定理11.8的推论：G变为不连通，(n-2)换为(n-p-1)即可

\[\bold{设G是连通平面图，G的各面的次数至少是l(\ge3)，则m \le \frac{l}{l-2}(n-p-1)} \]

定理11.10（简单平面图性质）

\[\bold{设n(\ge 3 )阶简单平面图G有m条边，则m \le 3n-6} \]

证明：

定理11.11

\[\bold{设n(\ge 3 )阶简单极大平面图G有m条边，则m = 3n-6} \]

证明：

定理11.12

设G是简单平面图，则δ(G) ≤ 5

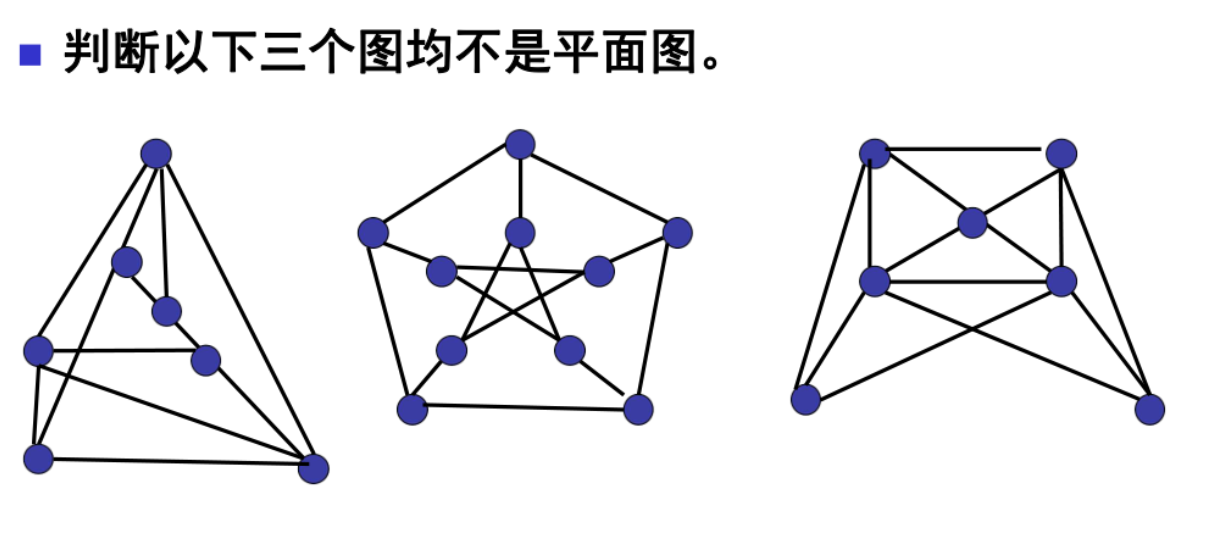
掌握并能应用平面图的判定定理 Kuratowski 定理说明给定的是否是平面图（注意复习例题）

同胚：反复插入或删除2度顶点后同构

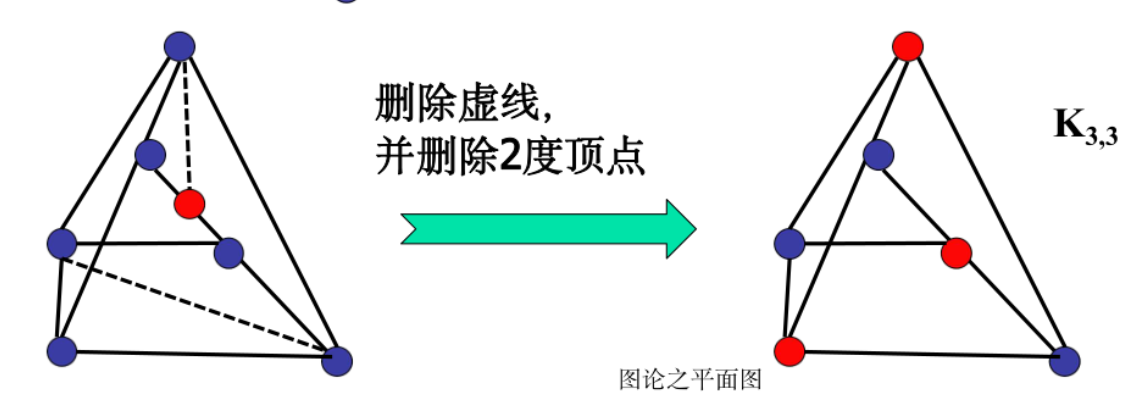
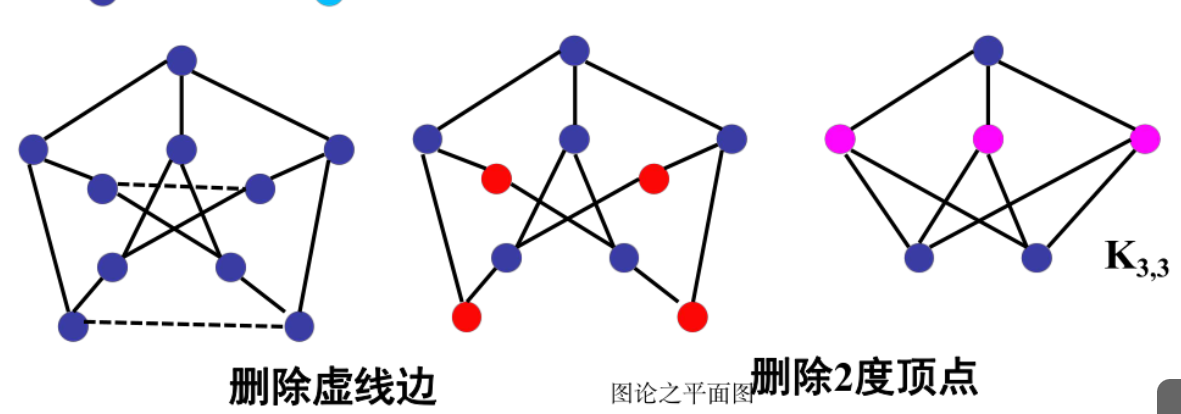
定理11.13：图G是平面图<=>G没有与K5或K3,3同胚的子图（可以删边和二度点）

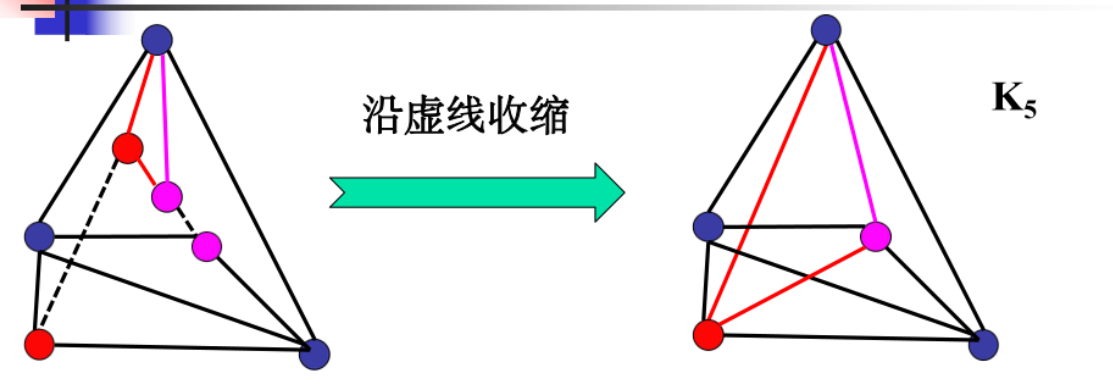
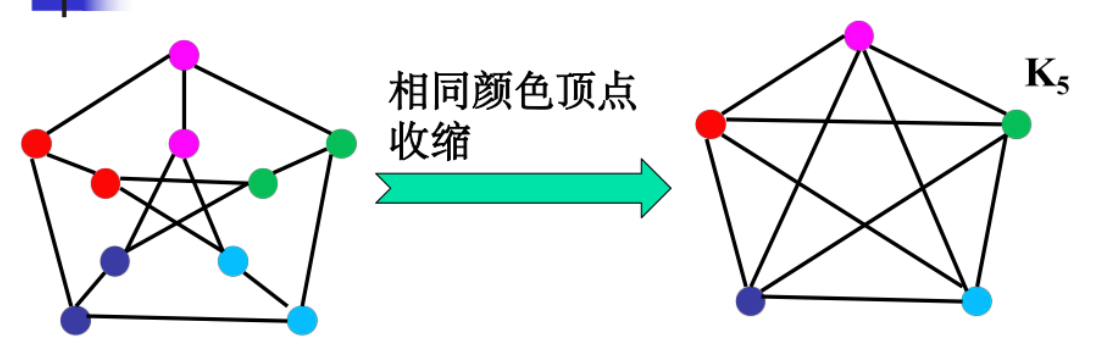
定理11.14：图G是平面图<=>G没有可以边收缩到K5或K3,3的子图

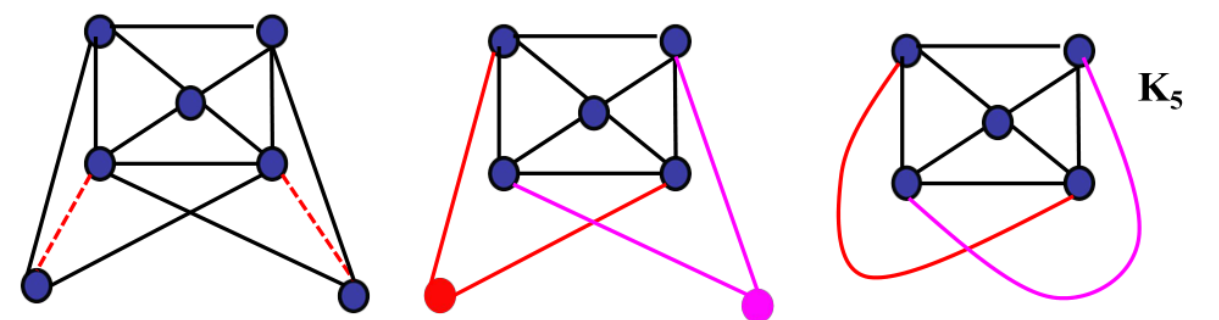
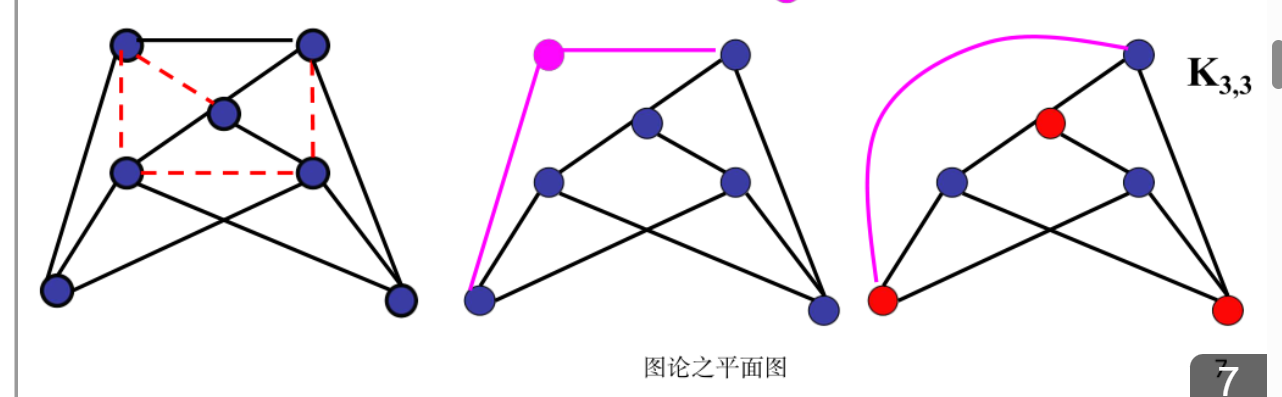
掌握对偶图的求法及其性质（定理11.15，11.16），会求对偶图的定点数n、边数m和面数r*

求法：

面（包括外部面）化为点
各面之间有几条边，各点就连几条边（悬挂边为自环）

性质：

G*是连通的
G*是平面图，也是平面嵌入
若边e是G中的环，则G*与e对应的边e*为桥

若e为桥，则G*中与e对应的边e*为环
若G的面Ri和Rj的边界上至少有两条公共边，则关联vi*和vj*的平行边。在多数情况下G*含有平行边
同构的平面图的对偶图不一定同构

定理11.15

G*是连通平面图G的对偶图，n* ,m*,r*和n.m.r分别G'和G的顶点数，边数和面数，则

n*= r （点面互换）
m* = m （边相等）
r* = n
G*的顶点vi*位于G的面Ri中，则vi*的度数和Ri面的次数相同

掌握自对偶图及其性质（参考PPT）

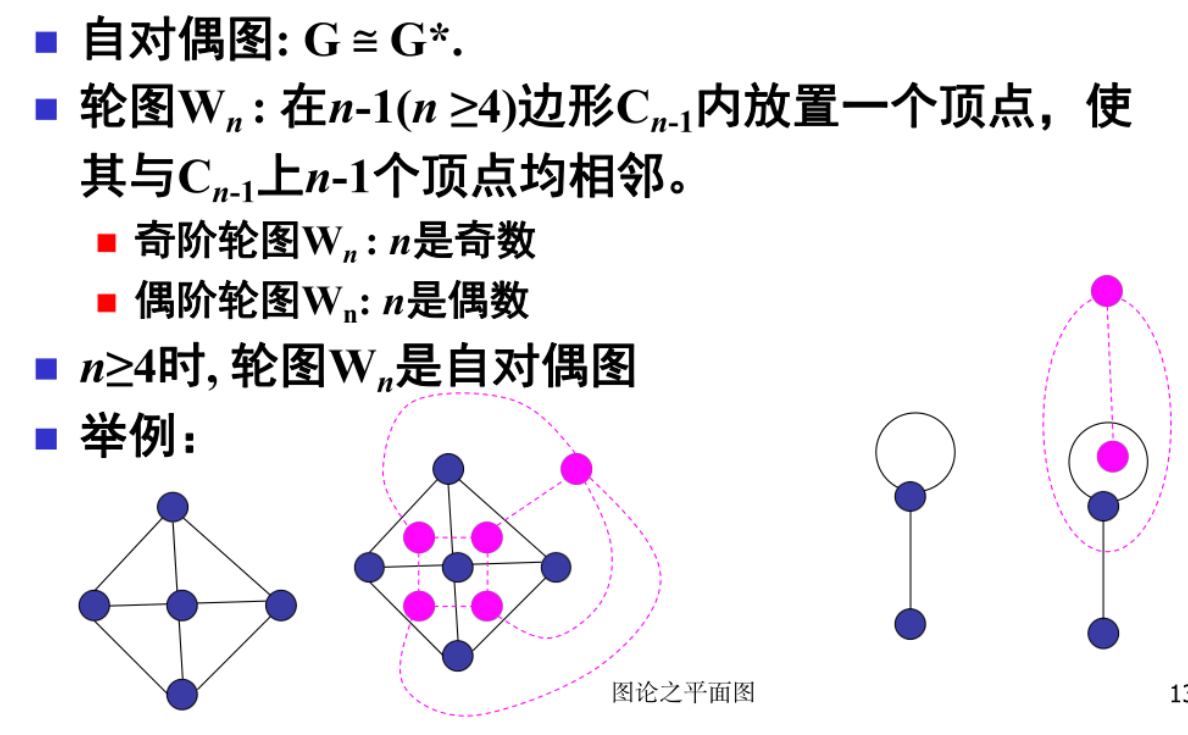
例题

方法1. 利用欧拉定理，且简单图任意面的次数大于等于3

方法2. 上得任意面的次数大于等于3，下证任意面的次数小于等于3。

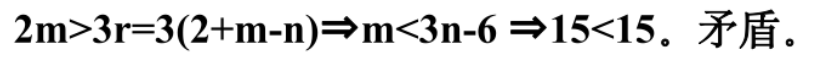
方法3. 利用反证法

第十二章图的着色

能熟练求χ、χ’、χ*（参考PPT）

定义

着色：给图的某类元素（点，边，面）中每个指定一种颜色，使得相邻元素有不同颜色

可k-着色的：能用k中颜色着色（色数小于等于k）

k- 色图：可k着色，但不可(k-1)-着色（色数等于k）

色数：着色所需要最少颜色数

点色数χ(G)，边色数χ'(G)，面色数χ*(G)

理解并记住几个特殊图的χ，χ‘（参考PPT）

点色数

零图的点色数：0

Kn的点色数：n

二部图的点色数：2

推论：G可二着色<=>G是二部图<=>G无奇圈

圈的点色数：2（偶圈），3（奇圈）

轮图的点色数：3（外部为偶圈），4（外部为奇圈）

掌握五色定理的证明方法、即定理12.15和定理12.16及其证明方法

定理12.15：任何平面图都可6-着色

定理12.16(五色定理)：任何平面图都可5-着色

掌握Brooks定理、Vizing定理

定理12.5

条件对于任意图可用，得到的是可n色图

\[\chi(G) \le \Delta(G)+1 \]

定理12.6（Brooks）

图必须是非完全图，非奇圈。同样得到的是可n色图

\[若G连通，非完全图K_n(n\ge3)\bold{非奇圈}，则\chi(G)\le\Delta(G) \]

定理12.17（Vizing）

找到边色数的范围。注意特殊的几个图，可以直接得出边色数

\[\Delta(G)\le\chi^{'}(G)\le\Delta(G)+1 \]

圈的边色数：奇圈为3，偶圈为2

G的面色数和G的对偶图G*边色数的关系

定理12.13：地图（无桥平面图）可k-面着色 <=> 对偶图G*可k-着色

定理12.14：连通无环平面图G可k-面着色 <=>对偶图G*可k-着色（点面互换）

掌握求色数多项式的两种方法（定理12.9和定理12.10）

两个k-着色不同，是指两个k-着色中至少有一个顶点颜色不同

f( G,k )=G的不同k-着色方式的总数，是n次多项式（色多项式）

χ(G) = min{ k | f(G , k) > 0}

特殊图的色多项式

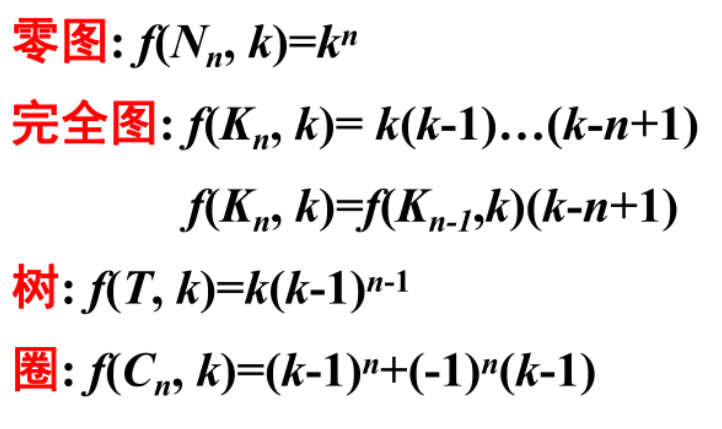
色多项式递推公式（定理12.9）

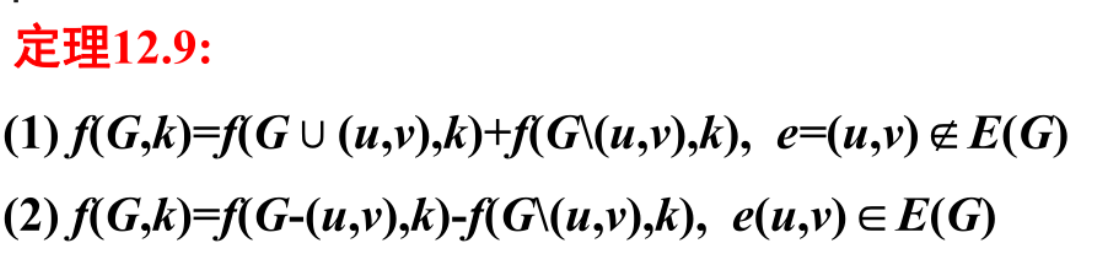
原图加边+收边

原图删边-收边

定理12.10

背下特殊图的色多项式

图的点着色和边着色的应用。例12.4，例12.7

建模。每门课是一个点，有人同时选则这两门课连边。得到图

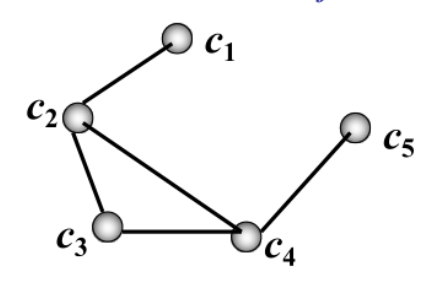
给G进行k-着色。同色点代表可以同一天考的课程，颜色书就是天数。最少天数就是G的色数。则求出色多项式带入色数即可

例12.7

建模。构建二部图，T为教师，C为课。边为ti给cj上一节课。给G进行边着色，同色边代表教学可以同时进行。所以颜色数就是节数，同色边数就是教室数

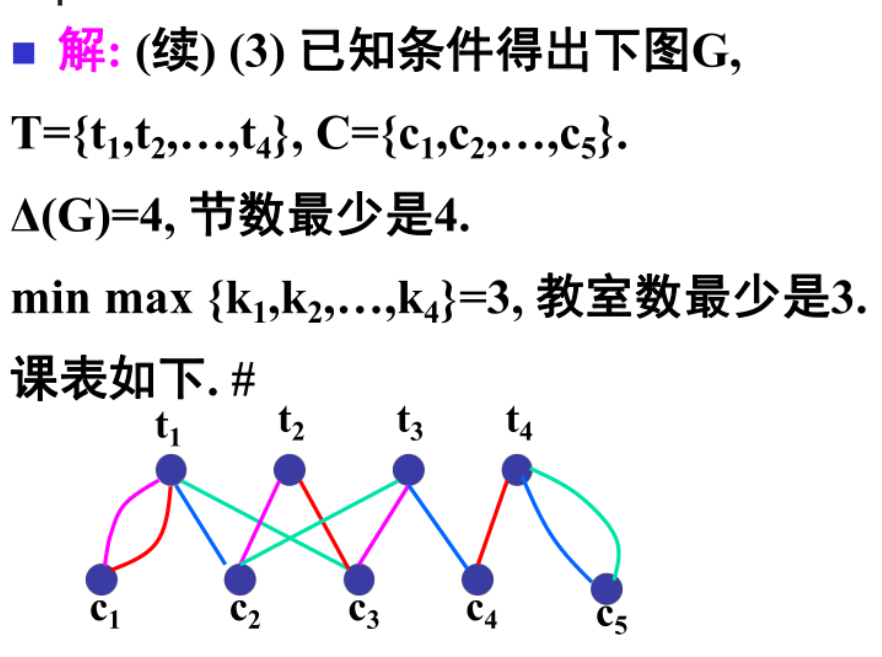
课后例题

1 5 6 7 14

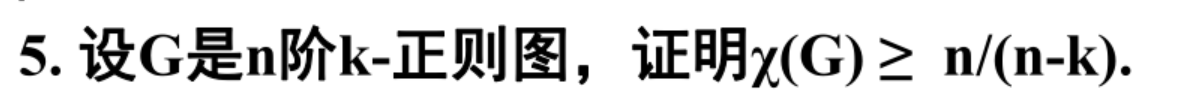
第十三章支配集、覆盖集、独立集与匹配集

掌握极小支配集、极小覆盖集、极大独立集、极大团的概念，并能熟练求出γ0，α0，α1，β0，β1，v0，掌握它们之间的关系

点支配集：即 V 中的顶点要么是 V集合中的元素、要么与 V中的一个顶点相邻。即这些点集可以经过一条边到达其他所有点

极小支配集：去掉一个任何一个点都会使得存在一个点不能直接到达

支配集实例：若干个城镇之间有一个通信网络，要在这些城镇中选定几个建立中心台站，中心台站需与每个城镇都有直通线路，且中心台站数量尽量少。则最少台站数目就是支配数γ0

点覆盖集：点“覆盖”边，（点直接连接某个边）通俗地讲，所谓点覆盖集 V* ，就是 G 中所有的边至少有一个顶点属于 V * 。点所连接的边包含了图所有的边

极小点覆盖：去掉任何一个点都会导致有边是独立的

点覆盖实例：现要在交通网中选择若干交叉路口处建立监控设备，要求能控制所有的道路，且所用的设备尽可能少。最少设备数目就是点覆盖数α0

点独立集：点集的子集中任何两个定点均不直接相邻。即点着色问题中能着同色的点

极大独立集：增加任何一个点都会使得两点相邻

团：一个图中能找到k几

极大团

定理1：设无向图 G(V, E)中无孤立顶点，则 G 的极大点独立集都是 G 的极小支配集。逆命题不成立（即，极小支配集未必是极大独立集）

定理2：一个独立集是极大独立集，当且仅当它是一个支配集。

定理3：设无向图 G(V, E)中无孤立顶点，顶点集合 V * ⊆V，则 V 是 G 的点覆盖，当且仅当* *V–V **是 G 的点独立集。

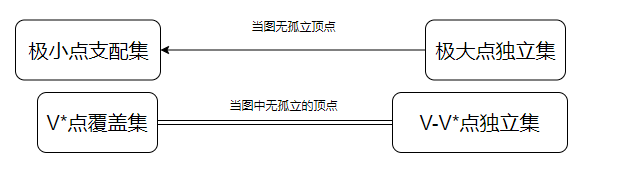
推论：设 G 是 n 阶无孤立点的图，则 V*是 G 的极小（最小）点覆盖集，当且仅当 V–V*是 G 的极大（最大）点独立集，从而有：α0 ＋β0 ＝ n （n 为顶点个数）。

各个名词和符号

掌握最大匹配、完美匹配的定义

匹配：边独立集合

极大匹配：E*是匹配，其真母集都不是

最大匹配：极大匹配中边数最多的匹配

匹配数：β1，最大匹配中边的数量

完美匹配：没有非饱和点（v不与匹配中边关联）的匹配

掌握最大匹配的充分必要条件（定理13.9)

定理13.9

M是G中最大匹配 <=> G中无M可增广路径

掌握完美匹配的充分必要条件（定理13.10）

定理13.10（Tutte）

p奇是奇数阶连通分支

掌握完备匹配的充要条件（hall条件定理13.11，t条件13.12），Hall条件的应用

完备匹配：|M| = |V1| （|V1|≤|V2|）。即少的点都能有边连，且目标不重复

Hall条件：

t条件：上部分点度数有下界，下部分点度数有上界。要求上界≤下界（下方顶点的最大度≤上方顶点的最小度）

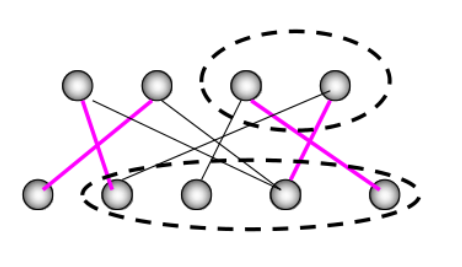
定理13.11（Hall）

二部图G有完备匹配<=>G满足Hall条件（|S|≤|N(S)|）

定理13.12（t）

设G=<V1,V2,E>是二部图，若V1中每个顶点至少关联t（t≥1）条边，而V2中每个顶点至多关联t条边，则G中存在完备匹配

定理13.13

G=<V1,V2,E>是k正则二部图，则G中存在k个边不重的完美匹配